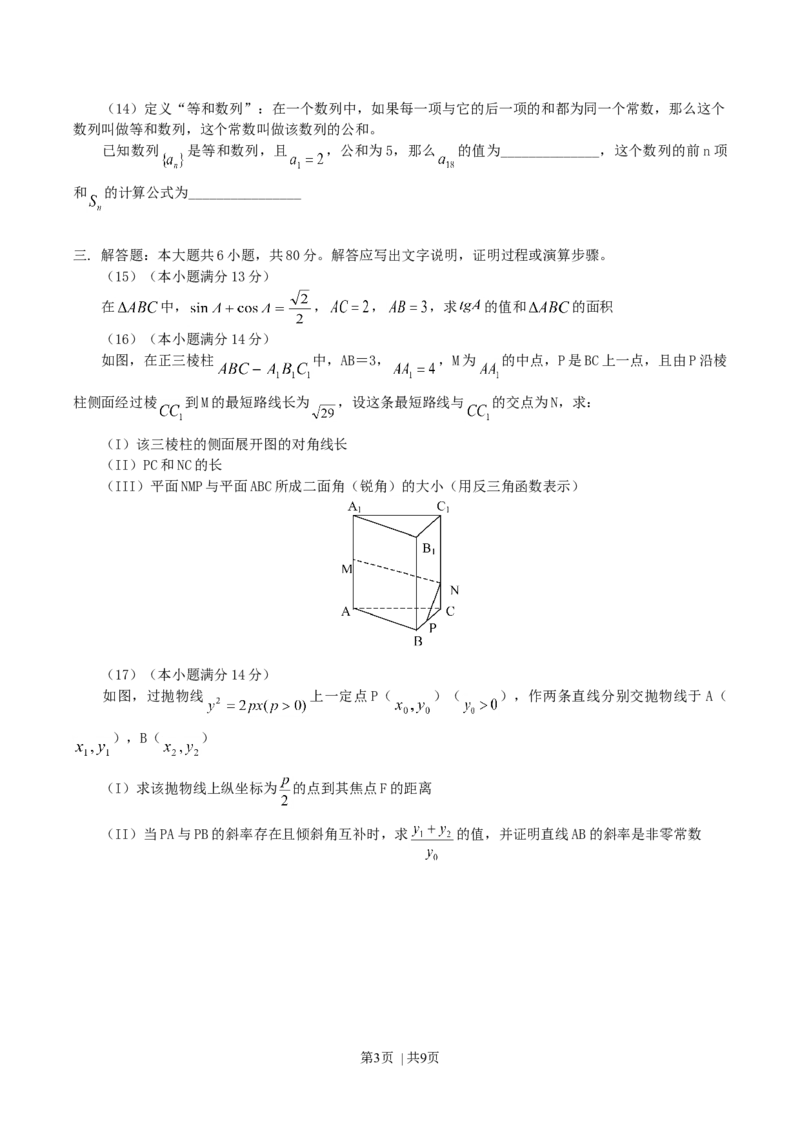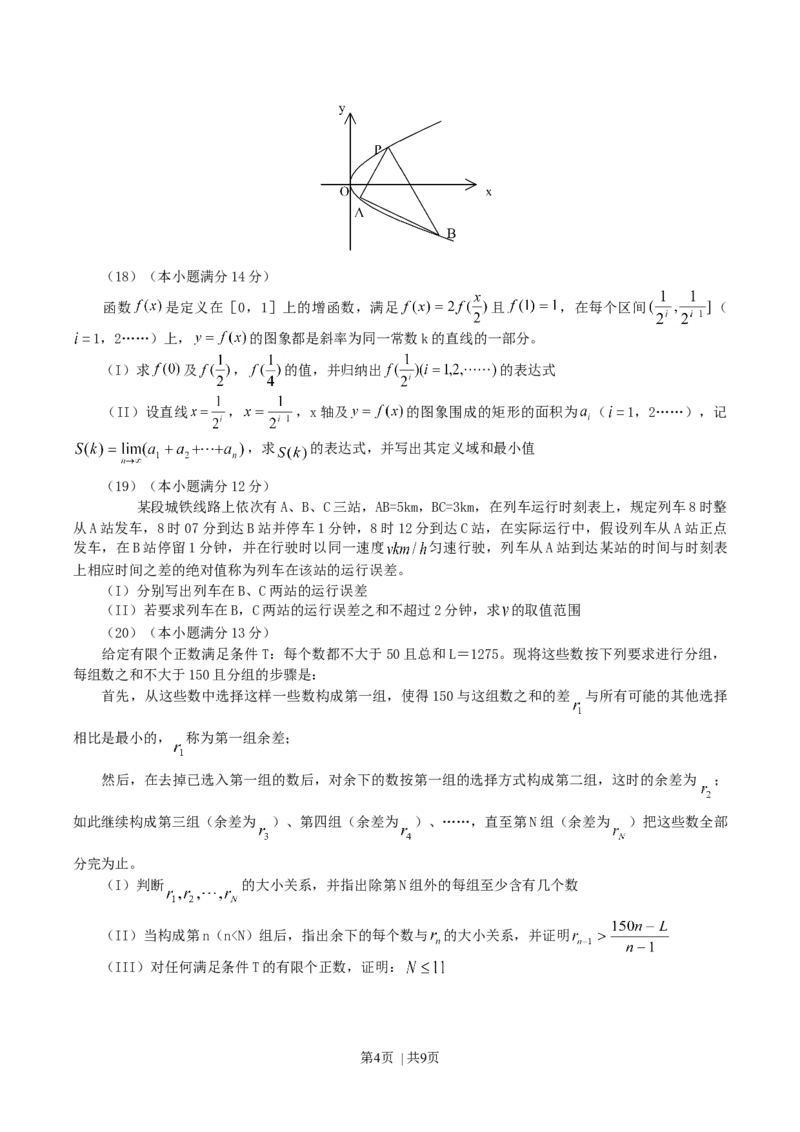文档内容
2004 年北京高考理科数学真题及答案
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。第I卷1至2页。第II卷3至9页。共
150分。考试时间120分钟。
第I卷(选择题 共40分)
注意事项:
1. 答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再
选涂其他答案,不能答在试题卷上。
3. 考试结束,监考人将本试卷和答题卡一并收回。
参考公式:
三角函数的积化和差公式
正棱台、圆台的侧面积公式
其中c’,c分别表示上、下底面周长, 表示斜高或母线长
球体的表面积公式
其中R表示球的半径
一. 选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目
要求的。
(1)设全集是实数集R, , ,则 等于
A. B.
C. D.
(2)满足条件 的复数z在复平面上对应点的轨迹是
A. 一条直线 B. 两条直线 C. 圆 D. 椭圆
(3)设m、n是两条不同的直线, 是三个不同的平面,给出下列四个命题:
①若 , ,则
②若 , , ,则
③若 , ,则
④若 , ,则
其中正确命题的序号是
A. ①和② B. ②和③ C. ③和④ D. ①和④
第1页 | 共9页(4)如图,在正方体 中,P是侧面 内一动点,若P到直线BC与直线
的距离相等,则动点P的轨迹所在的曲线是
A. 直线 B. 圆 C. 双曲线 D. 抛物线
(5)函数 在区间[1,2]上存在反函数的充分必要条件是
A. B. C. D.
(6)已知a、b、c满足 ,且 ,那么下列选项中一定成立的是
A. B. C. D.
(7)从长度分别为1,2,3,4,5的五条线段中,任取三条的不同取法共有n种。在这些取法中,以
取出的三条线段为边可组成的钝角三角形的个数为m,则 等于
A. B. C. D.
( 8 ) 函 数 , 其 中 P 、 M 为 实 数 集 R 的 两 个 非 空 子 集 , 又 规 定
, ,给出下列四个判断:
①若 ,则
②若 ,则
③若 ,则
④若 ,则
其中正确判断有
A. 1个 B. 2个 C. 3个 D. 4个
第II卷(非选择题 共110分)
二. 填空题:本大题共6小题,每小题5分,共30分。把答案填在题中横线上。
(9)函数 的最小正周期是___________
(10)方程 的解是___________________
(11)某地球仪上北纬 纬线的长度为 ,该地球仪的半径是__________cm,表面积是
______________cm2
(12)曲线 C: ( 为参数)的普通方程是__________,如果曲线 C 与直线
有公共点,那么实数a的取值范围是_______________--
(13)在函数 中,若 a,b,c 成等比数列且 ,则 有最
______________值(填“大”或“小”),且该值为______________
第2页 | 共9页(14)定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个
数列叫做等和数列,这个常数叫做该数列的公和。
已知数列 是等和数列,且 ,公和为5,那么 的值为______________,这个数列的前n项
和 的计算公式为________________
三. 解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
(15)(本小题满分13分)
在 中, , , ,求 的值和 的面积
(16)(本小题满分14分)
如图,在正三棱柱 中,AB=3, ,M为 的中点,P是BC上一点,且由P沿棱
柱侧面经过棱 到M的最短路线长为 ,设这条最短路线与 的交点为N,求:
(I)该三棱柱的侧面展开图的对角线长
(II)PC和NC的长
(III)平面NMP与平面ABC所成二面角(锐角)的大小(用反三角函数表示)
(17)(本小题满分14分)
如图,过抛物线 上一定点P( )( ),作两条直线分别交抛物线于A(
),B( )
(I)求该抛物线上纵坐标为 的点到其焦点F的距离
(II)当PA与PB的斜率存在且倾斜角互补时,求 的值,并证明直线AB的斜率是非零常数
第3页 | 共9页(18)(本小题满分14分)
函数 是定义在[0,1]上的增函数,满足 且 ,在每个区间 (
1,2……)上, 的图象都是斜率为同一常数k的直线的一部分。
(I)求 及 , 的值,并归纳出 的表达式
(II)设直线 , ,x轴及 的图象围成的矩形的面积为 ( 1,2……),记
,求 的表达式,并写出其定义域和最小值
(19)(本小题满分12分)
某段城铁线路上依次有A、B、C三站,AB=5km,BC=3km,在列车运行时刻表上,规定列车8时整
从A站发车,8时07分到达B站并停车1分钟,8时12分到达C站,在实际运行中,假设列车从A站正点
发车,在B站停留1分钟,并在行驶时以同一速度 匀速行驶,列车从A站到达某站的时间与时刻表
上相应时间之差的绝对值称为列车在该站的运行误差。
(I)分别写出列车在B、C两站的运行误差
(II)若要求列车在B,C两站的运行误差之和不超过2分钟,求 的取值范围
(20)(本小题满分13分)
给定有限个正数满足条件T:每个数都不大于50且总和L=1275。现将这些数按下列要求进行分组,
每组数之和不大于150且分组的步骤是:
首先,从这些数中选择这样一些数构成第一组,使得150与这组数之和的差 与所有可能的其他选择
相比是最小的, 称为第一组余差;
然后,在去掉已选入第一组的数后,对余下的数按第一组的选择方式构成第二组,这时的余差为 ;
如此继续构成第三组(余差为 )、第四组(余差为 )、……,直至第N组(余差为 )把这些数全部
分完为止。
(I)判断 的大小关系,并指出除第N组外的每组至少含有几个数
(II)当构成第n(n