文档内容
参考答案
一,选择题
1 2 3 4 5 6 7 8
D A B C A C B D
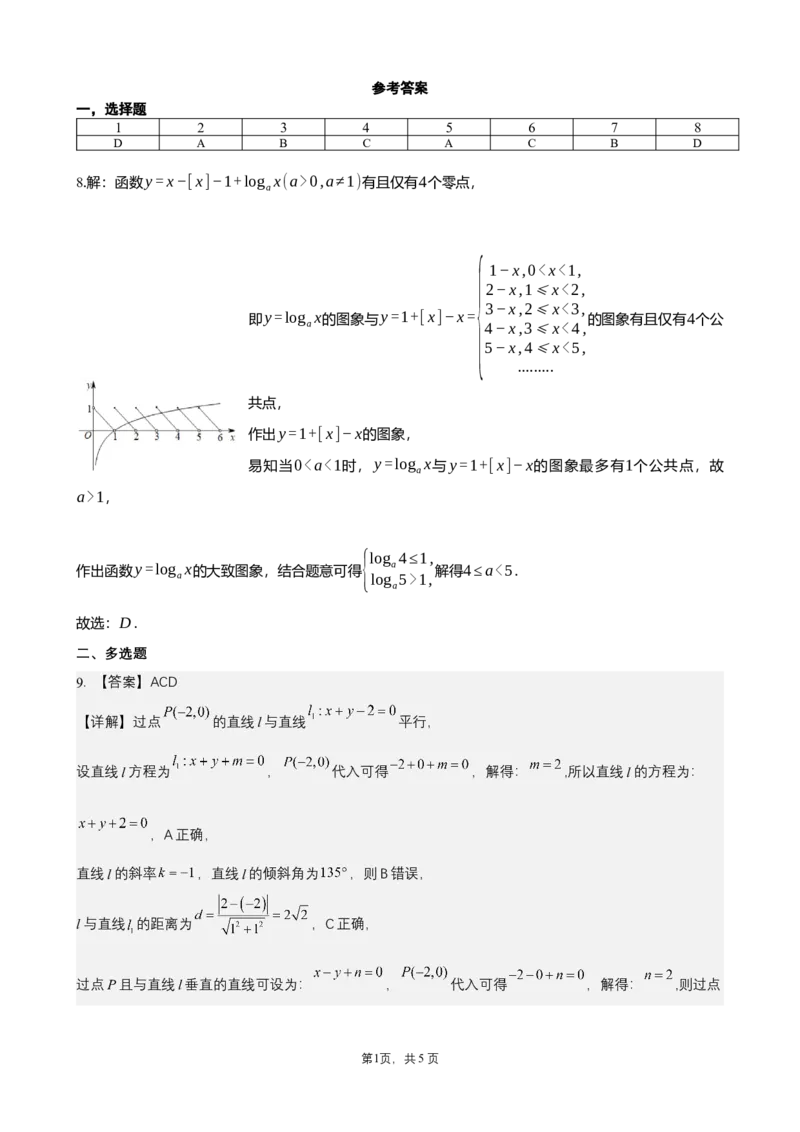
8.解:函数y=x−[x]−1+log x(a>0,a≠1)有且仅有4个零点,
a
1−x,01,
{log 4≤1,
作出函数y=log x的大致图象,结合题意可得 a 解得4≤a<5.
a log 5>1,
a
故选:D.
二、多选题
9. 【答案】ACD
【详解】过点 的直线l与直线 平行,
设直线l方程为 , 代入可得 ,解得: ,所以直线l的方程为:
,A正确,
直线l的斜率 ,直线l的倾斜角为 ,则B错误,
l与直线 的距离为 ,C正确,
过点P且与直线l垂直的直线可设为: , 代入可得 ,解得: ,则过点
第1页,共5页P且与直线l垂直的直线为: ,D正确.
10.【答案】BC 【详解】在正方体 中,由于点 是侧面 的中心,
所以 ,
所以 , ,即 .
11. 【答案】ABD
【详解】显然 ,
当直线 的斜率为0时,直线 与抛物线 只有1个交点,不合要
求,
设直线 为 ,联立 得 ,
,设 ,则 , ,
设 ,则 ,
其中 ,所以 ,
A选项,点 到 轴的最短距离为 ,显然当 时,取得最小值,
故 ,解得 ,A正确;
B选项,由焦半径公式得 , ,
其中 , ,所以 ,
C选项, , ,
第2页,共5页故 , , ,C错误.
D选项,由于 , ,消去 可得 ,
故点 的轨迹方程是 ,D正确;
三、填空题
12. 【答案】2
【详解】 ,则 .
13. 【答案】
【详解】因为圆M与直线. 相切,
所以点 到直线: 的距离即为圆M的半径,
所以 ,圆C的面积为 .
14. 【答案】
【详解】由题设数列的公比为 ,则 ,整理得 ,
当 时,易知 ,符合题意;但当 时, ,
解得 ,且 ,则公比 的取值范围是 .
四、解答题
15. 解:(1)由正弦定理得:sinAcosB+sinBcosA=2sinCcosC,
所以sin(A+B)=2sinCcosC,即sin(π−C)=2sinCcosC,
1 π
因为sinC≠0,所以cosC= ,又C∈(0,π),所以C= ;
2 3
由余弦定理得: ,即 ,
(2) c2=a2+b2−2abcosC 1=a2+b2−ab
1 1 √3 √3 √3
所以1≥2ab−ab,即0