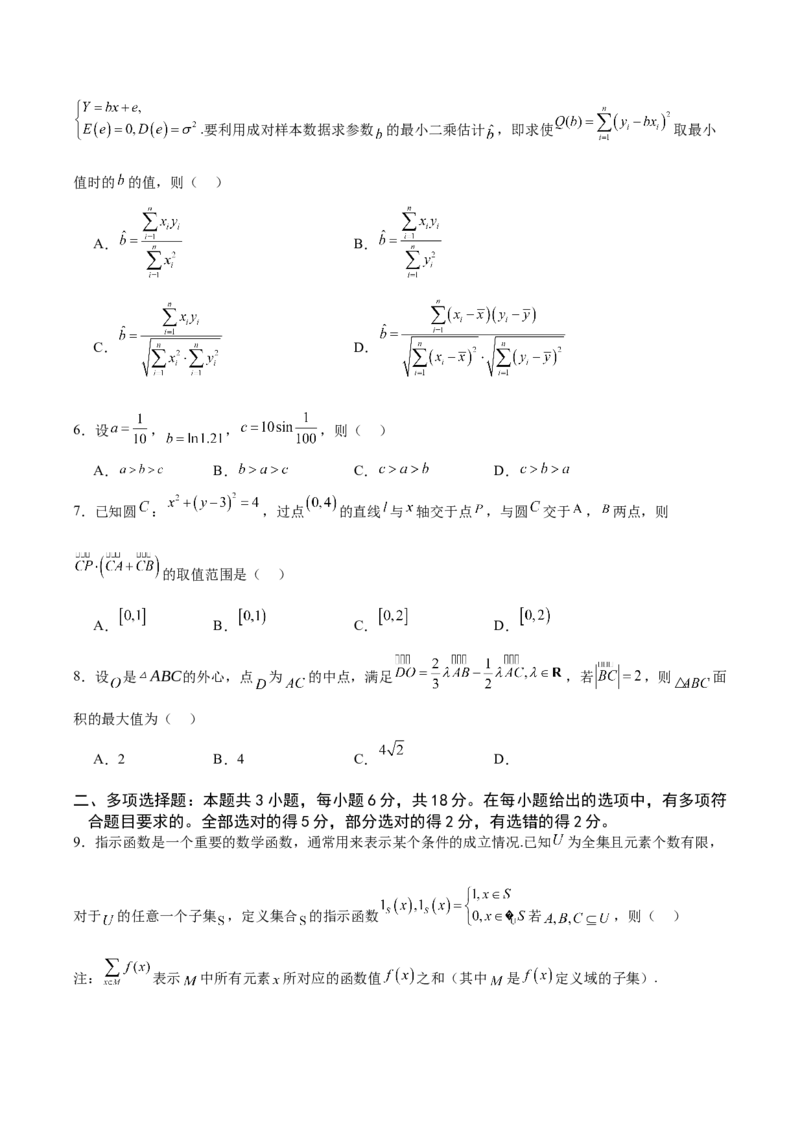文档内容
重庆市乌江新高考协作体 2024 届高考模拟监测(二)
数学试题
(分数:150分,时间:120分钟)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项
是符合题目要求的。
1.“ ,且 ”是“ ,且 ”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.复数 的实部为( )
A.1 B.3 C. D.
3.2024年3月22日国家文物局在北京公布2023年《全国十大考古新发现》,安徽省皖南地区郎溪县磨
盘山遗址成功入选并排名第三,经初步确认,该遗址现存马家浜文化区、崧泽文化区、良渚文化区、钱山漾
文化区四大区域,总面积约6万平方米.该遗址延续时间长、谱系完整,是长江下游地区少有的连续时间近
4000年的中心性聚落.对认识多元化一体中华文明在皖南地区的演进方式具有重要的价值,南京大学历史
学院赵东升教授团队现在对该遗址四大区域进行考古发掘,现安排包含甲、乙在内的6名研究生同学到这4
个区域做考古志愿者,每人去1个区域,每个区域至少安排1个人,则甲、乙两人安排在相同区域的方法
种数为( )
A.96 B.144 C.240 D.360
4.若正四面体 的棱长为 ,M为棱 上的动点,则当三棱锥 的外接球的体积最小
时,三棱锥 的体积为( )
A. B. C. D.
5.假设变量 与变量 的 对观测数据为 ,两个变量满足一元线性回归模型.要利用成对样本数据求参数 的最小二乘估计 ,即求使 取最小
值时的 的值,则( )
A. B.
C. D.
6.设 , , ,则( )
A. B. C. D.
7.已知圆 : ,过点 的直线 与 轴交于点 ,与圆 交于 , 两点,则
的取值范围是( )
A. B. C. D.
8.设 是△ABC的外心,点 为 的中点,满足 ,若 ,则 面
积的最大值为( )
A.2 B.4 C. D.
二、多项选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符
合题目要求的。全部选对的得5分,部分选对的得2分,有选错的得2分。
9.指示函数是一个重要的数学函数,通常用来表示某个条件的成立情况.已知 为全集且元素个数有限,
对于 的任意一个子集 ,定义集合 的指示函数 若 ,则( )
注: 表示 中所有元素 所对应的函数值 之和(其中 是 定义域的子集).A.
B.
C.
D.
10.已知圆 ,圆 ,则( )
A.两圆的圆心距 的最小值为1
B.若圆 与圆 相切,则
C.若圆 与圆 恰有两条公切线,则
D.若圆 与圆 相交,则公共弦长的最大值为2
11.已知集合 ,集合 ,若 有且仅有3个不同元
素,则实数 的值可以为( )
A.0 B.1 C.2 D.3
三、填空题:本题共3小题,每小题5分,共15分。
12.在四边形 中, ,点 是四边形 所在平面上一点,满足
.设 分别为四边形 与 的面积,则 .
13.若关于 的方程 有解,则实数m的最大值为 .
14.四棱锥 的底面 为正方形, 平面 ,且 , .四棱锥
的各个顶点均在球O的表面上, , ,则直线l与平面 所成夹角的范围为
.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15.已知函数 .(1)求曲线 在点 处的切线方程;
(2)当 时, ,求a的取值范围.
16.在△ABC中,内角 所对的边分别为 ,且 .
(1)求角 ;
(2)射线 绕 点旋转 交线段 于点 ,且 ,求 的面积的最小值.
17.某汽车厂商生产某型号具有自动驾驶功能的汽车,该型号汽车配备两个相互独立的自动驾驶系统(记
为系统 和系统 ),该型号汽车启动自动驾驶功能后,先启动这两个自动驾驶系统中的一个,若一个出
现故障则自动切换到另一个系统.为了确定先启动哪一个系统,进行如下试验:每一轮对系统 和 分别
进行测试试验,一轮的测试结果得出后,再安排下一轮试验.当一个系统出现故障的次数比另一个系统少2
次时,就停止试验,并认为出现故障少的系统比另一个系统更稳定.为了方便描述问题,约定:对于每轮
试验,若系统 不出现故障且系统 出现故障,则系统 得1分,系统 得-1分;若系统 出现故障且系
统 不出现故障,则系统 得-1分,系统 得1分;若两个系统都不出现故障或都出现故障,则两个系统
均得0分.系统 出现故障的概率分别记为 和 ,一轮试验中系统 的得分为 分.
(1)求 的分布列;
(2)若系统 和 在试验开始时都赋予2分, 表示“系统 的累计得分为 时,最终认为系
统 比系统 更稳定”的概率,则 , ,其中
.现根据 的值来决定该型号汽车启动自动驾驶功能后先启动哪个系统,若 ,则先启动系统 ;若 ,则先启动系统 ;若 ,则随机启动两个
系统中的一个,且先启动系统 的概率为 .
①证明: ;
②若 ,由①可求得 ,求该型号汽车启动自动驾驶功能后无需自动切换到另一个
自动驾驶系统的概率.
18.双曲线 的焦点为 ( 在 下方),虚轴的右端点为 ,过点 且垂直于
轴的直线 交双曲线于点 ( 在第一象限),与直线 交于点 ,记 的周长为 的周
长为 .
(1)若 的一条渐近线为 ,求 的方程;
(2)已知动直线 与 相切于点 ,过点 且与 垂直的直线分别交 轴, 轴于 两点, 为线段
上一点,设 为常数.若 为定值,求 的最大值.
19.人类对地球形状的认识经历了漫长的历程.古人认为宇宙是“天圆地方”的,以后人们又认为地球是
个圆球.17世纪,牛顿等人根据力学原理提出地球是扁球的理论,这一理论直到1739年才为南美和北欧的
弧度测量所证实.其实,之前中国就曾进行了大规模的弧度测量,发现纬度越高,每度子午线弧长越长的
事实,这同地球两极略扁,赤道隆起的理论相符.地球的形状类似于椭球体,椭球体的表面为椭球面,在
空间直角坐标系下,椭球面 ,这说明椭球完全包含在由平面
所围成的长方体内,其中 按其大小,分别称为椭球的长半轴、中半轴和短半轴.某椭球面与坐标面 的截痕是椭圆 .
(1)已知椭圆 在其上一点 处的切线方程为 .过椭圆 的左焦点
作直线 与椭圆 相交于 两点,过点 分别作椭圆的切线,两切线交于点 ,求△ABM面积的最
小值.
(2)我国南北朝时期的伟大科学家祖暅于5世纪末提出了祖暅原理:“幂势既同,则积不容异”.祖暅原理
用现代语言可描述为:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任意平面所截,如果
截得的两个截面的面积总相等,那么这两个几何体的体积相等.当 时,椭球面 围成的椭球是一个
旋转体,类比计算球的体积的方法,运用祖暅原理求该椭球的体积.