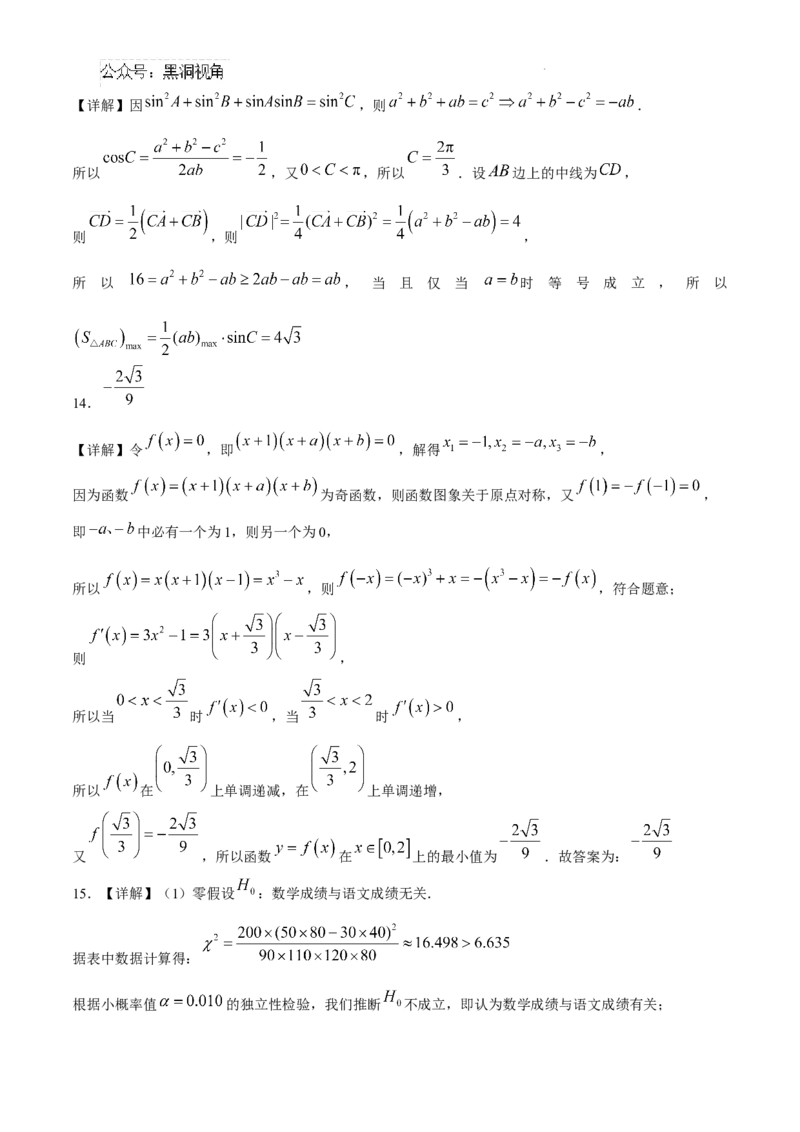文档内容
东莞市2024-2025学年第一学期七校联考试题
一、单项选择题
1.已知集合 , ,则 ( )
A. B. C. D.
2.已知复数 满足 ,则 ( )
A.0 B.1 C. D.2
3.已知 , 满足 , , ,则 , 的夹角为( )
A. B. C. D.
4.已知 , ,则sin(α+β)=( )
A. B. C. D.
5.已知一个圆锥和圆柱的底面半径和高分别相等,若圆锥的轴截面是等边三角形,则这个圆
锥和圆柱的侧面积之比为( )
A. B. C. D.
6.古希腊毕达哥拉斯学派的“三角形数”是一列点(或圆球)在等距的排列下可以形成正三
角形的数,如1,3,6,10,15,…,我国宋元时期数学家朱世杰在《四元玉鉴》中所记载
的“垛积术”,其中的“落一形”锥垛就是每层为“三角形数”的三角锥的锥垛(如图所示,
从上到下,顶上一层1个球,第二层3个球,第三层6个球…),若一“落一形”三角锥垛
有20层,则该锥垛第18层球的个数为( )
A.190 B.171 C.153 D.136
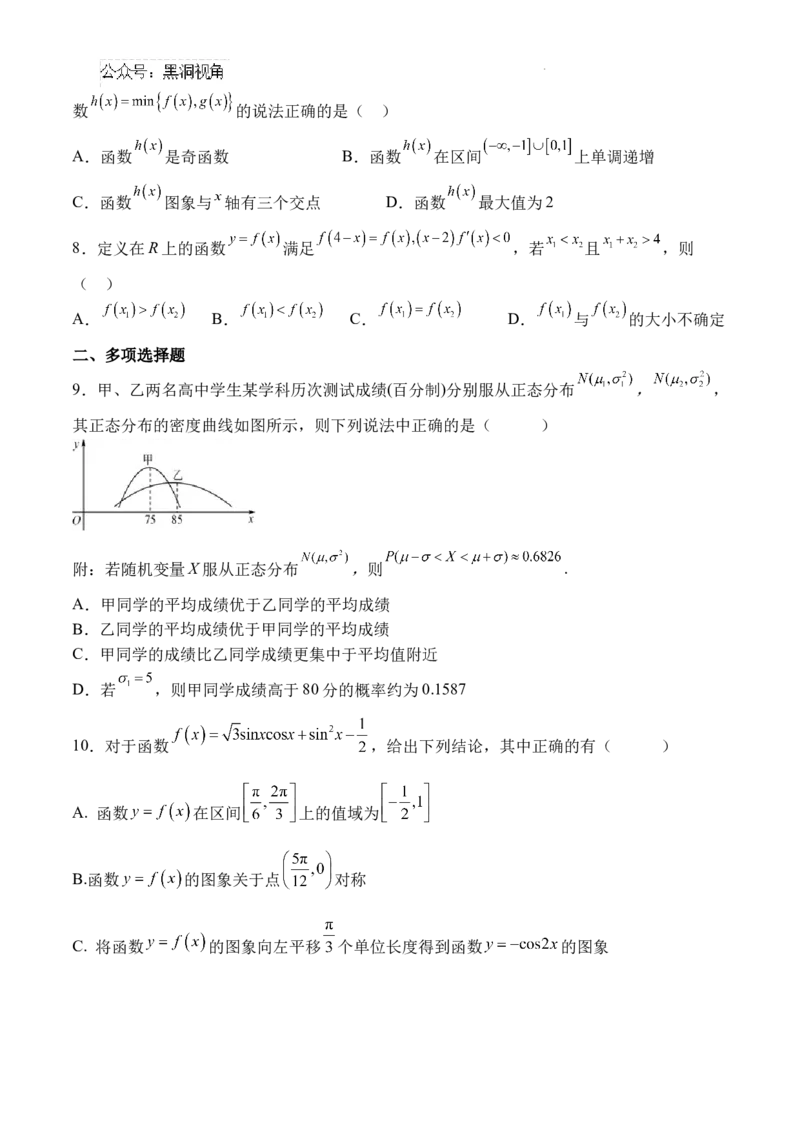
7.对任意两个实数 , ,定义 ,若 , ,则下列关于函
学科网(北京)股份有限公司数 的说法正确的是( )
A.函数 是奇函数 B.函数 在区间 上单调递增
C.函数 图象与 轴有三个交点 D.函数 最大值为2
8.定义在R上的函数 满足 ,若 且 ,则
( )
A. B. C. D. 与 的大小不确定
二、多项选择题
9.甲、乙两名高中学生某学科历次测试成绩(百分制)分别服从正态分布 , ,
其正态分布的密度曲线如图所示,则下列说法中正确的是( )
附:若随机变量X服从正态分布 ,则 .
A.甲同学的平均成绩优于乙同学的平均成绩
B.乙同学的平均成绩优于甲同学的平均成绩
C.甲同学的成绩比乙同学成绩更集中于平均值附近
D.若 ,则甲同学成绩高于80分的概率约为0.1587
10.对于函数 ,给出下列结论,其中正确的有( )
A. 函数 在区间 上的值域为
B.函数 的图象关于点 对称
C. 将函数 的图象向左平移 个单位长度得到函数 的图象
学科网(北京)股份有限公司D. 曲线 在 处的切线的斜率为1
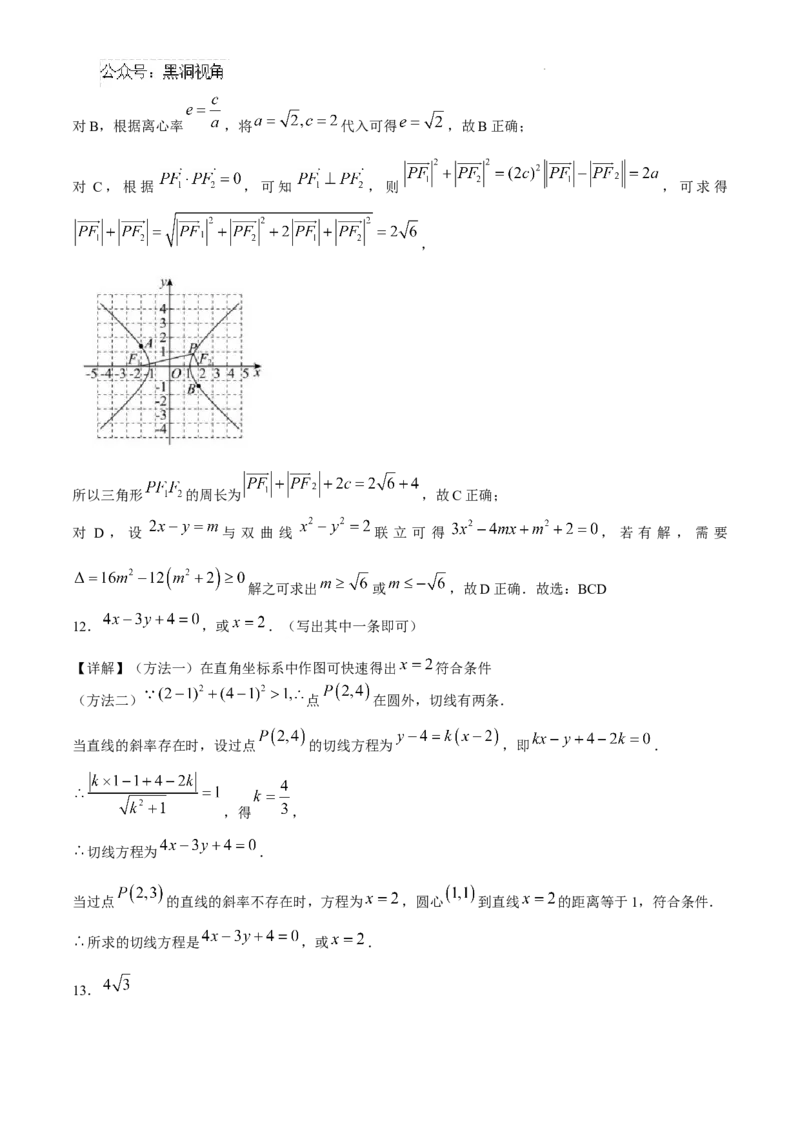
11.已知双曲线C: 的左右焦点分别为 ,且 ,A、P、B为双
曲线上不同的三点,且A、B两点关于原点对称,直线 与 斜率的乘积为1,则下列正确
的是( )
A.双曲线C的实轴长为
B.双曲线C的离心率为
C.若 ,则三角形 的周长为
D. 的取值范围为
三、填空题:本题共3小题,每小题5分,共15分.
12.写出过点 且与圆 相切的一条直线方程:_____________.
13.在 中,若 ,且AB边上的中线长为2,则 面积的
最大值为_______.
14.已知函数 为奇函数,则函数 在 上的最小值为 .
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(本小题满分13分)某数学兴趣小组为研究本校学生数学成绩与语文成绩的关系,采取
有放回的简单随机抽样,从学校抽取样本容量为200的样本,将所得数学成绩与语文成绩的
样本观测数据整理如下:
语文成绩
合计
优
不优秀
秀
优秀 50 30 80
数学
成绩
不优秀 40 80 120
合计 90 110 200
(1)根据小概率值 的独立性检验,能否认为数学成绩与语文成绩有关联?
学科网(北京)股份有限公司(2)在人工智能中常用 表示在事件 发生的条件下事件 发生的优势,在统
计中称为似然比.现从该校学生中任选一人, 表示“选到的学生语文成绩不优秀”, 表示
“选到的学生数学成绩不优秀”.请利用样本数据,估计 的值.
附:
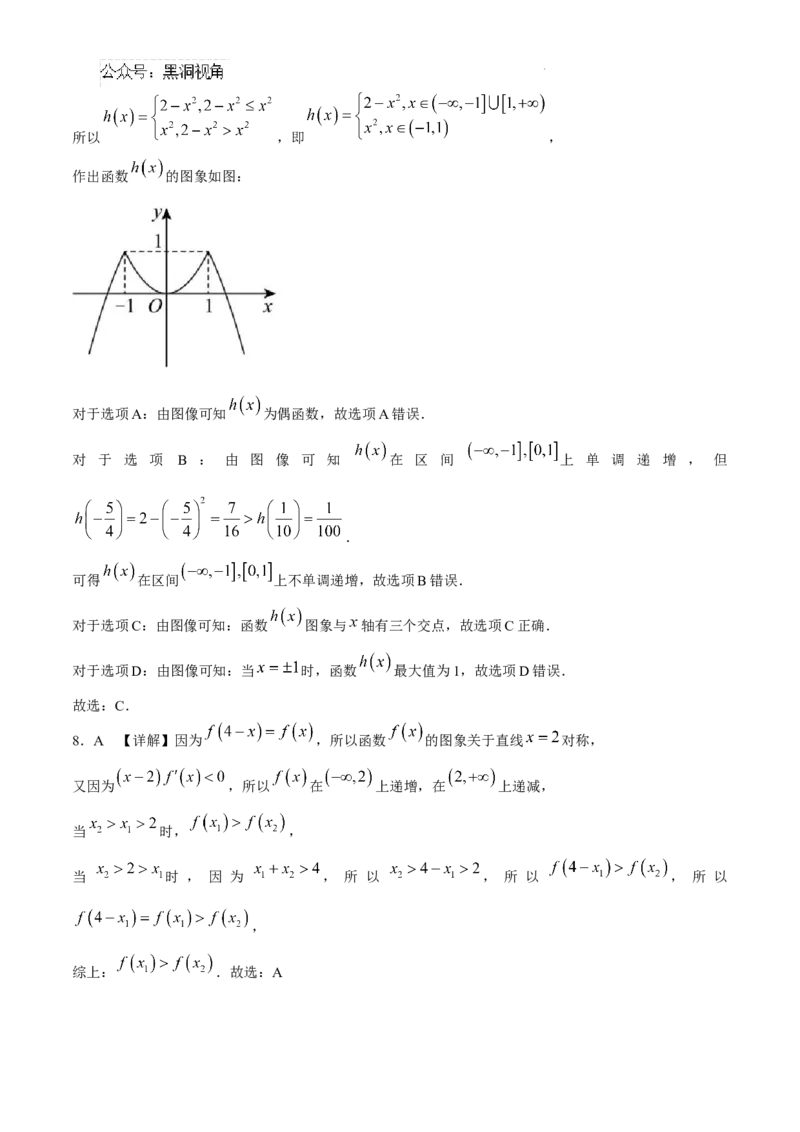
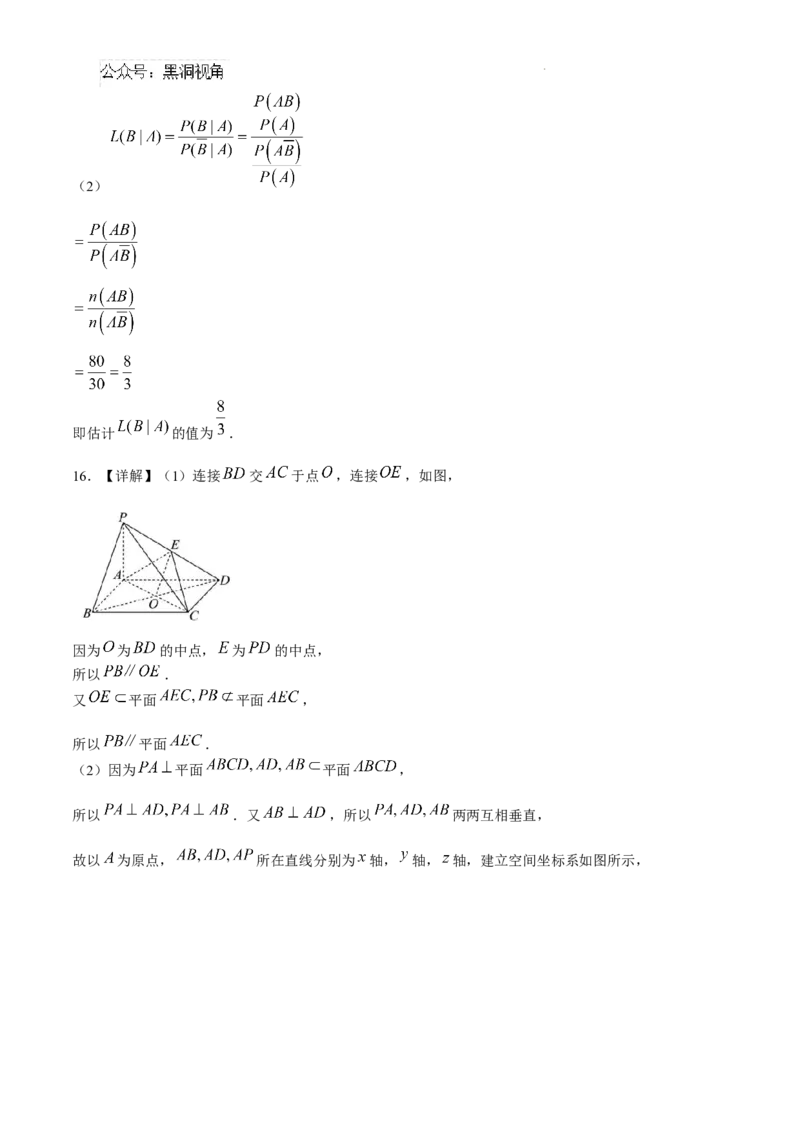
16.(本小题满分15分)如图,在四棱锥 中,底面 为矩形, 平面
为 的中点.
(1)证明: 平面 .
(2)若平面 与平面 的夹角为 ,求 的长.
17.(本小题满分15分)已知数列 的前 项和为 , ,数列 是以1为公差的等
差数列.
(1)求数列 的通项公式;
(2)若对于任意正整数 ,都有 ,求实数 的最小值.
18.(本小题满分17分)已知函数
(1)当 时,求曲线 在点 处的切线方程;
(2)若函数 有两个不同的零点 , .
①求实数a的取值范围;
②证明: .
学科网(北京)股份有限公司19.(本小题满分17分)通过研究,已知对任意平面向量 ,把 绕其起点A沿逆时
针方向旋转 角得到向量 ,叫做把点B绕点A逆时针方向旋转
角得到点P
(1)已知平面内点 ,点 ,把点B绕点A逆时针旋转 得到点P,求点P
的坐标:
(2)已知二次方程 的图象是由平面直角坐标系下某标准椭圆
绕原点O逆时针旋转 所得的斜椭圆C,
(i)求斜椭圆C的离心率;
(ⅱ)过点 作与两坐标轴都不平行的直线 交斜椭圆C于点M、N,过原点O作直
线 与直线 垂直,直线 交斜椭圆C于点G、H,判断 是否为定值,若是,请求
出定值,若不是,请说明理由.
东莞市 2024-2025 学年第一学期七校联考高三数学参考答案
题 1 2 3 4 5 6 7 8 9 10 11
号
答 D A B D C B C A BCD AD BCD
案
1.D 2.A
3.В 【详解】因为 ,所以 ,
学科网(北京)股份有限公司则 ,由于 ,所以 .故选:B
4 . D 【 详 解 】 因 为 , 所 以
, 所 以
,
两式相加可得: ,
所以 所以 ,解得 ,故选:D
5.C 【详解】设圆锥和圆柱的底面半径为 ,
因为圆锥的轴截面是等边三角形,所以圆锥的 母线长为 ,则圆锥和圆柱的高为
,
所以圆锥的侧面积为 ,圆柱的侧面积为 ,
所以圆锥和圆柱的侧面积之比为 ,故选:C.
6 . B 【 详 解 】 由 于 “ 三 角 形 数 ” 可 以 写 为
, 故 第 层 “ 三 角 形 数 ” 为
,则第18层球的个数为171.
7.C 【详解】由题意可得: ,
令 ;解得 或 ;令 ;解得 ;
学科网(北京)股份有限公司所以 ,即 ,
作出函数 的图象如图:
对于选项A:由图像可知 为偶函数,故选项A错误.
对 于 选 项 B : 由 图 像 可 知 在 区 间 上 单 调 递 增 , 但
.
可得 在区间 上不单调递增,故选项B错误.
对于选项C:由图像可知:函数 图象与 轴有三个交点,故选项C正确.
对于选项D:由图像可知:当 时,函数 最大值为1,故选项D错误.
故选:C.
8.A 【详解】因为 ,所以函数 的图象关于直线 对称,
又因为 ,所以 在 上递增,在 上递减,
当 时, ,
当 时 , 因 为 , 所 以 , 所 以 , 所 以
,
综上: .故选:A
学科网(北京)股份有限公司9.BCD【详解】解:由图象可知,甲的图象关于 对称,乙的图象关于 对称,
所以甲同学的平均成绩为75分,乙同学的平均成绩为85分,故选项B正确,A错误;
因为甲的图象比乙的图象更“高瘦”,所以甲的成绩比乙的成绩更集中于平均值左右,
则甲同学成绩的方差比乙同学成绩的方差小,故选项C正确;
若 ,则甲同学成绩高于80分的概率约为 ,故选项D正确.故选:ACD.
10.AD 【详解】由题意知 ,
对于A,因为 ,所以 ,则 ,A正确;
对于B, ,故函数 的图象不关于点 对称,B
错误;
对 于 C , 将 函 数 的 图 象 向 左 平 移 个 单 位 长 度 得 到 函 数
的图象,C错误;
对于D, ,则 ,
故曲线 在 处的切线的斜率为1,D正确,故选:BD
11.【答案】BCD 【详解】根据题意可知 ,所以 ,设 ,则
, 将 分 别 代 入 到 双 曲 线 后 相 减 可 得
代入可求解出 ,
对A,根据 ,解之可得 ,所以双曲线 的实轴长为 ,故A错误;
学科网(北京)股份有限公司对B,根据离心率 ,将 代入可得 ,故B正确;
对 C,根据 ,可知 ,则 ,可求得
,
所以三角形 的周长为 ,故C正确;
对 D , 设 与 双 曲 线 联 立 可 得 , 若 有 解 , 需 要
解之可求出 或 ,故D正确.故选:BCD
12. ,或 .(写出其中一条即可)
【详解】(方法一)在直角坐标系中作图可快速得出 符合条件
(方法二) 点 在圆外,切线有两条.
当直线的斜率存在时,设过点 的切线方程为 ,即 .
,得 ,
切线方程为 .
当过点 的直线的斜率不存在时,方程为 ,圆心 到直线 的距离等于1,符合条件.
所求的切线方程是 ,或 .
13.
学科网(北京)股份有限公司【详解】因 ,则 .
所以 ,又 ,所以 .设 边上的中线为 ,
则 ,则 ,
所 以 , 当 且 仅 当 时 等 号 成 立 , 所 以
14.
【详解】令 ,即 ,解得 ,
因为函数 为奇函数,则函数图象关于原点对称,又 ,
即 中必有一个为1,则另一个为0,
所以 ,则 ,符合题意;
则 ,
所以当 时 ,当 时 ,
所以 在 上单调递减,在 上单调递增,
又 ,所以函数 在 上的最小值为 .故答案为:
15.【详解】(1)零假设 :数学成绩与语文成绩无关.
据表中数据计算得:
根据小概率值 的独立性检验,我们推断 不成立,即认为数学成绩与语文成绩有关;
学科网(北京)股份有限公司(2)
即估计 的值为 .
16.【详解】(1)连接 交 于点 ,连接 ,如图,
因为 为 的中点, 为 的中点,
所以 .
又 平面 平面 ,
所以 平面 .
(2)因为 平面 平面 ,
所以 .又 ,所以 两两互相垂直,
故以 为原点, 所在直线分别为 轴, 轴, 轴,建立空间坐标系如图所示,
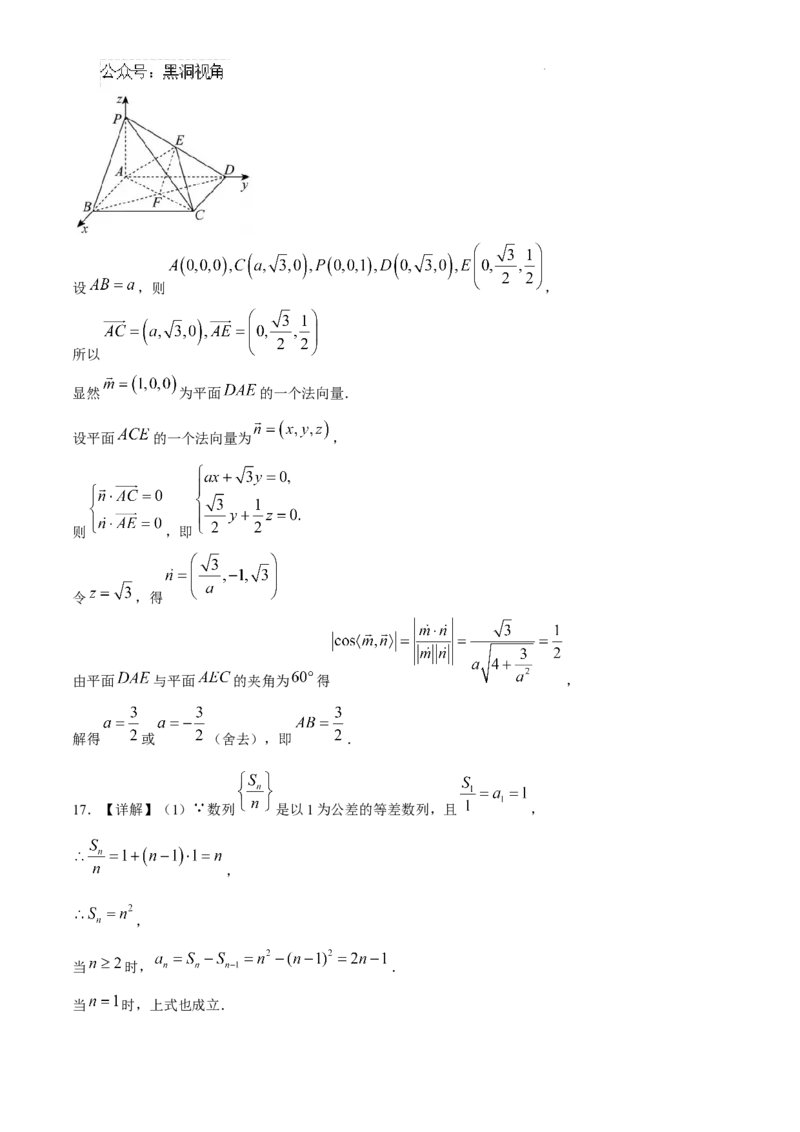
学科网(北京)股份有限公司设 ,则 ,
所以
显然 为平面 的一个法向量.
设平面 的一个法向量为 ,
则 ,即
令 ,得
由平面 与平面 的夹角为 得 ,
解得 或 (舍去),即 .
17.【详解】(1) 数列 是以1为公差的等差数列,且 ,
,
,
当 时, .
当 时,上式也成立.
学科网(北京)股份有限公司(2)由
则
而
所以 ,即 的最小值为
18.【详解】解:(1)当 时, , ,
所以 ,
所以曲线 在点 处的切线方程是
(2)函数 有两个不同的零点 ,
等价于方程 有两个不同实根 ,
①令 ,则 ,
学科网(北京)股份有限公司所以 在 上单调递增,在 上单调递减,
由于 ,当 时, ;当 ,
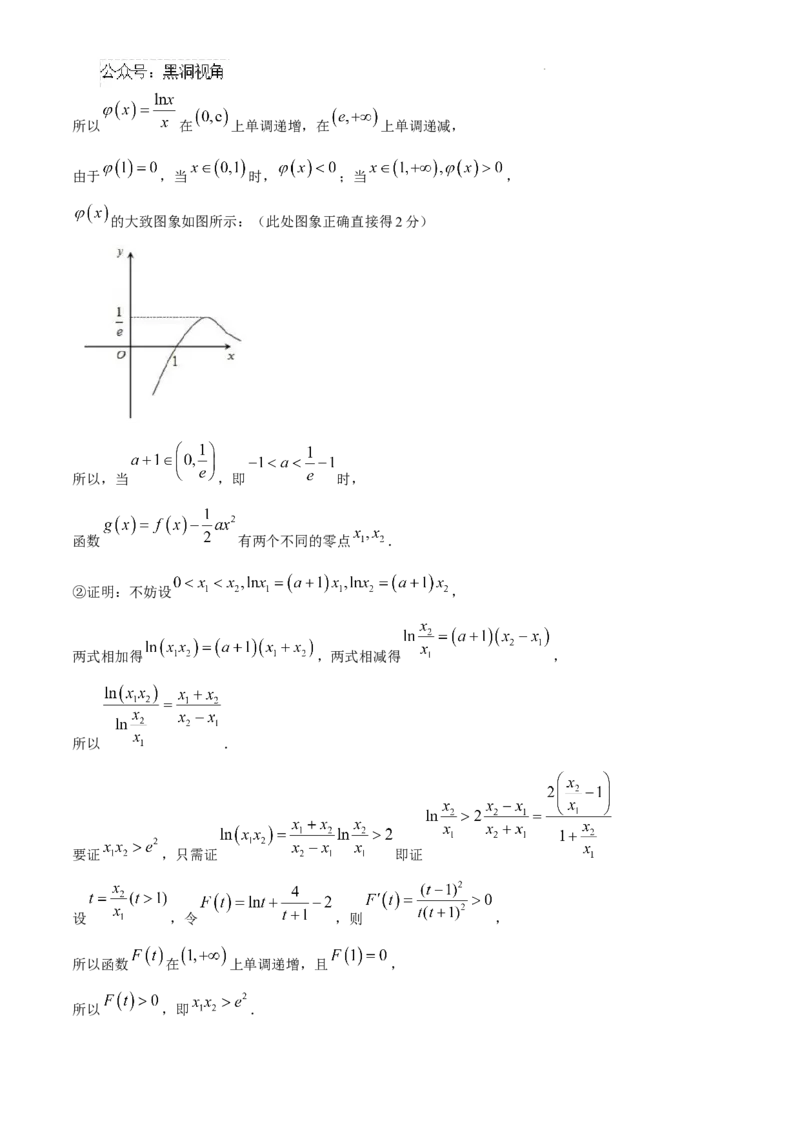
的大致图象如图所示:(此处图象正确直接得2分)
所以,当 ,即 时,
函数 有两个不同的零点 .
②证明:不妨设 ,
两式相加得 ,两式相减得 ,
所以 .
要证 ,只需证 即证
设 ,令 ,则 ,
所以函数 在 上单调递增,且 ,
所以 ,即 .
学科网(北京)股份有限公司19.【详解】(1)由已知可得 ,则 ,
设 ,则 ,
所以 ,即点P的坐标为 ;
(2)①由 与 交点为 和 ,则 ,
由 与 交点为 和 ,则 ,
所以 ;
②法一:设直线
与斜椭圆 联立: ,
有 ,
,
设直线 ,代入斜椭圆 ,
学科网(北京)股份有限公司有 ,
,
故 .
法二:将粗圆顺时针旋转 ,由已知可得椭圆方程为 ,点Q旋转后的坐标为 ,
当直线 旋转后斜率不存在时, ,
当直线 旋转后斜率存在时,设直线 旋转后为 ,旋转后 ,
与椭圆方程 联立,即 ,可得 ,
,
设直线 旋转后为 ,代入粗圆方程 中,
有 ,
.
学科网(北京)股份有限公司综上所述, .
学科网(北京)股份有限公司