重庆市巴蜀中学2024届高考适应性月考卷（六）数学试题_2024年2月_01每日更新_22号_2024届重庆市巴蜀中学高考适应性月考卷(六)_重庆市巴蜀中学2024届高考适应性月考卷(六)数学

巴蜀中学 2024 届高考适应性月考卷（六） 数 学 注意事项: 1.答题前,考生务必用黑色碳素笔将自己的姓名、准考证号、考场号、座位号在答题卡上 填写清楚. 2.每小题选出答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮 擦干净后,再选涂其他答案标号.在试题卷上作答无效. 3.考试结束后,请将本试卷和答题卡一并交回.满分150分,考试用时120分钟. 一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项 是符合题目要求的)  x1  1.已知集合 Ax  0,B  x 0 x 2∣,则 AB  x1  A. 1,2  B. 1,2    C. 0,1   D. 0,2 2.小李同学参加了高三以来进行的6次数学测试,6次成绩依次为:90分、100分、120分、 115分、130分、125分.则这组成绩数据的上四分位数为 A.120 B.122.5 C.125 D.130 3.2023年11月30日,重庆市轨道交通新开通6个站点,包括5号线中段忠恕沱、红岩村、歇 台子3个站点和10号线南湖、万寿路、兰花路3个站点,为广大市民的出行提供了更多便利. 某同学从中随机选择4个站点实地考察周边情况,则在红岩村被选中的条件下,10号线不少于2 个站点的概率为 9 A. 10 7 B. 10 3 C. 5 1 D. 10 2 5 5  4.已知单位圆 x2  y2 1 上一点 A , ,现将点 A 绕圆心逆时针旋转 到点 B,   5 5 6   则点 B 的横坐标为 152 5 A. 10 第 1 页 共 6 页152 5 B. 10 2 15 5 C. 10 2 15 5 D. 10 5.已知正方体 ABCDABC D ,棱 BC,CC 的中点分别为 E,F ,平面 AEF 截正方体得 1 1 1 1 1 V 两个几何体,体积分别记为 V ,V  V V  ,则 1  1 2 1 2 V 2 1 A. 2 5 B. 7 7 C. 13 7 D. 17 6.已知直线 l:xmy10  mR  ,圆 C:x2  y2 2 1,则下列说法正确的是 A. l 表示经过  1,0  的所有直线 B.圆上的点到直线距离的最小值为 51 C.圆上的点到直线距离的最大值为 51 4 D.若直线 l 与圆 C 相切,则 m 3 7.定义:满足 a n2 : a n1 q  q 为常数, nN*  的数列  a  称为二阶等比数列, q 为二阶公 a a n n1 n 比.已知二阶等比数列∣a  的二阶公比为 2,a 1,a  2 ,则使得 a 2024 成立的最 n 1 2 n 小正整数 n 为 A.7 B.8 C.9 D.10 x2 y2 8.已知椭圆  1  ab0  的右焦点为 F ,过点 F 的直线与圆 x2  y2 b2 相切于 a2 b2 点 E 且与椭圆相交于 M,N 两点,若 E,F 恰为线段 MN 的三等分点,则椭圆的离心率为 5 A. 3 3 B. . 5 第 2 页 共 6 页5 C. 4 2 D. 5 二、多项选择题(本大题共3个小题,每小题6分,共18分,在每个给出的四个选项中,有多项符 合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分) 9.已知复数 z 的共轭复数为 z ,则下列命题正确的是 A. zzR B. zz 为纯虚数 C. z  z 2 D. z  z2 10.定义在 R 上的函数 f  x  满足 f  x  f  y 2f  xy 0,且 f  x  不是常值函数(即: f  x 的值域不是单元素集合)，则 A. f  1 2 B. f  0 0 C. x0 时, f  x 0 D. f  x  为奇函数 11.已知正六棱雉 P ABCDEF 的底面边长为2,体积为 4 3,过 AB 的平面 与 PC,PF 分别交于点 M,N.则下列说法正确的有 A. P ABCDEF 的外接球的表面积为 16 B. AB//MN C. BE CN D.从点 A 沿正六棱雉侧面到点 D 的最短路径长为5 三、填空题（本大题共3小题,每小题5分,共15分)     12.已知 x0,y0,向量 a  x,y  ,b  2,1  ,ab 1,则 xy 的最大值为 . 13.已知斜率为2的直线经过抛物线 C:x2 4y 的焦点 F ,交抛物线于 A,B 两点,则 AB  ________.   14.已知函数 f  x 2 3sinxcosx2cos2x(0) 的定义域为   0, 2   .若存在唯一 x 0 , 使得 f  x  f  x  佰成立,则正实数的取值范围是_________. 0 四、解答题 (共77分, 解答应写出文字说明, 证明过程或演算步骤) 15.(本小题满分13分) 已知数列  a∣满足: a 3 且 a 2a 2n1. n 1 n1 n 第 3 页 共 6 页(1)判断数列 a 2n1 是否为等比数列,并求出 a 的通项公式; n n (2)将数列 a 中满足不等式 2k a 2k1  kN*  的项数记为 b ,求数列 b 的前 k 项 n n k k 和 S . 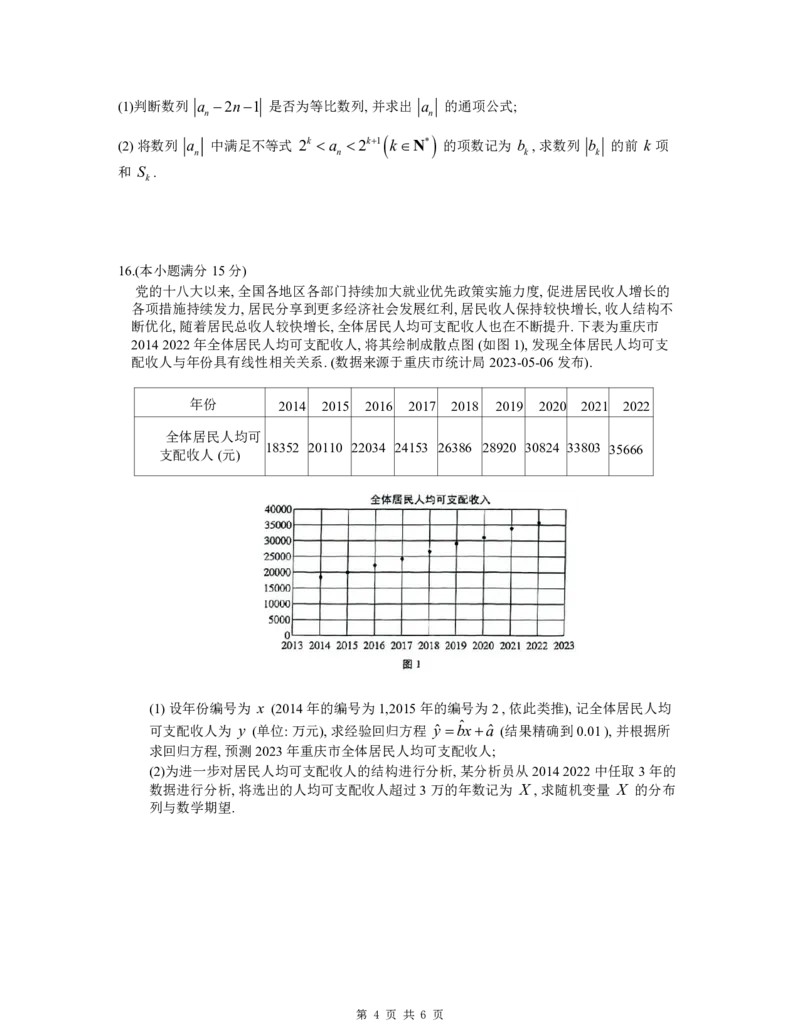k 16.(本小题满分15分) 党的十八大以来,全国各地区各部门持续加大就业优先政策实施力度,促进居民收人增长的 各项措施持续发力,居民分享到更多经济社会发展红利,居民收人保持较快增长,收人结构不 断优化,随着居民总收人较快增长,全体居民人均可支配收人也在不断提升.下表为重庆市 20142022年全体居民人均可支配收人,将其绘制成散点图(如图1),发现全体居民人均可支 配收人与年份具有线性相关关系.(数据来源于重庆市统计局2023-05-06发布). 年份 2014 2015 2016 2017 2018 2019 2020 2021 2022 全体居民人均可 支配收人(元) 18352 20110 22034 24153 26386 28920 30824 33803 35666 (1)设年份编号为 x (2014年的编号为1,2015年的编号为2,依此类推),记全体居民人均 可支配收人为 y (单位:万元),求经验回归方程 yˆ b ˆ xaˆ (结果精确到0.01),并根据所 求回归方程,预测2023年重庆市全体居民人均可支配收人; (2)为进一步对居民人均可支配收人的结构进行分析,某分析员从20142022中任取3年的 数据进行分析,将选出的人均可支配收人超过3万的年数记为 X ,求随机变量 X 的分布 列与数学期望. 第 4 页 共 6 页9 9 参考数据: y 24.03,x y 133.39. i i i i1 i1 参考公式:对于一组数据  u ,v  ,  u ,v  ,,  u ,v  ,其回归直线方程 vˆ ˆ uˆ 的斜率和 1 1 2 2 n n n  u u  v v  截距的最小二乘估计分别为 ˆ  i1 i i ,ˆ  vˆ u . n  u u 2 i1 i 17.(本小题满分15分) 如图2,在正四棱台 ABCDABC D 中, AB 2AB 4. 1 1 1 1 1 1 (1)求证:平面 ABCD 平面 ACC A ; 1 1 3 (2)若直线 BC 与平面 ACC A 所成角的正切值为 ,求二面角 BCC A 的正弦值. 1 1 1 6 1 18.(本小题满分17分) 1 已知 C 2,0  ,C  2,0  ,动点 P 满足 PC 与 PC 的斜率之积为定值 . 1 2 1 2 4 (1)求动点 P 的轨迹  的方程; (2)过点 M  4,0  的直线 l 与曲线  交于 A;B 两点,且 A,B 均在 y 轴右侧,过点 A 作直 线 l:x1 的垂线,垂足为 D. (i)求证:直线 BD 过定点; (ii)求 MBD 面积的最小值. 第 5 页 共 6 页19.(本小题满分17分) 对于函数 y  f  x  ,xI ,若存在 x I,使得 f  x  x ,则称 x 为函数 f  x  的一阶不 0 0 0 0 动点;若存在 x I,使得 f  f  x   x ,则称 x 为函数 f  x  的二阶不动点;依此类推,可 0 0 0 0 以定义函数 f  x  的 n 阶不动点.其中一阶不动点简称不动点,二阶不动点也称为稳定点. (1)已知 f  x 2x 2x3,求 f  x  的不动点; (2)已知函数 f  x  在定义域内单调递增,求证:“ x 为函数 f  x  的不动点”是“ x 为函数 0 0 f  x  的稳定点”的充分必要条件; 2 1 (3)已知 a 1,讨论函数 f  x  lnx a1  x 的稳定点个数. e2 x 第 6 页 共 6 页