文档内容
德阳市高中 2024 级高二上期期中教学质量监测考试
数学
参考答案及评分标准
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选
项中,只有一项是符合题目要求的)
1-4:DCBC 5-8:ABBD
二、多项选择题(本题共3小题,每小题6分,共18分.在每小题给出的四个选项
中,有几项是符合题目要求的)
9. ABC 10.BCD 11.ABC
三、填空题(本题共3小题,每小题5分,共15分)
5
12. 0(或0°) 13. 14. 18
6
四、填空题(共77分)
y−2 x−0
15.解(1)由两点式得边AB所在直线方程为 = ,即x+ y−2=0...........4
3−2 −1−0
分
2−0 1
( 2 ) 因 为 k = = , AC 的 中 点 D(−2,1)
AC 0−(−4) 2
,.................................................................7分
所以AC边上的垂直平分线所在直线方程为y−1=−2(x+2),即2x+ y+3=0.....9分
|−4+0−2|
( 3 ) 点 C 到 边 AB 的 距 离 为 d= =3√2, |AB|=√2
√2
,......................11分
1 1
S = ×|AB|×d= ×√2×3√2=3......................................13分
∆ABC 2 2
16.解(1)∵ 为线段 的中点,∴ ,
∵ ,∴ ,.............................................2分
∴⃗PM=⃗PA+⃗AM.....................................4分
............................................6分
;..............................................7分
(2) ...................................9分
..............11分
1 1 1 1
=−8×6× + ×6×6× + ×62 ..................................................................13分
2 3 2 6
=−24+6+6=−12..............................................15分
17.解(1)记甲,乙,丙三人在计算机三级上机考试中合格依次为事件A ,B ,C
1 1 1
在笔试考试中合格依次为A ,B ,C ....................................................................................2分
2 2 2
设甲没有获得执业医师证书的概率为P
...............................................6分
(2)甲、乙、丙获得计算机三级证书依次为A A ,B B ,C C
1 2 1 2 1 2
并且A 与A ,B 与B ,C 与C 相互独立........................................8
1 2 1 2 1 2
分
4 1 2 3 2 1 2 2 4
则 P(A A )= × = , P(B B )= × = , P(C C )= × =
1 2 5 2 5 1 2 4 3 2 1 2 3 3 9
..................................11分
由于事件A A ,B B ,C C 彼此相互独立
1 2 1 2 1 2
“恰有两人获得计算机三级证书”即为事件:..................13分
2 1 4 2 1 4 2 1 4 1
概率为P= × ×(1− )+ ×(1− )× +(1− )× × = .....................................15
5 2 9 5 2 9 5 2 9 3
分
18.解:(1)设 ,则 ,...........................................................................1分
即 ...............................................................................................................3分
化简得 ;
所以曲线 的方程为: ...............................................................................5分
(2)由(1)知曲线 的轨迹为圆,其圆心坐标为 ,半径
当直线 斜率不存在时, 的方程为 ,圆心到直线 的距离为1,所以
,故 满足题
意.......................................................................................................................7分
当直线 斜率存在时,设 的方程为 ,即 ,........................8分
圆心 到直线的距离为
所以 ....................................................................10分
解得
所以 的方程为 ,
即 的方程为 ......................................................................................................11分
综上所述,直线 的方程为 和 ...................................................................12分
1 1
(3)S = ×|BQ|×|TQ|= ×2×|TQ|=|TQ|=√|TB| 2 −4,..............................14分
∆TBQ 2 2
|4−0|
故|TB|最短时,S 有最小值,此时|TB|为圆心B到直线y=x的距离d= =2√2,
∆TBQ
√2
S 最 小 值 为
∆TBQ
2.................................................................................................................................17分
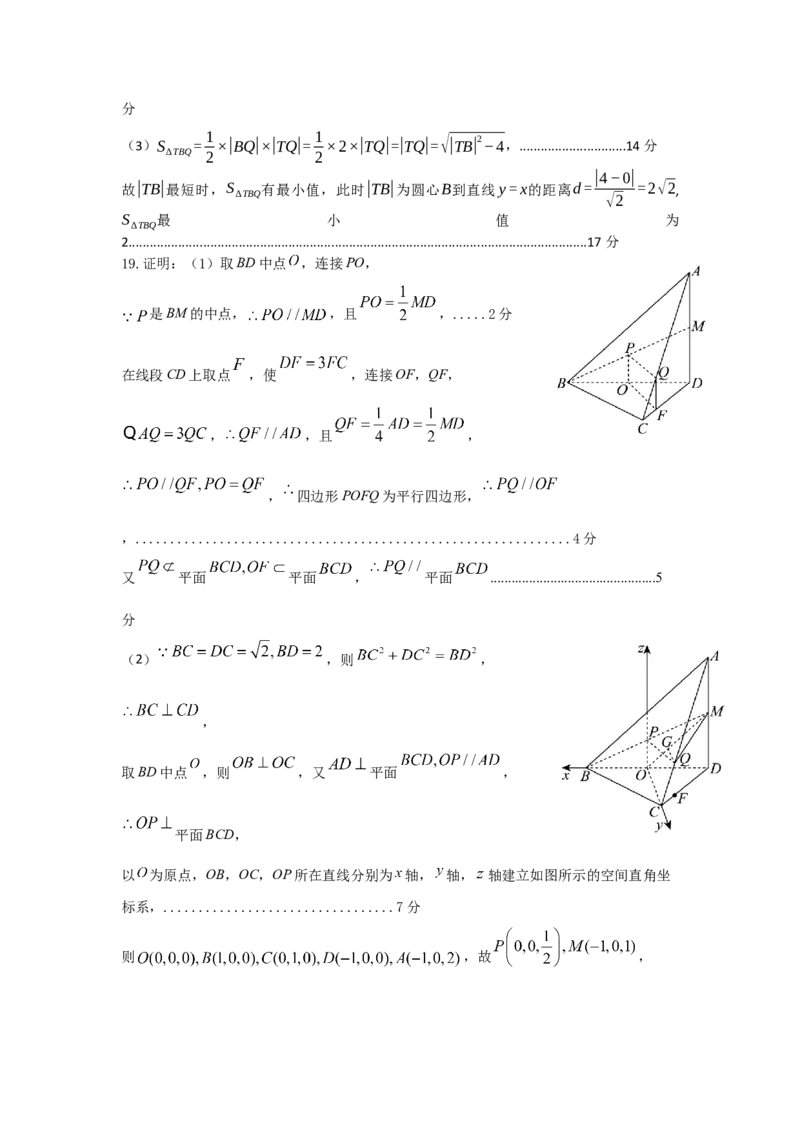
19.证明:(1)取BD中点 ,连接PO,
是BM的中点, ,且 ,.....2分
在线段CD上取点 ,使 ,连接OF,QF,
, ,且 ,
, 四边形POFQ为平行四边形,
,..............................................................4分
又 平面 平面 , 平面 ...............................................5
分
(2) ,则 ,
,
取BD中点 ,则 ,又 平面 ,
平面BCD,
以 为原点,OB,OC,OP所在直线分别为 轴, 轴, 轴建立如图所示的空间直角坐
标系,.................................7分
则 ,故 ,则 , , ,
,所以 ,
故 ,
易知平面 的一个法向量为 ,...................................9分
设平面 的一个法向量为⃗n=(x,y,z),
则 ,即 ,
取 ,则 , ,.....................................10分
设平面 与平面 的夹角为 ,
则 ,
所以平面 与平面 夹角的余弦值为 ..........................................................11分
(3)由(2)知 为BD中点, 为AD中点,连接OM,
,
点 为 内动点且 平面QGM,
又 平面ABD,平面 平面 ,
,故点 在OM上,..............................................12分
设 ,又 , , ,
则 ,
,...............................13分
易知平面 的一个法向量为 ,...................................14
分
设QG与平面 所成角为 ,则tanφ最大时, 最大,
,.............................16
分
所以当 时, 最大,此时 最大,
即当点 位于 中位线 靠近 的八等分点的第3个点处时,QG与平面 所
成角最大....................................................................................................................................17分