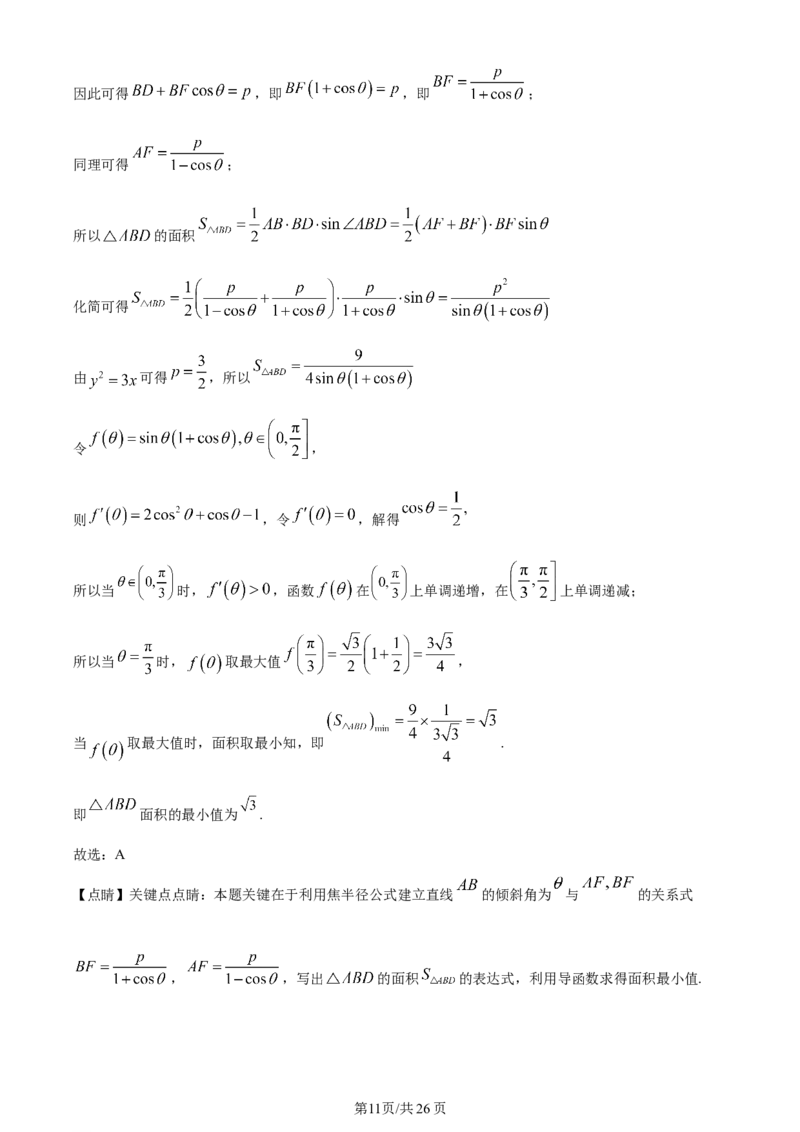文档内容
长安一中 2021 级高三第三次教学质量检测
数学(文科)试题
时间:120分钟 总分:150分
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. 设全集 ,集合 , ,则 等于( )
A. B. C. D.
【答案】B
【解析】
【分析】化简集合A,B,根据集合的交集、补集运算.
【详解】全集 ,集合 ,
或 ,
所以 ,
则 .
故选:B.
2. 已知复数 满足 ,则复数 的虚部为( )
A. B. C. D.
【答案】A
【解析】
【分析】利用复数除法运算和共轭复数定义可求得 ,由虚部定义可得结果.
【详解】 , ,
第1页/共26页
学科网(北京)股份有限公司则 的虚部为 .
故选:A.
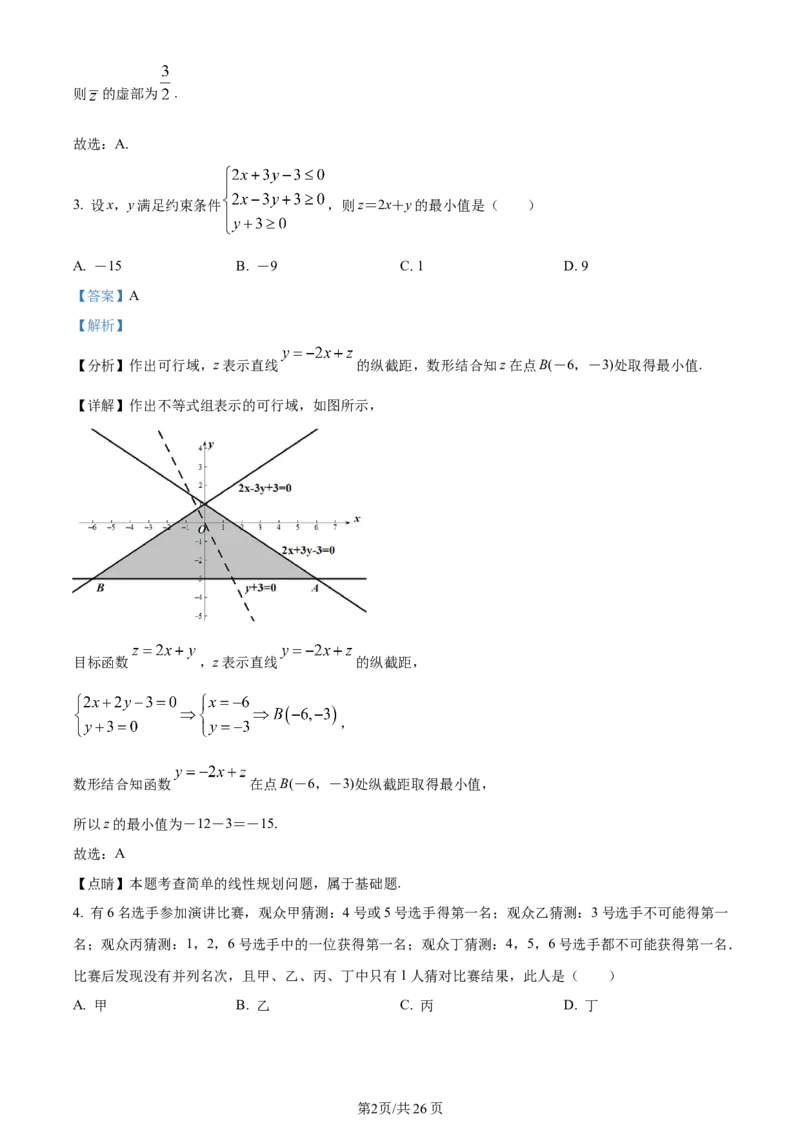
3. 设x,y满足约束条件 ,则z=2x+y的最小值是( )
A. -15 B. -9 C. 1 D. 9
【答案】A
【解析】
【分析】作出可行域,z表示直线 的纵截距,数形结合知z在点B(-6,-3)处取得最小值.
【详解】作出不等式组表示的可行域,如图所示,
目标函数 ,z表示直线 的纵截距,
,
数形结合知函数 在点B(-6,-3)处纵截距取得最小值,
所以z的最小值为-12-3=-15.
故选:A
【点睛】本题考查简单的线性规划问题,属于基础题.
4. 有6名选手参加演讲比赛,观众甲猜测:4号或5号选手得第一名;观众乙猜测:3号选手不可能得第一
名;观众丙猜测:1,2,6号选手中的一位获得第一名;观众丁猜测:4,5,6号选手都不可能获得第一名.
比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是( )
A. 甲 B. 乙 C. 丙 D. 丁
第2页/共26页
学科网(北京)股份有限公司【答案】D
【解析】
【分析】假设四人中任意一人猜对,根据合情推理即可求解.
【详解】假设甲猜对比赛结果,则乙也猜对比赛结果,所以假设不成立,所以甲没猜对比赛结果,即得第
一名的是1,2,3或6;若乙猜对比赛结果,则1,2或6号选手中的其中一名获得第一名,此时丙也猜对比赛
结果,所以乙也没有猜对比赛结果,所以3号选手获得第一名,则只有丁猜对了比赛结果.
故选: .
5. 若 为奇函数,则 的单调递增区间是( )
A. B.
C. D.
【答案】D
【解析】
【分析】由 为奇函数,求出 的值,利用复合函数的单调性特征求 的单调递增区间.
【详解】函数 为奇函数, 的定义域为 ,
由 ,∴ ,
函数 的定义域为 ,
函数 在定义域内单调递增,
当 时, 的单调递增区间为 ,
所以 的单调递增区间为 .
故选:D.
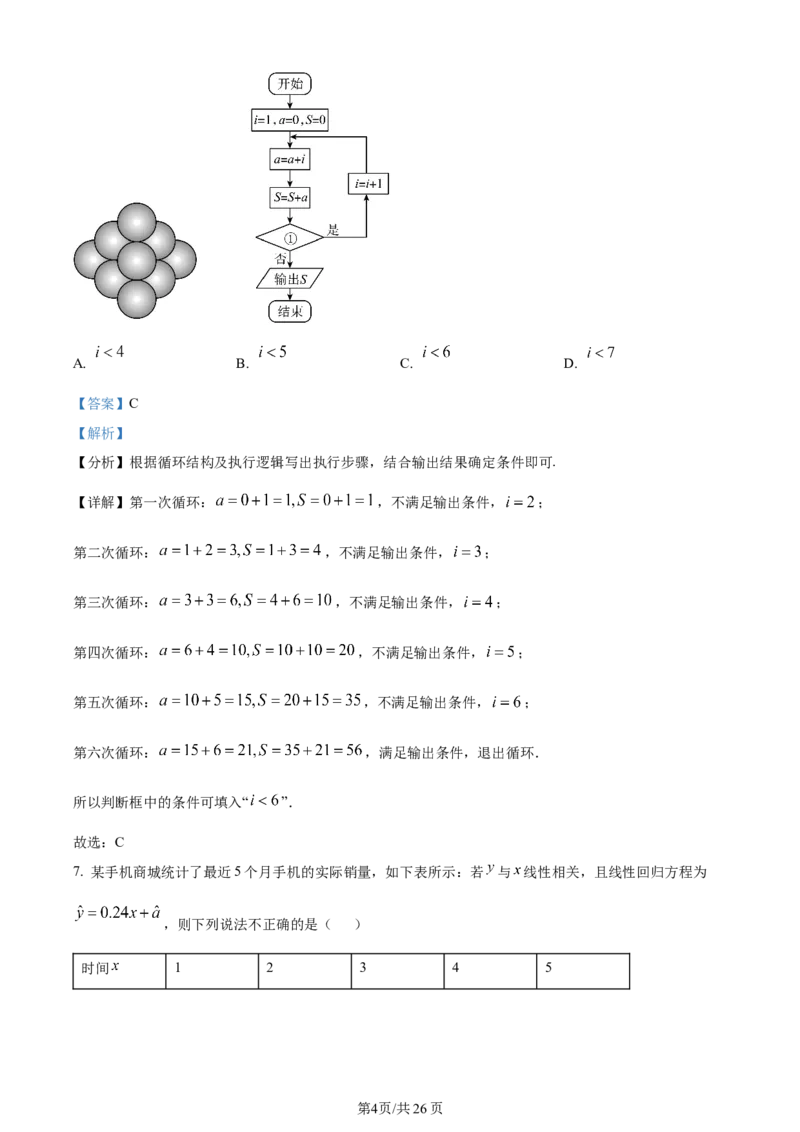
6. 南宋时期的数学家杨辉所著的《详解九章算法》中有一个如图所示的“三角垛”问题,在“三角垛”的最上
层放有一个球,第二层放有3个球,第三层放有6个球,……依此规律,其相应的程序框图如图所示.若
输出的 的值为56,则程序框图中 处可以填入( )
①
第3页/共26页
学科网(北京)股份有限公司A. B. C. D.
【答案】C
【解析】
【分析】根据循环结构及执行逻辑写出执行步骤,结合输出结果确定条件即可.
【详解】第一次循环: ,不满足输出条件, ;
第二次循环: ,不满足输出条件, ;
第三次循环: ,不满足输出条件, ;
第四次循环: ,不满足输出条件, ;
第五次循环: ,不满足输出条件, ;
第六次循环: ,满足输出条件,退出循环.
所以判断框中的条件可填入“ ”.
故选:C
7. 某手机商城统计了最近5个月手机的实际销量,如下表所示:若 与 线性相关,且线性回归方程为
,则下列说法不正确的是( )
时间 1 2 3 4 5
第4页/共26页
学科网(北京)股份有限公司销 售 量
0.5 0.8 1.0 1.2 1.5
(千只)
A. 由题中数据可知,变量 与 正相关
B. 线性回归方程 中
C. 可以预测 时该商场手机销量约为1.72(千只)
D. 当 时,残差为
【答案】ABC
【解析】
【分析】根据表格中的数据的变换趋势,平均数的计算公式,以及回归直线方程,逐项判定,即可求解.
【详解】对于A中,从数据可得 随着 的增加而增加,所以变量 与 正相关,所以A正确;
对于B中,由表中数据知 ,
则样本中心点为 ,将样本中心点 ,代入 中,
可得 ,所以B正确;
对于C中,当 时,该商场 手机销售量约为 (千只),
所以C正确;
对于D中,线性回归方程为 ,
当 时,可得 ,残差为 ,所以D错误.
故选:ABC.
8. 折扇(图1)是具有独特风格的中国传统工艺品,炎炎夏季,手拿一把折扇,既可解暑,又有雅趣.图
2中的扇形 为一把折扇展开后的平面图,其中 , ,设向量
, ,若 ,则实数 的值为( )
第5页/共26页
学科网(北京)股份有限公司A. 1 B. 3 C. 7 D. 14
【答案】D
【解析】
【 分 析 】 先 利 用 题 意 算 出 , 然 后 利 用 数 量 积 的 运 算 律 对
进行化简,即可求解
【详解】因为 , ,
所以 ,
因为向量 , , ,
所以 ,
即 ,解得
故选:D
9. 已知双曲线 的离心率大于 ,则实数 的取值范围是( )
A. B. C. D.
【答案】A
【解析】
【分析】根据双曲线方程,讨论实轴位置,求出离心率,由已知离心率范围列出不等式可解得 的范围.
【详解】当双曲线实轴在 轴上时, ,解得 ,
第6页/共26页
学科网(北京)股份有限公司此时 ,所以 ,
解得 ,所以 ,
当双曲线实轴在 轴上时, ,解得 ,不符合题意.
综上,解得 .
故选:A.
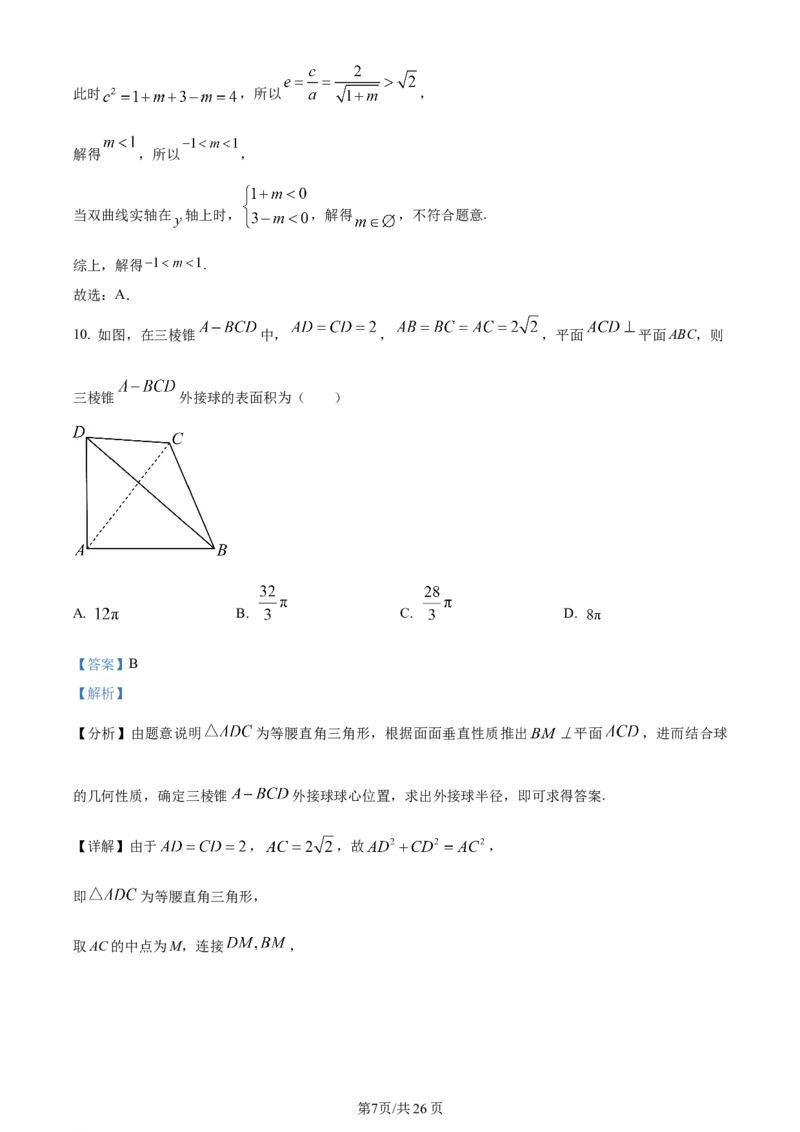
10. 如图,在三棱锥 中, , ,平面 平面ABC,则
三棱锥 外接球的表面积为( )
A. B. C. D.
【答案】B
【解析】
【分析】由题意说明 为等腰直角三角形,根据面面垂直性质推出 平面 ,进而结合球
的几何性质,确定三棱锥 外接球球心位置,求出外接球半径,即可求得答案.
【详解】由于 , ,故 ,
即 为等腰直角三角形,
取AC的中点为M,连接 ,
第7页/共26页
学科网(北京)股份有限公司因为 ,即 为正三角形,故 ,
由于平面 平面 ,平面 平面 , 平面 ,
故 平面 , 平面 ,故 ;
又M为 的外心,
则三棱锥 外接球的球心必在BM上,
设 的中心为O,则O在BM上且 ,
而 ,
则 ,
即 ,
即O点即为三棱锥 外接球的球心,
故外接球半径为 ,所以外接球表面积为 ,
故选:B
【点睛】关键点睛:解答本题的关键在于要能根据条件,结合球的几何性质,确定出三棱锥外接球球心的
位置,进而求得半径.
11. 已知角 , 终边上有一点 ,则 ( )
第8页/共26页
学科网(北京)股份有限公司A. 2 B. C. D.
【答案】C
【解析】
【分析】根据弦切互化,结合正切和差角公式,即可得 ,结合角的范围即可求解.
【详解】
,故 , .
又 , ,
故 在第三象限,故 , .
故选:C.
12. 过抛物线 的焦点F作直线交C于A,B,过A和原点的直线交 于D,则 面
积的最小值为( )
A. B. 2 C. D.
【答案】A
【解析】
【分析】根据题意可得焦点 ,准线 ,设直线 的倾斜角为 ,则直线 的方程为
;联立抛物线方程可得 ,联立直线 和准线方程 可得
第9页/共26页
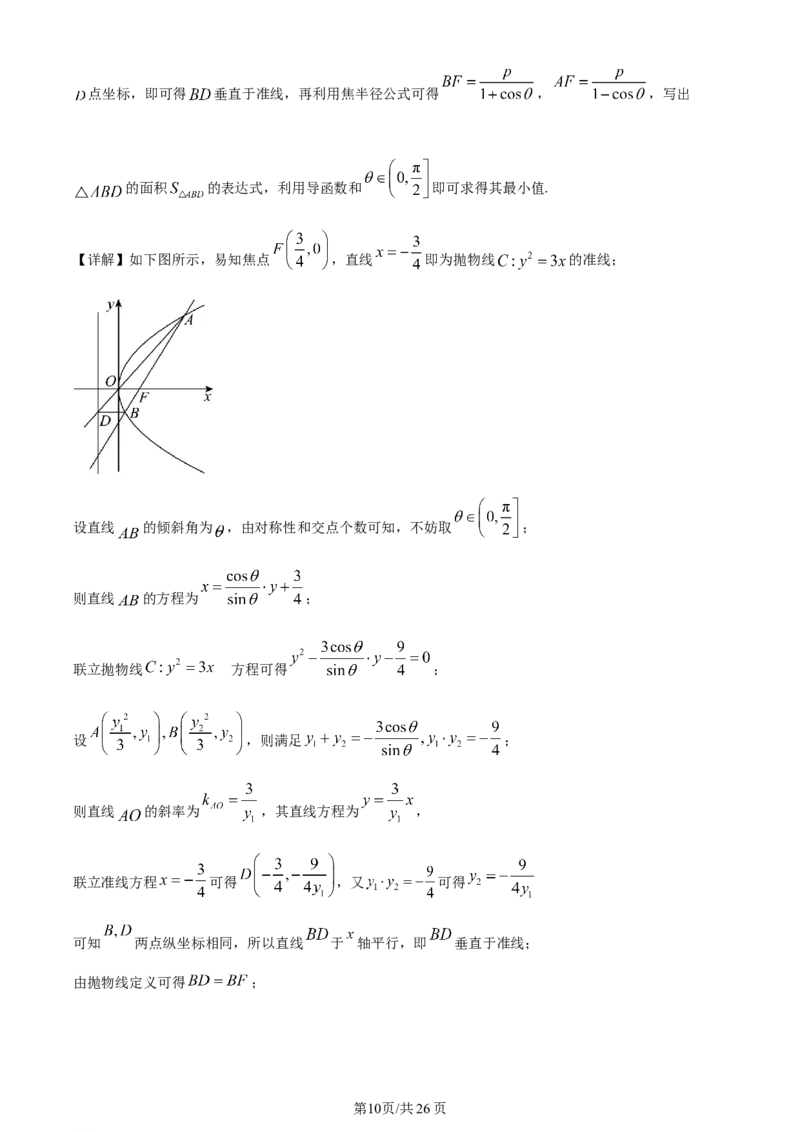
学科网(北京)股份有限公司点坐标,即可得 垂直于准线,再利用焦半径公式可得 , ,写出
的面积 的表达式,利用导函数和 即可求得其最小值.
【详解】如下图所示,易知焦点 ,直线 即为抛物线 的准线;
设直线 的倾斜角为 ,由对称性和交点个数可知,不妨取 ;
则直线 的方程为 ;
联立抛物线 的方程可得 ;
设 ,则满足 ;
则直线 的斜率为 ,其直线方程为 ,
联立准线方程 可得 ,又 可得
可知 两点纵坐标相同,所以直线 于 轴平行,即 垂直于准线;
由抛物线定义可得 ;
第10页/共26页
学科网(北京)股份有限公司因此可得 ,即 ,即 ;
同理可得 ;
所以 的面积
化简可得
由 可得 ,所以
令 ,
则 ,令 ,解得
所以当 时, ,函数 在 上单调递增,在 上单调递减;
所以当 时, 取最大值 ,
当 取最大值时,面积取最小知,即 .
即 面积的最小值为 .
故选:A
【点睛】关键点点睛:本题关键在于利用焦半径公式建立直线 的倾斜角为 与 的关系式
, ,写出 的面积 的表达式,利用导函数求得面积最小值.
第11页/共26页
学科网(北京)股份有限公司二、填空题:本题共4小题,每小题5分,共20分.
13. 已知函数 (其中 )在 处的切线为 ,则直线 过定点的坐标为__________.
【答案】
【解析】
【分析】利用导数的几何意义求出切线方程,从而可求出其过的定点
【详解】根据题意:函数 在 处有切线, 切点为 ,
又 ,故切线斜率为 ,
直线 的方程为 ,
该直线过定点的坐标为 .
故答案为:
14. 等差数列 中的 是函数 的极值点,则 __.
【答案】
【解析】
【分析】求得 ,结合题意,得到 是方程 的两个根,再由等
差数列的性质和对数的运算性质,即可求解.
【详解】由函数 ,可得 ,
因为 是函数 的极值点,即 是方程 的两个根,
可得 ,又由 ,所以 .
故答案为: .
第12页/共26页
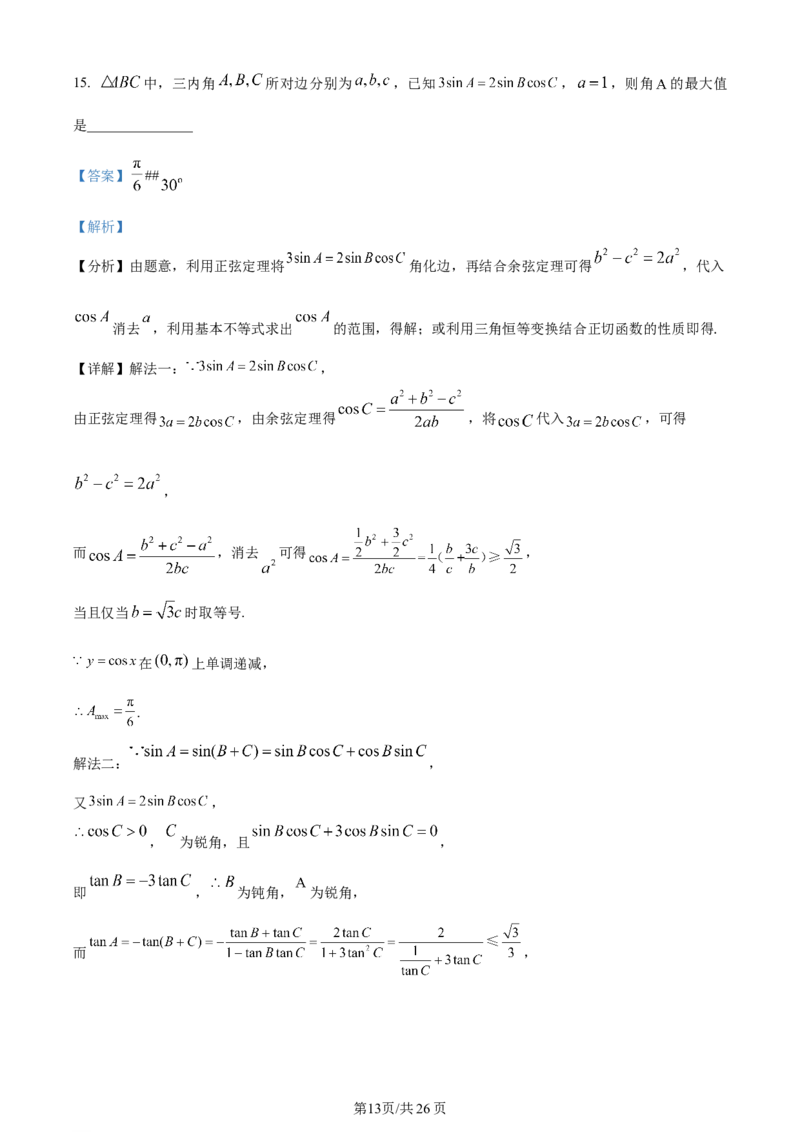
学科网(北京)股份有限公司15. 中,三内角 所对边分别为 ,已知 , ,则角 的最大值
是_______________
【答案】 ##
【解析】
【分析】由题意,利用正弦定理将 角化边,再结合余弦定理可得 ,代入
消去 ,利用基本不等式求出 的范围,得解;或利用三角恒等变换结合正切函数的性质即得.
【详解】解法一: ,
由正弦定理得 ,由余弦定理得 ,将 代入 ,可得
,
而 ,消去 可得 ,
当且仅当 时取等号.
在 上单调递减,
.
解法二: ,
又 ,
, 为锐角,且 ,
即 , 为钝角, 为锐角,
而 ,
第13页/共26页
学科网(北京)股份有限公司在 上单调递增,
.
故答案为:
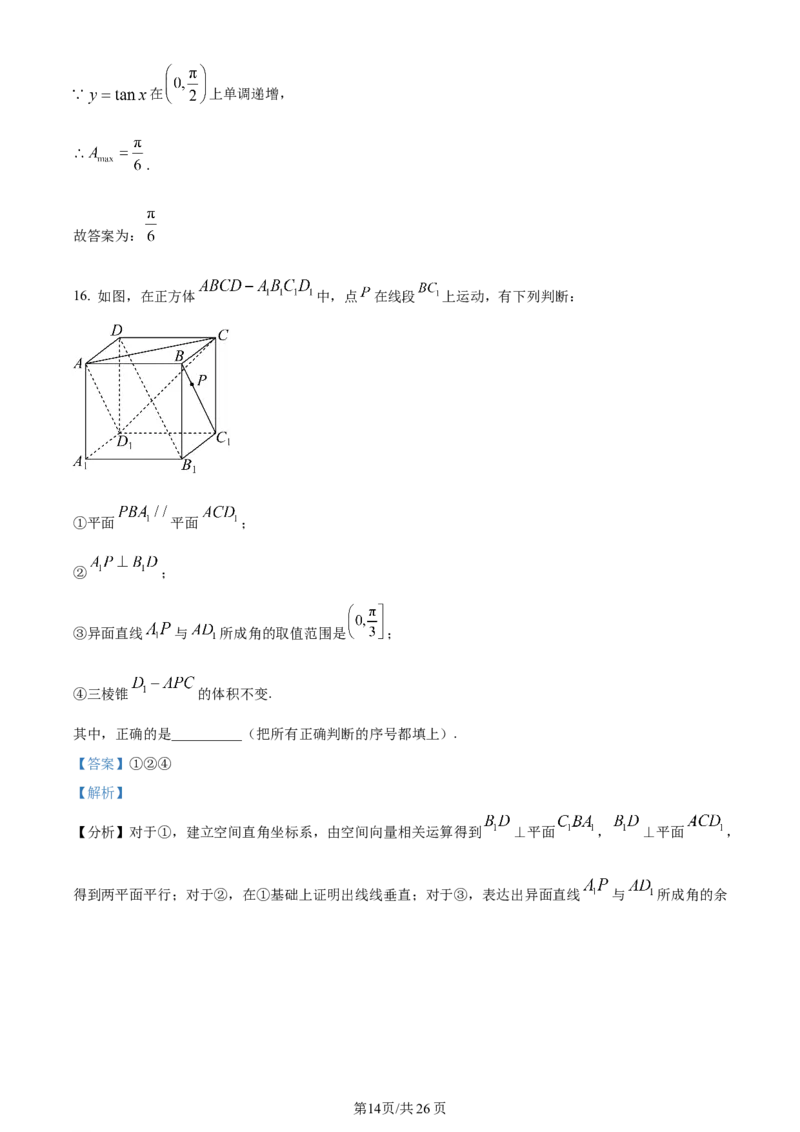
16. 如图,在正方体 中,点 在线段 上运动,有下列判断:
①平面 平面 ;
② ;
③异面直线 与 所成角的取值范围是 ;
④三棱锥 的体积不变.
其中,正确的是__________(把所有正确判断的序号都填上).
【答案】①②④
【解析】
【分析】对于①,建立空间直角坐标系,由空间向量相关运算得到 ⊥平面 , ⊥平面 ,
得到两平面平行;对于②,在①基础上证明出线线垂直;对于③,表达出异面直线 与 所成角的余
第14页/共26页
学科网(北京)股份有限公司弦值为 ,当 和 两种情况,求出异面直线 与
所成角范围;D选项,由线面平行结合等体积法得到三棱锥体积为定值.
【详解】对于①,设正方体 的棱长为1,
则 ,
故 , ,
,
故 ⊥ , ⊥ ,
又 , 平面 ,
故 ⊥平面 ,
又 在线段 上运动,故 ⊥平面 ,
又 ,
,
故 ⊥ , ⊥ ,
又 , 平面 ,
故 ⊥平面 ,
所以平面 平面 ,①正确;
第15页/共26页
学科网(北京)股份有限公司对于②,由①可得 ⊥平面 ,又 平面 ,
所以 ,②正确;
对于③,设 ,
则 ,
设异面直线 与 所成角大小为 ,
则
,
当 时, ,故 ,
当 时, ,
又 在 上单调递减,故 ,
综上,异面直线 与 所成角的取值范围是 ,③错误;
第16页/共26页
学科网(北京)股份有限公司对于④,因为 ,所以 ,
因为 平面 , 平面 ,所以 平面 ,
故又 在线段 上运动,故 为定值,
故 ,体积不变.,④正确.
故答案为:①②④
三、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 设数列 的前n项和为 , .
(1)求证数列 为等比数列,并求数列 的通项公式 .
(2)若数列 的前m项和 ,求m的值,
【答案】(1)证明见解析,
(2)7
【解析】
【分析】(1)利用数列中 与 的关系,得 ,可证明数列 为等比数列,可求数列
的通项公式 .
(2)利用裂项相消求数列 的前m项和 ,由 求m的值.
【小问1详解】
因为 ,所以当 时, ,解得 .
当 时, ,则 ,
整理得 ,故 , ,
第17页/共26页
学科网(北京)股份有限公司所以数列 是首项为2,公比为2的等比数列,所以 .所以
【小问2详解】
,
数列 的前m项和
,
则 ,则 ,则 ,解得 ,故m的值为7.
18. 某重点大学为了解准备保研或者考研的本科生每天课余学习时间,随机抽取了 名这类大学生进行
调查,将收集到的课余学习时间(单位: )整理后得到如下表格:
课余学习时间
人数
(1)估计这 名大学生每天课余学习时间的中位数;
(2)根据分层抽样的方法从课余学习时间在 和 ,这两组中抽取 人,再从这 人中随机抽取
人,求抽到的 人的课余学习时间都在 的概率.
【答案】(1)
(2)
【解析】
【分析】(1)根据频数分布表估计中位数的方法直接求解即可;
(2)根据分层抽样原则可确定从 和 两组中抽取的人数,采用列举法可得所有基本事件和满足
题意的基本事件个数,根据古典概型概率公式可求得结果.
【小问1详解】
第18页/共26页
学科网(北京)股份有限公司, ,
这 名大学生每天课余学习时间的中位数位于 之间,
则中位数为 .
【小问2详解】
由题意知:从课余学习时间在 这一组抽取 人,分别记为 ,从课余学习时间在
这一组抽取 人,分别记为 ;
从这 人中随机抽取 人,所有的基本事件为:
,共 个基本事件;
其 中 “ 抽 到 的 人 的 课 余 学 习 时 间 都 在 ” 包 含 的 基 本 事 件 为 :
,共 个基本事件;
抽到的 人的课余学习时间都在 的概率 .
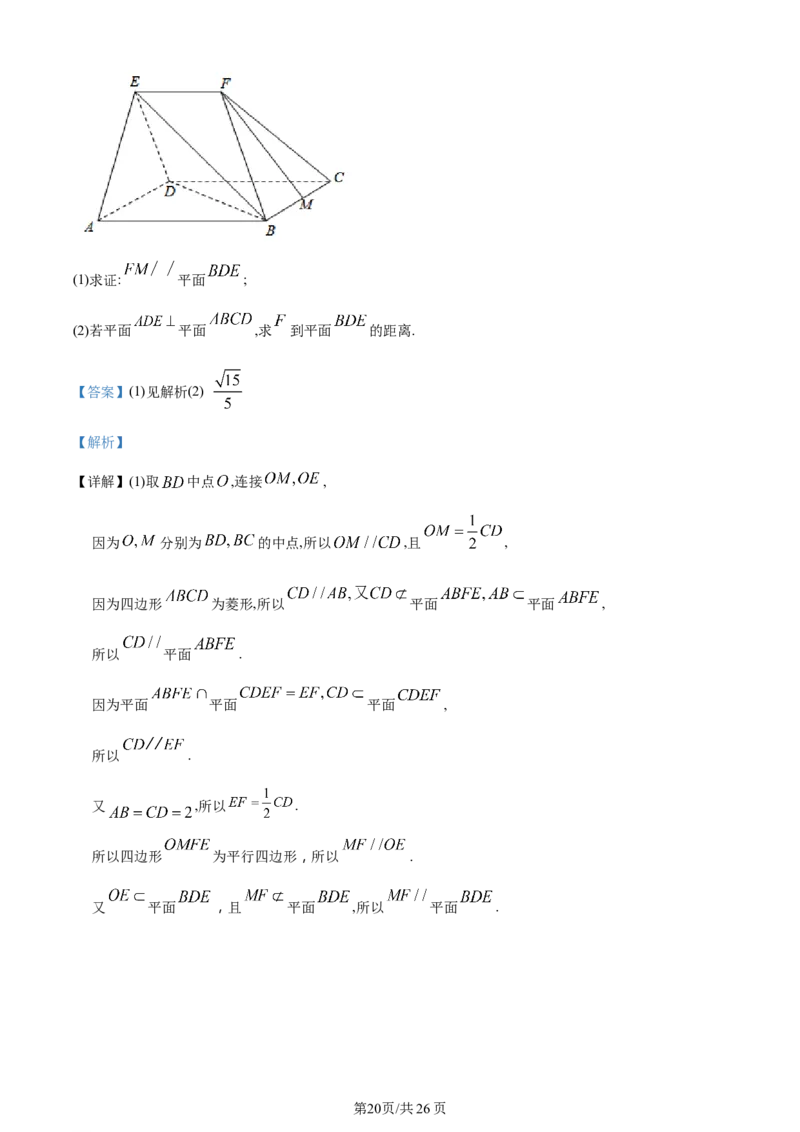
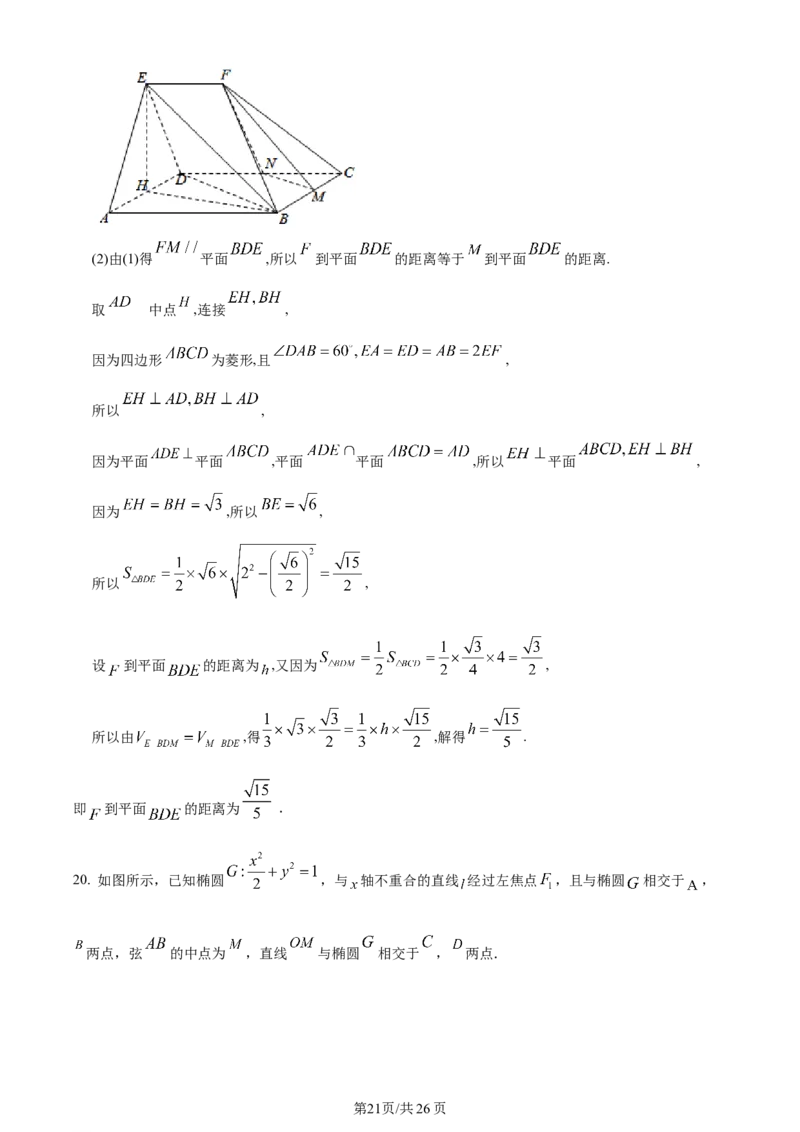
19. 在如图所示的五面体 中,四边形 为菱形,且
为 中点.
第19页/共26页
学科网(北京)股份有限公司(1)求证: 平面 ;
(2)若平面 平面 ,求 到平面 的距离.
【答案】(1)见解析(2)
【解析】
【详解】(1)取 中点 ,连接 ,
因为 分别为 的中点,所以 ,且 ,
因为四边形 为菱形,所以 平面 平面 ,
所以 平面 .
因为平面 平面 平面 ,
所以 .
又 ,所以 .
所以四边形 为平行四边形,所以 .
又 平面 ,且 平面 ,所以 平面 .
第20页/共26页
学科网(北京)股份有限公司(2)由(1)得 平面 ,所以 到平面 的距离等于 到平面 的距离.
的
取 中点 ,连接 ,
因为四边形 为菱形,且 ,
所以 ,
因为平面 平面 ,平面 平面 ,所以 平面 ,
因为 ,所以 ,
所以 ,
设 到平面 的距离为 ,又因为 ,
所以由 ,得 ,解得 .
即 到平面 的距离为 .
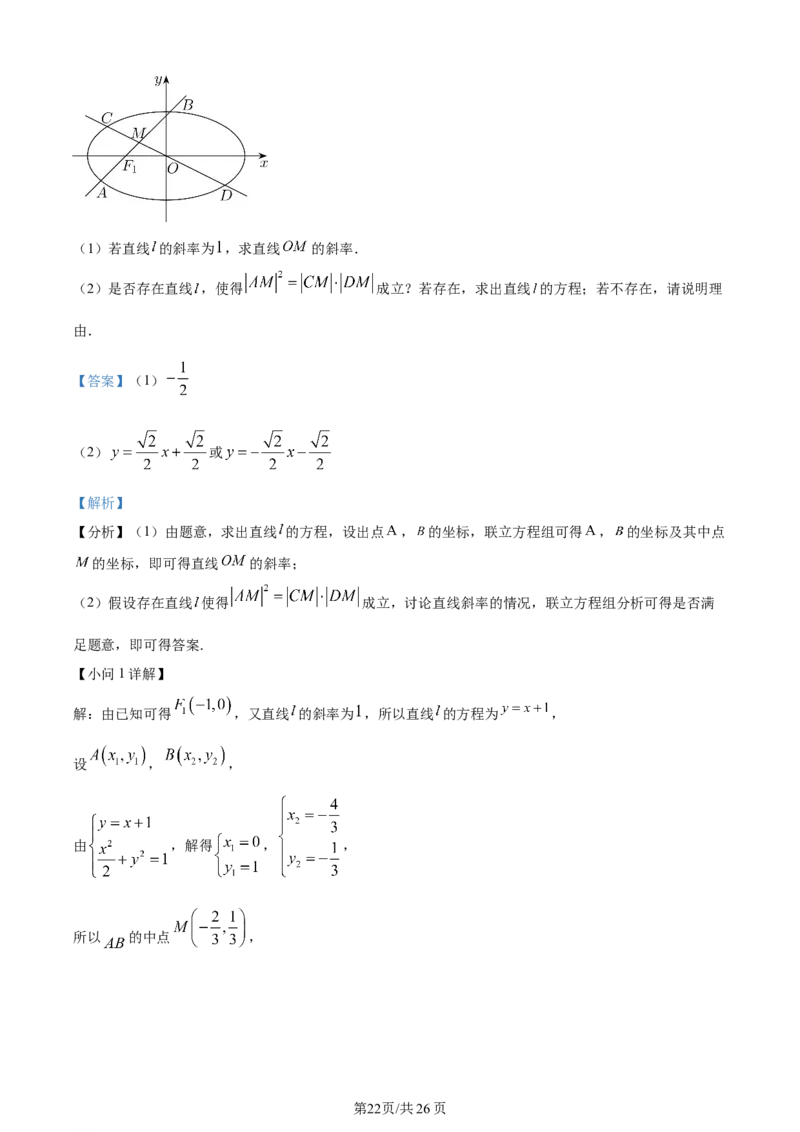
20. 如图所示,已知椭圆 ,与 轴不重合的直线 经过左焦点 ,且与椭圆 相交于 ,
两点,弦 的中点为 ,直线 与椭圆 相交于 , 两点.
第21页/共26页
学科网(北京)股份有限公司(1)若直线 的斜率为 ,求直线 的斜率.
(2)是否存在直线 ,使得 成立?若存在,求出直线 的方程;若不存在,请说明理
由.
【答案】(1)
(2) 或
【解析】
【分析】(1)由题意,求出直线 的方程,设出点 , 的坐标,联立方程组可得 , 的坐标及其中点
的坐标,即可得直线 的斜率;
(2)假设存在直线 使得 成立,讨论直线斜率的情况,联立方程组分析可得是否满
足题意,即可得答案.
【小问1详解】
解:由已知可得 ,又直线 的斜率为 ,所以直线 的方程为 ,
设 , ,
由 ,解得 , ,
所以 的中点 ,
第22页/共26页
学科网(北京)股份有限公司于是直线 的斜率为 ;
【小问2详解】
解:假设存在直线 ,使得 成立,
当直线 的斜率不存在时, 的中点 ,
所以 , ,矛盾;
故直线斜率存在,可设直线 的方程为 ( ),
联立直线与椭圆方程得 ,
则 , ,
于是 ,
点 的坐标为 ,
,
直线 的方程为 ,
联立椭圆于直线 ,得 ,
设 ,则 ,
由题意 ,
第23页/共26页
学科网(北京)股份有限公司即 ,
化简得 ,故 ,
所以直线 的方程为 或 .
【点睛】(1)解答直线与椭圆的题目时,时常把两个曲线的方程联立,消去x(或y)建立一元二次方程,然后
借助根与系数的关系,并结合题设条件建立有关参变量的等量关系.
(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形.
21. 已知 且 ,函数 .
(1)当 时,求 的单调区间;
(2)若曲线 与直线 有且仅有两个交点,求a的取值范围.
【答案】(1) 上单调递增; 上单调递减;(2) .
【解析】
【分析】(1)求得函数的导函数,利用导函数的正负与函数的单调性的关系即可得到函数的单调性;
(2)方法一:利用指数对数的运算法则,可以将曲线 与直线 有且仅有两个交点等价转化
为方程 有两个不同的实数根,即曲线 与直线 有两个交点,利用导函数研究
的单调性,并结合 的正负,零点和极限值分析 的图象,进而得到 ,发现这
正好是 ,然后根据 的图象和单调性得到 的取值范围.
第24页/共26页
学科网(北京)股份有限公司【详解】(1)当 时, ,
令 得 ,当 时, ,当 时, ,
∴函数 在 上单调递增; 上单调递减;
(2)[方法一]【最优解】:分离参数
,
设函数 ,
则 ,令 ,得 ,
在 内 , 单调递增;
在 上 , 单调递减;
,
又 ,当 趋近于 时, 趋近于0,
所以曲线 与直线 有且仅有两个交点,即曲线 与直线 有两个交点的充分
必要条件是 ,这即是 ,
所以 的取值范围是 .
[方法二]:构造差函数
由 与直线 有且仅有两个交点知 ,即 在区间 内有两个解,取对数得
方程 在区间 内有两个解.
第25页/共26页
学科网(北京)股份有限公司构造函数 ,求导数得 .
当 时, 在区间 内单调递增,所以,
在 内最多只有一个零点,不符合题意;
当 时, ,令 得 ,当 时, ;当 时,
;所以,函数 的递增区间为 ,递减区间为 .
由于 ,
当 时,有 ,即 ,由函数 在 内有两个零点知
,所以 ,即 .
构造函数 ,则 ,所以 的递减区间为 ,递增区间为 ,
所以 ,当且仅当 时取等号,故 的解为 且 .
的
所以,实数a 取值范围为 .
[方法三]分离法:一曲一直
曲线 与 有且仅有两个交点等价为 在区间 内有两个不相同的解.
因为 ,所以两边取对数得 ,即 ,问题等价为 与
有且仅有两个交点.
①当 时, 与 只有一个交点,不符合题意.
第26页/共26页
学科网(北京)股份有限公司②当 时,取 上一点 在点 的切线方程
为 ,即 .
当 与 为同一直线时有 得
直线 的斜率满足: 时, 与 有且仅有两个交点.
记 ,令 ,有 . 在区间 内单调递增;
在区间 内单调递减; 时, 最大值为 ,所当 且
时有 .
综上所述,实数a的取值范围为 .
[方法四]:直接法
.
因为 ,由 得 .
当 时, 在区间 内单调递减,不满足题意;
当 时, ,由 得 在区间 内单调递增,由 得
第27页/共26页
学科网(北京)股份有限公司在区间 内单调递减.
因为 ,且 ,所以 ,即 ,即
,两边取对数,得 ,即 .
令 ,则 ,令 ,则 ,所以 在区间 内单调递增,
在区间 内单调递减,所以 ,所以 ,则 的解为 ,所以
,即 .
的
故实数a 范围为 .]
【整体点评】本题考查利用导数研究函数的单调性,根据曲线和直线的交点个数求参数的取值范围问题,
属较难试题,
方法一:将问题进行等价转化,分离参数,构造函数,利用导数研究函数的单调性和最值,图象,利用数
形结合思想求解.
方法二:将问题取对,构造差函数,利用导数研究函数的单调性和最值.
方法三:将问题取对,分成 与 两个函数,研究对数函数过原点的切线问题,将切
线斜率与一次函数的斜率比较得到结论.
方法四:直接求导研究极值,单调性,最值,得到结论.
请考生在第22,23题中任选一题作答,每题10分,如果多做,则按所做的第一题计分.
【选修4-4:坐标系与参数方程】
22. 在直角坐标系 中,曲线 的参数方程为 ( 为参数),以坐标原点 为极点, 轴的
第28页/共26页
学科网(北京)股份有限公司正半轴为极轴建立极坐标系,直线 的极坐标方程为 .
(1)求 的普通方程和 的直角坐标方程;
(2)若 与 有两个不同的交点,求实数 的取值范围.
【答案】(1) ,其中 ;
(2)
【解析】
【分析】(1)根据题意,消去参数 ,得到曲线 的普通方程,结合极坐标与直角的互化公式,即可求得
直线 的直角坐标方程;
(2)根据题意,联立方程组,方程有两个非负实根,列出不等式组,即可求解.
【小问1详解】
解:由曲线 的参数方程为 ( 为参数),
消去参数 ,可得 ,其中 ,
又由直线 的极坐标方程为 ,即 ,
因为 ,可得 ,即 ,
所以曲线 的普通方程为 ,其中 ,
直线 的直角坐标方程为 .
【小问2详解】
解:若直线 与曲线 有两个不同的交点,则 有两组不同的解,
第29页/共26页
学科网(北京)股份有限公司整理得 ,
则方程有两个非负实根,即 ,解得 ,
所以实数 的取值范围是 .
【选修4-5:不等式选讲】
23. 已知函数 的图象关于直线 对称.
(1)求 的最小值;
(2)设 , 均为正数,且 ,求 的最小值.
【答案】(1)4; (2)
【解析】
【分析】(1)先整理 ,再利用题意中的对称求出 ,然后用三角不等式求出最小值即可;
(2)由(1)可得 ,然后利用“1”的妙用和基本不等式即可求解
【小问1详解】
,
令 ,解得 ;令 ,解得 ,
因为函数 的图象关于直线 对称,
所以 ,解得 ,
第30页/共26页
学科网(北京)股份有限公司所以 ,当且仅当 时,取等号,
故 的最小值为4;
【小问2详解】
由(1)可得 ,即 ,
所以 ,
当且仅当 即 时,取等号,
故 的最小值为
第31页/共26页
学科网(北京)股份有限公司