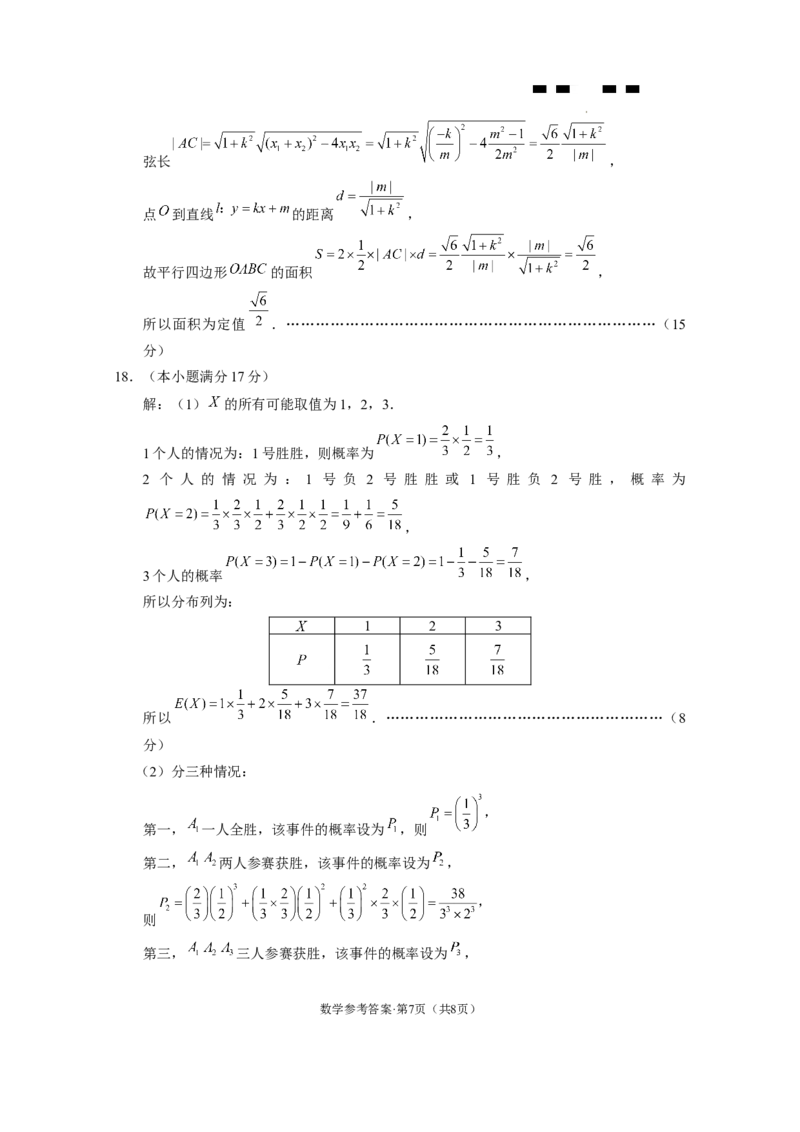文档内容
数学参考答案
一、单项选择题(本大题共8小题,每小题5分,共40分)
题号 1 2 3 4 5 6 7 8
答案 A C B D C A B C
【解析】
1.由 ,所以 ,故选A.
2.由 ,所以 ,对应的坐标为 ,故选C.
3.A. ,在 的切线斜率为 0,不符合;B. 在
的切线斜率为1,所以切线为 ,成立;C.D.两个函数均不经过
,不符合,故选B.
4.由定义, ,当 ,合题意;当 ,化简得 ,由
于横坐标 ,角在一、四象限,所以 ,故选D.
5.设出每一秒钟的路程为数列 ,由题意可知 为等差数列, 则数列首项 ,公
差 ,由求和公式有 ,解得 ,故选C.
6.令 ,则 ,
将假设代入,则 ,由基本不等式:
所以 ,可得 ,当且仅当 时取等号,面积最大,
故选A.
7.由题意可知: ,且
即 当 时, ,由于
,所以满足 的 的最小值为51,故选B.
数学参考答案·第1页(共8页)
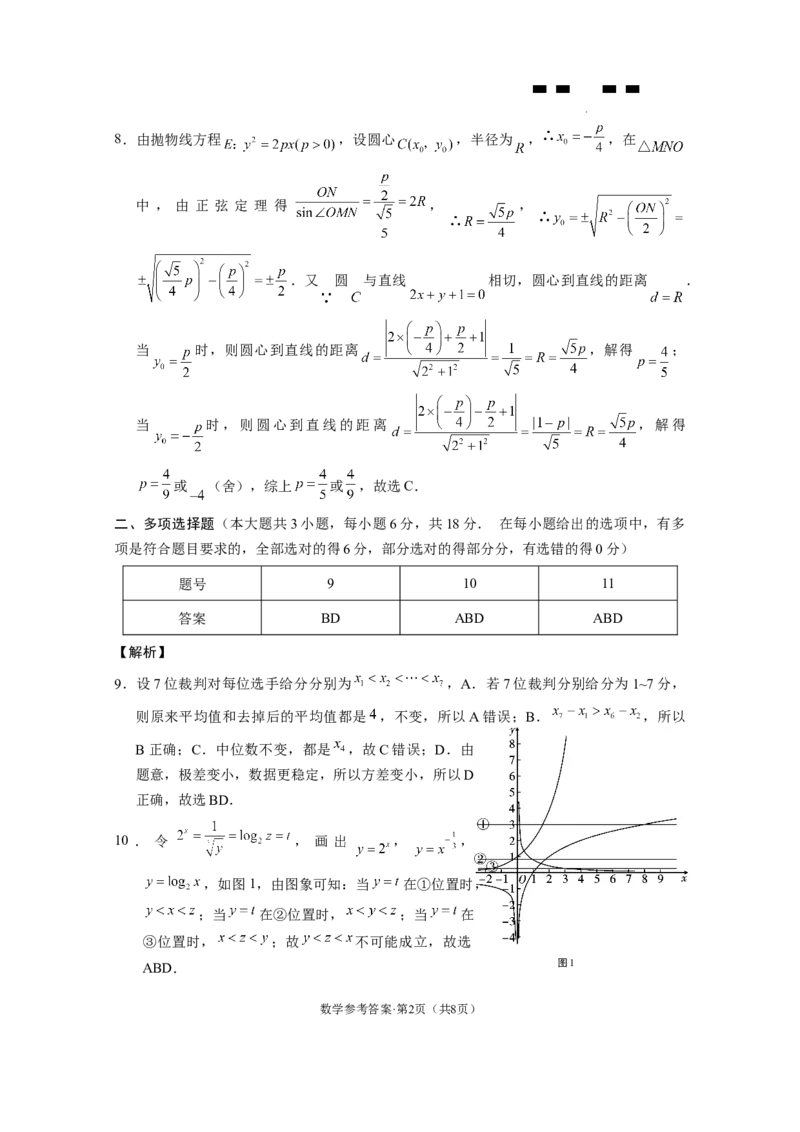
学科网(北京)股份有限公司8.由抛物线方程 ,设圆心 ,半径为 , ,在
中 , 由 正 弦 定 理 得 , ,
.又 圆 与直线 相切,圆心到直线的距离 .
当 时,则圆心到直线的距离 ,解得 ;
当 时,则圆心到直线的距离 ,解得
或 (舍),综上 或 ,故选C.
二、多项选择题(本大题共3小题,每小题6分,共18分. 在每小题给出的选项中,有多
项是符合题目要求的,全部选对的得6分,部分选对的得部分分,有选错的得0分)
题号 9 10 11
答案 BD ABD ABD
【解析】
9.设7位裁判对每位选手给分分别为 ,A.若7位裁判分别给分为1~7分,
则原来平均值和去掉后的平均值都是 ,不变,所以A错误;B. ,所以
B正确;C.中位数不变,都是 ,故C错误;D.由
题意,极差变小,数据更稳定,所以方差变小,所以D
正确,故选BD.
10 . 令 , 画 出 , ,
,如图1,由图象可知:当 在①位置时,
;当 在②位置时, ;当 在
③位置时, ;故 不可能成立,故选
ABD.
图1
数学参考答案·第2页(共8页)
学科网(北京)股份有限公司11.由棱长为2,可得正八面体上半部分的斜高为 ,高为 ,
则正八面体的体积为 .此正八面体的外接球
的球心为 ,半径为 ,所以外接球的体积为 ,A正确;由于 到平面
的距离等于 到平面 的距离,在 中,过 作 的垂线,垂足为 ,
则 平面 .由 ,得 ,平面 截正八面体的外接
球所得截面是圆,其半径 ,所以所得截面的面积为
,B正确;甲随机选择的情况有 种,乙随机选择的情况有 种,
甲选择的三个点构成正三角形,只有一种情况:甲从上下两个点中选一个,从中间四个
点中选相邻两个,共有 种,甲构成正三角形的概率为 ,故C错误;乙构
成正三角形,只有一种情况:上面四个面的中心中选一个点且从下面四个面的中心选相
对的两个点,或下面四个面的中心中选一个点且从上面四个面的中心选相对的两个点,
共有 种,概率为 ;甲能构成正三角形的概率为 ,所以甲与乙均能构成
正三角形的概率为 ,故D选项正确,故选ABD.
三、填空题(本大题共3小题,每小题5分,共15分)
题号 12 13 14
答案
【解析】
12 . 因 为 , 且 , 即 , 有
,所以 .
13.设 ,因为当 时, 单调递增;当 时,
单调递减,所以当 时, 有最大值.又因为 是减函数,所以只需考虑
时, 的大小情况即可.当 时,比较 与 的大小.因为
数学参考答案·第3页(共8页)
学科网(北京)股份有限公司, 所
以令 ,得 ,解得 .因此,当 时, 取最大值.
14.在 中,由正弦定理得: ,由
于 , 所 以 . 则 有 :
.
,由
,可得 .
四、解答题(共77分.解答应写出文字说明,证明过程或演算步骤)
15.(本小题满分13分)
(1)解:当
两式相减得: ,所以 .
当 且 ,可得 ,也满足,
由 ,则 为等比数列, ,
所以 .…………………………………………………………………………(7
分)
(2)证明: ,当 时, 成立;
当 时,
所以 成立.
………………………………………………………………………………………(13
分)
16.(本小题满分15分)
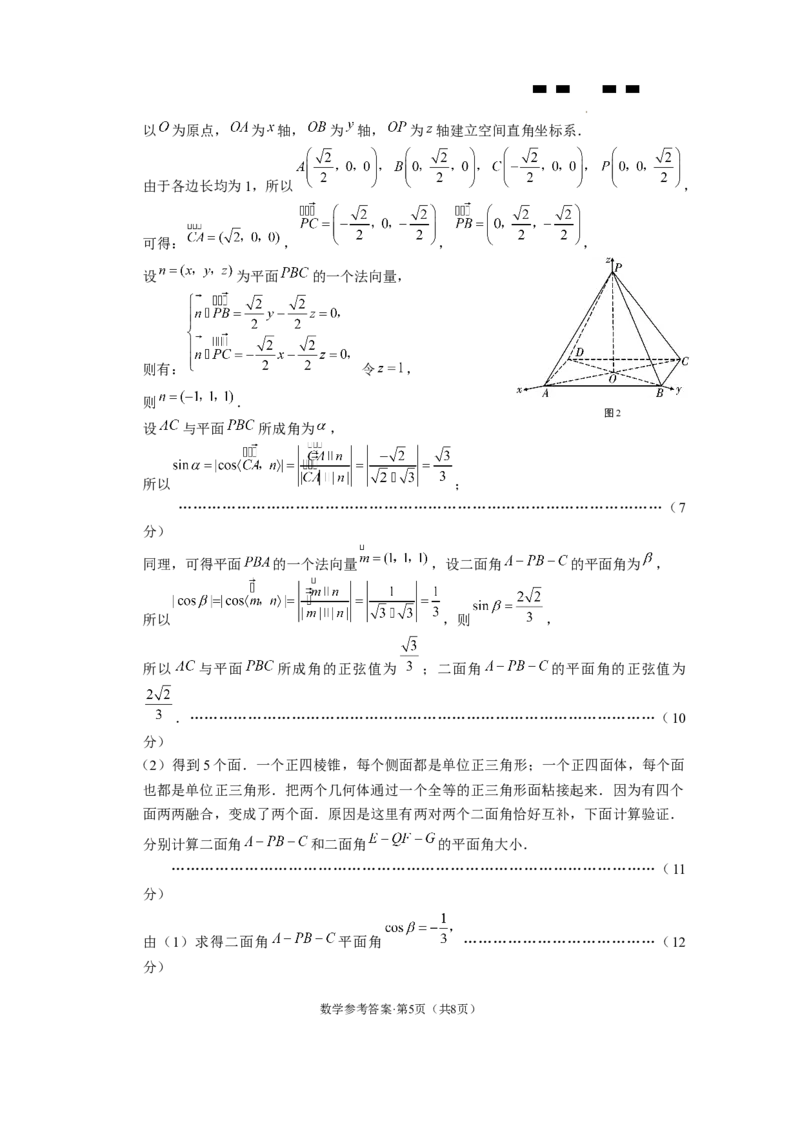
解:(1)如图2,设 ,由正四棱锥的性质, , ,
数学参考答案·第4页(共8页)
学科网(北京)股份有限公司以 为原点, 为 轴, 为 轴, 为 轴建立空间直角坐标系.
由于各边长均为1,所以 ,
可得: , , ,
设 为平面 的一个法向量,
则有: 令 ,
则 .
图2
设 与平面 所成角为 ,
所以 ;
………………………………………………………………………………………(7
分)
同理,可得平面 的一个法向量 ,设二面角 的平面角为 ,
所以 ,则 ,
所以 与平面 所成角的正弦值为 ;二面角 的平面角的正弦值为
.……………………………………………………………………………………(10
分)
(2)得到5个面.一个正四棱锥,每个侧面都是单位正三角形;一个正四面体,每个面
也都是单位正三角形.把两个几何体通过一个全等的正三角形面粘接起来.因为有四个
面两两融合,变成了两个面.原因是这里有两对两个二面角恰好互补,下面计算验证.
分别计算二面角 和二面角 的平面角大小.
………………………………………………………………………………………(11
分)
由(1)求得二面角 平面角 …………………………………(12
分)
数学参考答案·第5页(共8页)
学科网(北京)股份有限公司取 的中点 ,可得 为所求的平面角,
二面角 的平面角 ,
所以 ,这样平面APB与平面QFG融合成了一个平面,
同理:平面DPC与平面QEG融合成了一个平面,
所以组合体有5个面.…………………………………………………………………(15
分)
17.(本小题满分15分)
解:(1)直接法:设点 ,由题意, ,
化简得: .……………………………………………………………(4
分)
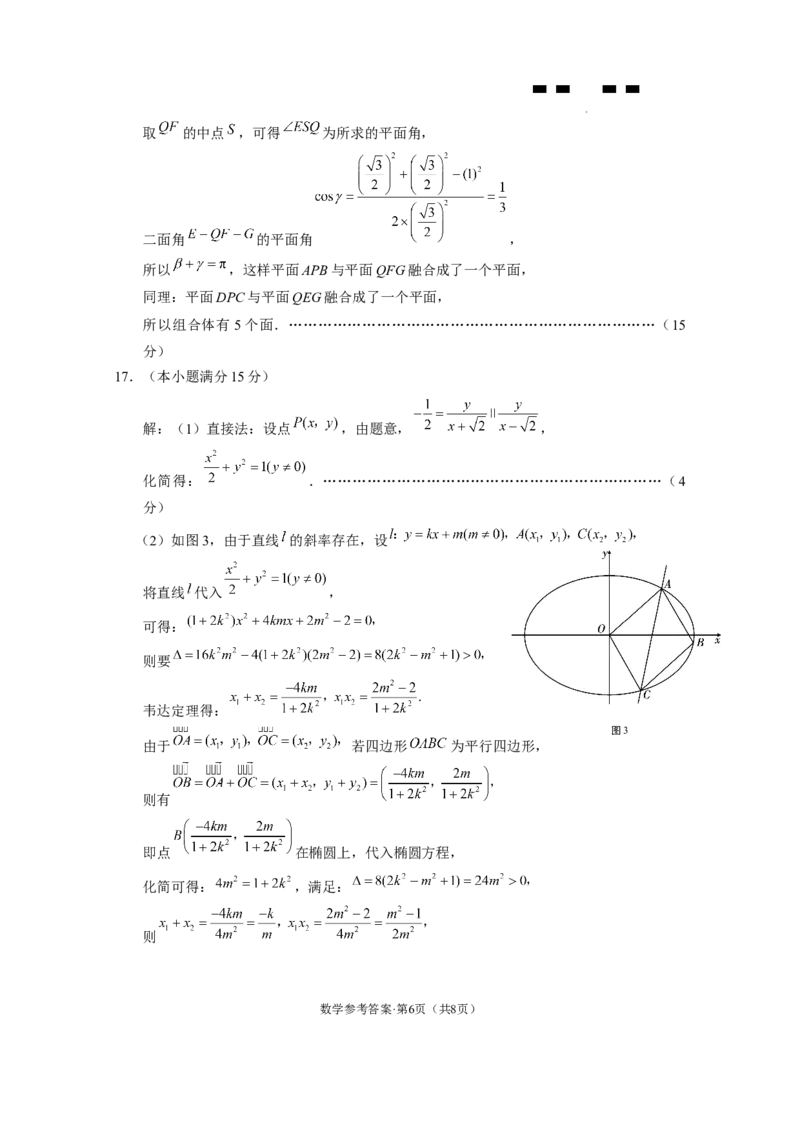
(2)如图3,由于直线 的斜率存在,设
将直线 代入 ,
可得:
则要
韦达定理得:
图3
由于 若四边形 为平行四边形,
则有
即点 在椭圆上,代入椭圆方程,
化简可得: ,满足:
则
数学参考答案·第6页(共8页)
学科网(北京)股份有限公司弦长 ,
点 到直线 的距离 ,
故平行四边形 的面积 ,
所以面积为定值 .…………………………………………………………………(15
分)
18.(本小题满分17分)
解:(1) 的所有可能取值为1,2,3.
1个人的情况为:1号胜胜,则概率为 ,
2 个 人 的 情 况 为 : 1 号 负 2 号 胜 胜 或 1 号 胜 负 2 号 胜 , 概 率 为
,
3个人的概率 ,
所以分布列为:
1 2 3
所以 .…………………………………………………(8
分)
(2)分三种情况:
第一, 一人全胜,该事件的概率设为 ,则
第二, 两人参赛获胜,该事件的概率设为 ,
则
第三, 三人参赛获胜,该事件的概率设为 ,
数学参考答案·第7页(共8页)
学科网(北京)股份有限公司则
由 ,
所以要甲队获胜的概率大于 ,即 ,化简得:
当 ,代入可得: ,成立.………………………………………………(17
分)
19.(本小题满分17分)
(1)解:列举或用公式可求出 .
………………………………………………………………………………………(3
分)
(2)解:由麦克劳林公式,令 ,有
再取 ,可得 ,
所以估算值为 .
在 中,取 ,可得 .
………………………………………………………………………………………(9
分)
(3)证明:由麦克劳林公式,当 时,令 ,有 ,
猜想:
令 ,有 ,猜想:
令 ,由 ,所以 ,即 .
令 , 由 , 所 以 , 即
.
又 时, , ,所以 .
数学参考答案·第8页(共8页)
学科网(北京)股份有限公司令 , 当 ,有 ,
则
命题得证.……………………………………………………………(17
分)
数学参考答案·第9页(共8页)
学科网(北京)股份有限公司