重庆市第八中学2023-2024学年高三下学期高考适应性月考卷（六）数学试题(1)_2024年4月_024月合集_2024届重庆市第八中学高三适应性月考卷（六）

数学试卷 注意事项： 1.答题前，考生务必用黑色碳素笔将自己的姓名､准考证号､考场号､座位号在答题卡上填写清 楚. 2.每小题选出答案后，用 2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦 干净后，再选涂其他答案标号.在试题卷上作答无效， 3.考试结束后，请将本试卷和答题卡一并交回.满分 150分，考试用时 120分钟. 一､单项选择题（本大题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有 一项是符合题目要求的） 1.已知集合M {x∣2 x3},N   x∣x2 5x40  ，则M N （ ） A. 2,1 B. 2,4 C. ,14, D. ,34, 2.已知z1i22i，则 z （ ） 1 A.2 2 B.2 C.1 D. 2 uuur uuur uuur uuur uuur 3.已知BA3,4,BC a,2, AC 2，则ABAC （ ） A.-8 B.8 C.-6 D.6 2x 4.已知 f x 为奇函数，则 f 1（ ） 2ax 1 2 2 A. B. C.2 D.-2 3 3 1 uuur uuur 5.抛物线C: y  x2，过焦点F 的直线l与抛物线C交于A,B两点，若3AF  FB，则直线AB的倾斜 4 角为（ ） A.30o B.60o C.30o或150o D.60o或120o 6.过直线y 2x1上的一点P作圆C:(x2)2 (y5)2 1的两条切线l ,l ，当直线l ,l 关于 1 2 1 2 y 2x1对称时， PC （ ） A.2 2 B.2 3 C.4 D.2 5 a a n 7.已知数列 a  的前n项和为S ，设甲： a  是等差数列，乙：S  1 n ，则甲是乙的（ ） n n n n 2 A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件 学科网（北京）股份有限公司π  10  5π 8.若  ,π ，且cos 3sin ，则sin  2 的值为（ ） 2  13  12 239 2 2 119 2 120 2 A. B. 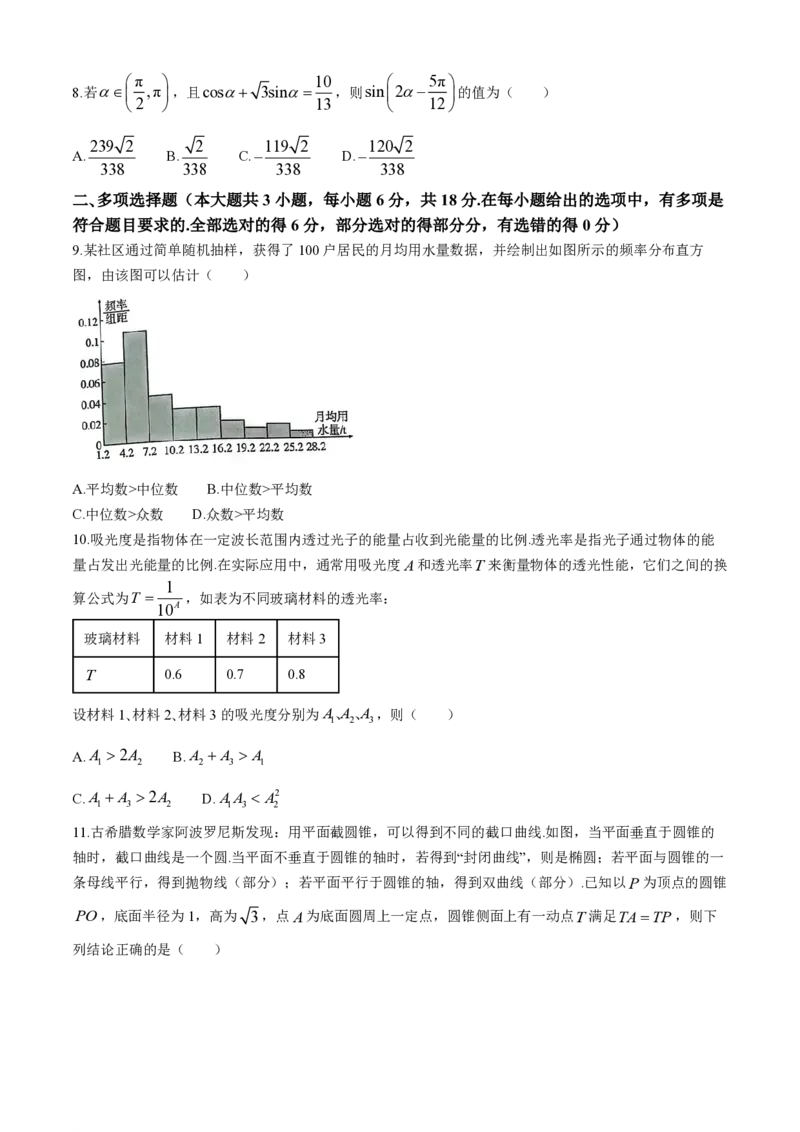C. D. 338 338 338 338 二､多项选择题（本大题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项是 符合题目要求的.全部选对的得 6分，部分选对的得部分分，有选错的得 0分） 9.某社区通过简单随机抽样，获得了100户居民的月均用水量数据，并绘制出如图所示的频率分布直方 图，由该图可以估计（ ） A.平均数>中位数 B.中位数>平均数 C.中位数>众数 D.众数>平均数 10.吸光度是指物体在一定波长范围内透过光子的能量占收到光能量的比例.透光率是指光子通过物体的能 量占发出光能量的比例.在实际应用中，通常用吸光度A和透光率T来衡量物体的透光性能，它们之间的换 1 算公式为T  ，如表为不同玻璃材料的透光率： 10A 玻璃材料 材料1 材料2 材料3 T 0.6 0.7 0.8 设材料1､材料2､材料3的吸光度分别为A､A､A ，则（ ） 1 2 3 A.A 2A B.A  A  A 1 2 2 3 1 C.A  A 2A D.AA  A2 1 3 2 1 3 2 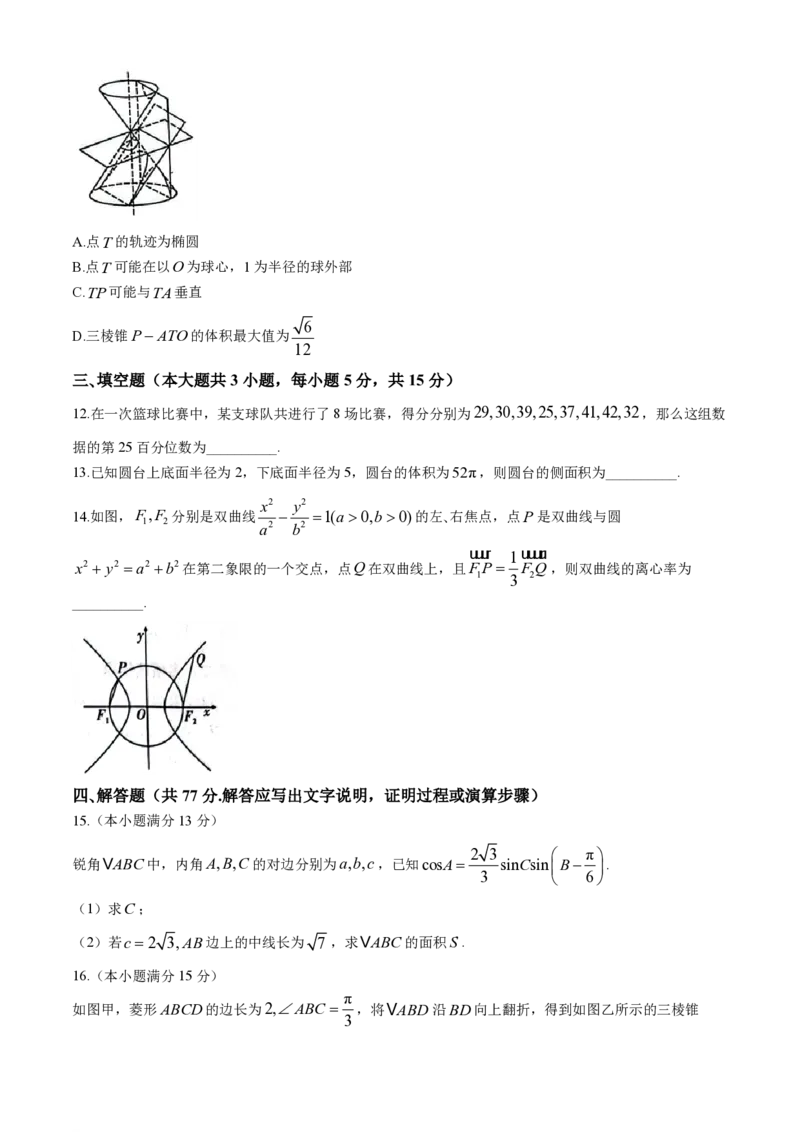11.古希腊数学家阿波罗尼斯发现：用平面截圆锥，可以得到不同的截口曲线.如图，当平面垂直于圆锥的 轴时，截口曲线是一个圆.当平面不垂直于圆锥的轴时，若得到“封闭曲线”，则是椭圆；若平面与圆锥的一 条母线平行，得到抛物线（部分）；若平面平行于圆锥的轴，得到双曲线（部分）.已知以P为顶点的圆锥 PO，底面半径为1，高为 3，点A为底面圆周上一定点，圆锥侧面上有一动点T满足TATP，则下 列结论正确的是（ ） 学科网（北京）股份有限公司A.点T的轨迹为椭圆 B.点T可能在以O为球心，1为半径的球外部 C.TP可能与TA垂直 6 D.三棱锥PATO的体积最大值为 12 三､填空题（本大题共 3小题，每小题 5分，共 15分） 12.在一次篮球比赛中，某支球队共进行了8场比赛，得分分别为29,30,39,25,37,41,42,32，那么这组数 据的第25百分位数为__________. 13.已知圆台上底面半径为2，下底面半径为5，圆台的体积为52π，则圆台的侧面积为__________. 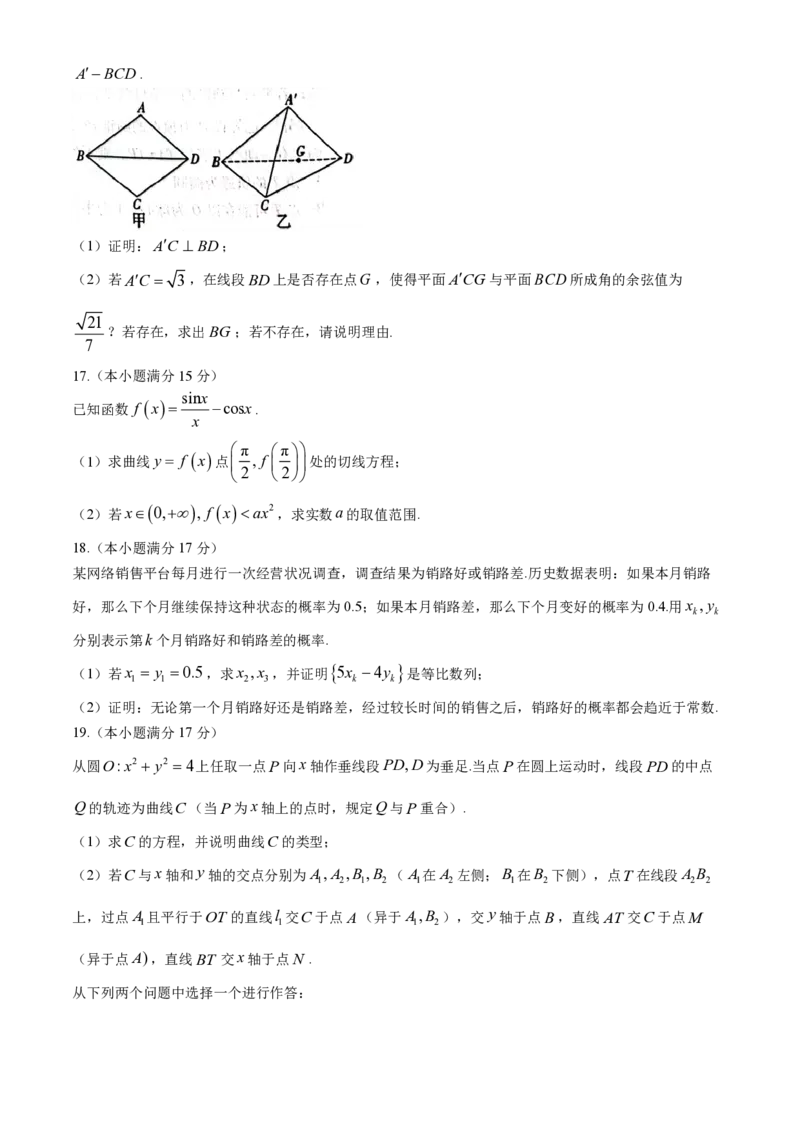x2 y2 14.如图，F,F 分别是双曲线  1(a 0,b0)的左､右焦点，点P是双曲线与圆 1 2 a2 b2 uuur uuuur 1 x2  y2 a2 b2在第二象限的一个交点，点Q在双曲线上，且FP FQ，则双曲线的离心率为 1 3 2 __________. 四､解答题（共 77分.解答应写出文字说明，证明过程或演算步骤） 15.（本小题满分13分） 2 3  π 锐角VABC中，内角A,B,C的对边分别为a,b,c，已知cosA sinCsin  B . 3  6 （1）求C； （2）若c2 3,AB边上的中线长为 7 ，求VABC的面积S. 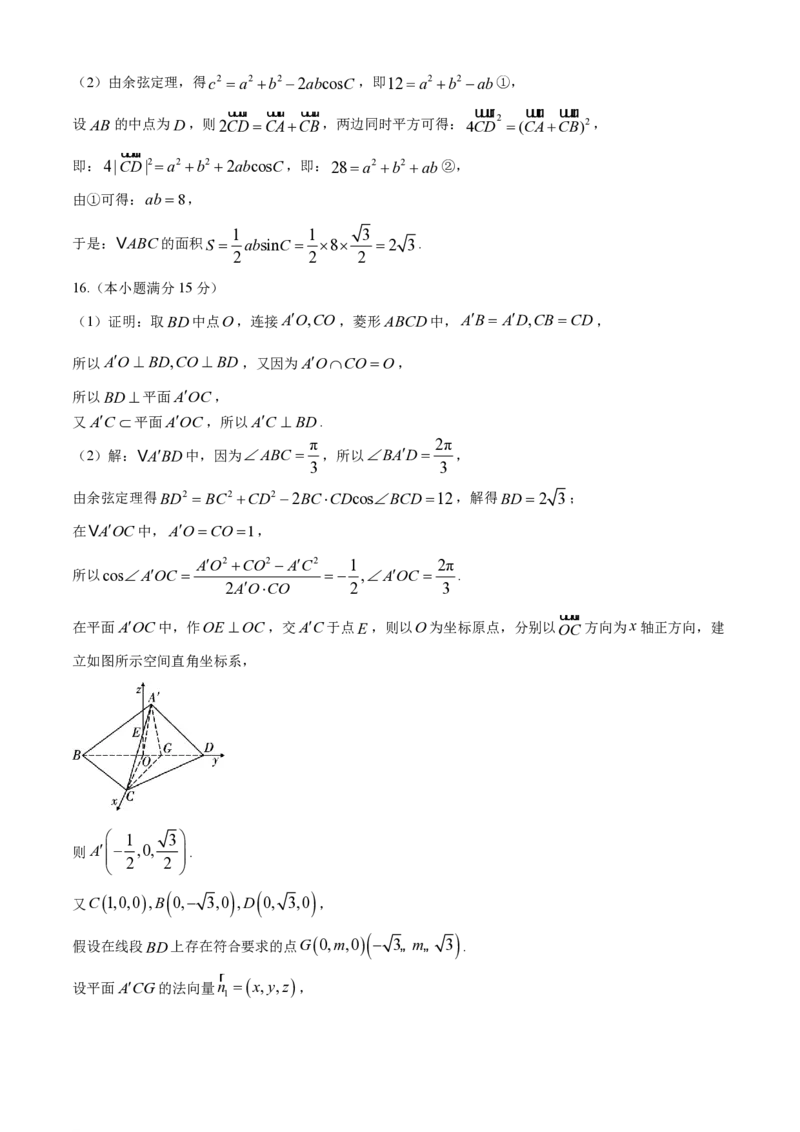16.（本小题满分15分） π 如图甲，菱形ABCD的边长为2,ABC  ，将VABD沿BD向上翻折，得到如图乙所示的三棱锥 3 学科网（北京）股份有限公司ABCD. （1）证明：AC  BD； （2）若AC  3，在线段BD上是否存在点G ，使得平面ACG与平面BCD所成角的余弦值为 21 ？若存在，求出BG；若不存在，请说明理由. 7 17.（本小题满分15分） sinx 已知函数 f x cosx. x π π （1）求曲线y  f x 点 , f  处的切线方程； 2 2 （2）若x0,, f xax2，求实数a的取值范围. 18.（本小题满分17分） 某网络销售平台每月进行一次经营状况调查，调查结果为销路好或销路差.历史数据表明：如果本月销路 好，那么下个月继续保持这种状态的概率为0.5；如果本月销路差，那么下个月变好的概率为0.4.用x ,y k k 分别表示第k个月销路好和销路差的概率. （1）若x  y 0.5，求x ,x ，并证明 5x 4y  是等比数列； 1 1 2 3 k k （2）证明：无论第一个月销路好还是销路差，经过较长时间的销售之后，销路好的概率都会趋近于常数. 19.（本小题满分17分） 从圆O:x2  y2 4上任取一点P向x轴作垂线段PD,D为垂足.当点P在圆上运动时，线段PD的中点 Q的轨迹为曲线C（当P为x轴上的点时，规定Q与P重合）. （1）求C的方程，并说明曲线C的类型； （2）若C与x轴和y轴的交点分别为A,A ,B,B （A在A 左侧；B 在B 下侧），点T在线段A B 1 2 1 2 1 2 1 2 2 2 上，过点A且平行于OT 的直线l 交C于点A（异于A,B ），交y轴于点B，直线AT 交C于点M 1 1 1 2 （异于点A)，直线BT 交x轴于点N . 从下列两个问题中选择一个进行作答： 学科网（北京）股份有限公司①证明： AT  NT  BT  MT ； ②VATN与VBTM 的面积是否相等？请说明理由. 学科网（北京）股份有限公司数学参考答案 一､单项选择题（本大题共 8小题，每小题 5分，共 40分.在每小题给出的四个选项中，只有 一项是符合题目要求的） 题号 1 2 3 4 5 6 7 8 答案 D B B A C D C B 二､多项选择题（本大题共 3小题，每小题 6分，共 18分.在每小题给出的选项中，有多项是 符合题目要求的.全部选对的得 6分，部分选对的得部分分，有选错的得 0分） 题号 9 10 11 答案 AC BCD ACD 三､填空题（本大题共 3小题，每小题 5分，共 15分） 号 12 13 14 10 答案 29.5 35π 2 四､解答题（共 77分.解答应写出文字说明，证明过程或演算步骤） 15.（本小题满分13分） 解：（1）因为AπBC ， 所以cosAcosBCsinBsinCcosBcosC， 2 3  π 2 3  3 1  又cosA sinCsin  B   sinC  sinB cosB  3  6 3  2 2  3 sinBsinC sinCcosB， 3 3 2 3 1 3  所以cosBcosC  sinCcosB，所以 cosB sinC cosC0，   3 3  2 2  1 3 所以cosB0或 sinC cosC 0， 2 2 π 若cosB0，则B  ，与VABC为锐角三角形矛盾，舍去， 2 1 3 从而 sinC cosC 0，则tanC  3， 2 2 π π 又0C  ，所以C  . 2 3 学科网（北京）股份有限公司（2）由余弦定理，得c2 a2 b2 2abcosC，即12a2 b2 ab①， uuur uuur uuur uuur uuur uuur 设AB的中点为D，则2CDCACB，两边同时平方可得：4CD 2 (CACB)2， uuur 即：4|CD|2a2 b2 2abcosC，即：28a2 b2 ab②， 由①可得：ab8， 1 1 3 于是：VABC的面积S  absinC  8 2 3. 2 2 2 16.（本小题满分15分） （1）证明：取BD中点O，连接AO,CO，菱形ABCD中，AB AD,CBCD， 所以AO BD,CO BD，又因为AOCOO， 所以BD平面AOC， 又AC 平面AOC，所以AC  BD. π 2π （2）解：VABD中，因为ABC  ，所以BAD ， 3 3 由余弦定理得BD2  BC2 CD2 2BCCDcosBCD12，解得BD2 3； 在VAOC中，AOCO1， AO2 CO2 AC2 1 2π 所以cosAOC   ,AOC  . 2AOCO 2 3 uuur 在平面AOC中，作OE OC，交AC于点E，则以O为坐标原点，分别以OC方向为x轴正方向，建 立如图所示空间直角坐标系，  1 3 则A ,0, .   2 2       又C1,0,0,B 0, 3,0 ,D 0, 3,0 ，   假设在线段BD上存在符合要求的点G0,m,0  3„ m„ 3 . r 设平面ACG的法向量n x,y,z ， 1 学科网（北京）股份有限公司uuuur 3 3 uuur 由AC  ,0, ,CG 1,m,0 ，   2 2   uuuur r 3 3 ACn  x z 0 r   则 1 2 2 ，取n  m,1, 3m . uuur 1  r CGn xmy 0  1 uur 平面BCD的法向量n 0,0,1； 2 ur uur ur uur n n 3m 21 3 1 2 所以 cos n ,n  ur uur   ,m . 1 2 n  n m2 13m2 7 3 1 2 3 4 3 3 2 3 当m 时，BG  ；当m 时，BG  . 3 3 3 3 4 3 2 3 21 所以当BG  或 时，平面ACG与平面BCD所成角的余弦值为 . 3 3 7 17.（本小题满分15分） xcosxsinx π 4 解：（1） fx sinx, f   1 . x2 2 π2 π 2 因为 f    ， 2 π 2  4  π  4  4 π 所以切线方程为y   1  x ，即y   1  x  . π  π2  2  π2  π 2 （2）由题意，sinxxcosxax3 0. 令gxsinxxcosxax3，则gx xsinx3ax2  xsinx3ax . 令hxsinx3ax,hxcosx3a. 1 ①当3a„ 1，即a„  时，hx…0,hx 在 0, 单调递增，hxh00，所以 3 gx0,gx 在 0, 单调递增，gx g00，不合题意. 1 ②当3a…1，即a… 时，hx„ 0,hx 在 0, 单调递减，hxh00， 3 所以gx0,gx 在 0, 单调递减，所以gx g00，符合题意. 1 1 ③当13a1，即 a 时，由h013a 0,hπ13a0， 3 3 学科网（北京）股份有限公司所以x 0,π ，使得hx 0且x0,x  时，hx0， 0 0 0 所以gx0,gx 在 0,x  单调递增，gx  g00，不符合题意. 0 0 1 综上，a… . 3 18.（本小题满分17分） 解：（1）设事件A “第k个月销路好”，B “第k个月销路差”. k k 由题意，知PA  PA ∣A PA PA ∣B PB  ， k1 k1 k k k1 k k PB  PB ∣A PA PB ∣B PB  . k1 k1 k k k1 k k x 0.5x 0.4y , k1 k k 即： y 0.5x 0.6y  k1 k k 当x  y 0.5时，x 0.5x 0.4y 0.45； 1 1 2 1 1 y 0.5x 0.6y 0.55,x 0.5x 0.4y 0.445 2 1 1 3 2 2 5x 4y 50.5x 0.4y 40.5x 0.6y  k1 k1 k k k k 0.5x 0.4y 0.15x 4y  . k k k k 因为5x 4y 0.5，所以 5x 4y  是首项为0.5，公比为0.1的等比数列. 1 1 k k （2）如果第一个月销路好，则x 1,y 0,5x 4y 5. 1 1 1 1 k1  1  由（1）知，5x 4y 5   . k k 10 5  1  k1 1 2 1  1  k1 所以y k  4   x k   10     .所以x k1  2 x k  5 y k  x k  2   10   . 1  1  k2 1   1  k2  1  k3 从而x  x      x        k k1 2 10 k2 2  10 10  1   1  k2  1  k3  1  k4  x           k3 2  10 10 10  1   1  k2  1  k3  1  k4  4 5  1  k1  x          L 1      . 1 2  10 10 10  9 9 10 k1 4 5  1  即X      k 9 9 10 学科网（北京）股份有限公司如果第一个月销路差，则x 0,y 1,5x 4y 4. 1 1 1 1 k1 4 4  1  同理可得，x      . k 9 9 10 4 可以看到，无论第一个月销路好还是销路差，经过较长时间的销售之后，销路好的概率会趋近于常数 . 9 19.（本小题满分17分） 解：（1）设Qx,y ，则Px,2y ，因为P在圆O上， x2 所以x2 4y2 4，即  y2 1， 4 x2 所以C的方程为  y2 1. 4     C是长轴长为4，焦点为  3,0 , 3,0 的椭圆. （2）先证明BM ∥OT ，且B,N,M 共线. 1 1 x2 由（1）知C:  y2 1，故A 2,0,A 2,0,B 0,1,B 0,1 ， 1 2 1 2 4 直线A B 的方程为x2y20. 2 2 当OT 斜率不存在的时候，直线l 与C仅有一个公共点，不合题意，所以OT 斜率存在， 1 1 设直线OT : y kx，因为当OT ∥ AB 时，A与B 重合，不合题意，所以k  . 1 2 2 2 当OT 斜率为零时，直线BT 与x轴重合，不合题意， 又因为点T在线段A B 上，所以k 0. 2 2 1 综上，k 0，且k  . 2 y kx,  2 2k  由 得T  , ， x2y20. 12k 12k  因为l ∥OT ，所以l : y kx2 ，则B0,2k ， 1 1 1  由k k ，得N  ,0 ， BT BN k  y kx2,  设Ax ,y  ，由x2 得  14k2 x2 16k2x16k2 40， 1 1   y2 20.  4 学科网（北京）股份有限公司16k2 4 28k2 4k 故2x  ，所以x  ,y kx 2 ， 1 14k2 1 14k2 1 1 14k2 28k2 4k  即A , .  14k2 14k2  易得，BN : y kx1，则BN ∥l ，设BN 交C于M x ,y  ， 1 1 1 1 1 2 2 y kx1,  8k 由x2 得  14k2 x2 8kx0，故x  .  y2 1. 2 14k2   4 解法一： 8k 1 4k2 1 M N x x 1 ON TN x x    , 1  2 N    ， 2 N 14k2 k k  14k2 AB x 2k OA TB 1 1 2  4k2 1 2 又 x x x x  0. 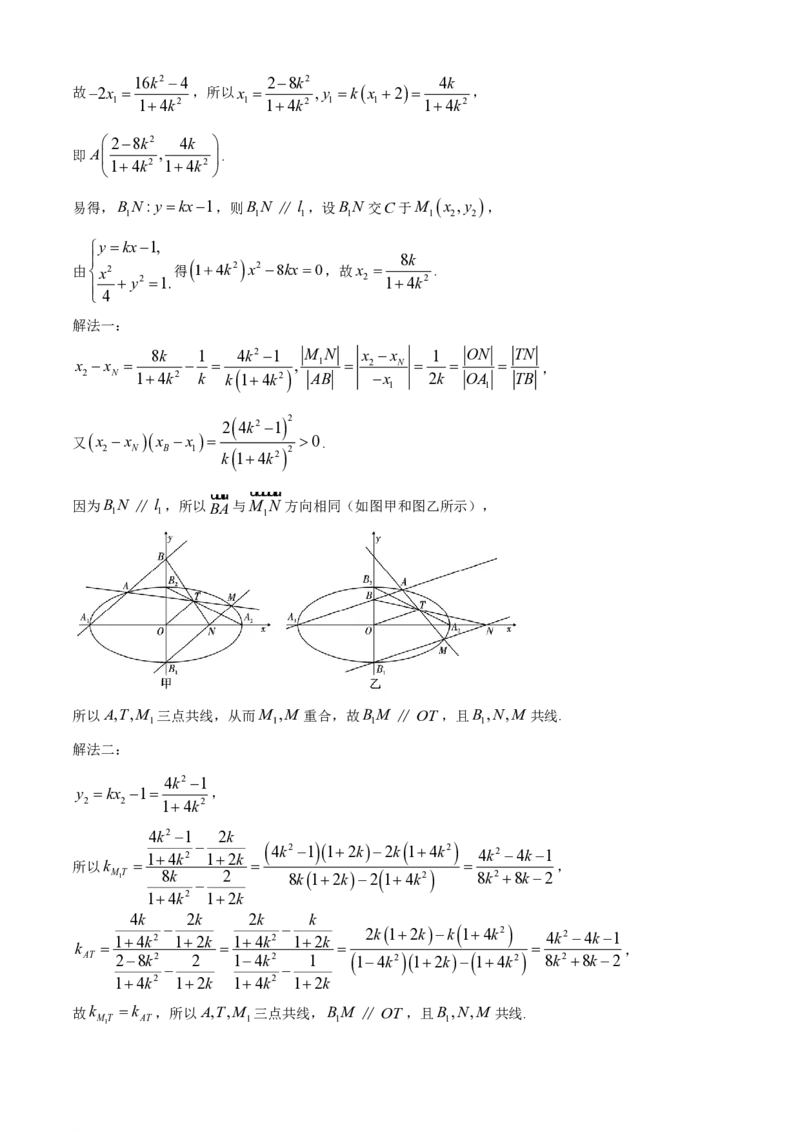2 N B 1 k  14k22 uuur uuuuur 因为BN ∥l ，所以BA与M N 方向相同（如图甲和图乙所示）， 1 1 1 所以A,T,M 三点共线，从而M ,M 重合，故BM ∥OT ，且B,N,M 共线. 1 1 1 1 解法二： 4k2 1 y kx 1 ， 2 2 14k2 4k2 1 2k 14k2  12k  4k2 1 12k2k  14k2 4k2 4k1 所以k    ， M 1 T 8k 2 8k12k2  14k2 8k2 8k2  14k2 12k 4k 2k 2k k 14k2  12k 14k2  12k 2k12kk  14k2 4k2 4k1 k     ， AT 28k2 2 14k2 1  14k212k  14k2 8k2 8k2   14k2 12k 14k2 12k 故k k ，所以A,T,M 三点共线，BM ∥OT ，且B,N,M 共线. M 1 T AT 1 1 1 学科网（北京）股份有限公司1 4k 28k2 因为k 0，且k  ，所以2k  ，（或利用 0） 2 14k2 14k2 所以A,B不重合，A,N,T 不共线. MT TN 若选①，则由BM ∥OT ，且B,N,M 共线，得  ， 1 1 AT TB 即 AT  NT  BT  MT . 若选②，则由BM ∥OT ，且B,N,M 共线，得VABN 与VABM 面积相等， 1 1 所以，VATM 与VBTM 面积相等. 学科网（北京）股份有限公司