文档内容
沈阳二中 2023-2024 学年度上学期高三 10 月(数学)阶段测试
命题人:赵贤忠 校对人:牛大伟
一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
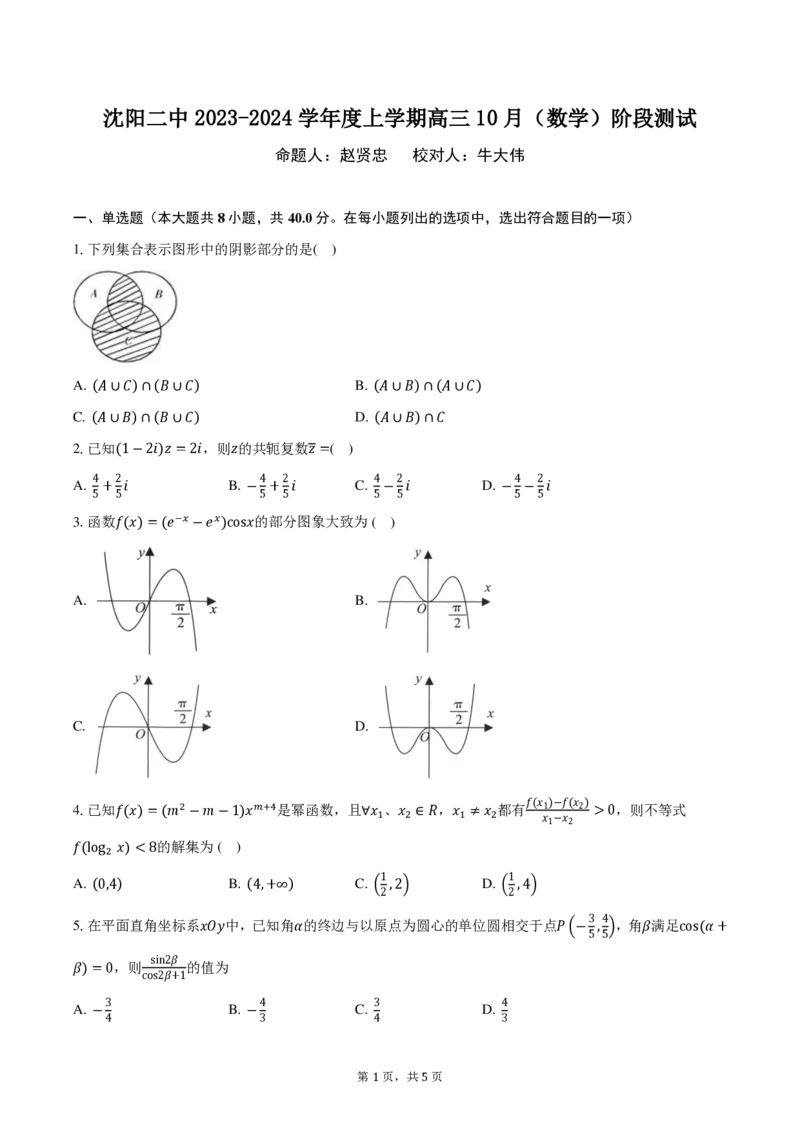
1.下列集合表示图形中的阴影部分的是( )
A. (𝐴∪𝐶)∩(𝐵∪𝐶) B. (𝐴∪𝐵)∩(𝐴∪𝐶)
C. (𝐴∪𝐵)∩(𝐵∪𝐶) D. (𝐴∪𝐵)∩𝐶
2.已知(1−2𝑖)𝑧 =2𝑖,则𝑧的共轭复数𝑧 =( )
4 2 4 2 4 2 4 2
A. + 𝑖 B. − + 𝑖 C. − 𝑖 D. − − 𝑖
5 5 5 5 5 5 5 5
3.函数𝑓(𝑥)=(𝑒−𝑥−𝑒𝑥)cos𝑥的部分图象大致为( )
A. B.
C. D.
𝑓(𝑥 )−𝑓(𝑥 )
4.已知𝑓(𝑥)=(𝑚2−𝑚−1)𝑥𝑚+4是幂函数,且∀𝑥 、𝑥 ∈𝑅,𝑥 ≠𝑥 都有 1 2 >0,则不等式
1 2 1 2 𝑥 −𝑥
1 2
𝑓(log 𝑥)<8的解集为( )
2
1 1
A. (0,4) B. (4,+∞) C. ( ,2) D. ( ,4)
2 2
3 4
5.在平面直角坐标系𝑥𝑂𝑦中,已知角𝛼的终边与以原点为圆心的单位圆相交于点𝑃(− , ),角𝛽满足cos(𝛼+
5 5
sin2𝛽
𝛽)=0,则 的值为
cos2𝛽+1
3 4 3 4
A. − B. − C. D.
4 3 4 3
第1页,共5页
{#{QQABIYwAggggQAAAAAhCAwHwCgGQkACACAoOQBAIsAABQQFABAA=}#}6.勒洛三角形是一种典型的定宽曲线,以等边三角形每个顶点为圆心,以边长为
半径,在另两个顶点间作一段圆弧,三段圆弧围成的曲边三角形就是勒洛三角形
.在如图所示的勒洛三角形中,已知𝐴𝐵 =2,𝑃为弧𝐴𝐶上的点且 ,
则𝐵⃗⃗⃗⃗𝑃⃗ ⋅𝐶⃗⃗⃗⃗𝑃⃗ 的值为( )
A. 4−√ 2 B. 4+√ 2 C. 4−2√ 2 D. 4+2√ 2
7.由华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥(底面是正方形,侧棱长都相等
的四棱锥),其侧面三角形底边上的高与底面正方形边长的比值为√ 5+1,则以该四棱锥的高为边长的正方形
4
面积与该四棱锥的侧面积之比为( )
1 1
A. 2 B. C. D. 4
4 2
8.记𝑎 = 2023√2022,𝑏 = 2023√2023,𝑐 = 2024√2023,则𝑎,𝑏,𝑐的大小关系是( )
A. 𝑎 >𝑏 >𝑐 B. 𝑎 >𝑐 >𝑏 C. 𝑏 >𝑐 >𝑎 D. 𝑏 >𝑎 >𝑐
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
9.下列叙述中正确的是( )
A. 若𝑚−2<𝑥 <𝑚+2是1<𝑥 <3的必要不充分条件,则1<𝑚 <3
B. 若𝑎,𝑏,𝑐均为实数,则“𝑎 >𝑏”是“𝑎𝑐2 >𝑏𝑐2”的必要不充分条件
1
C. 若∃𝑥 ∈[ ,3],使不等式𝑥2−𝑎𝑥+1⩾0成立,则𝑎 ⩽2
2
1
D. “𝑎 >1”是“ <1”的充分不必要条件
𝑎
10.已知复数𝑧 =1+𝑖,则下列说法正确的是( )
A. 𝑧的共轭复数是1−𝑖 B. 𝑧的虚部是𝑖
𝑧
C. =𝑖 D. 若复数𝑧 满足|𝑧 −𝑧|=1,则|𝑧 |的最大值是√ 2+1
𝑧 0 0 0
11.已知圆锥的底面半径为2√ 3,高为2,𝑆为顶点,𝐴,𝐵为底面圆周上两个动点,则下列说法正确的是( )
A. 圆锥的体积为24𝜋
B. 圆锥侧面展开图的圆心角大小为√ 3𝜋
C. 圆锥截面𝑆𝐴𝐵面积的最大值为4√ 3
256𝜋
D. 若圆锥的顶点和底面上所有点都在同一个球面上,则此球的体积为
3
第2页,共5页
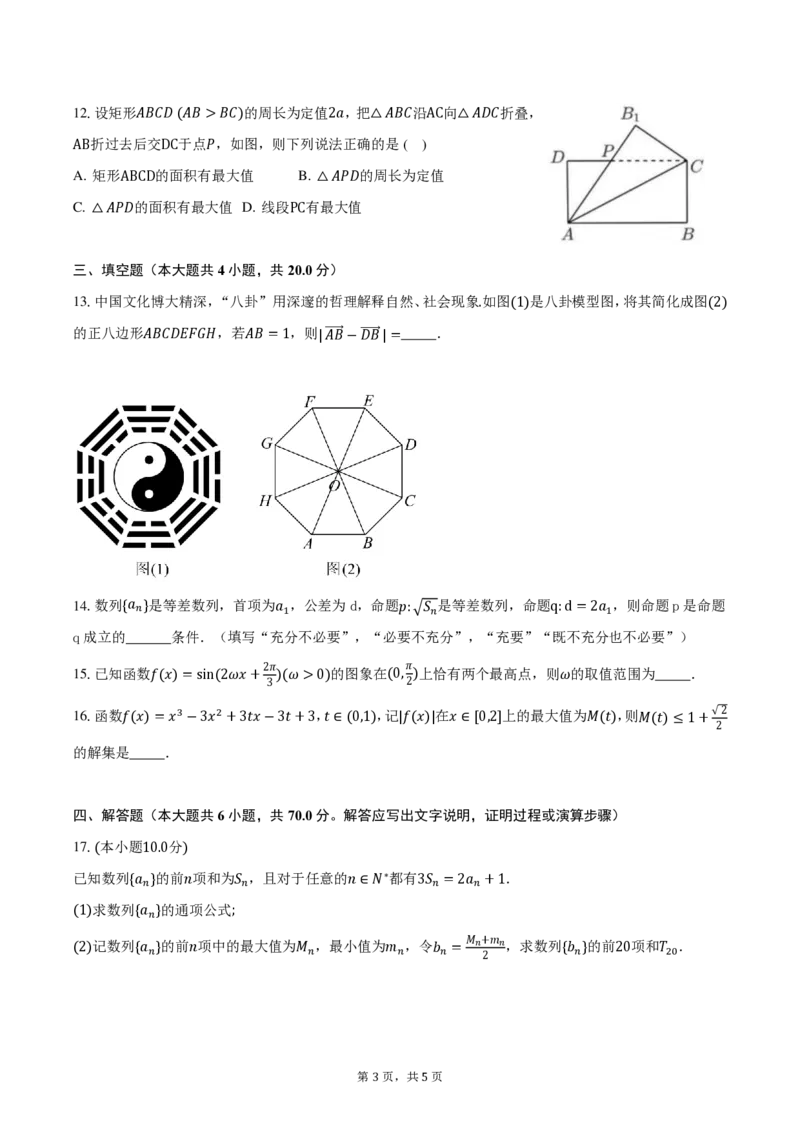
{#{QQABIYwAggggQAAAAAhCAwHwCgGQkACACAoOQBAIsAABQQFABAA=}#}12.设矩形𝐴𝐵𝐶𝐷 (𝐴𝐵 >𝐵𝐶)的周长为定值2𝑎,把△𝐴𝐵𝐶沿AC向△𝐴𝐷𝐶折叠,
AB折过去后交DC于点𝑃,如图,则下列说法正确的是( )
A. 矩形ABCD的面积有最大值 B. △𝐴𝑃𝐷的周长为定值
C. △𝐴𝑃𝐷的面积有最大值 D. 线段PC有最大值
三、填空题(本大题共4小题,共20.0分)
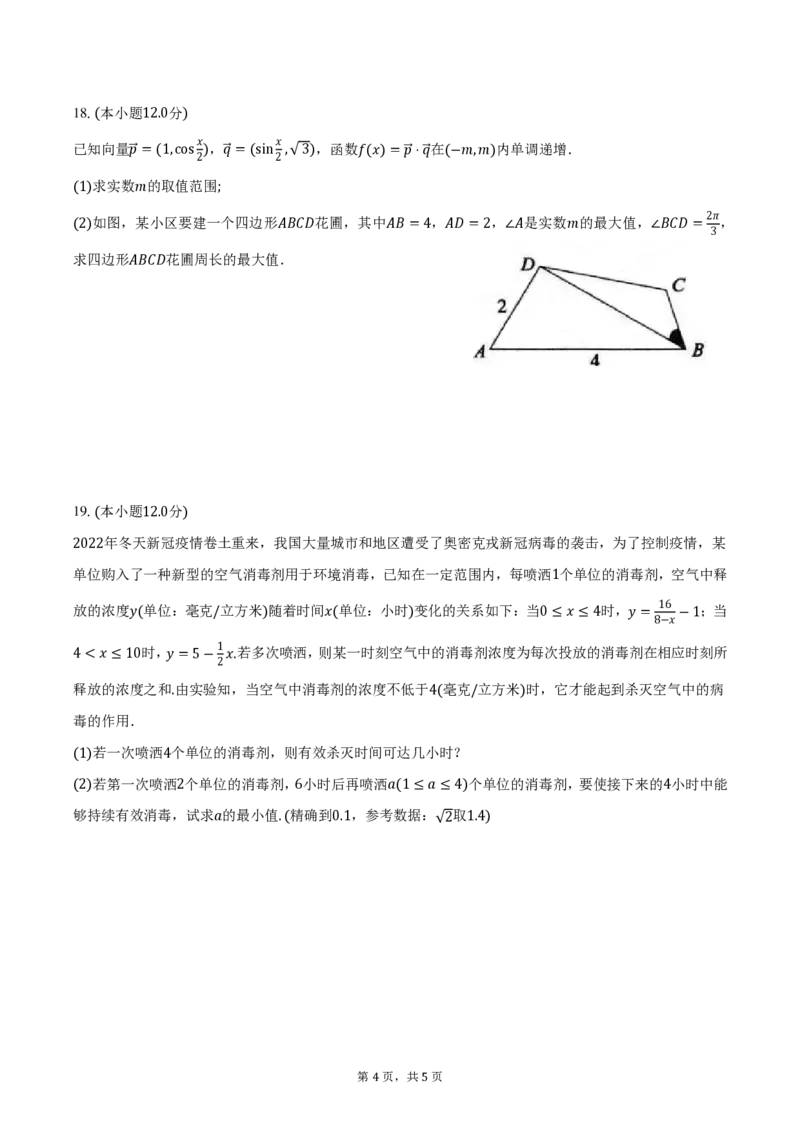
13.中国文化博大精深,“八卦”用深邃的哲理解释自然、社会现象.如图(1)是八卦模型图,将其简化成图(2)
的正八边形𝐴𝐵𝐶𝐷𝐸𝐹𝐺𝐻,若𝐴𝐵 =1,则|𝐴⃗⃗⃗⃗𝐵⃗ −𝐷⃗⃗⃗⃗⃗𝐵⃗ |= .
14.数列{𝑎
𝑛
}是等差数列,首项为𝑎
1
,公差为d,命题𝑝:√𝑆
𝑛
是等差数列,命题q:d=2𝑎
1
,则命题p是命题
q成立的 条件.(填写“充分不必要”,“必要不充分”,“充要”“既不充分也不必要”)
2𝜋 𝜋
15.已知函数𝑓(𝑥)=sin(2𝜔𝑥+ )(𝜔 >0)的图象在(0, )上恰有两个最高点,则𝜔的取值范围为 .
3 2
16.函数𝑓(𝑥)=𝑥3−3𝑥2+3𝑡𝑥−3𝑡+3,𝑡 ∈(0,1),记|𝑓(𝑥)|在𝑥 ∈[0,2]上的最大值为𝑀(𝑡),则𝑀(𝑡)≤1+ √ 2
2
的解集是 .
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17.(本小题10.0分)
已知数列{𝑎 }的前𝑛项和为𝑆 ,且对于任意的𝑛 ∈𝑁∗都有3𝑆 =2𝑎 +1.
𝑛 𝑛 𝑛 𝑛
(1)求数列{𝑎 }的通项公式;
𝑛
(2)记数列{𝑎 }的前𝑛项中的最大值为𝑀 ,最小值为𝑚 ,令𝑏 =
𝑀𝑛+𝑚𝑛,求数列{𝑏
}的前20项和𝑇 .
𝑛 𝑛 𝑛 𝑛 2 𝑛 20
第3页,共5页
{#{QQABIYwAggggQAAAAAhCAwHwCgGQkACACAoOQBAIsAABQQFABAA=}#}18.(本小题12.0分)
𝑥 𝑥
已知向量𝑝⃗⃗ =(1,cos ),𝑞⃗⃗ =(sin ,√ 3),函数𝑓(𝑥)=𝑝⃗⃗ ·𝑞⃗⃗ 在(−𝑚,𝑚)内单调递增.
2 2
(1)求实数𝑚的取值范围;
2𝜋
(2)如图,某小区要建一个四边形𝐴𝐵𝐶𝐷花圃,其中𝐴𝐵 =4,𝐴𝐷 =2,∠𝐴是实数𝑚的最大值,∠𝐵𝐶𝐷 = ,
3
求四边形𝐴𝐵𝐶𝐷花圃周长的最大值.
19.(本小题12.0分)
2022年冬天新冠疫情卷土重来,我国大量城市和地区遭受了奥密克戎新冠病毒的袭击,为了控制疫情,某
单位购入了一种新型的空气消毒剂用于环境消毒,已知在一定范围内,每喷洒1个单位的消毒剂,空气中释
16
放的浓度𝑦(单位:毫克/立方米)随着时间𝑥(单位:小时)变化的关系如下:当0≤𝑥 ≤4时,𝑦 = −1;当
8−𝑥
1
4<𝑥 ≤10时,𝑦 =5− 𝑥.若多次喷洒,则某一时刻空气中的消毒剂浓度为每次投放的消毒剂在相应时刻所
2
释放的浓度之和.由实验知,当空气中消毒剂的浓度不低于4(毫克/立方米)时,它才能起到杀灭空气中的病
毒的作用.
(1)若一次喷洒4个单位的消毒剂,则有效杀灭时间可达几小时?
(2)若第一次喷洒2个单位的消毒剂,6小时后再喷洒𝑎(1≤𝑎 ≤4)个单位的消毒剂,要使接下来的4小时中能
够持续有效消毒,试求𝑎的最小值.(精确到0.1,参考数据:√2取1.4)
第4页,共5页
{#{QQABIYwAggggQAAAAAhCAwHwCgGQkACACAoOQBAIsAABQQFABAA=}#}20.(本小题12.0分)
2𝑏−𝑐 cos𝐶
在△𝐴𝐵𝐶中,角𝐴,𝐵,𝐶所对的边分别为𝑎,𝑏,𝑐.已知𝑎 =3,𝑏 =2, = .
𝑎 cos𝐴
(1)求角𝐴;
(2)求边𝑐;
(3)求cos(3𝐵+𝐶)的值.
21.(本小题12.0分)
已知等差数列{𝑎 }中,𝑎 =2,𝑎 =3(𝑎 −𝑎 ),数列{𝑏 }满足𝑏 =2,𝑏 =2𝑏 .
𝑛 4 5 4 3 𝑛 1 𝑛+1 𝑛
(1)求{𝑎 },{𝑏 }的通项公式;
𝑛 𝑛
−
(3𝑎𝑛+2)(𝑎𝑛−2)
,𝑛为偶数,
(2)任意𝑛 ∈𝑁∗,𝑐 ={ 𝑏𝑛 ,求数列{𝑐 }的前2𝑛项和.
𝑛 𝑎 𝑛
𝑛+2,𝑛为奇数
𝑏𝑛
22.(本小题12.0分)
已知函数𝑓(𝑥)=𝑚𝑒𝑥−1−ln𝑥,𝑚 ∈𝑅.
(1)当𝑚 ≥1时,讨论方程𝑓(𝑥)−1=0解的个数;
(2)当𝑚 =𝑒时,𝑔(𝑥)=𝑓(𝑥)+ln𝑥−
𝑡𝑥2+𝑒有两个极值点𝑥
,𝑥 ,且𝑥 <𝑥 ,若𝑒 <𝑡 <
𝑒2
,
1 2 1 2
2 2
证明:(ⅰ)2<𝑥 +𝑥 <3;
1 2
(ⅱ)𝑔(𝑥 )+2𝑔(𝑥 )<0.
1 2
第5页,共5页
{#{QQABIYwAggggQAAAAAhCAwHwCgGQkACACAoOQBAIsAABQQFABAA=}#}