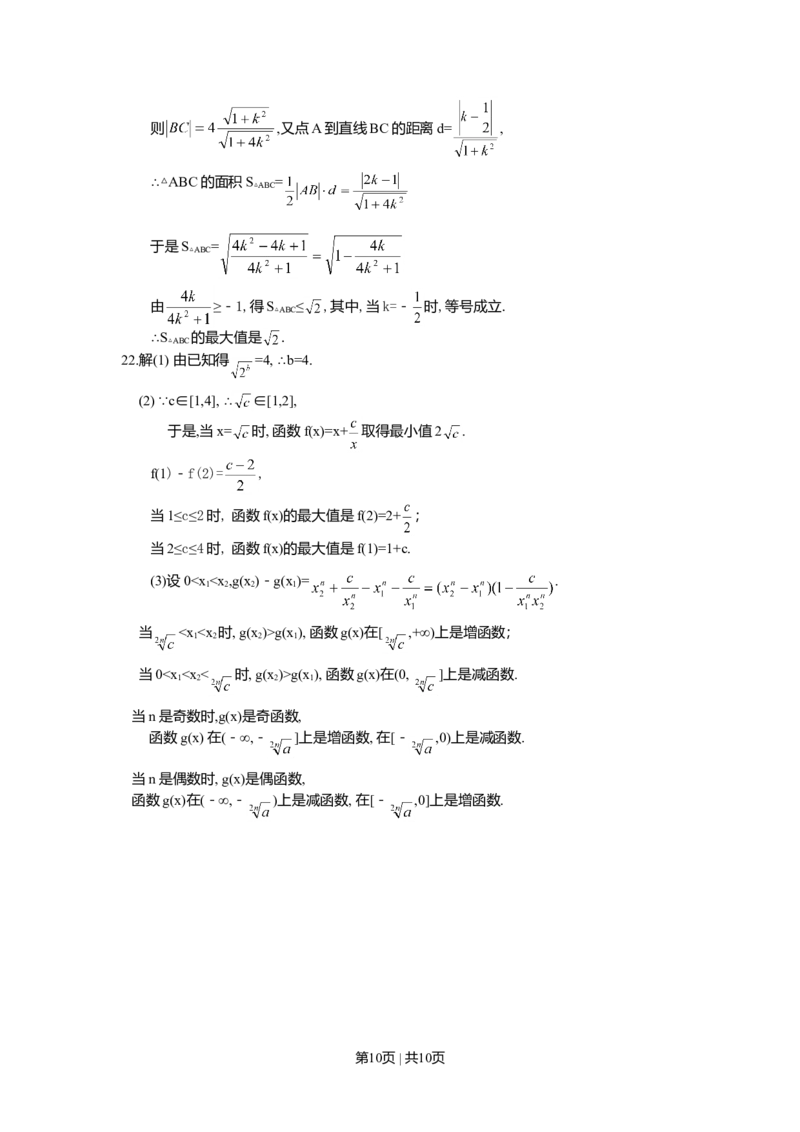文档内容
绝密★启用前
2006 年普通高等学校招生全国统一考试(上海卷)
数学试卷(文史类)
(满分150分,考试时间120分钟)
考生注意
1.本场考试时间120分钟,试卷共4页,满分150分,答题纸共2页.
2.作答前,在答题纸正面填写姓名、准考证号,反面填写姓名,将核对后的条形码贴在答
题纸指定位置.
3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域,不得错位.在试卷上作答一
律不得分.
4.用2B铅笔作答选择题,用黑色字迹钢笔、水笔或圆珠笔作答非选择题.
一、填空题(本大题满分48分)本大题共有12题,只要求直接填写结果,每
个空填对得4分,否则一律得零分。
1、已知 ,集合 ,若 ,则实数 。
2、已知两条直线 若 ,则 ____.
3、若函数 的反函数的图像过点 ,则 。
4、计算: 。
5、若复数 满足 ( 为虚数单位),其中 则 。
6、函数 的最小正周期是_________。
7、已知双曲线中心在原点,一个顶点的坐标为 ,且焦距与虚轴长之比为
,则双曲线的标准方程是____________________.
8、方程 的解是_______.
第1页 | 共10页9、已知实数 满足 ,则 的最大值是_________.
10、在一个小组中有8名女同学和4名男同学,从中任意地挑选 2名同学担任
交通安全宣传志愿者,那么选到的两名都是女同学的概率是______(结果用分
数表示)。
11、若曲线 与直线 没有公共点,则 的取值范围是_________.
12、如图,平面中两条直线 和 相交于点 ,
对于平面上任意一点 ,若 分别是 到直线
和 的距离,则称有序非负实数对 是点
的“距离坐标”,根据上述定义,“距离坐标”
是(1,2)的点的个数是____________.
二、选择题(本大题满分16分)本大题共有4题,每题都给出代号为A、B、
C、D的四个结论,其中有且只有一个结论是正确的,必须把正确结论的代号写
在题后的圆括号内,选对得4分,不选、选错或者选出的代号超过一个(不论
是否都写在圆括号内),一律得零分。
13、如图,在平行四边形 中,下列结论中错误的是 ( )
(A) (B)
(C) (D)
14、如果 ,那么,下列不等式中正确的是( )
(A) (B)
(C) (D)
15、若空间中有两条直线,则“这两条直线为异面直线”是“这两条直线没有公共
点”的 ( )
第2页 | 共10页(A)充分非必要条件 (B)必要非充分条件
(C)充分必要条件 (D)既非充分又非必要条件
16、如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面
对”。在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的
“正交线面对”的个数是
(A)48 (B) 18 (C) 24 (D)36
三、解答题(本大题满分86分)本大题共有6题,解答下列各题必须写出必要
的步骤。
17、(本题满分12分)
已知 是第一象限的角,且 ,求 的值。
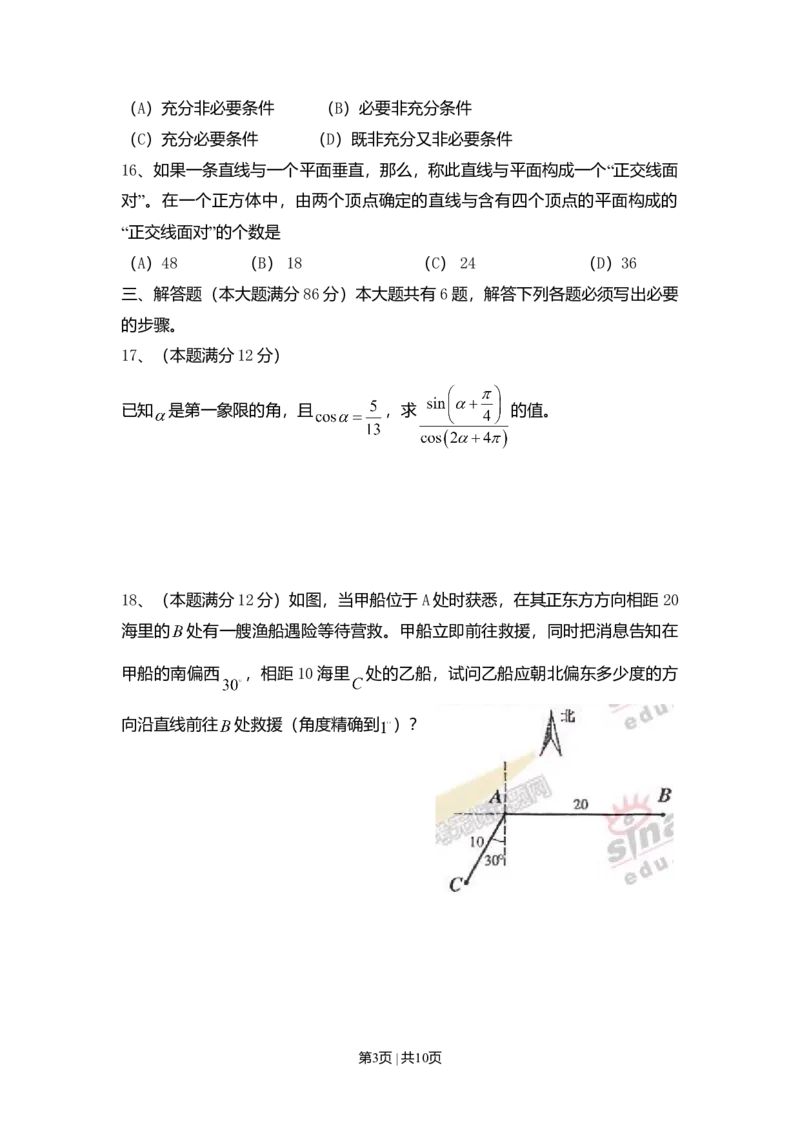
18、(本题满分12分)如图,当甲船位于A处时获悉,在其正东方方向相距20
海里的 处有一艘渔船遇险等待营救。甲船立即前往救援,同时把消息告知在
甲船的南偏西 ,相距10海里 处的乙船,试问乙船应朝北偏东多少度的方
向沿直线前往 处救援(角度精确到 )?
第3页 | 共10页19、(本题满分14)本题共有2个小题,第1小题满分6分,第2小题满分8
分。
在直三棱柱 中, .
(1)求异面直线 与 所成的角的大小;
(2)若 与平面 S所成角为 ,求三棱锥 的体积。
20、(本题满分14)本题共有2个小题,第1小题满分6分,第2小题满分8
分。设数列 的前 项和为 ,且对任意正整数 , 。
(1)求数列 的通项公式
(2)设数列 的前 项和为 ,对数列 ,从第几项起 ?
第4页 | 共10页21、本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分
6分。
已知在平面直角坐标系 中的一个椭圆,它的中心在原点,左焦点为
,右顶点为 ,设点 .
(1)求该椭圆的标准方程;
(2)若 是椭圆上的动点,求线段 中点 的轨迹方程;
(3)过原点 的直线交椭圆于点 ,求 面积的最大值。
22(本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分8
分,第3小题满分6分。
已知函数 有如下性质:如果常数 ,那么该函数在 上是
减函数,在 上是增函数。
(1)如果函数 在 上是减函数,在 上是增函数,求
的值。
(2)设常数 ,求函数 的最大值和最小值;
第5页 | 共10页(3)当 是正整数时,研究函数 的单调性,并说明理由。
第6页 | 共10页上海数学(文史类)参考答案
一、(第1题至笫12题)
1. 4 2. 2 3. 4. 5. 3 6.π 7.
8. 5 9. 0 10. 11.-11,∴ y>1或y<-1,曲线与直线 没有公共点,则 的取值
范围是[-1,1].
12、如图,平面中两条直线 和 相交于点 ,对于平面
上任意一点 ,若 分别是 到直线 和 的距离,
则称有序非负实数对 是点 的“距离坐标”,根据
上述定义,“距离坐标”是(1,2)的点可以在两条直线相
交所成的四个区域内各找到一个,所以满足条件的点的个
数是4个.
二、选择题:
13. C 14. A 15. A 16. D
13.如图,在平行四边形 ABCD 中,根据向量的减法法则知 D C
,所以下列结论中错误的是C.
A B
14、如果 ,那么 ,∴ ,选A.
15、若空间中有两条直线,若“这两条直线为异面直线”,则“这两条直线没有公共点”;若
“这两条直线没有公共点”,则 “这两条直线可能平行,可能为异面直线”;∴ “这两条直线为
异面直线”是“这两条直线没有公共点”的充分非必要条件,选A.
16、如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”.在一
个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”,分情况
讨论:① 对于每一条棱,都可以与两个侧面构成“正交线面对”,这样的“正交线面对”有
2×12=24个;② 对于每一条面对角线,都可以与一个对角面构成“正交线面对”,这样的“正
交线面对”有12个;所以正方体中“正交线面对”共有36个.选D.
三、(第17题至笫22题)
17.解: =
由已知可得sin ,
∴原式= .
18.解:连接BC,由余弦定理得BC2=202+102-2×20×10COS120°=700.
于是,BC=10 .
第8页 | 共10页∵ , ∴sin∠ACB= ,
∵∠ACB<90° ∴∠ACB=41°
∴乙船应朝北偏东71°方向沿直线前往B处救援.
19.解:(1) ∵BC∥B C , ∴∠ACB为异面直线B C 与AC所成角(或它的补角)
1 1 1 1
∵∠ABC=90°, AB=BC=1, ∴∠ACB=45°,
∴异面直线B C 与AC所成角为45°.
1 1
(2) ∵AA ⊥平面ABC,
1
∠ACA 是AC与平面ABC所成的角, ∠ACA =45°.
1 1
∵∠ABC=90°, AB=BC=1, AC= ,
∴AA = .
1
∴三棱锥A-ABC的体积V= S ×AA = .
1 △ABC 1
20.解(1) ∵a + S =4096, ∴a + S =4096, a =2048.
n n 1 1 1
当n≥2时, a = S -S =(4096-a)-(4096-a )= a -a
n n n-1 n n-1 n-1 n
∴ = a=2048( )n-1.
n
(2) ∵log a=log [2048( )n-1]=12-n,
2 n 2
∴T= (-n2+23n).
n
由T<-509,解待n> ,而n是正整数,于是,n≥46.
n
∴从第46项起T<-509.
n
21.解(1)由已知得椭圆的半长轴a=2,半焦距c= ,则半短轴b=1.
又椭圆的焦点在x轴上, ∴椭圆的标准方程为
(2)设线段PA的中点为M(x,y) ,点P的坐标是(x,y),
0 0
x= x=2x-1
0
由 得
y=2y-
y= 0
由,点P在椭圆上,得 ,
∴线段PA中点M的轨迹方程是 .
(3)当直线BC垂直于x轴时,BC=2,因此△ABC的面积S =1.
△ABC
当直线BC不垂直于x轴时,说该直线方程为y=kx,代入 ,
解得B( , ),C(- ,- ),
第9页 | 共10页则 ,又点A到直线BC的距离d= ,
∴△ABC的面积S =
△ABC
于是S =
△ABC
由 ≥-1,得S ≤ ,其中,当k=- 时,等号成立.
△ABC
∴S 的最大值是 .
△ABC
22.解(1) 由已知得 =4, ∴b=4.
(2) ∵c∈[1,4], ∴ ∈[1,2],
于是,当x= 时, 函数f(x)=x+ 取得最小值2 .
f(1)-f(2)= ,
当1≤c≤2时, 函数f(x)的最大值是f(2)=2+ ;
当2≤c≤4时, 函数f(x)的最大值是f(1)=1+c.
(3)设0g(x ), 函数g(x)在[ ,+∞)上是增函数;
1 2 2 1
当0g(x ), 函数g(x)在(0, ]上是减函数.
1 2 2 1
当n是奇数时,g(x)是奇函数,
函数g(x) 在(-∞,- ]上是增函数, 在[- ,0)上是减函数.
当n是偶数时, g(x)是偶函数,
函数g(x)在(-∞,- )上是减函数, 在[- ,0]上是增函数.
第10页 | 共10页