数学（考试版）A3_2024-2025高三（6-6月题库）_2024年06月试卷_学易金卷2024高二期末模拟_高二数学期末模拟卷+人教AB版_683

… … … … … … … … … … … … ○ … ○ … … … … … … … … … … 2023-2024 学年高二数学期末模拟卷 通过，仍可进行第二次面试，若两次均未通过，则面试失败，否则视为面试通过，则该同学通过面试的概 学 校 … … 外 … _____ 内 … 率为（ ） _____ … … … … ____ （考试时间：120分钟 试卷满分：150分） A．0.85 B．0.7 C．0.5 D．0.4 … … … … 姓 名 … … 注意事项： _____ ○ … ○ … 8．已知 为正实数，且满足 ，则 的最小值为（ ） _____ … … … … 1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。答卷前，考生务必将自己的姓名、准考 ___ 班 … … … … 级 ： … … 证号填写在答题卡上。 A． B． C．8 D．6 _____ 装 … 装 … … … _____ … … 2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。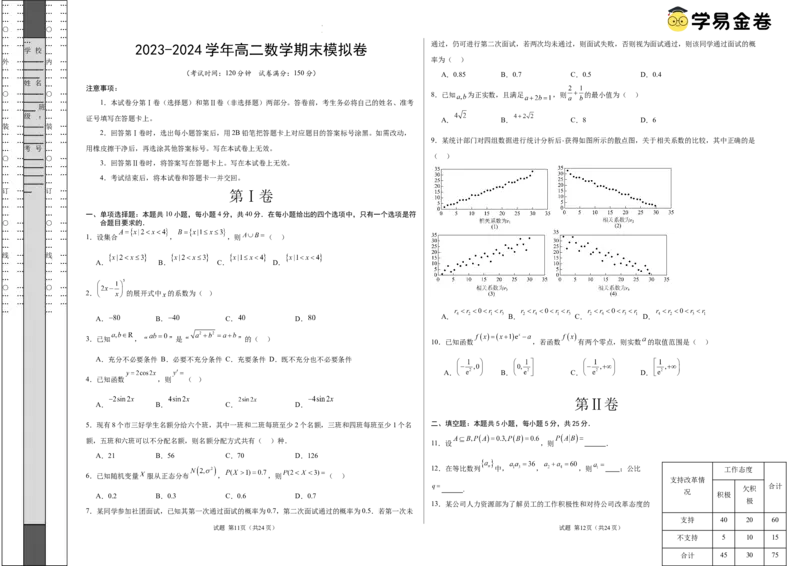如需改动， … …_____ … … 9．某统计部门对四组数据进行统计分析后 获得如图所示的散点图，关于相关系数的比较，其中正确的是 … 考 号 … 用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。 ○ …_____ ○ … （ ） … …_____ … … 3．回答第Ⅱ卷时，将答案写在答题卡上。写在本试卷上无效。 … …_____ … … 4．考试结束后，将本试卷和答题卡一并交回。 … _____ … 订 …__ 订 … 第Ⅰ卷 … … … … … … … … … … 一、单项选择题：本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一个选项是符 ○ … ○ … 合题目要求的． … … … … … … … … 1．设集合 ， ，则 （ ） … … 线 … 线 … … … … … A． B． C． D． … … … … … … ○ … ○ … 2． 的展开式中 的系数为（ ） … … … … … … … … … … A． B． C． D． A． B． C． D． 3．已知 ，“ ”是“ ”的（ ） 10．已知函数 ，若函数 有两个零点，则实数 的取值范围是（ ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 A． B． C． D． 4．已知函数 ，则 （ ） 第Ⅱ卷 A． B． C． D． 5．现有8个市三好学生名额分给六个班，其中一班和二班每班至少2个名额，三班和四班每班至少1个名 二、填空题：本题共5小题，每小题5分，共25分． 额，五班和六班可以不分配名额，则名额分配方式共有（ ）种． 11．设 ，则 ． A．21 B．56 C．70 D．126 12．在等比数列 中， ， ，则 ；公比 工作态度 6．已知随机变量 服从正态分布 ， ，则 （ ） 支持改革情 合计 . 欠积 况 A．0.2 B．0.3 C．0.6 D．0.7 积极 极 13．某公司人力资源部为了解员工的工作积极性和对待公司改革态度的 7．某同学参加社团面试，已知其第一次通过面试的概率为0.7，第二次面试通过的概率为0.5．若第一次未 支持 40 20 60 试题 第11页（共24页） 试题 第12页（共24页） 学学科科网网（（北北京京））股股份份有有限限公公司司 不支持 5 10 15 合计 45 30 75… … … … … … … … … … … … ○ … ○ … … … … … 关系，调查了75名员工，得到以下 列联表： … … … … 此 … … 根据统计结果，认为“平时工作态度积极和支持公司改革有关”犯错误的概率不超过 ． 18．（14分）某高新技术企业新研发出了一种产品， 该产品由三个电子元件构成， 这三个电子元件在 生 卷 内 … 外 … 只 … … … … 装 … … … … 附： ,其中 ． 产过程中的次品率分别为 ，组装过程中不会造成电子元件的损坏，若有 一个电子元件是次品， … 订 … 不 ○ … ○ … 密 … … … … 则该产品为次品. 现安排质检员对这批产品一一检查， 确保无任 何一件次品流入市场. 封 … … … … 0.10 0.05 0.005 0.001 … … (1)若质检员检测出一件次品， 求该产品仅有一个电子元件是次品的概率; 装 … 装 … 2.706 3.841 7.879 10.828 (2)现有两种方案， 方案一: 安排三个质检员先行检测这三个元件， 次品不进入组装生 产线; 方案二: 安 … … … … … … … … 14．高尔顿钉板是英国生物学家高尔顿设计的，如图，每一个黑点表示钉在板上的一颗钉子，上一层的每 排一个质检员检测成品， 一旦发现次品， 则取出重新更换次品的 电子元件， 更换电子元件的费用为 20 … … ○ … ○ … 个钉子的水平位置恰好位于下一层的两颗钉子的正中间，从入口处放进一个直径略小于两颗钉子之间距离 … … … … … … … … 元/个. 已知每个质检员每月的工资约为 3000 元，该企业每月生产该产品 件 ，请从企业获益 的白色圆玻璃球，白色圆玻璃球向下降落的过程中，首先碰到最上面的钉子，碰到 … … 订 … 订 … 钉子后皆以二分之一的概率向左或向右滚下，于是又碰到下一层钉子，如此继续下 的角度选择最优方案. … … … … … … … … 去，直到滚到底板的一个格子内为止．现从入口处放进一个白色圆玻璃球，记白色 … … ○ … ○ … 圆玻璃球落入格子的编号为X，则随机变量X的期望与方差分别为 ， 19．（15分）设 是公比不为1的等比数列， ，再从条件①、条件②这两个条件中选择一个作为已 … … … … … … … … ． … … 知，求： 线 … 线 … 15．若集合A具有以下性质： … … … … … … … … （1）求 的公比； （1）0∈A，1∈A； （2）若x∈A，y∈A；则x﹣y∈ A，且x≠0时， ∈A． … … ○ … ○ … … … … … 则称集合A是“好集”．下列命题中正确的有 （2）求数列 的前 项和． … … … … … … ①．集合B＝{﹣1，0，1}是“好集” ②．有理数集Q是“好集” 条件①： 为 ， 的等差中项；条件②：设数列 的前 项和为 ， . ③．整数集Z不是“好集” ④．设集合A是“好集”，若x∈A，y∈A，则x+y∈A 三、解答题：本题共6小题，共85分．解答应写出文字说明、证明过程或演算步骤． 注：如果选择条件①和条件②分别解答，按第一个解答计分. 16.（13分）袋中装有大小相同的4个红球和6个白球，从中取出4个球． (1)若取出的球必须是两种颜色，则有多少种不同的取法？ (2)若取出的红球个数不少于白球个数，则有多少种不同的取法？ (3)取出一个红球记2分，取出一个白球记1分，若取4球的总分不低于5分，则有多少种不同的取法？ 20．（15分）已知函数 . (1)求函数 的极值； 17．（13分）已知函数 ． (2)若对任意 ，求 的取值范围. (1)求 在 处的切线方程； (2)求 在区间 上的最小值． 21．（15分）设数列 满足：① ；②所有项 ； 试题 第23页（共24页） 试题 第24页（共24页）… … … … … … … … … … … … ○ … ○ … … … … … … … … … … 学 校 ③ ．设集合 ，将集合 中的元素的最小值记为 ．换 … … _____ 外 … 内 … _____ … … … … ____ … … … … 句话说， 是数列 中满足不等式 的所有项的项数的最小值．我们称数列 为数列 的伴随 姓 名 … … _____ ○ … ○ … _____ … … … … 数列．例如，数列1，3，5的伴随数列为1，2，2，3，3． ___ 班 … … … … … 级 ： … (1)请写出数列1，5，7的伴随数列； _____ 装 … 装 … _____ … … … … (2)设 ，求数列 的伴随数列 的前30项之和； … …_____ … … … 考 号 … ○ …_____ ○ … (3)若数列 的前 项和 （其中 常数），求数列 的伴随数列 的前 项和 ． … …_____ … … … …_____ … … … _____ … 订 …__ 订 … … … … … … … … … … … ○ … ○ … … … … … … … … … … … 线 … 线 … … … … … … … … … … … ○ … ○ … … … … … … … … … … … 试题 第31页（共24页） 试题 第32页（共24页） 学学科科网网（（北北京京））股股份份有有限限公公司司