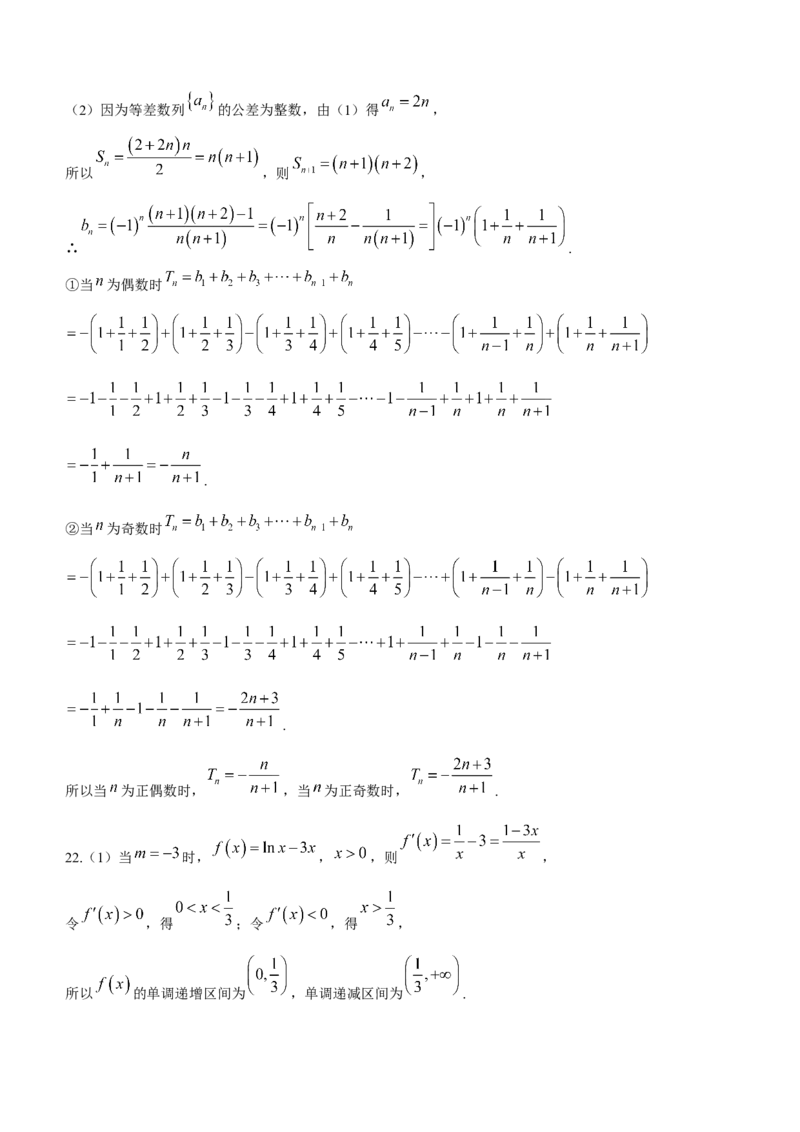文档内容
哈九中 2024 届高三上学期期中考试数学试卷
(考试时间:120分钟 满分:150分)
Ⅰ卷
一、单选题:本题共有8个小题,每小题5分,共40分,在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.已知集合 , ,则 ( )
A. B. C. D.
2.若复数 满足 ,则 的共轭复数的虚部为( )
A. B. C.2 D.
3.在等差数列 中,若 , ,则 ( )
A.29 B.27 C.24 D.20
4.“ , ”是“ ”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
5.下列命题中,真命题的是( )
A.函数 的周期是 B. ,
C.函数 是奇函数 D. 的充要条件是
6.设 , , 是 与 的等差中项,则 的最小值为( )
A. B.3 C.9 D.
7.已知 中, , ,点 为 的中点,点 为边 上一动点,则
的最小值为( )
A.27 B.0 C. D.
8.在流行病学中,基本传染数 是指在没有外力介入,同时所有人都没有免疫力的情况下,一个感染者平均
学科网(北京)股份有限公司传染的人数. 一般由疾病的感染周期、感染者与其他人的接触频率、每次接触过程中传染的概率决定.对于
,而且死亡率较高的传染病,一般要隔离感染者,以控制传染源,切断传播途径.假设某种传染病的基
本传染数 ,平均感染周期为7天(初始感染者传染 个人为第一轮传染,经过一个周期后这 个人
每人再传染 个人为第二轮传染……)那么感染人数这由1个初始感染者增加到1000人大约需要的天数为
(参考数据: , )( )
A.35 B.42 C.49 D.56
二、多选题:本题共4个小题,每小题5分,共20分,在每小题给出的选项中,有多项符合题
目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.
9.数列 满足: , , ,下列说法正确的是( )
A.数列 为等比数列 B.
C.数列 是递减数列 D. 的前 项和
10.下列说法正确的是( )
A.在 中, , , ,若 ,则 为锐角三角形
B.非零向量 和 满足 , ,则
C.已知 , ,且 与 的夹角为锐角,则实数 的取值范围是
D.在 中,若 ,则 与 的面积之比为
11.已知函数 ,则( )
A.若 ,则 B.若函数 为偶函数,则
C.若 在 上单调,则 D.若 时,且 在 上单调,则
学科网(北京)股份有限公司12.已知 ,若 恒成立,则不正确的是( )
A. 的单调递增区间为
B.方程 可能有三个实数根
C.若函数 在 处的切线经过原点,则
D.过 图象上任何一点,最多可作函数 的8条切线
Ⅱ卷
三、填空题:本题共有4个小题,每小题5分,共20分.
13.已知数列 的前 项和为 ,且 ,则数列 的通项公式 ______.
14.已知 的面积 , ,则 ______.
15.若 ,则 ______.
16. , 为一个有序实数组, 表示把 中每个
都变成 ,0,每个0都变成 ,1,每个1都变成0,1所得到的新的有序实数组.例如: ,则
.定义 , ,若 , 中有 项为1, 的
前 项和为 ,则 ______.
四、解答题:本题共有6个小题,共70分.
17.设向量 , ,
(1)若 ,求 的值;
(2)设函数 ,求 的最大值.
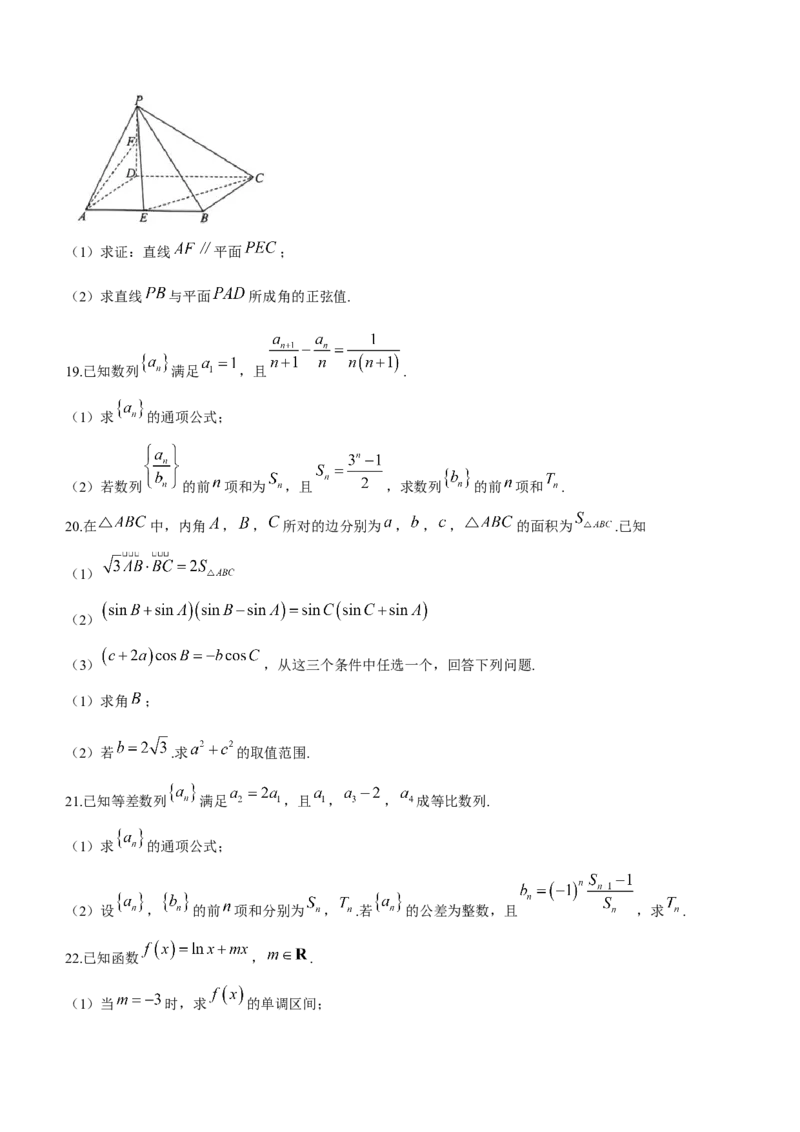
18.如图,在四棱锥 中,底面 是菱形, , 平面 ,
,且点 , 分别为 和 中点.
学科网(北京)股份有限公司(1)求证:直线 平面 ;
(2)求直线 与平面 所成角的正弦值.
19.已知数列 满足 ,且 .
(1)求 的通项公式;
(2)若数列 的前 项和为 ,且 ,求数列 的前 项和 .
20.在 中,内角 , , 所对的边分别为 , , , 的面积为 .已知
(1)
(2)
(3) ,从这三个条件中任选一个,回答下列问题.
(1)求角 ;
(2)若 .求 的取值范围.
21.已知等差数列 满足 ,且 , , 成等比数列.
(1)求 的通项公式;
(2)设 , 的前 项和分别为 , .若 的公差为整数,且 ,求 .
22.已知函数 , .
(1)当 时,求 的单调区间;
学科网(北京)股份有限公司(2)当 时,若不等式 恒成立,求 的取值范围;
(3)证明: .
1——8 DCAACCDB
9——12 AB BD BD ABC
13. 14.2 15. 16.
17.(1)∵ , , ,
∴ ,即 ,得 ,
又∵ ,则 ,∴ ,解得 .
(2)
∵ ,则 ,∴ ,当 取得
18.(1)证明:取 的中点 ,连接 、 ,
在 中,因为 , 分别为 , 的中点,可得 且 ,
又因为 为 的中点,所以 且 ,
所以 且 ,所以四边形 为平行四边形,所以 ,
因为 平面 , 平面 ,所以 平面 .
(2)解:因为底面 是菱形,且 ,连接 ,可得 为等边三角形,
又因为 为 的中点,所以 ,则 ,
又由 平面 ,以 为坐标原点,以 , , 所在的直线分别为 、 和 轴建立空间
直角坐标系,如图所示,
因为底面 是菱形,且 , ,
学科网(北京)股份有限公司可得 , , , ,
则 , , ,
设平面 的法向量为 ,则
取 ,可得 , .所以 ,设直线 与平面 所成的角为 ,
则 ,所以直线 与平面 所成角的正弦值为 .
19.(1)因为 ,
所以
,所以 .
(2)因为 ,所以当 时, ,得 ;
当 时, ,所以 ( 时也成立).
因为 ,所以 ,
学科网(北京)股份有限公司所以
,故 .
20.(1)选①,由 可得:
,故有 ,又∵ ,∴ ;
选②,∵ ,
由正余弦定理得 ,∴ ,又 ,∴ ;
选③,∵ ,由正弦定理可得 ,
∴ ,
∵ ,∴ ,∴ ,又 ,∴ .
(2)由余弦定理得 ∵ ,∴ .
又有 ,当且仅当 时取等号,
可得 .即 的取值范围是 .
21.(1)设等差数列 的公差为 ,∵ ,∴ ,
∵ , , 成等比,∴ ,
即 ,得 ,解得 或 ,
∴当 时, ;当 时, ;∴ 或 .
学科网(北京)股份有限公司(2)因为等差数列 的公差为整数,由(1)得 ,
所以 ,则 ,
∴ .
①当 为偶数时
.
②当 为奇数时
.
所以当 为正偶数时, ,当 为正奇数时, .
22.(1)当 时, , ,则 ,
令 ,得 ;令 ,得 ,
所以 的单调递增区间为 ,单调递减区间为 .
学科网(北京)股份有限公司(2)由 ,得 ,设 , ,
当 时, , ,所以当 时, ,不符合题意,
当 时, ,设 , ,
其图象为开口向下的抛物线,对称轴为 ,当 ,即 时,
因为 ,所以当 时, ,即 ,
此时 单调递增,所以 ,不符合题意.
当 ,即 时, 在 上单调递减,所以 ,
所以 ,所以 在 上单调递减,所以 ,符合题意.
综上所述, 的取值范围为 .
(3)由(2)可得当 时, ,即 ,
令 , ,则 ,
所以 , ,…, ,
以上各式相加得 ,
即 ,
所以 .
学科网(北京)股份有限公司