2006年贵州高考文科数学真题及答案_数学高考真题试卷_旧1990-2007·高考数学真题_1990-2007·高考数学真题·PDF_贵州

2006 年贵州高考文科数学真题及答案 本试卷分第Ｉ卷（选择题）和第Ⅱ卷（非选择题）两部分。第Ｉ卷１至２页。第Ⅱ卷３ 至４页。考试结束后，将本试卷和答题卡一并交回。 第Ｉ卷（选择题） 注意事项： １．答题前，考生在答题卡上务必用黑色签字笔将自己的姓名、准考号填写清楚，并贴 好条形码。请认真核准条形码上的准考证号、姓名和科目。 ２．每小题选出答案后，用２Ｂ铅笔把答题卡上对应题目的答案标号涂黑，如需改动， 用橡皮擦干净后，再选涂其他答案标号，在试题卷上作答无效。 ３．本卷共１２小题，每小题５分，共６０分。在每小题给出的四个选项中，只有一项 是符合题目要求的。 参考公式 如果事件Ａ、Ｂ互斥，那么 球的表面积公式 P(AB) P(A)P(B) S 4R2 如果事件Ａ、Ｂ相互独立，那么 其中R表示球的半径 P(A.B) P(A).P(B) 4 球的体积公式V  R3 3 如果事件Ａ在一次试验中发生的概率是Ｐ，那么 其中R表示球的半径 n k 次独立重复试验中恰好发生 次的概率是 P (k)CkPk(1P)nk n n 一．选择题     (1)已知向量a＝（4，2），向量b＝（x，3），且a//b,则x＝ （A）9 (B)6 (C)5 (D)3 M {x|x3},N x|log x1 M N  （2）已知集合 2 ，则  x|0 x3  （A） （B） x|1 x3 x|2 x3 （C） （D） y sin2xcos2x （3）函数 的最小正周期是   （A） 2 （B） 4 （C） 4 （D） 2 y  f(x) y  f(x) (4）如果函数 的图像与函数y32x的图像关于坐标原点对称，则 的 表达式为 （A）y 2x3 （B）y 2x3 第1页 | 共12页（C）y 2x3 （D）y 2x3 x2  y2 1 ABC 3 （5）已知 的顶点B、C在椭圆 上，顶点A是椭圆的一个焦点，且椭圆的另 ABC 外一个焦点在BC边上，则 的周长是 2 3 4 3 （A） （B）6 （C） （D）12 （6）已知等差数列a 中，a 7,a 15，则前10项的和S ＝ n 2 4 10 （A）100 (B)210 (C)380 (D)400  （7）如图，平面  平面  ， A,B,AB 与两平面  、  所成的角分别为 4  A  B' B  和 6 。过A、B分别作两平面交线的垂线，垂足为A'、 B', 若AB=12,则A'B' A' （A）4 （B）6 （C）8 （D）9 （8）已知函数 f(x)lnx1(x0)，则 f(x)的反函数为 y ex1(xR) y ex1(xR) （A） （B） y ex1(x1) y ex1(x1) （C） （D） x2 y2 4  1 y  x （9）已知双曲线 a2 b2 的一条渐近线方程为 3 ，则双曲线的离心率为 5 4 5 3 （A）3 （B）3 （C）4 （D）2 f(sinx)3cos2x, f(cosx) （10）若 则 3cos2x 3sin2x （A） （B） 3cos2x 3sin2x （C） （D） （11）过点（－1，0）作抛物线y  x2 x1的切线，则其中一条切线为 （A）2x y20 （B）3x y30 （C）x y10 （D）x y10 （12）5名志愿者分到3所学校支教，每个学校至少去一名志愿者，则不同的分派方法共有 （A）150种 (B)180种 (C)200种 (D)280种 第2页 | 共12页第Ⅱ卷（非选择题，共90分） 注意事项： 本卷共2页，10小题，用黑碳素笔将答案答在答题卡上。答在试卷上的答案无效。 二．填空题：本大题共４小题，每小题４分，共１６分，把答案填在横线上。 1 (x4  )10 （13）在 x 的展开式中常数项是＿＿＿＿＿。（用数字作答） （14）圆o 是以 R为半径的球O的小圆，若圆o 的面积S 和球O的表面积 S 的比为 1 1 1 S :S 2:9，则圆心o 到球心O的距离与球半径的比OO :R＿＿＿＿＿。 1 1 1 (1, 2) l (x2)2  y2 4 （15）过点 的直线 将圆 分成两段弧，当劣弧所对的圆心角最小时， l k  ____. 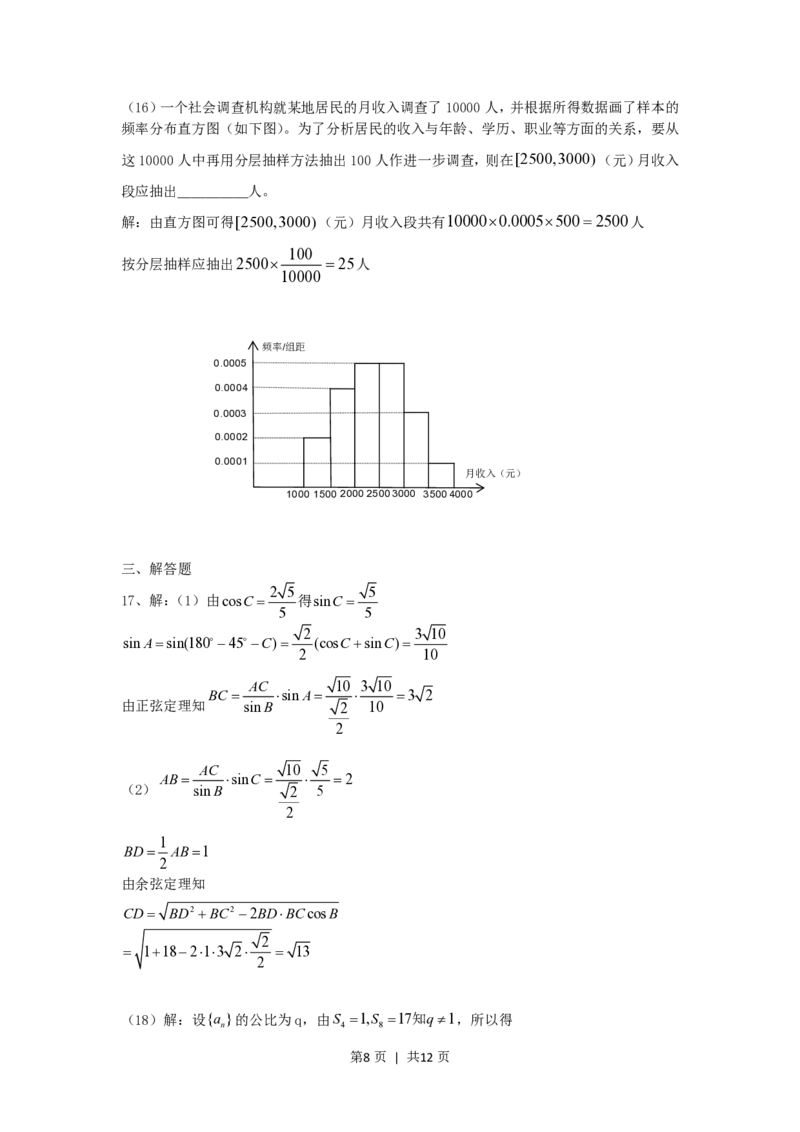直线 的斜率 （16）一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的 频率分布直方图（如下图）。为了分析居民的收入与年龄、学历、职业等方面的关系，要从 [2500,3000) 这10000人中再用分层抽样方法抽出100人作进一步调查，则在 （元）月收入段 应抽出＿＿＿＿＿人。 频率/组距 0.0005 0.0004 0.0003 0.0002 0.0001 月收入（元） 10001500200025003000 35004000 三．解答题：本大题共６小题，共７４分。解答应写出文字说明，证明过程或演算步骤。 （17）（本小题满分１２分） 2 5 在ABC中，B45,AC  10,cosC  ,求 5 （1）BC ? (2)若点D是AB的中点，求中线CD的长度。 （18）（本小题满分１２分） 设等比数列a 的前n项和为S ，S 1,S 17,求通项公式a ? n n 4 8 n （19）（本小题满分１２分） 某批产品成箱包装，每箱5件，一用户在购进该批产品前先取出3箱，再从每箱中任意出 第3页 | 共12页取2件产品进行检验。设取出的第一、二、三箱中分别有0件、1件、2件二等品，其余为一等 品。 （I）求取6件产品中有1件产品是二等品的概率。 （II）若抽检的6件产品中有2件或2件以上二等品，用户就拒绝购买这批产品，求这批 产品被用户拒绝的概率。 （20）（本小题１２分） C 1 B 1 如图，在直三棱柱 ABCA 1 B 1 C 1中， AB BC,D 、E分别为 BB 1、 A 1 AC D 1的中点。 E BB AC （I）证明：ED为异面直线 1与 1的公垂线； C B AA  AC  2AB, A ADC A （II）设 1 求二面角 1 1的大小 (21）（本小题满分为１４分） 设 aR， 函 数 f(x)ax2 2x2a.若 f(x)0的 解 集 为 A ， Bx|1 x3,A B，求实数 a 的取值范围。  （22）（本小题满分１２分）   x2 4y AF FB(0). 已知抛物线 的焦点为F，A、B是热线上的两动点，且 过A、B 两点分别作抛物线的切线，设其交点为M。   （I）证明FM AB为定值；  （II）设ABM 的面积为S，写出 S  f() 的表达式，并求S的最小值。 2006年贵州高考文科数学真题参考答案 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B D D D C B B B A C D A 二、填空题 1 2 （13）45；（14） ；（15） ；（16）25 3 2 一．选择题     （1）已知向量a＝（4，2），向量b＝（x，3），且a//b,则x＝( B ) 第4页 | 共12页（A）9 (B)6 (C)5 (D)3   解：a//b4×3－2x＝0，解得x＝6，选B （2）已知集合M {x|x3},N x|log x1 ，则M N ( D ) 2  （A） （B） x|0 x3 （C） x|1 x3 （D） x|2 x3     解：N  x log x1  x x2 ,用数轴表示可得答案D 2 （3）函数y sin2xcos2x的最小正周期是(D )   （A）2 （B）4 （C） （D） 4 2 1 2  解析: y sin2xcos2x sin4x所以最小正周期为T   ,故选D 2 4 2 （4）如果函数 y  f(x)的图像与函数 y32x的图像关于坐标原点对称，则 y  f(x) 的表达式为( D ) （A）y 2x3 （B）y 2x3 （C）y 2x3 （D）y 2x3 解：以－y，－x代替函数y32x中的x，y，得 y  f(x)的表达式为y 2x3 ，选D x2 （5）已知ABC的顶点B、C在椭圆  y2 1上，顶点A是椭圆的一个焦点，且椭圆的 3 另外一个焦点在BC边上，则ABC的周长是( C ) （A）2 3 （B）6 （C）4 3 （D）12 解：(数形结合)由椭圆的定义椭圆上一点到两焦点的距离之和等于长轴长2a,可得ABC的 周长为4a=4 3,所以选C （6）已知等差数列 a  中，a 7,a 15，则前10项的和S ＝(B ) n 2 4 10 （A）100 (B)210 (C)380 (D)400 a a 157 解：d＝ 4 2  4，a ＝3，所以 S ＝210，选B 42 2 1 10 （7）如图，平面平面，A,B,AB与两平面、所成    A 的角分别为 和 。过A、B 分别作两平面交线的垂线，垂足为A'、 4 6 B' B  A' 第5页 | 共12页B',若AB=12,则A'B'( A ) （A）4 （B）6 （C）8 （D）9  解 ： 连 接 AB和AB, 设 AB=a, 可 得 AB 与 平 面 所 成 的 角 为 BAB , 在 4 2  Rt BAB中有AB a,同理可得 AB 与平面 所成的角为 ABA ,所以  2 6 1 2 1 1 AA a, 因 此 在 Rt AAB中AB ( a)2 ( a)2  a, 所 以  2 2 2 2 1 AB:A'B'a: a2:1,故选A 2 （8）已知函数 f(x)lnx1(x0)，则 f(x)的反函数为(B ) （A）y ex1(xR) （B）y ex1(xR) （C）y ex1(x1) （D）y ex1(x1) 解： y lnx1(x0)lnx y1 xey1(yR)所以反函数为 y ex1(xR)故 选B x2 y2 4 （9）已知双曲线  1的一条渐近线方程为y  x，则双曲线的离心率为( A ) a2 b2 3 5 4 5 3 （A） （B） （C） （D） 3 3 4 2 b 4 c 32 42 5 解：双曲线焦点在x轴,由渐近线方程可得  ,可得e   ,故选A a 3 a 3 3 （10）若 f(sinx)3cos2x,则 f(cosx)(C ) （A）3cos2x （B）3sin2x （C）3cos2x （D）3sin2x 解： f(sinx)3cos2x3(12sin2 x)2sin2 x2 所以 f(x)2x2 2,因此 f(cosx)2cos2 x2(2cos2 x1)33cos2x故选C （11）过点（－1，0）作抛物线y  x2 x1的切线，则其中一条切线为( D ) （A）2x y20 （B）3x y30 （C）x y10 （D）x y10 第6页 | 共12页解：y2x1，设切点坐标为(x ,y )，则切线的斜率为2x 1，且y  x2 x 1 0 0 0 0 0 0 于是切线方程为yx2 x 1(2x 1)(xx )，因为点（－1，0）在切线上，可解得 0 0 0 0 x ＝0或－4，代入可验正D正确。选D 0 （12）5名志愿者分到3所学校支教，每个学校至少去一名志愿者，则不同的分派方法共有 ( A ) （A）150种 (B)180种 (C)200种 (D)280种 解：人数分配上有两种方式即1,2,2与1,1,3 C3C1C1 C1C2C2 若是1,2,2，则有 5 2 1 A3＝60种，若是1,1,3，则有 5 4 2 A3＝90种 A2 3 A2 3 2 2 所以共有150种，选A 第Ⅱ卷 二．填空题：本大题共４小题，每小题４分，共１６分，把答案填在横线上。 1 （13）在(x4  )10的展开式中常数项是45。（用数字作答） x 1 解： T Cr (x4)10r( )r Cr x405r要求常数项,即40-5r=0,可得r=8代入通项公式可 r1 10 x 10 得T C8 C2 45 r1 10 10 （14）圆O 是以R为半径的球O的小圆，若圆O 的面积S 和球O的表面积S 的比为 1 1 1 S :S 2:9，则圆心O 到球心O的距离与球半径的比OO :R1  3。 1 1 1 解：设圆O 的半径为r，则S ＝r2，S ＝4R2，由S :S 2:9得r  R＝2 2 3 1 1 1 又r2 OO2  R2，可得OO :R1  3 1 1 （15）过点(1, 2)的直线l将圆(x2)2  y2 4分成两段弧，当劣弧所对的圆心角最小时， 直线l的斜率k  ____. 解：(数形结合)由图形可知点A(1, 2)在圆(x2)2  y2 4的内部, 圆心为O(2,0)要使得 1 1 2 劣弧所对的圆心角最小,只能是直线l OA,所以k    l k  2 2 OA 第7页 | 共12页（16）一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的 频率分布直方图（如下图）。为了分析居民的收入与年龄、学历、职业等方面的关系，要从 这10000人中再用分层抽样方法抽出100人作进一步调查，则在[2500,3000)（元）月收入 段应抽出＿＿＿＿＿人。 解：由直方图可得[2500,3000)（元）月收入段共有100000.00055002500人 100 按分层抽样应抽出2500 25人 10000 频率/组距 0.0005 0.0004 0.0003 0.0002 0.0001 月收入（元） 10001500200025003000 35004000 三、解答题 2 5 5 17、解：（1）由cosC  得sinC  5 5 2 3 10 sinAsin(180 45 C) (cosCsinC) 2 10 AC 10 3 10 BC  sinA  3 2 由正弦定理知 sinB 2 10 2 AC 10 5 AB sinC   2 （2） sinB 2 5 2 1 BD AB1 2 由余弦定理知 CD BD2 BC2 2BDBCcosB 2  118213 2  13 2 （18）解：设{a }的公比为q，由S 1,S 17知q1，所以得 n 4 8 第8页 | 共12页a (q4 1) 1 1……………………………………① q1 a (q8 1) 1 17……………………………………② q1 由①、②式得 q8 1 整理得 17 q4 1 解得q4 16 所以 q＝2或q＝－2 1 将q＝2代入①式得a  ， 1 15 2n1 所以a 15 1 将q＝－2代入①式得a  ， 1 5 (1)n2n1 所以a  n 5 19解：设A 表示事件“第二箱中取出i件二等品”，i＝0，1； i B 表示事件“第三箱中取出i件二等品”，i＝0，1，2； i （1）依题意所求的概率为 C1 C2 C2 C1C1 12 P P(A B )P(A B) P(A)P(B )P(A )P(B)  4  3  4  3 2  i 1 0 0 1 1 0 0 1 C2 C2 C2 C2 25 5 5 5 5 C2 C2 12 7 (2)解法一：所求的概率为P 1P(A B )P 1 4  3   2 0 0 1 C2 C2 25 50 5 5 解法二：所求的概率为 P2P(A B)P(A B )P(A B ) 1 1 0 2 1 2 P(A)P(B )P(A )P(B )P(A)P(B ) 1 1 0 2 1 2 C1 C1C1 C2 C2 C1 C2 17  4  3 2  4  2  4  2  C2 C2 C2 C2 C2 C2 50 5 5 5 5 5 5 20．解法一： 第9页 | 共12页∥ 1 ∥ ∥ （Ⅰ）设O为AC中点，连接EO，BO，则EO CC，又CC BB，所以EO DB，EOBD ＝ 2 1 1 ＝ 1 ＝ 为平行四边形，ED∥OB． ……2分 C 1 B 1 ∵AB＝BC，∴BO⊥AC， A 1 又平面ABC⊥平面ACCA，BO面ABC，故BO⊥平面ACCA， D 1 1 1 1 ∴ED⊥平面ACCA，BD⊥AC，ED⊥CC， E 1 1 1 1 F ∴ED⊥BB，ED为异面直线AC与BB的公垂线．……6分 1 1 1 C B （Ⅱ）连接AE，由AA＝AC＝ 2AB可知，AACC为正方形， O 1 1 1 1 A ∴AE⊥AC，又由ED⊥平面ACCA和ED平面ADC知平面 1 1 1 1 1 ADC⊥平面AACC，∴AE⊥平面ADC．作EF⊥AD，垂足为F，连接AF，则AF⊥AD，∠AFE 1 1 1 1 1 1 1 1 为二面角A－AD－C的平面角． 1 1 AE× ED 2 不妨设AA＝2，则AC＝2，AB＝ 2ED＝OB＝1，EF＝ ＝ ， 1 AD 3 tan∠AFE＝ 3，∴∠AFE＝60°． 1 1 所以二面角A－AD－C为60°． ………12分 1 1 解法二： （Ⅰ）如图，建立直角坐标系O－xyz，其中原点O为AC的中点． 设A(a，0，0)，B(0，b，0)，B(0，b，2c)． 1 则C(－a，0，0)，C(－a，0，2c)，E(0，0，c)，D(0，b，c)． ……3分 1 ED＝（0，b，0），BB ＝(0，0，2c)． z 1 C 1 B 1 ED·BB ＝0，∴ED⊥BB． A 1 1 1 D E 又AC 1 ＝(－2a，0，2c)， y C B O ED·AC ＝0，∴ED⊥AC， ……6分 1 1 A x 所以ED是异面直线BB与AC的公垂线． 1 1 （Ⅱ）不妨设A(1，0，0)，则B(0，1，0)，C(－1，0，0)，A(1，0，2)， 1 BC＝(－1，－1，0)，AB＝(－1，1，0)，AA ＝(0，0，2)， 1 BC·AB＝0，BC·AA ＝0，即BC⊥AB，BC⊥AA，又AB∩AA＝A， 1 1 1 ∴BC⊥平面AAD． 1 又 E(0，0，1)，D(0，1，1)，C(－1，0，1)， EC＝(－1，0，－1)，AE＝(－1，0，1)，ED＝(0，1，0)， EC·AE＝0，EC·ED＝0，即EC⊥AE，EC⊥ED，又AE∩ED＝E， ∴ EC⊥面CAD． ……10分 1 EC·BC 1 cos＜EC，BC＞＝ ＝ ，即得EC和BC的夹角为60°． |EC|·|BC| 2 所以二面角A－AD－C为60°． ………12分 1 1 第10页 | 共12页（21）解：由f（x）为二次函数知a0 1 1 1 1 令f（x）＝0解得其两根为x   2 ,x   2 1 a a2 2 a a2 由此可知x 0,x 0 1 2 （i）当a0时，A{x|xx}{x|xx } 1 2 1 1 6 AB的充要条件是x 3，即  2 3解得a 2 a a2 7 （ii）当a0时，A{x|x xx } 1 2 1 1 AB的充要条件是x 1，即  2 1解得a2 2 a a2 6 综上，使AB成立的a的取值范围为(,2)( ,) 7 22．解：(Ⅰ)由已知条件，得F(0，1)，λ＞0． 设A(x，y)，B(x，y)．由AF＝λFB， 1 1 2 2 即得 (－x，1－y)＝λ(x，y－1)， 1 2 2 { －x ＝λx ① 1 2 1－y ＝λ(y\S\do(2)－1) ② 1 1 1 将①式两边平方并把y＝ x2，y＝ x2代入得 y＝λ2y ③ 1 4 1 2 4 2 1 2 1 解②、③式得y＝λ，y＝ ，且有xx＝－λx2＝－4λy＝－4， 1 2 λ 1 2 2 2 1 1 抛物线方程为y＝ x2，求导得y′＝ x． 4 2 所以过抛物线上A、B两点的切线方程分别是 1 1 y＝ x(x－x)＋y，y＝ x(x－x)＋y， 2 1 1 1 2 2 2 2 1 1 1 1 即y＝ xx－ x2，y＝ xx－ x2． 2 1 4 1 2 2 4 2 x ＋x x x x ＋x 1 2 1 2 1 2 解出两条切线的交点M的坐标为( ， )＝( ，－1)． ……4分 2 4 2 x 1 ＋x 2 1 1 1 所以FM·AB＝( ，－2)·(x－x，y－y)＝ (x2－x2)－2( x2－ x2)＝0 2 2 1 2 1 2 2 1 4 2 4 1 所以FM·AB为定值，其值为0． ……7分 1 (Ⅱ)由(Ⅰ)知在△ABM中，FM⊥AB，因而S＝ |AB||FM|． 2 第11页 | 共12页1 1 1 |FM|＝ (\f(x\S\do(1)＋x\S\do(2),2))＋(－2)＝ x ＋ x ＋ x x ＋4 1 2 1 2 4 4 2 1 ＝ y ＋y ＋ × (－4)＋4 1 2 2 1 1 ＝ λ＋ ＋2＝ λ＋ ． λ λ 因为|AF|、|BF|分别等于A、B到抛物线准线y＝－1的距离，所以 1 1 |AB|＝|AF|＋|BF|＝y＋y＋2＝λ＋ ＋2＝( λ＋ )2． 1 2 λ λ 1 1 于是 S＝ |AB||FM|＝( λ＋ )3， 2 λ 1 由 λ＋ ≥2知S≥4，且当λ＝1时，S取得最小值4． λ 第12页 | 共12页