文档内容
第1 页共4 页
湖北省2024-2025 学年秋季学期高二期末联考
数学参考答案及评分标准
(2025.1)
一、单选题:1-8:CBBA DACD
二、多选题:9.BD
10.ABD
11.ACD
三、填空题:12.
5
2
13. 3
4
14.
1012
2
7
7
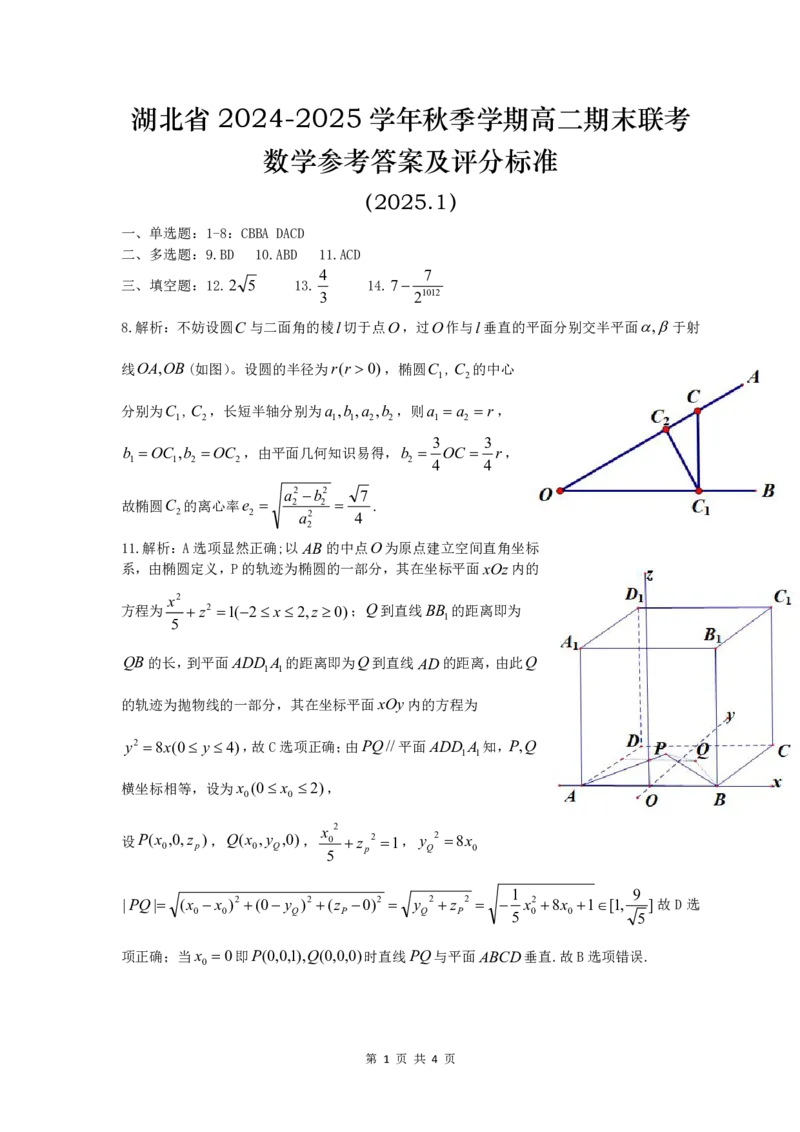
8.解析:不妨设圆C 与二面角的棱l 切于点O ,过O 作与l 垂直的平面分别交半平面
,
于射
线
OB
OA,
(如图)。设圆的半径为
)
0
(
r
r
,椭圆
1
C ,
2
C 的中心
分别为
1
C ,
2
C ,长短半轴分别为
2
2
1
1
,
,
,
b
a
b
a
,则
r
a
a
2
1
,
2
2
1
1
,
OC
b
OC
b
,由平面几何知识易得,
r
OC
b
4
3
4
3
2
,
故椭圆
2
C 的离心率
4
7
2
2
2
2
2
2
2
a
b
a
e
.
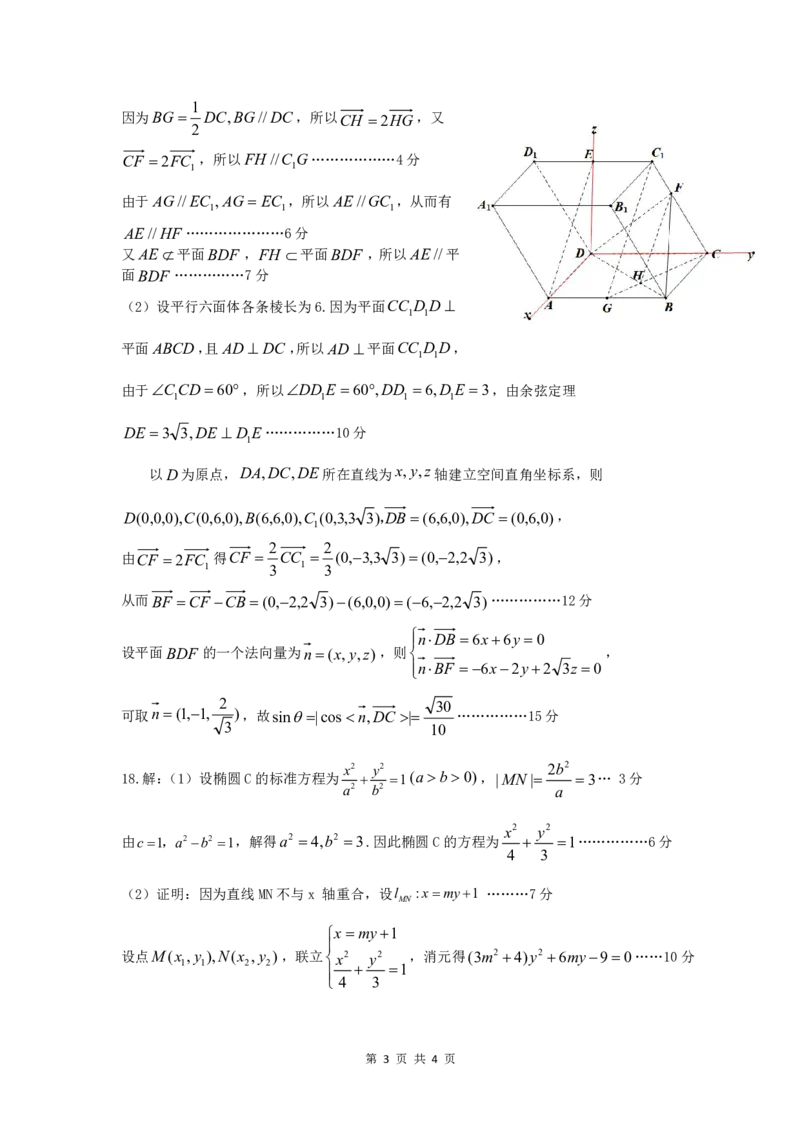
11.解析:A 选项显然正确;以AB 的中点O 为原点建立空间直角坐标
系,由椭圆定义,P 的轨迹为椭圆的一部分,其在坐标平面xOz 内的
方程为
)
0
,2
2
(1
5
2
2
z
x
z
x
;Q 到直线
1
BB 的距离即为
QB 的长,到平面
1
1A
ADD
的距离即为Q 到直线AD 的距离,由此Q
的轨迹为抛物线的一部分,其在坐标平面xOy 内的方程为
)
4
0
(
8
2
y
x
y
,故C 选项正确;由
//
PQ
平面
1
1A
ADD
知,
Q
P,
横坐标相等,设为
)
2
0
(
0
0
x
x
,
设
)
,0,
(
0
pz
x
P
,
)
0,
,
(
0
Q
y
x
Q
,
1
5
2
2
0
pz
x
,
0
2
8x
yQ
]
5
9
,1[
1
8
5
1
)
0
(
)
0
(
)
(
|
|
0
2
0
2
2
2
2
2
0
0
x
x
z
y
z
y
x
x
PQ
P
Q
P
Q
故D 选
项正确;当
0
0
x
即
)
0,0,0
(
),
1,0,0
(
Q
P
时直线PQ 与平面ABCD 垂直.故B 选项错误.
第2 页共4 页
14.解析:由
1
2
a ,1
2
2
1
1
,
2
4
a a
a
得
,
1
1
2
1
1
1
,
2
2
n
n
n
n
n
n
a
a
a
a
得
2
1
2
n
n
a
a
所以
,
,
,
5
3
1
a
a
a
以及
,
,
,
6
4
2
a
a
a
分别是公比为1
2 的等比数列,
当n 为奇数时,
1
2
1
2 2
n
na
,当n 为偶数时,
2
2
2
2
1 1
1
4 2
2
n
n
na
所以,当n 为奇数时,
1
3
1
2
2
2
1
1
1
9 1
2 2
2
4 2
n
n
n
n
n
n
b
a
a
,
当n 为偶数时,
2
2
2
2
1
1
1
5 1
2
2
2
2 2
n
n
n
n
n
n
b
a
a
,
2024
1
3
2023
2
4
2024
T
b
b
b
b
b
b
1012
1012
1012
9
1
5
1
7
1
1
7
2
2
2
2
2
.
三、解答题:
15.解:(1)由已知,
n
n
n
n
n
b
a
a
a
b
2
)1
(
2
2
2
1
1
1
,且
2
1
1
1
a
b
所以数列
}
{ nb
是以2 为首项,2 为公比的等比数列…5 分
(2)由(1)知,
1
2
,
2
n
n
n
n
a
b
,所以
1
2
n
c
n
n
…………8 分
)]
1
(
2
1
0
[
)
2
2
2
(
2
1
2
1
n
c
c
c
S
n
n
n
2
2
1
2
1
2
2
)1
(
2
1
)
2
1(
2
2
1
n
n
n
n
n
n
………………13 分
16.解:(1)由圆的性质知,弦AB 被点
0P 平分即为
AB
C
P
0
,,故
1
AB
k
…………3 分
所以直线
1
2
:
x
y
AB
,即
0
1
y
x
…………6 分
(2)(ⅰ)当AB 的斜率不存在时,直线为
1
x
,此时
3
2
|
|
AB
,符合题意……8 分
(ⅱ)当直线AB 的斜率存在时,设
)1
(
2
:
x
k
y
AB
,变形为
0
2
k
y
kx
……9 分
圆心到直线AB 的距离
1
|1
|
2
k
k
d
…………11 分
由勾股定理得,
1
,4
)
3
(
2
2
d
d
,解得
0
k
,直线
2
:
y
AB
综上,直线AB 的方程为
1
x
或
2
y
.…………15 分
17.(1)证明如图,取AB 的中点G ,连接CG 交BD 于H ,连接
G
C
FH
1
,
……………2 分
第3 页共4 页
因为
DC
BG
DC
BG
//
,
2
1
,所以
HG
CH
2
,又
1
2FC
CF
,所以
G
C
FH
1
//
………………4 分
由于
1
1,
//
EC
AG
EC
AG
,所以
1
// GC
AE
,从而有
HF
AE //
…………………6 分
又
AE
平面BDF ,
FH
平面BDF ,所以
//
AE
平
面BDF ……………7 分
(2)设平行六面体各条棱长为6.因为平面
D
D
CC
1
1
平面ABCD ,且
DC
AD
,所以
AD
平面
D
D
CC
1
1
,
由于
60
1CD
C
,所以
3
,6
,
60
1
1
1
E
D
DD
E
DD
,由余弦定理
E
D
DE
DE
1
,3
3
……………10 分
以D 为原点,
DE
DC
DA
,
,
所在直线为
z
y
x
,
,
轴建立空间直角坐标系,则
)
0,6,0
(
),
0,6,6
(
)
3
3,3,0
(
),
0,6,6
(
),
0,6,0
(
),
0,0,0
(
1
DC
DB
C
B
C
D
,
,
由
1
2FC
CF
得
)
3
2,2
,0
(
)
3
3,3
,0
(
3
2
3
2
1
CC
CF
,
从而
)
3
2,2
,6
(
)
0,0,6
(
)
3
2,2
,0
(
CB
CF
BF
……………12 分
设平面BDF 的一个法向量为
)
,
,
(
z
y
x
n
,则
0
3
2
2
6
0
6
6
z
y
x
BF
n
y
x
DB
n
,
可取
)
3
2
,1
,1(
n
,故
10
30
|
,
cos
|
sin
DC
n
……………15 分
18.解:(1)设椭圆C 的标准方程为
2
2
2
2
1
x
y
a
b
)
0
(
b
a
,
3
2
|
|
2
a
b
MN
… 3 分
由
2
2
1
1
c
a
b
,
,解得
3
,4
2
2
b
a
.因此椭圆C 的方程为
1
3
4
2
2
y
x
……………6 分
(2)证明:因为直线MN 不与x 轴重合,设
:
1
MN
l
x
my
………7 分
设点
)
,
(
),
,
(
2
2
1
1
y
x
N
y
x
M
,联立
1
3
4
1
2
2
y
x
my
x
,消元得
0
9
6
)
4
3
(
2
2
my
y
m
……10 分
第4 页共4 页
得
)
(
4
3
9
4
3
6
2
2
1
2
2
1
m
y
y
m
m
y
y
,且
0
恒成立……………12 分
所以
9
)
(
3
)
3
)(
3
(
2
1
2
1
2
2
1
2
1
2
1
y
y
m
y
y
m
y
y
my
my
y
y
k
k
AN
AM
……14 分
将
)
(代入化简得
4
1
AN
AM k
k
所以直线
NA
MA,
的斜率之积为
4
1
……………17 分
19.解:设第i 次操作后A,B 两个盒子里球的个数分别为
)
,
,2,1
(
,
n
i
b
a
i
i
(1)列举
)
,
(
1
1 b
a
所有8 种可能的情形:
)
13
,7
(
),
12
,7
(
),
13
,8
(
),
12
,8
(
)
10
,
11
(
),
9,
11
(
),
10
,
10
(
),
9
10
(
,
,
……………3 分
满足
1
1
b
a
的有3 种情形,所以
8
3
)
(
A
P
……………5 分
(2)设
b
b
a
a
0
0
,
,在第
)
,
,2,1
(
n
i
i
次操作结果有8 种等可能的情形,
①当
1
,1
1
1
i
i
i
i
b
b
a
a
或
2
,2
1
1
i
i
i
i
b
b
a
a
,或
1
,1
1
1
i
i
i
i
b
b
a
a
或
2
,2
1
1
i
i
i
i
b
b
a
a
时,
1
1
i
i
i
i
b
a
b
a
…………………7 分
②当
1
,2
1
1
i
i
i
i
b
b
a
a
或
2
,1
1
1
i
i
i
i
b
b
a
a
时,
1
1
1
i
i
i
i
b
a
b
a
……8 分
③当
1
,2
1
1
1
i
i
i
i
b
b
a
a
或
2
,1
1
1
1
i
i
i
i
b
b
a
a
时,
1
1
1
i
i
i
i
b
a
b
a
……9 分
仅有③中所述2 种情形是减少的,
故一次操作后A,B 两个盒子里球的个数之和减少的概率为
4
1
8
2
p
……………11 分
(3)由(2)的讨论知,每一次操作,A,B 两个盒子里球的个数之和有3 种可能的变化:增加1
个、不变、减少1 个,要满足本n 次操作后,A,B 两个盒子里球的个数之和为
n
b
a
,即比
初始值
b
a
增加n 个,则只可能是每一次操作均增加1 个小球。
由(2)知,每次操作小球增加1 个的概率为
4
1
8
2
p
……………14 分
由于每一次操作结果均独立,本n 次操作均增加1 个的概率为
n
n
)
4
1
(
4
1
4
1
4
1
个
故A,B 两个盒子里球的个数之和为
n
b
a
的概率为
n)
4
1
(
……………17 分