文档内容
http://t.cn/Ri466E4
苏教版数学六年级下学期期末测试卷
一、认真读题,谨慎填写.(共25分)
1.1.25立方厘米= 毫升
300立方分米= 立方米
1.8升= 立方分米.
2.
桃树和梨树的棵数比是 ,梨树占桃树的 ,桃树占总棵数的 ,梨树比桃
树多 .
3.一个圆柱体,底面半径是2厘米,高3厘米.这个圆柱体的底面积是 平方
厘米;它的侧面积 平方厘米;它的表面积是 平方厘米;它的体
积是 立方厘米.与它等底等高圆锥的体积是 立方厘米.
4.用一张长15厘米,宽12厘米的长方形纸围成一个圆柱,这个圆柱的侧面积是
平方厘米.
5.一种压路机的前轮是圆柱形,轮宽2米,直径1米.前轮滚动一周,压路机前进
米,压路的面积是 平方米.
6.一个圆柱的底面半径扩大3倍,高不变,它的侧面积扩大 倍,体积扩大
倍.
7.把圆柱的侧面沿着高的方向展开,得到一个边长是6.28分米的正方形,这个圆柱的高
是 分米,底面积是 平方分米.
8.一个圆锥的体积是18立方分米,高是6分米,底面积是 .
9.一个圆锥的体积比与它等底等高的圆柱体积少48立方分米,圆锥的体积是
立方分米,圆柱的体积是 立方分米.
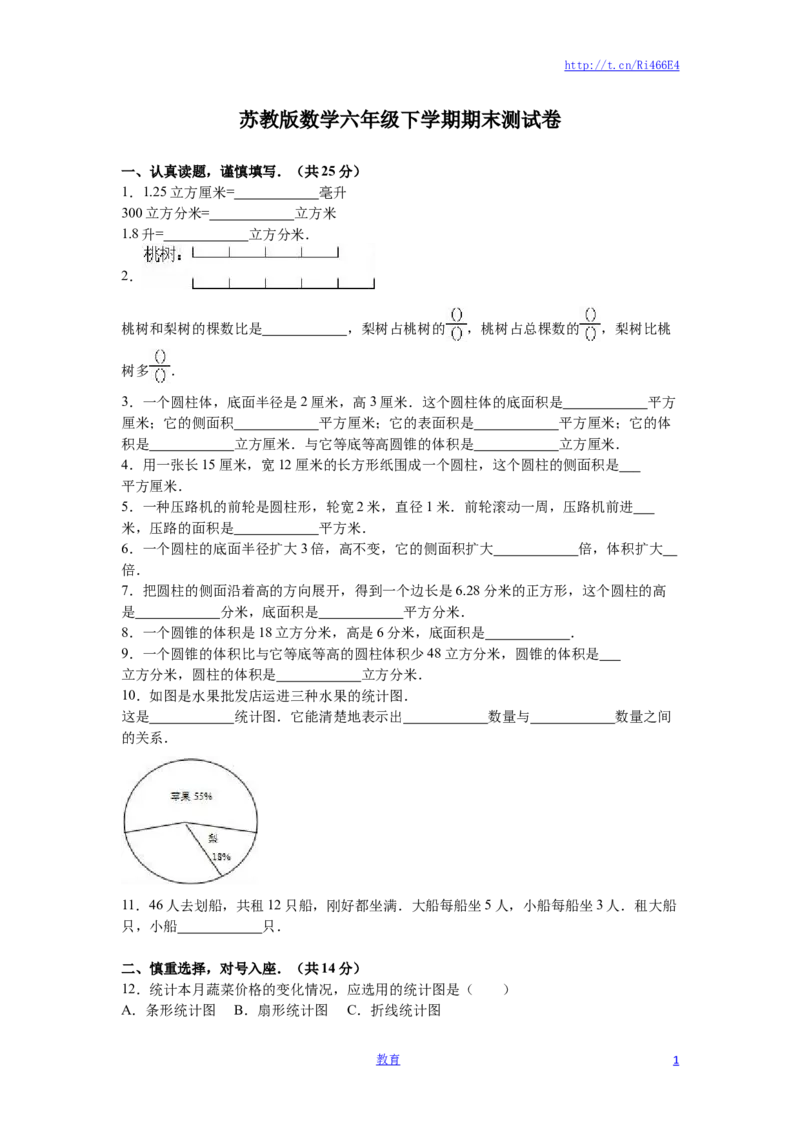
10.如图是水果批发店运进三种水果的统计图.
这是 统计图.它能清楚地表示出 数量与 数量之间
的关系.
11.46人去划船,共租12只船,刚好都坐满.大船每船坐5人,小船每船坐3人.租大船
只,小船 只.
二、慎重选择,对号入座.(共14分)
12.统计本月蔬菜价格的变化情况,应选用的统计图是( )
A.条形统计图 B.扇形统计图 C.折线统计图
教育 1http://t.cn/Ri466E4
13.做一个圆柱形通风管,需要多少铁皮?是求圆柱的( )
A.体积B.容积 C.表面积 D.侧面积
14.把底面直径和高相等的圆柱的侧面展开可能是( )
A.梯形B.长方形
C.正方形 D.以上答案都不对
15.把一个圆柱削成一个最大的圆锥,削去部分的体积是这个圆柱体积的( )
A. B. C.2倍
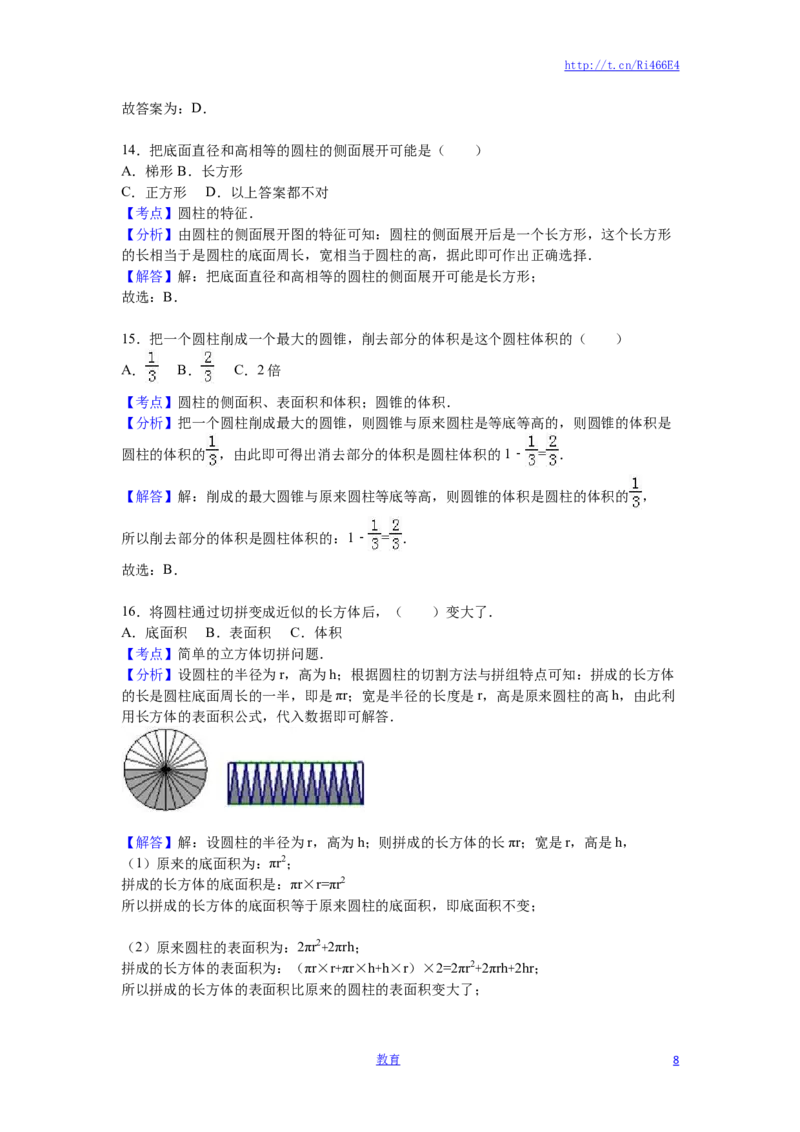
16.将圆柱通过切拼变成近似的长方体后,( )变大了.
A.底面积 B.表面积 C.体积
17.用一块长25.12厘米,宽18.84厘米的长方形铁皮,配上、下面( )圆形铁片,正
好可以做成圆柱形容器.
A.r=8cm B.d=4cm C.r=3cm D.d=3cm
18.一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米.
A.50.24B.100.48 C.64
三、一丝不苟,细心计算.
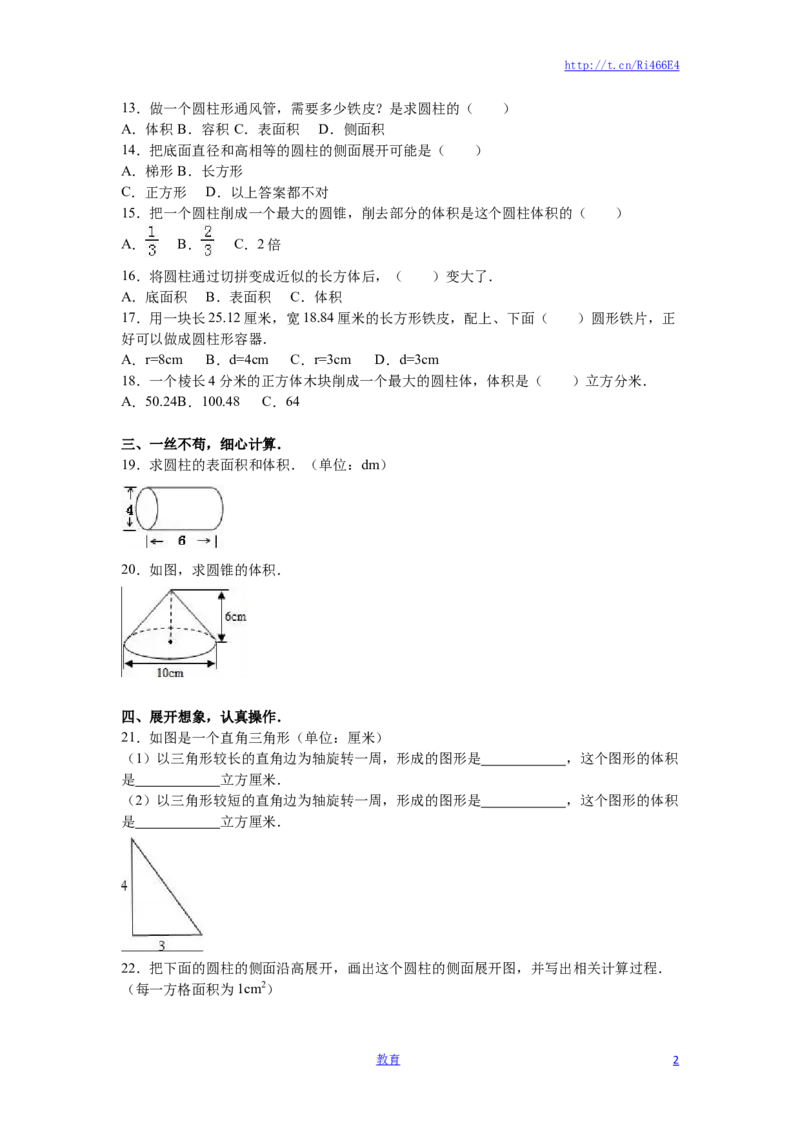
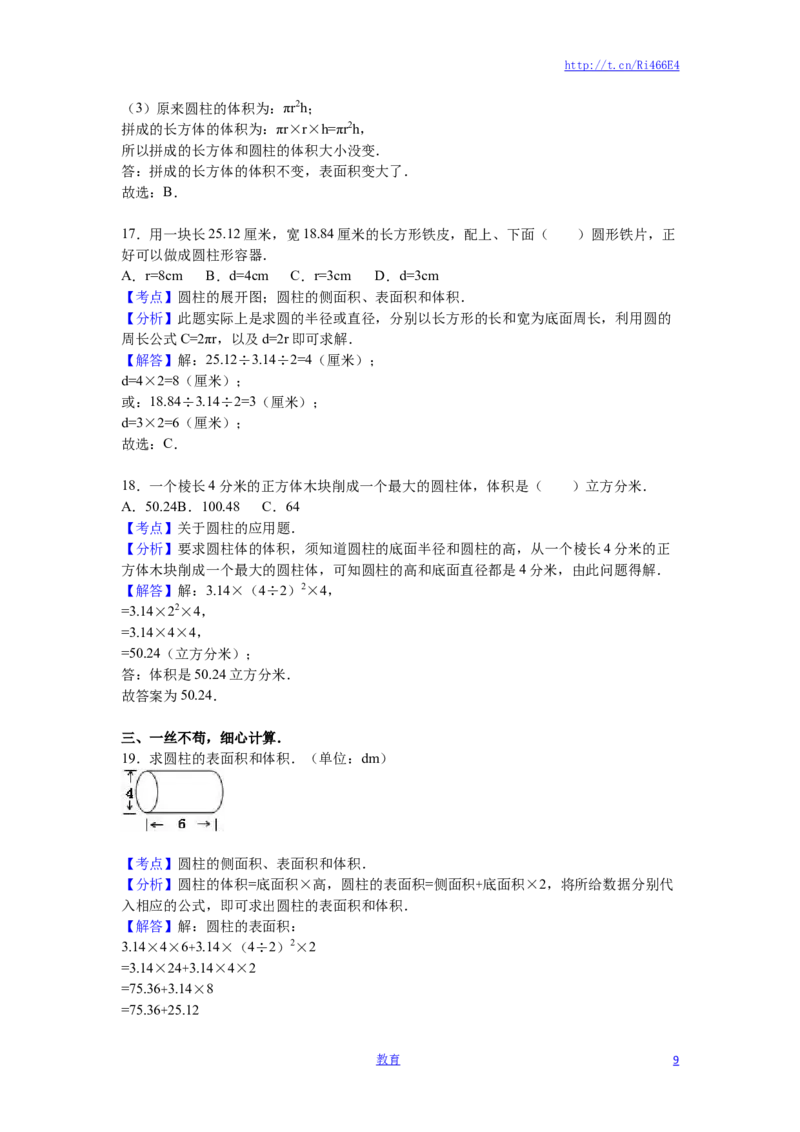
19.求圆柱的表面积和体积.(单位:dm)
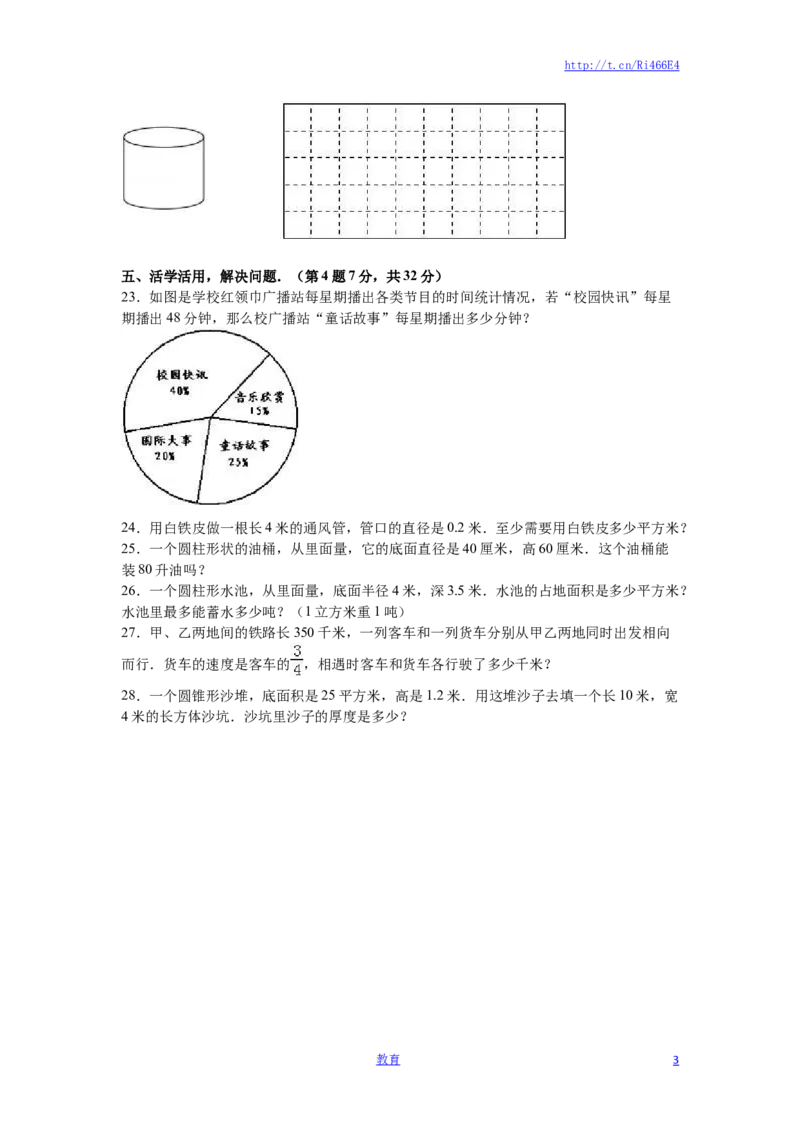
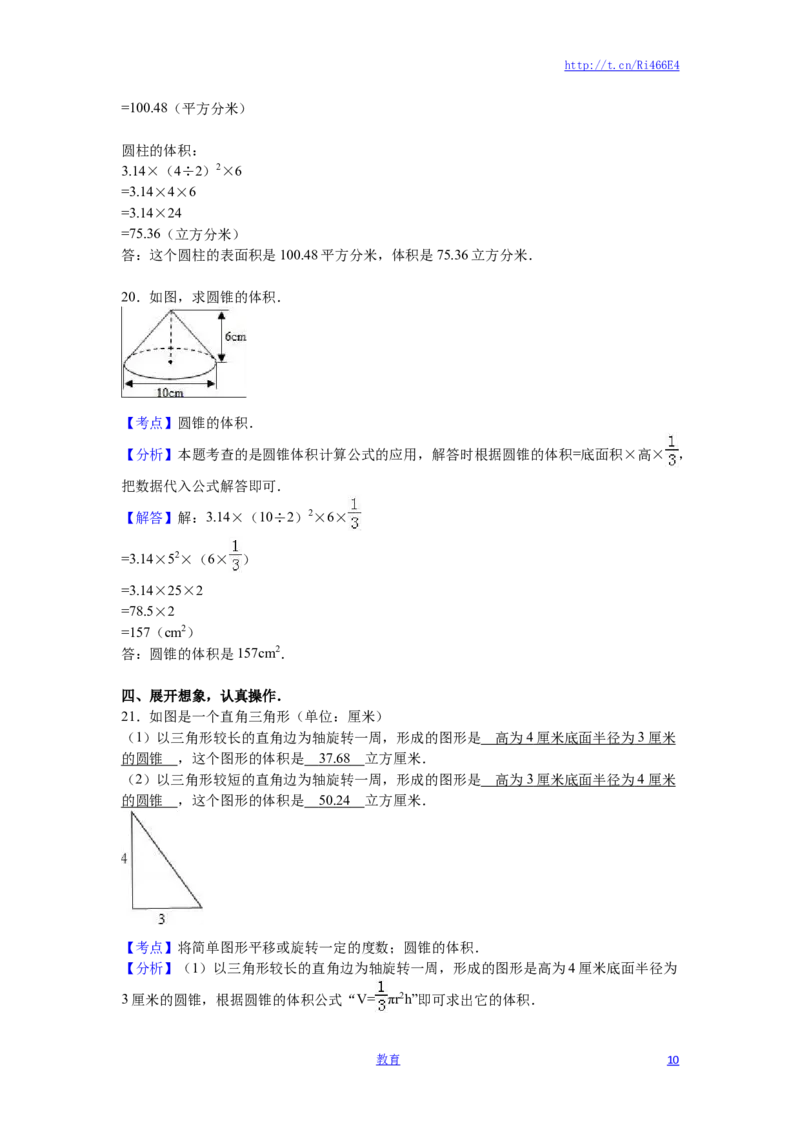
20.如图,求圆锥的体积.
四、展开想象,认真操作.
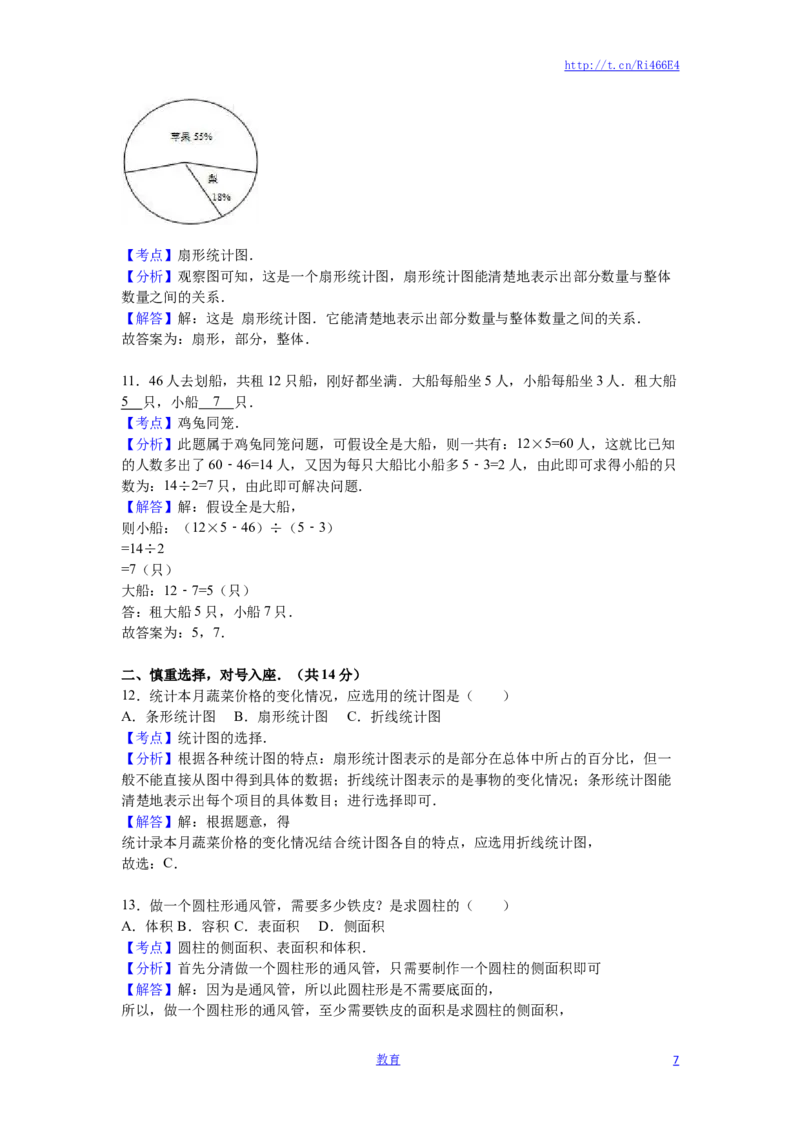
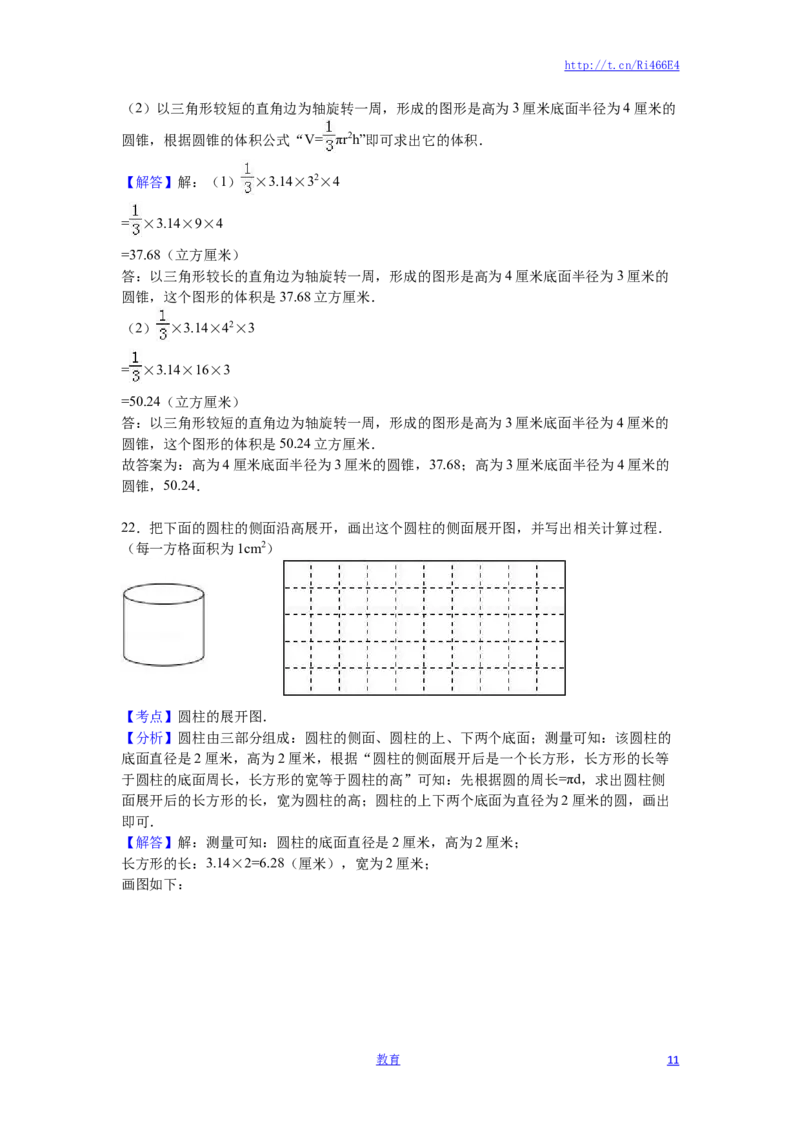
21.如图是一个直角三角形(单位:厘米)
(1)以三角形较长的直角边为轴旋转一周,形成的图形是 ,这个图形的体积
是 立方厘米.
(2)以三角形较短的直角边为轴旋转一周,形成的图形是 ,这个图形的体积
是 立方厘米.
22.把下面的圆柱的侧面沿高展开,画出这个圆柱的侧面展开图,并写出相关计算过程.
(每一方格面积为1cm2)
教育 2http://t.cn/Ri466E4
五、活学活用,解决问题.(第4题7分,共32分)
23.如图是学校红领巾广播站每星期播出各类节目的时间统计情况,若“校园快讯”每星
期播出48分钟,那么校广播站“童话故事”每星期播出多少分钟?
24.用白铁皮做一根长4米的通风管,管口的直径是0.2米.至少需要用白铁皮多少平方米?
25.一个圆柱形状的油桶,从里面量,它的底面直径是40厘米,高60厘米.这个油桶能
装80升油吗?
26.一个圆柱形水池,从里面量,底面半径4米,深3.5米.水池的占地面积是多少平方米?
水池里最多能蓄水多少吨?(1立方米重1吨)
27.甲、乙两地间的铁路长350千米,一列客车和一列货车分别从甲乙两地同时出发相向
而行.货车的速度是客车的 ,相遇时客车和货车各行驶了多少千米?
28.一个圆锥形沙堆,底面积是25平方米,高是1.2米.用这堆沙子去填一个长10米,宽
4米的长方体沙坑.沙坑里沙子的厚度是多少?
教育 3http://t.cn/Ri466E4
参考答案与试题解析
一、认真读题,谨慎填写.(共25分)
1.1.25立方厘米= 1.2 5 毫升
300立方分米= 0. 3 立方米
1.8升= 1. 8 立方分米.
【考点】体积、容积进率及单位换算.
【分析】(1)立方厘米与毫升是等量关系二者互化数值不变.
(2)低级单位立方分米化高级单位立方米除以进率1000.
(3)立方分米与升是等量关系二者互化数值不变.
【解答】解:(1)1.25立方厘米=1.25毫升;
(2)300立方分米=0.3立方米;
(3)0.8升=1.8立方分米.
故答案为:1.25,0.3,1.8.
2.
桃树和梨树的棵数比是 4 : 5 ,梨树占桃树的 ,桃树占总棵数的 ,梨树比桃树多
.
【考点】分数除法应用题;比的意义.
【分析】由图可知,桃树与梨树总棵数被平均分成9份,其中桃树4份,梨树5份,根据
比的意义,桃树与梨树棵数的比是4:5,将桃树棵数当作单位“1”,根据分数的意义,梨
树占桃树的5÷4= ,将总棵数当作单位“1”,则桃树占总棵数的4÷9= ,又梨树比桃树
多5﹣4份,则梨树比桃树多(5﹣1)÷4= .
【解答】解:桃树与梨树棵数的比是4:5,
5÷4= ,
4÷9= ,
(5﹣1)÷4
=1÷4
= .
即桃树和梨树的棵数比是4:5,梨树占桃树的 ,桃树占总棵数的 ,梨树比桃树多 .
故答案为:4:5, , , .
教育 4http://t.cn/Ri466E4
3.一个圆柱体,底面半径是2厘米,高3厘米.这个圆柱体的底面积是 12.5 6 平方厘米;
它的侧面积 37.6 8 平方厘米;它的表面积是 62. 8 平方厘米;它的体积是 37.6 8 立
方厘米.与它等底等高圆锥的体积是 12.5 6 立方厘米.
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【分析】根据圆的面积公式:s=πr2,圆柱的侧面积公式:s=ch,圆柱的表面积公式:圆柱
的表面积=侧面积+底面积×2,圆柱的体积公式:v=sh,圆锥的体积公式:v ,把数据
分别代入公式解答即可.
【解答】解:3.14×22
=3.14×4
=12.56(平方厘米),
2×3.14×2×3
=12.56×3
=37.68(平方厘米),
37.68+12.56×2
=37.68+25.12
=62.8(平方厘米),
12.56×3=37.68(立方厘米),
37.68× =12.56(立方厘米),
答:这个圆柱体的底面积是12.56平方厘米;它的侧面积37.68平方厘米;它的表面积是
628平方厘米;它的体积是37.68立方厘米.与它等底等高圆锥的体积是12.56立方厘米.
故答案为:12.56;37.68;62.8;37.68;12.56.
4.用一张长15厘米,宽12厘米的长方形纸围成一个圆柱,这个圆柱的侧面积是 18 0
平方厘米.
【考点】圆柱的侧面积、表面积和体积.
【分析】根据圆柱的侧面展开图的特点:圆柱的底面周长是长方形的长,圆柱的高是长方
形的宽可知,这个圆柱的侧面积就是这个长方形纸的面积.
【解答】解:15×12=180(平方厘米),
答:这个圆柱的侧面积是180平方厘米.
故答案为:180.
5.一种压路机的前轮是圆柱形,轮宽2米,直径1米.前轮滚动一周,压路机前进 3.1 4
米,压路的面积是 6.2 8 平方米.
【考点】关于圆柱的应用题.
【分析】根据圆的周长公式:c=πd,把数据代入公式即可求出压路机前进多少米,再根据
长方形的面积公式:s=ab,用压路机前进的米数乘轮宽即可.
【解答】解:3.14×1=3.14(米),
3.14×2=6.28(平方米),
答:压路机前进3.14米,压路的面积是6.28平方米.
故答案为:3.14;6.28.
6.一个圆柱的底面半径扩大3倍,高不变,它的侧面积扩大 3 倍,体积扩大 9 倍.
教育 5http://t.cn/Ri466E4
【考点】圆柱的侧面积、表面积和体积;积的变化规律.
【分析】根据圆柱侧面积=2π×圆柱底面半径×高,圆柱体积=π×(圆柱底面半径)2×高
解答即可.
【解答】解:圆柱底面半径扩大3倍,高不变,侧面积就扩大3倍,体积扩大3×3=9倍.
故答案为:3;9.
7.把圆柱的侧面沿着高的方向展开,得到一个边长是6.28分米的正方形,这个圆柱的高
是 6.2 8 分米,底面积是 3.1 4 平方分米.
【考点】圆柱的展开图;圆、圆环的周长;圆、圆环的面积.
【分析】根据圆柱体的特征可知,侧面展开是一个长方形(正方形是特殊的长方形),这
个长方形的长等于圆柱体的底面周长,宽等于圆柱体的高;已知一个圆柱的侧面沿着高展
开后是一个边长6.28分米的正方形,也就是圆柱体的底面周长和高都是6.28分米,再利用
圆的面积公式解答即可.
【解答】解:6.28÷3.14÷2=1(分米);
3.14×12=3.14(平方分米);
答:这个圆柱体的高是6.28分米,底面积是3.14平方分米.
故答案为:6.28、3.14.
8.一个圆锥的体积是18立方分米,高是6分米,底面积是 9 平方分米 .
【考点】圆锥的体积.
【分析】由“圆锥体的体积= ×底面积×高”可得“底面积=圆锥体的体积×3÷高”,圆
锥体的体积和高已知,代入公式即可求解.
【解答】解:18×3÷6,
=54÷6,
=9(平方分米);
答:这个圆锥体的底面积是9平方分米.
故填:9平方分米.
9.一个圆锥的体积比与它等底等高的圆柱体积少48立方分米,圆锥的体积是 2 4 立方
分米,圆柱的体积是 7 2 立方分米.
【考点】圆锥的体积.
【分析】因为等底等高的圆柱的体积是圆锥体积的倍,所以等底等高的圆柱与圆锥的体积
差相当于圆锥体积的(3﹣1)倍,由此可以求出圆锥的体积,进而求出圆柱的体积.
【解答】解:48÷(3﹣1)
=48÷2
=24(立方分米),
24×3=72(立方分米),
答:圆锥的体积是24立方分米,圆柱的体积是72立方分米.
故答案为:24;72.
10.如图是水果批发店运进三种水果的统计图.
这是 扇形 统计图.它能清楚地表示出 部分 数量与 整体 数量之间的关系.
教育 6http://t.cn/Ri466E4
【考点】扇形统计图.
【分析】观察图可知,这是一个扇形统计图,扇形统计图能清楚地表示出部分数量与整体
数量之间的关系.
【解答】解:这是 扇形统计图.它能清楚地表示出部分数量与整体数量之间的关系.
故答案为:扇形,部分,整体.
11.46人去划船,共租12只船,刚好都坐满.大船每船坐5人,小船每船坐3人.租大船
5 只,小船 7 只.
【考点】鸡兔同笼.
【分析】此题属于鸡兔同笼问题,可假设全是大船,则一共有:12×5=60人,这就比已知
的人数多出了60﹣46=14人,又因为每只大船比小船多5﹣3=2人,由此即可求得小船的只
数为:14÷2=7只,由此即可解决问题.
【解答】解:假设全是大船,
则小船:(12×5﹣46)÷(5﹣3)
=14÷2
=7(只)
大船:12﹣7=5(只)
答:租大船5只,小船7只.
故答案为:5,7.
二、慎重选择,对号入座.(共14分)
12.统计本月蔬菜价格的变化情况,应选用的统计图是( )
A.条形统计图 B.扇形统计图 C.折线统计图
【考点】统计图的选择.
【分析】根据各种统计图的特点:扇形统计图表示的是部分在总体中所占的百分比,但一
般不能直接从图中得到具体的数据;折线统计图表示的是事物的变化情况;条形统计图能
清楚地表示出每个项目的具体数目;进行选择即可.
【解答】解:根据题意,得
统计录本月蔬菜价格的变化情况结合统计图各自的特点,应选用折线统计图,
故选:C.
13.做一个圆柱形通风管,需要多少铁皮?是求圆柱的( )
A.体积B.容积 C.表面积 D.侧面积
【考点】圆柱的侧面积、表面积和体积.
【分析】首先分清做一个圆柱形的通风管,只需要制作一个圆柱的侧面积即可
【解答】解:因为是通风管,所以此圆柱形是不需要底面的,
所以,做一个圆柱形的通风管,至少需要铁皮的面积是求圆柱的侧面积,
教育 7http://t.cn/Ri466E4
故答案为:D.
14.把底面直径和高相等的圆柱的侧面展开可能是( )
A.梯形B.长方形
C.正方形 D.以上答案都不对
【考点】圆柱的特征.
【分析】由圆柱的侧面展开图的特征可知:圆柱的侧面展开后是一个长方形,这个长方形
的长相当于是圆柱的底面周长,宽相当于圆柱的高,据此即可作出正确选择.
【解答】解:把底面直径和高相等的圆柱的侧面展开可能是长方形;
故选:B.
15.把一个圆柱削成一个最大的圆锥,削去部分的体积是这个圆柱体积的( )
A. B. C.2倍
【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【分析】把一个圆柱削成最大的圆锥,则圆锥与原来圆柱是等底等高的,则圆锥的体积是
圆柱的体积的 ,由此即可得出消去部分的体积是圆柱体积的1﹣ = .
【解答】解:削成的最大圆锥与原来圆柱等底等高,则圆锥的体积是圆柱的体积的 ,
所以削去部分的体积是圆柱体积的:1﹣ = .
故选:B.
16.将圆柱通过切拼变成近似的长方体后,( )变大了.
A.底面积 B.表面积 C.体积
【考点】简单的立方体切拼问题.
【分析】设圆柱的半径为r,高为h;根据圆柱的切割方法与拼组特点可知:拼成的长方体
的长是圆柱底面周长的一半,即是πr;宽是半径的长度是r,高是原来圆柱的高h,由此利
用长方体的表面积公式,代入数据即可解答.
【解答】解:设圆柱的半径为r,高为h;则拼成的长方体的长πr;宽是r,高是h,
(1)原来的底面积为:πr2;
拼成的长方体的底面积是:πr×r=πr2
所以拼成的长方体的底面积等于原来圆柱的底面积,即底面积不变;
(2)原来圆柱的表面积为:2πr2+2πrh;
拼成的长方体的表面积为:(πr×r+πr×h+h×r)×2=2πr2+2πrh+2hr;
所以拼成的长方体的表面积比原来的圆柱的表面积变大了;
教育 8http://t.cn/Ri466E4
(3)原来圆柱的体积为:πr2h;
拼成的长方体的体积为:πr×r×h=πr2h,
所以拼成的长方体和圆柱的体积大小没变.
答:拼成的长方体的体积不变,表面积变大了.
故选:B.
17.用一块长25.12厘米,宽18.84厘米的长方形铁皮,配上、下面( )圆形铁片,正
好可以做成圆柱形容器.
A.r=8cm B.d=4cm C.r=3cm D.d=3cm
【考点】圆柱的展开图;圆柱的侧面积、表面积和体积.
【分析】此题实际上是求圆的半径或直径,分别以长方形的长和宽为底面周长,利用圆的
周长公式C=2πr,以及d=2r即可求解.
【解答】解:25.12÷3.14÷2=4(厘米);
d=4×2=8(厘米);
或:18.84÷3.14÷2=3(厘米);
d=3×2=6(厘米);
故选:C.
18.一个棱长4分米的正方体木块削成一个最大的圆柱体,体积是( )立方分米.
A.50.24B.100.48 C.64
【考点】关于圆柱的应用题.
【分析】要求圆柱体的体积,须知道圆柱的底面半径和圆柱的高,从一个棱长4分米的正
方体木块削成一个最大的圆柱体,可知圆柱的高和底面直径都是4分米,由此问题得解.
【解答】解:3.14×(4÷2)2×4,
=3.14×22×4,
=3.14×4×4,
=50.24(立方分米);
答:体积是50.24立方分米.
故答案为50.24.
三、一丝不苟,细心计算.
19.求圆柱的表面积和体积.(单位:dm)
【考点】圆柱的侧面积、表面积和体积.
【分析】圆柱的体积=底面积×高,圆柱的表面积=侧面积+底面积×2,将所给数据分别代
入相应的公式,即可求出圆柱的表面积和体积.
【解答】解:圆柱的表面积:
3.14×4×6+3.14×(4÷2)2×2
=3.14×24+3.14×4×2
=75.36+3.14×8
=75.36+25.12
教育 9http://t.cn/Ri466E4
=100.48(平方分米)
圆柱的体积:
3.14×(4÷2)2×6
=3.14×4×6
=3.14×24
=75.36(立方分米)
答:这个圆柱的表面积是100.48平方分米,体积是75.36立方分米.
20.如图,求圆锥的体积.
【考点】圆锥的体积.
【分析】本题考查的是圆锥体积计算公式的应用,解答时根据圆锥的体积=底面积×高× ,
把数据代入公式解答即可.
【解答】解:3.14×(10÷2)2×6×
=3.14×52×(6× )
=3.14×25×2
=78.5×2
=157(cm2)
答:圆锥的体积是157cm2.
四、展开想象,认真操作.
21.如图是一个直角三角形(单位:厘米)
(1)以三角形较长的直角边为轴旋转一周,形成的图形是 高为 4 厘米底面半径为 3 厘米
的圆锥 ,这个图形的体积是 37.6 8 立方厘米.
(2)以三角形较短的直角边为轴旋转一周,形成的图形是 高为 3 厘米底面半径为 4 厘米
的圆锥 ,这个图形的体积是 50.2 4 立方厘米.
【考点】将简单图形平移或旋转一定的度数;圆锥的体积.
【分析】(1)以三角形较长的直角边为轴旋转一周,形成的图形是高为4厘米底面半径为
3厘米的圆锥,根据圆锥的体积公式“V= πr2h”即可求出它的体积.
教育 10http://t.cn/Ri466E4
(2)以三角形较短的直角边为轴旋转一周,形成的图形是高为3厘米底面半径为4厘米的
圆锥,根据圆锥的体积公式“V= πr2h”即可求出它的体积.
【解答】解:(1) ×3.14×32×4
= ×3.14×9×4
=37.68(立方厘米)
答:以三角形较长的直角边为轴旋转一周,形成的图形是高为4厘米底面半径为3厘米的
圆锥,这个图形的体积是37.68立方厘米.
(2) ×3.14×42×3
= ×3.14×16×3
=50.24(立方厘米)
答:以三角形较短的直角边为轴旋转一周,形成的图形是高为3厘米底面半径为4厘米的
圆锥,这个图形的体积是50.24立方厘米.
故答案为:高为4厘米底面半径为3厘米的圆锥,37.68;高为3厘米底面半径为4厘米的
圆锥,50.24.
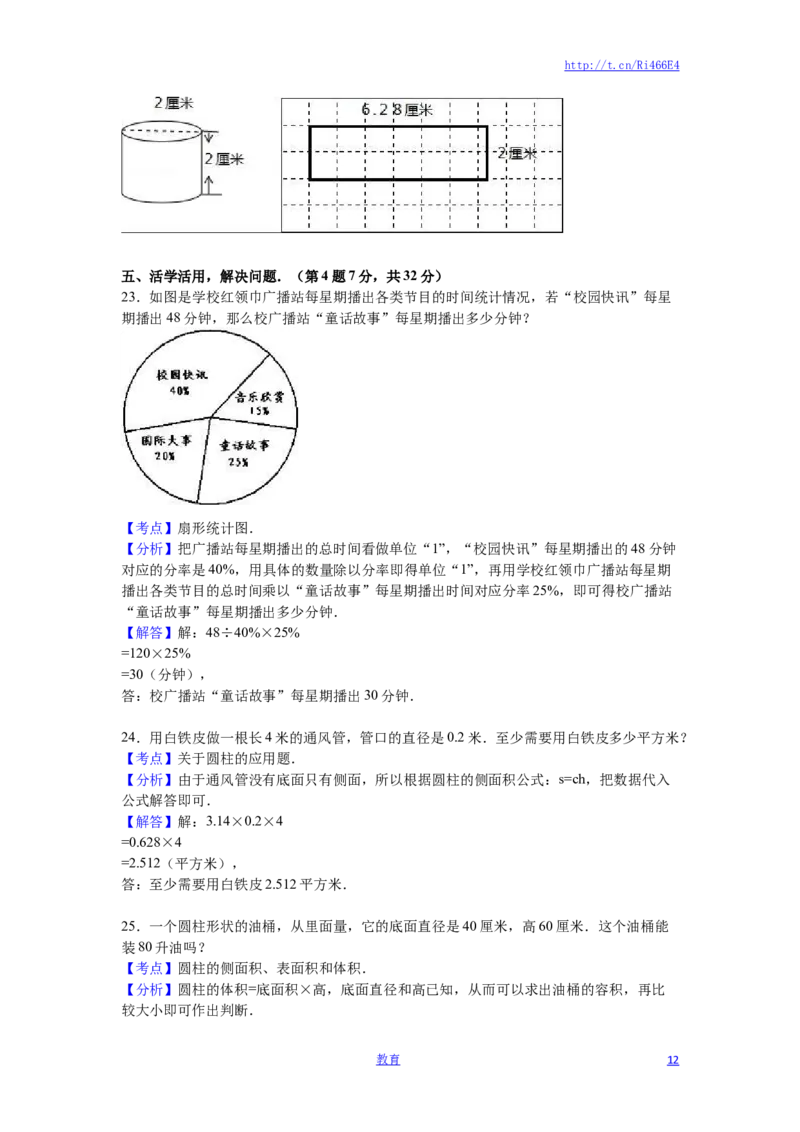
22.把下面的圆柱的侧面沿高展开,画出这个圆柱的侧面展开图,并写出相关计算过程.
(每一方格面积为1cm2)
【考点】圆柱的展开图.
【分析】圆柱由三部分组成:圆柱的侧面、圆柱的上、下两个底面;测量可知:该圆柱的
底面直径是2厘米,高为2厘米,根据“圆柱的侧面展开后是一个长方形,长方形的长等
于圆柱的底面周长,长方形的宽等于圆柱的高”可知:先根据圆的周长=πd,求出圆柱侧
面展开后的长方形的长,宽为圆柱的高;圆柱的上下两个底面为直径为2厘米的圆,画出
即可.
【解答】解:测量可知:圆柱的底面直径是2厘米,高为2厘米;
长方形的长:3.14×2=6.28(厘米),宽为2厘米;
画图如下:
教育 11http://t.cn/Ri466E4
五、活学活用,解决问题.(第4题7分,共32分)
23.如图是学校红领巾广播站每星期播出各类节目的时间统计情况,若“校园快讯”每星
期播出48分钟,那么校广播站“童话故事”每星期播出多少分钟?
【考点】扇形统计图.
【分析】把广播站每星期播出的总时间看做单位“1”,“校园快讯”每星期播出的48分钟
对应的分率是40%,用具体的数量除以分率即得单位“1”,再用学校红领巾广播站每星期
播出各类节目的总时间乘以“童话故事”每星期播出时间对应分率25%,即可得校广播站
“童话故事”每星期播出多少分钟.
【解答】解:48÷40%×25%
=120×25%
=30(分钟),
答:校广播站“童话故事”每星期播出30分钟.
24.用白铁皮做一根长4米的通风管,管口的直径是0.2米.至少需要用白铁皮多少平方米?
【考点】关于圆柱的应用题.
【分析】由于通风管没有底面只有侧面,所以根据圆柱的侧面积公式:s=ch,把数据代入
公式解答即可.
【解答】解:3.14×0.2×4
=0.628×4
=2.512(平方米),
答:至少需要用白铁皮2.512平方米.
25.一个圆柱形状的油桶,从里面量,它的底面直径是40厘米,高60厘米.这个油桶能
装80升油吗?
【考点】圆柱的侧面积、表面积和体积.
【分析】圆柱的体积=底面积×高,底面直径和高已知,从而可以求出油桶的容积,再比
较大小即可作出判断.
教育 12http://t.cn/Ri466E4
【解答】解:3.14×(40÷2)2×60
=3.14×400×60
=75360(立方厘米)
75360立方厘米=75.36升
因为75.36<80,所以这个油桶不能装80升油.
答:这个油桶不能装80升油.
26.一个圆柱形水池,从里面量,底面半径4米,深3.5米.水池的占地面积是多少平方米?
水池里最多能蓄水多少吨?(1立方米重1吨)
【考点】关于圆柱的应用题.
【分析】水池的占地面积等于这个圆柱的底面积,根据圆的面积公式:s=πr2,把数据代入
公式解答,再根据圆柱的容积(体积)公式:v=sh,把数据代入公式解答即可.
【解答】解:3.14×42
=3.14×16
=50.24(平方米),
50.24×3.5=175.84(立方米),
175.84×1=175.84(吨),
答:水池的占地面积是50.24平方米,水池里最多能蓄水175.84吨.
27.甲、乙两地间的铁路长350千米,一列客车和一列货车分别从甲乙两地同时出发相向
而行.货车的速度是客车的 ,相遇时客车和货车各行驶了多少千米?
【考点】分数除法应用题.
【分析】货车的速度是客车的 ,则相遇时,货车行了全程的 ,根据分数乘法的意义,
相遇时,货车行了350× 千米,然后用减法求出客车行了多少千米.
【解答】解:350× 150(千米)
350﹣150=200(千米)
答:相遇时客车行驶了200千米,货车行驶了150千米.
28.一个圆锥形沙堆,底面积是25平方米,高是1.2米.用这堆沙子去填一个长10米,宽
4米的长方体沙坑.沙坑里沙子的厚度是多少?
【考点】关于圆锥的应用题.
【分析】根据题意可知把圆锥形的沙堆填在长方体沙坑里,沙的体积不变,根据圆锥的体
积公式:v= sh,求出沙的体积,然后用沙的体积除以长方体沙坑的底面积即可.据此解
答.
【解答】解: ×25×1.2÷(10×4)
=10÷40
=9.6÷30
=0.25(米)
教育 13http://t.cn/Ri466E4
答:沙坑里沙子的厚度是0.25米.
教育 14http://t.cn/Ri466E4
2016年8月24日
教育 15