文档内容
2020年湖南省湘潭市中考数学试卷
一、选择题(本大题共8小题,每小题有且只有一个正确答案,请将正确答案的选项代号涂在
答题卡相应的位置上,每小题3分,满分24分)
1.(3分)﹣6的绝对值是( )
A.﹣6 B.6 C.﹣ D.
2.(3分)地摊经济一词最近彻底火了,发展地摊经济,进行室外经营与有序占道经营,能满
足民众消费需求,在一定程度上缓解了就业压力,带动了第三产业发展,同时活跃市场,
刺激经济发展,一经推出,相关微博话题阅读量就超过了600000000次,这个数据用科学
记数法表示为( )
A.0.6×108 B.6×107 C.6×108 D.6×109
3.(3分)已知2xn+1y3与 x4y3是同类项,则n的值是( )
A.2 B.3 C.4 D.5
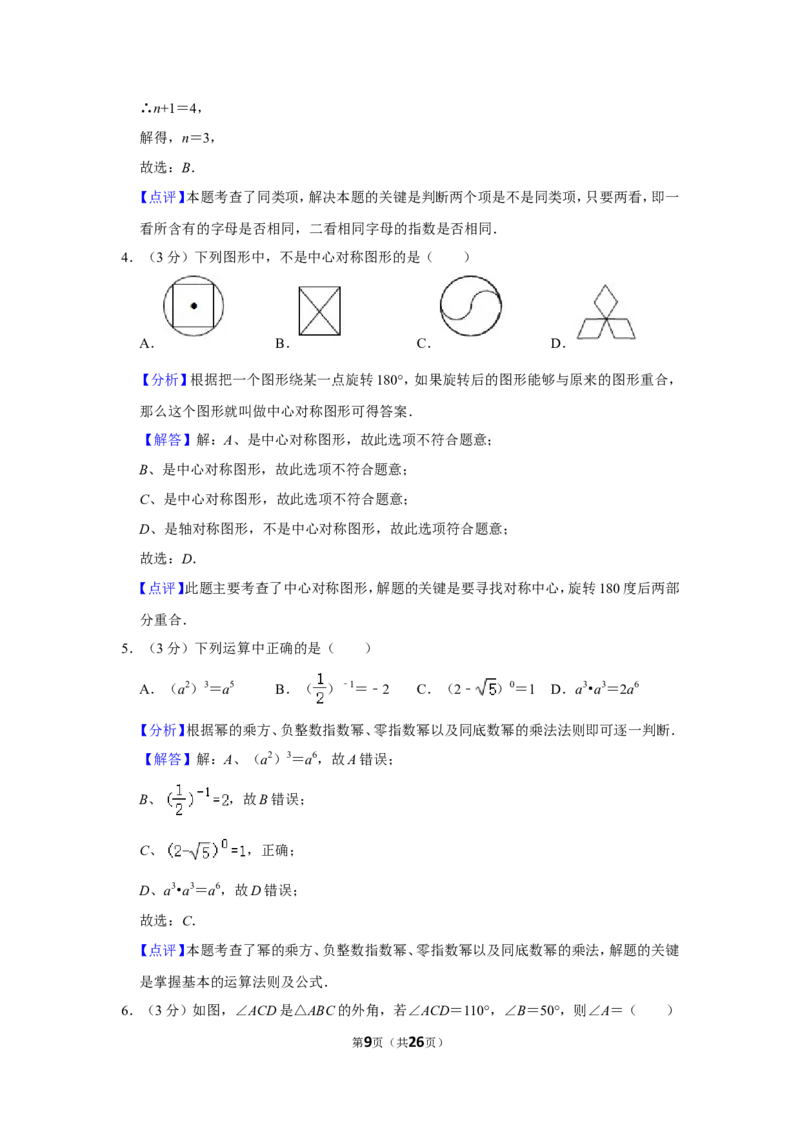
4.(3分)下列图形中,不是中心对称图形的是( )
A. B. C. D.
5.(3分)下列运算中正确的是( )
A.(a2)3=a5 B.( )﹣1=﹣2 C.(2﹣ )0=1 D.a3•a3=2a6
6.(3分)如图,∠ACD是△ABC的外角,若∠ACD=110°,∠B=50°,则∠A=( )
A.40° B.50° C.55° D.60°
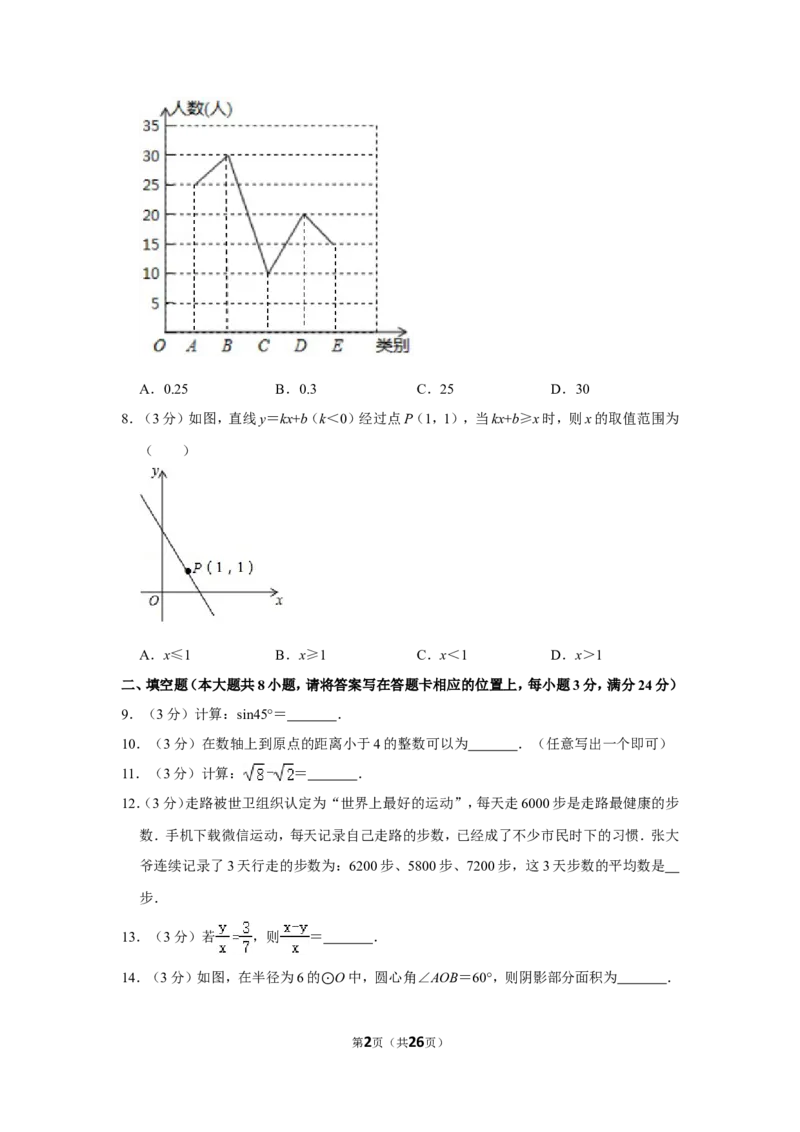
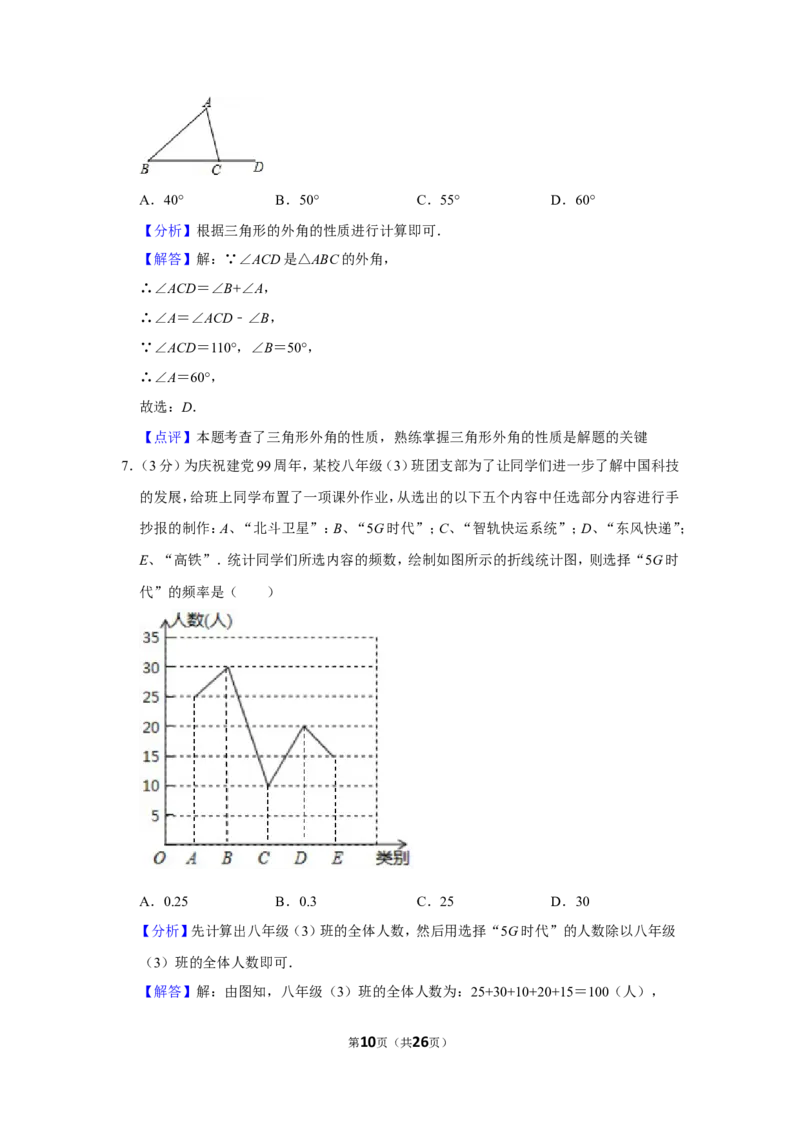
7.(3分)为庆祝建党99周年,某校八年级(3)班团支部为了让同学们进一步了解中国科技
的发展,给班上同学布置了一项课外作业,从选出的以下五个内容中任选部分内容进行手
抄报的制作:A、“北斗卫星”:B、“5G时代”;C、“智轨快运系统”;D、“东风快递”;
E、“高铁”.统计同学们所选内容的频数,绘制如图所示的折线统计图,则选择“5G时
代”的频率是( )
第1页(共26页)A.0.25 B.0.3 C.25 D.30
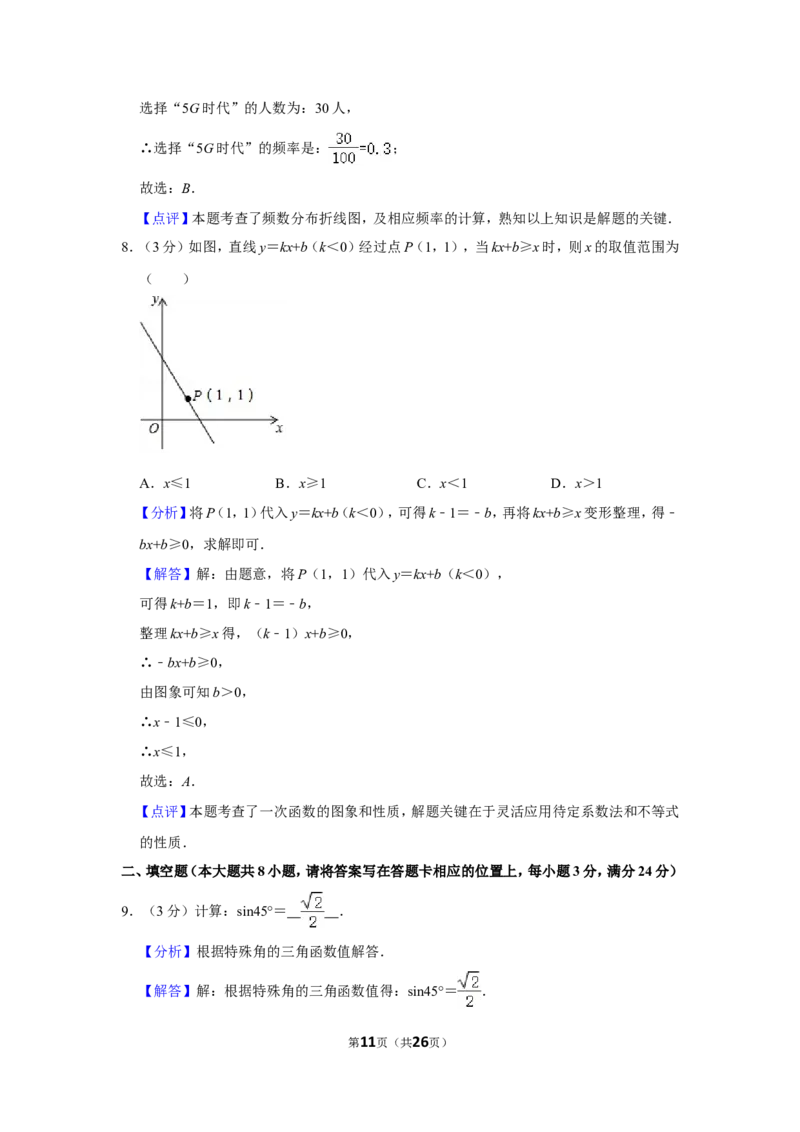
8.(3分)如图,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,则x的取值范围为
( )
A.x≤1 B.x≥1 C.x<1 D.x>1
二、填空题(本大题共8小题,请将答案写在答题卡相应的位置上,每小题3分,满分24分)
9.(3分)计算:sin45°= .
10.(3分)在数轴上到原点的距离小于4的整数可以为 .(任意写出一个即可)
11.(3分)计算: = .
12.(3分)走路被世卫组织认定为“世界上最好的运动”,每天走6000步是走路最健康的步
数.手机下载微信运动,每天记录自己走路的步数,已经成了不少市民时下的习惯.张大
爷连续记录了3天行走的步数为:6200步、5800步、7200步,这3天步数的平均数是
步.
13.(3分)若 ,则 = .
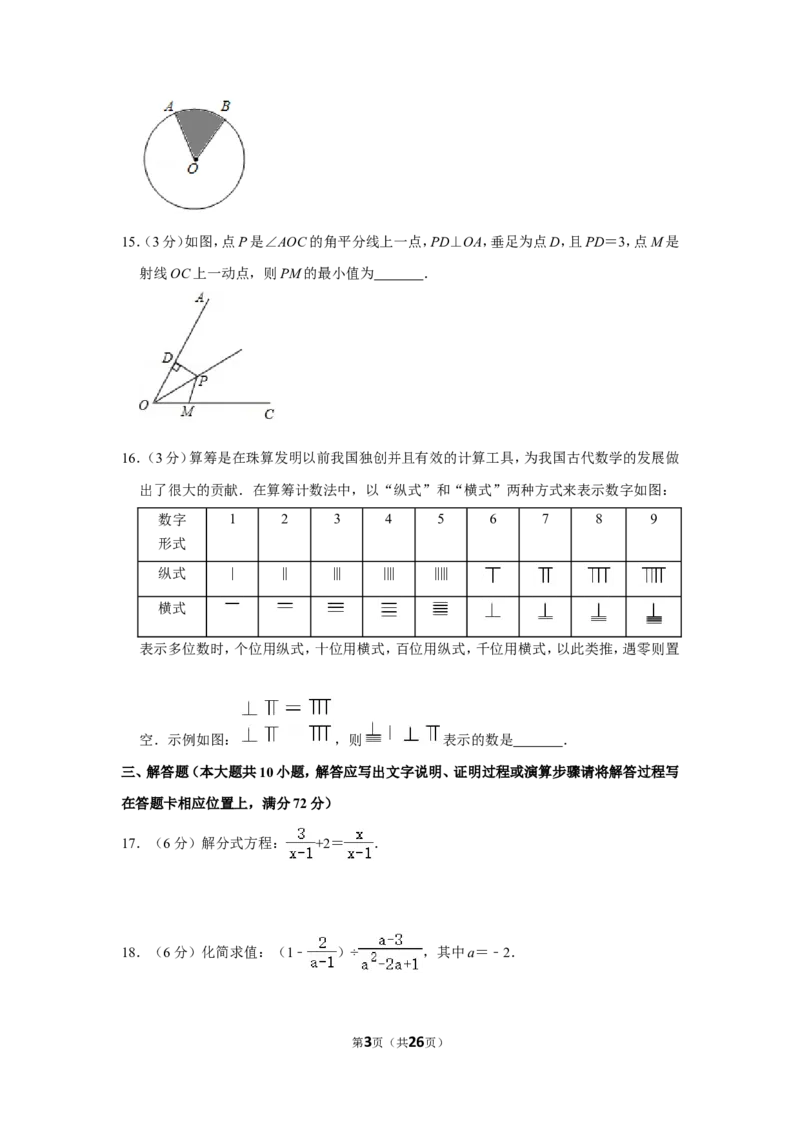
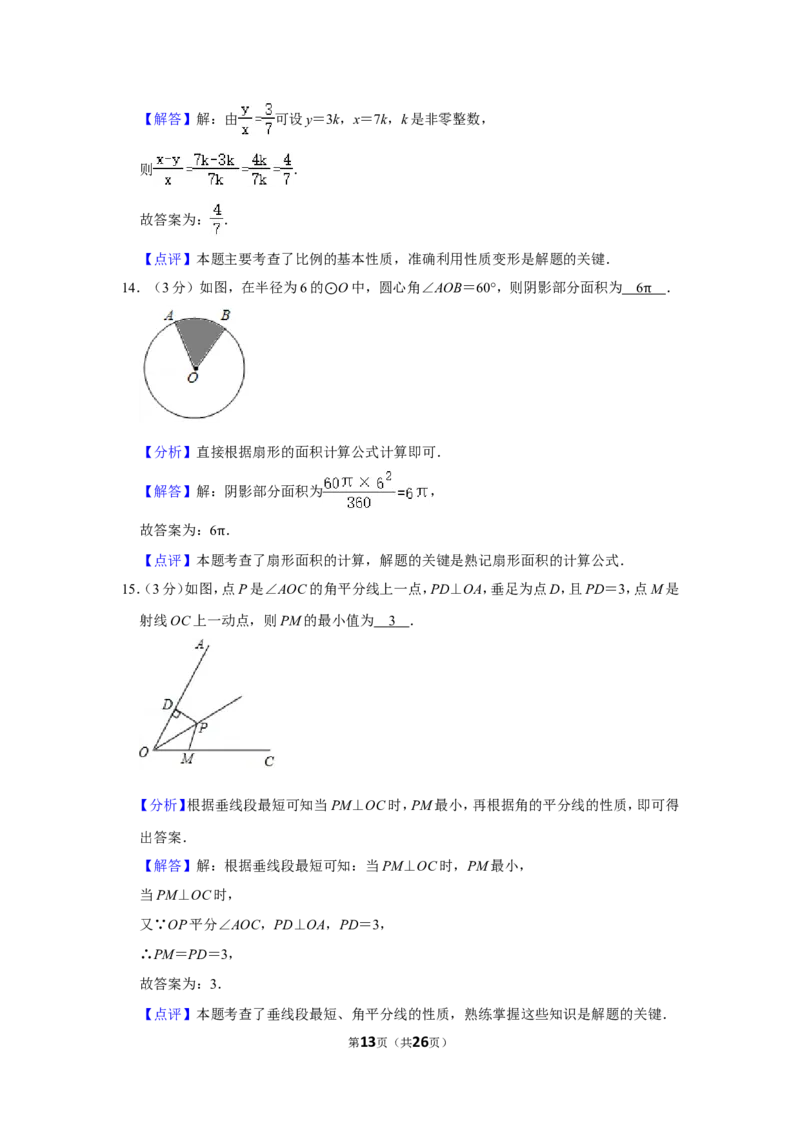
14.(3分)如图,在半径为6的 O中,圆心角∠AOB=60°,则阴影部分面积为 .
⊙
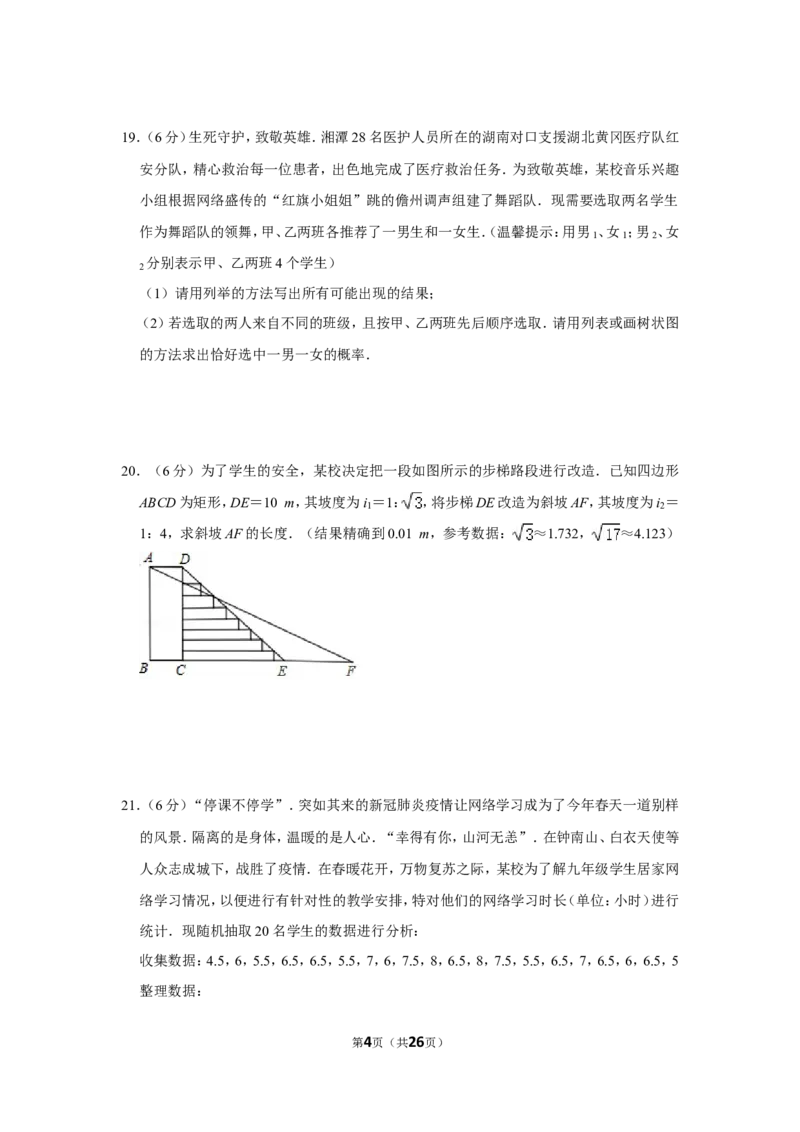
第2页(共26页)15.(3分)如图,点P是∠AOC的角平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是
射线OC上一动点,则PM的最小值为 .
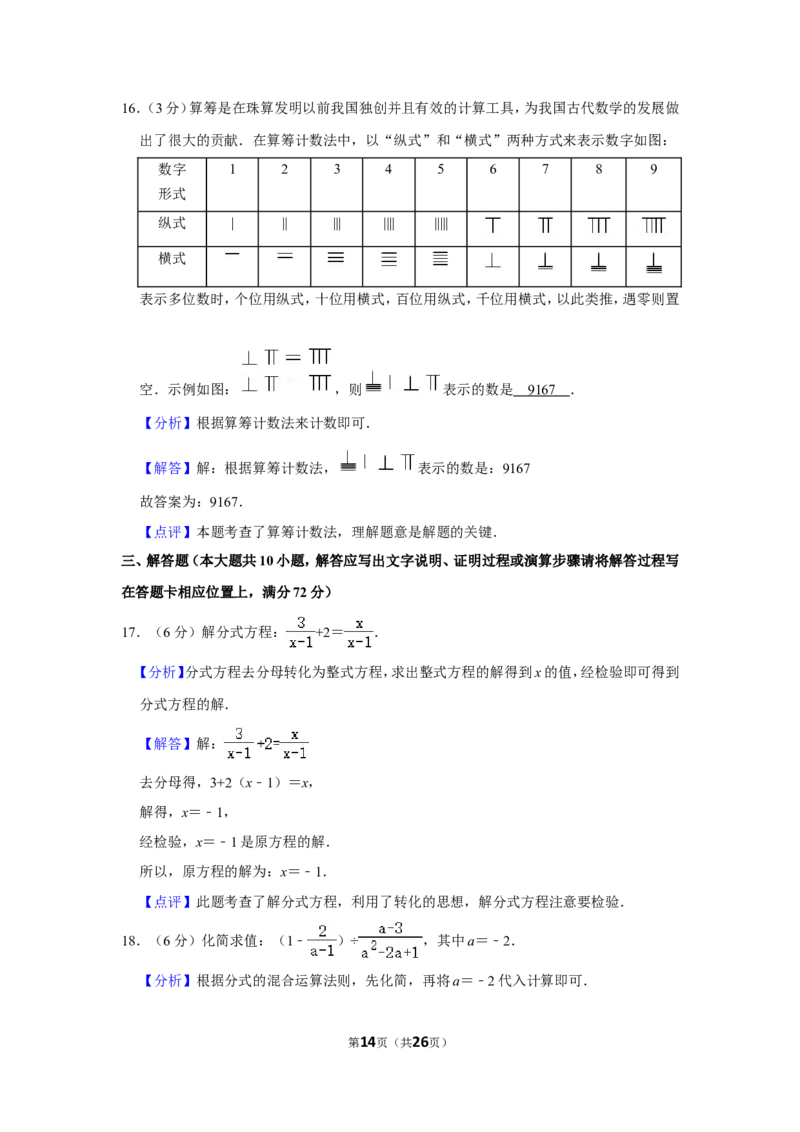
16.(3分)算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做
出了很大的贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字如图:
数字 1 2 3 4 5 6 7 8 9
形式
纵式 | || ||| |||| |||||
横式
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置
空.示例如图: ,则 表示的数是 .
三、解答题(本大题共10小题,解答应写出文字说明、证明过程或演算步骤请将解答过程写
在答题卡相应位置上,满分72分)
17.(6分)解分式方程: +2= .
18.(6分)化简求值:(1﹣ )÷ ,其中a=﹣2.
第3页(共26页)19.(6分)生死守护,致敬英雄.湘潭28名医护人员所在的湖南对口支援湖北黄冈医疗队红
安分队,精心救治每一位患者,出色地完成了医疗救治任务.为致敬英雄,某校音乐兴趣
小组根据网络盛传的“红旗小姐姐”跳的儋州调声组建了舞蹈队.现需要选取两名学生
作为舞蹈队的领舞,甲、乙两班各推荐了一男生和一女生.(温馨提示:用男 、女 ;男 、女
1 1 2
分别表示甲、乙两班4个学生)
2
(1)请用列举的方法写出所有可能出现的结果;
(2)若选取的两人来自不同的班级,且按甲、乙两班先后顺序选取.请用列表或画树状图
的方法求出恰好选中一男一女的概率.
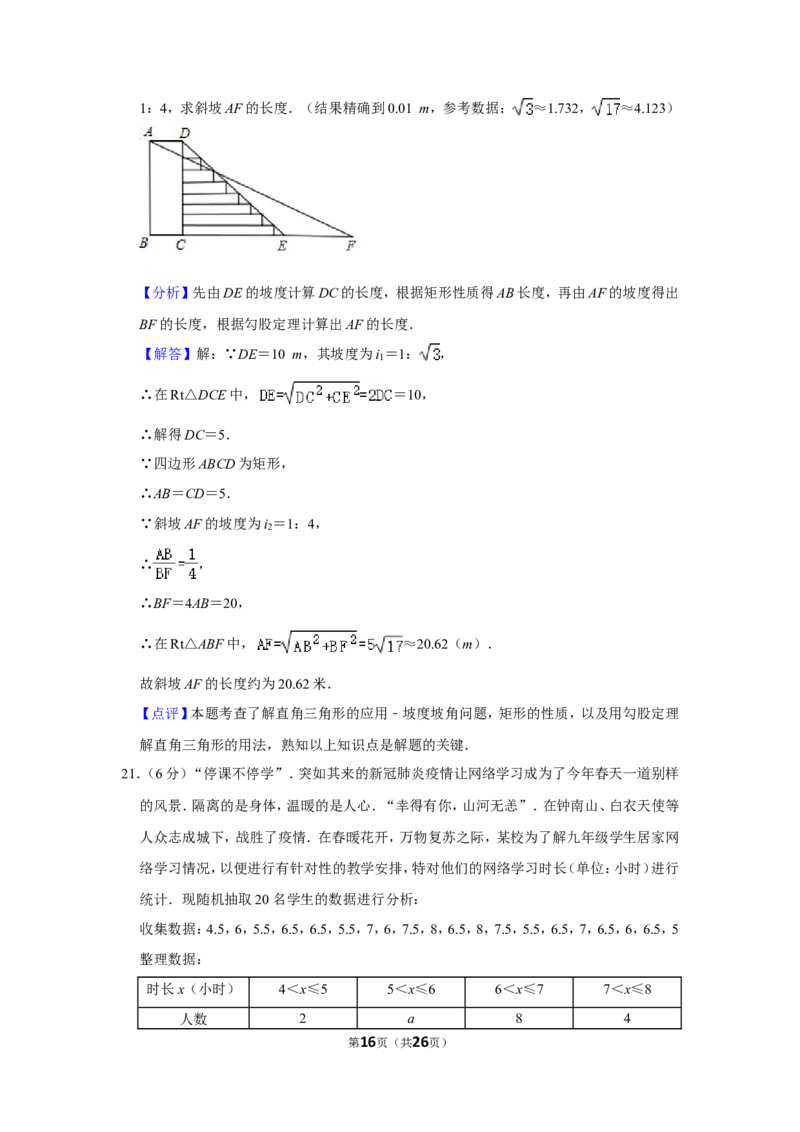
20.(6分)为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形
ABCD为矩形,DE=10 m,其坡度为i =1: ,将步梯DE改造为斜坡AF,其坡度为i =
1 2
1:4,求斜坡AF的长度.(结果精确到0.01 m,参考数据: ≈1.732, ≈4.123)
21.(6分)“停课不停学”.突如其来的新冠肺炎疫情让网络学习成为了今年春天一道别样
的风景.隔离的是身体,温暖的是人心.“幸得有你,山河无恙”.在钟南山、白衣天使等
人众志成城下,战胜了疫情.在春暖花开,万物复苏之际,某校为了解九年级学生居家网
络学习情况,以便进行有针对性的教学安排,特对他们的网络学习时长(单位:小时)进行
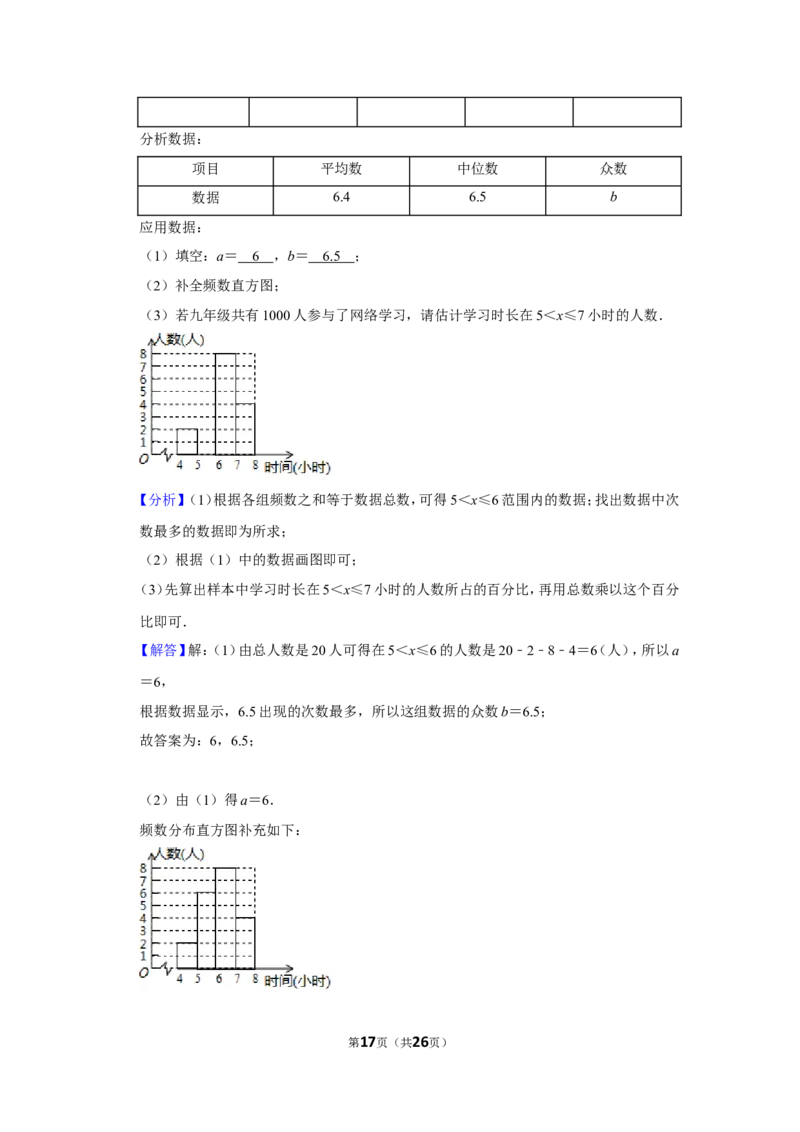
统计.现随机抽取20名学生的数据进行分析:
收集数据:4.5,6,5.5,6.5,6.5,5.5,7,6,7.5,8,6.5,8,7.5,5.5,6.5,7,6.5,6,6.5,5
整理数据:
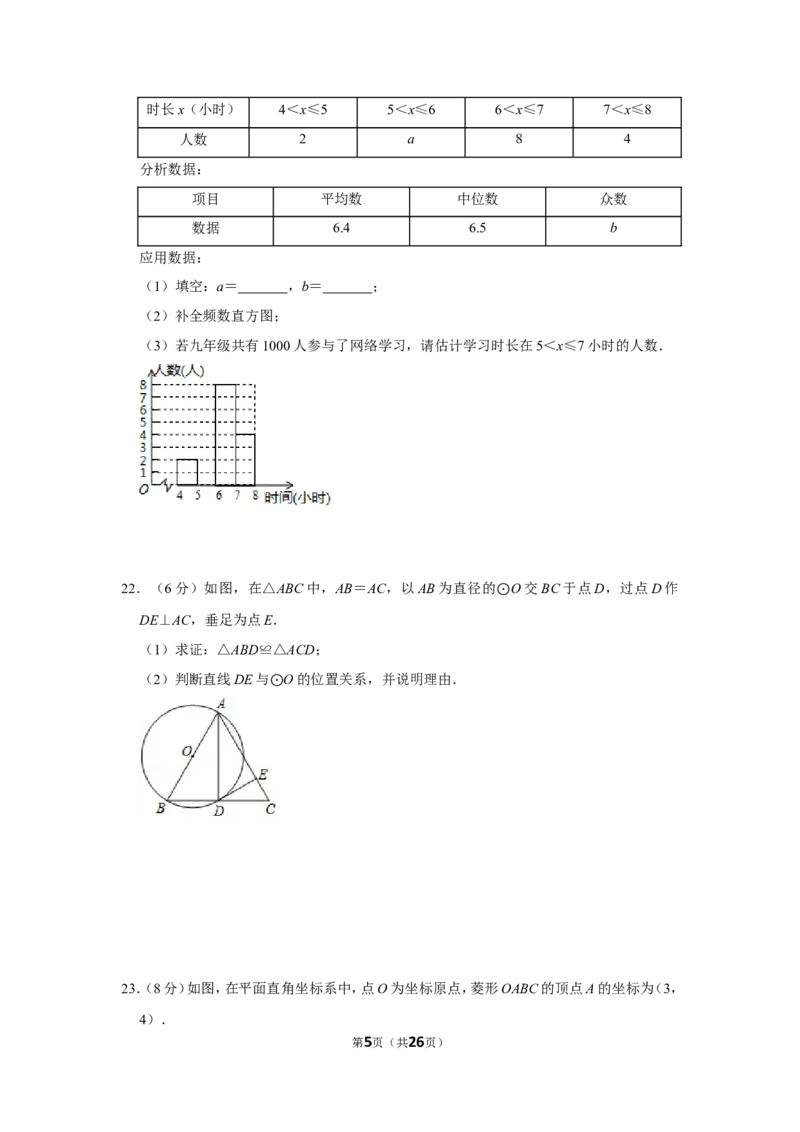
第4页(共26页)时长x(小时) 4<x≤5 5<x≤6 6<x≤7 7<x≤8
人数 2 a 8 4
分析数据:
项目 平均数 中位数 众数
数据 6.4 6.5 b
应用数据:
(1)填空:a= ,b= ;
(2)补全频数直方图;
(3)若九年级共有1000人参与了网络学习,请估计学习时长在5<x≤7小时的人数.
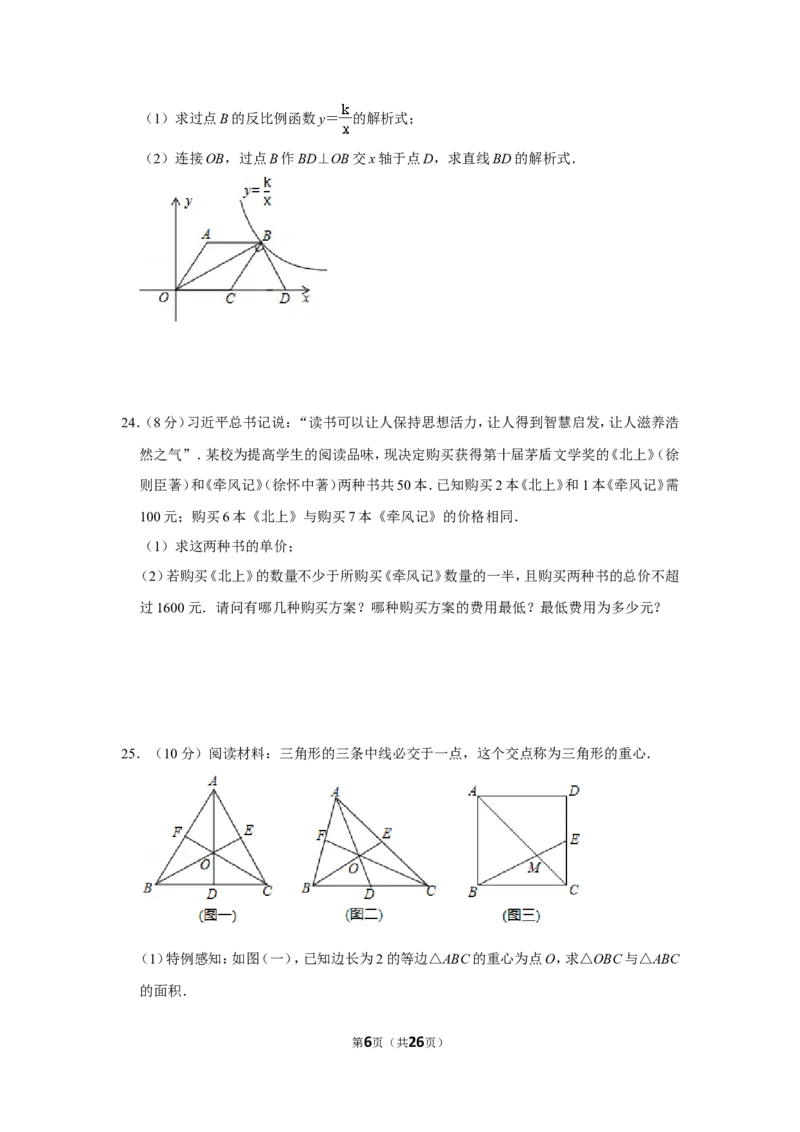
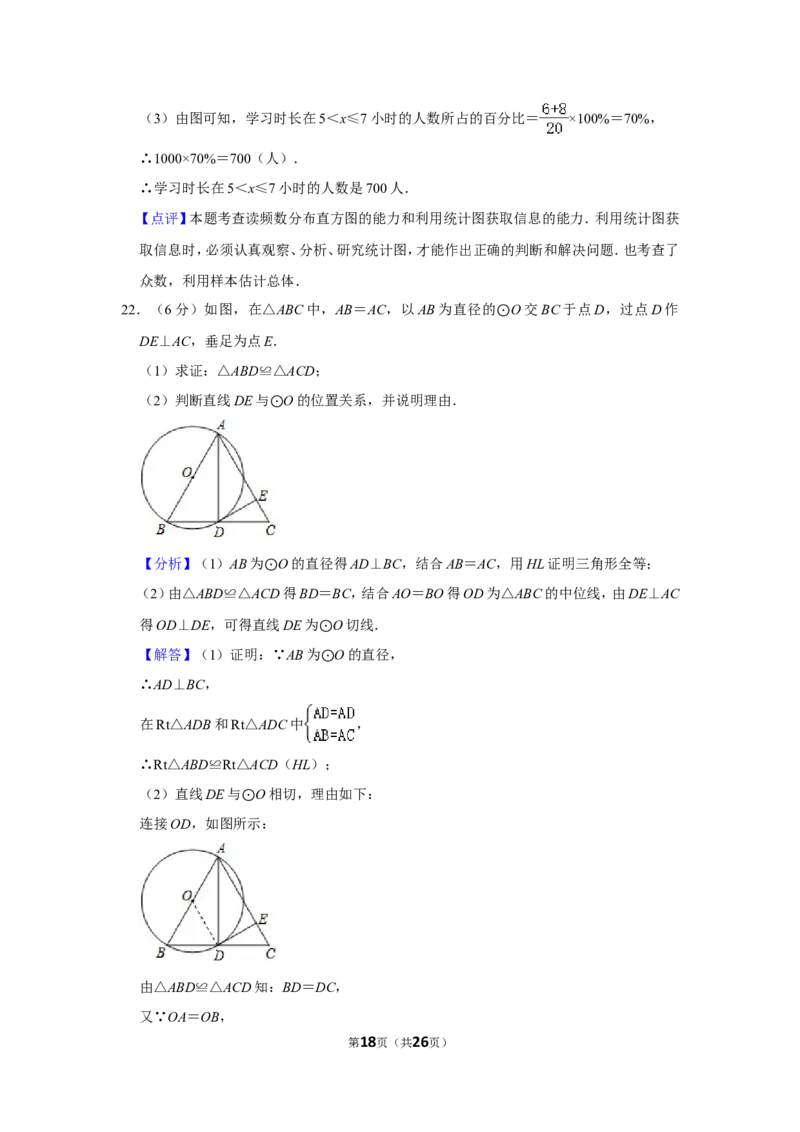
22.(6分)如图,在△ABC中,AB=AC,以AB为直径的 O交BC于点D,过点D作
DE⊥AC,垂足为点E. ⊙
(1)求证:△ABD≌△ACD;
(2)判断直线DE与 O的位置关系,并说明理由.
⊙
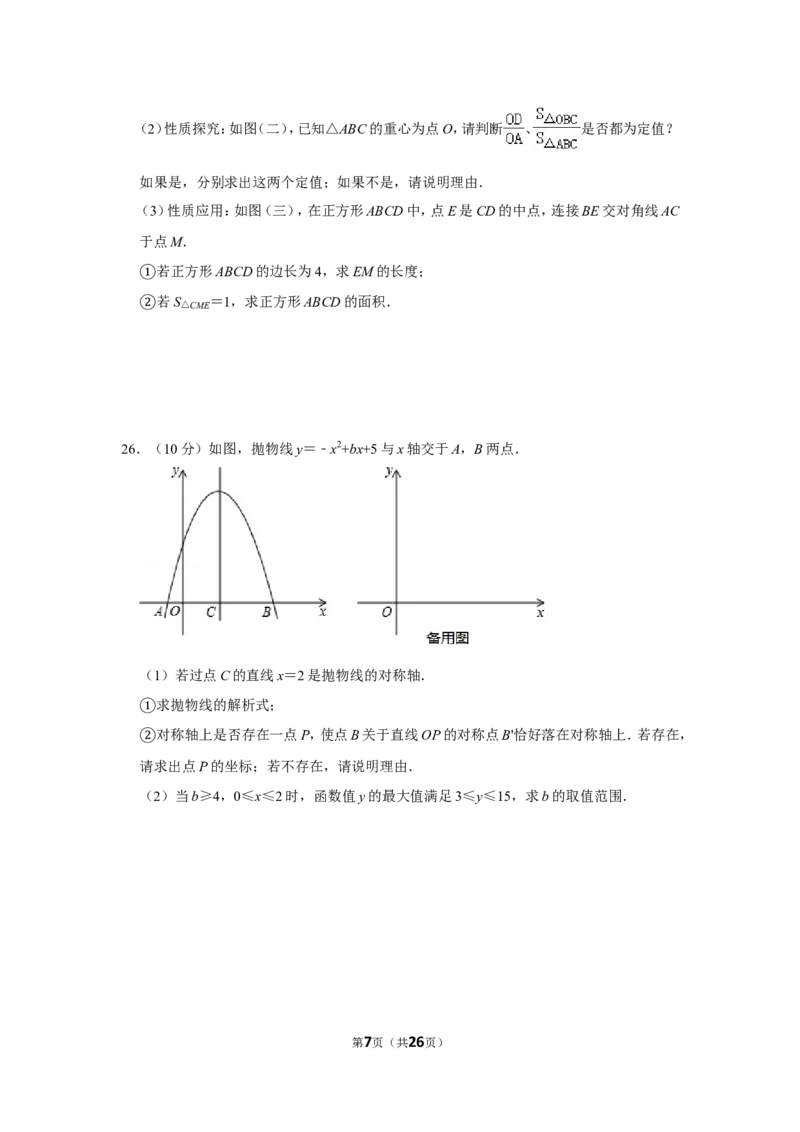
23.(8分)如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A的坐标为(3,
4).
第5页(共26页)(1)求过点B的反比例函数y= 的解析式;
(2)连接OB,过点B作BD⊥OB交x轴于点D,求直线BD的解析式.
24.(8分)习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩
然之气”.某校为提高学生的阅读品味,现决定购买获得第十届茅盾文学奖的《北上》(徐
则臣著)和《牵风记》(徐怀中著)两种书共50本.已知购买2本《北上》和1本《牵风记》需
100元;购买6本《北上》与购买7本《牵风记》的价格相同.
(1)求这两种书的单价;
(2)若购买《北上》的数量不少于所购买《牵风记》数量的一半,且购买两种书的总价不超
过1600元.请问有哪几种购买方案?哪种购买方案的费用最低?最低费用为多少元?
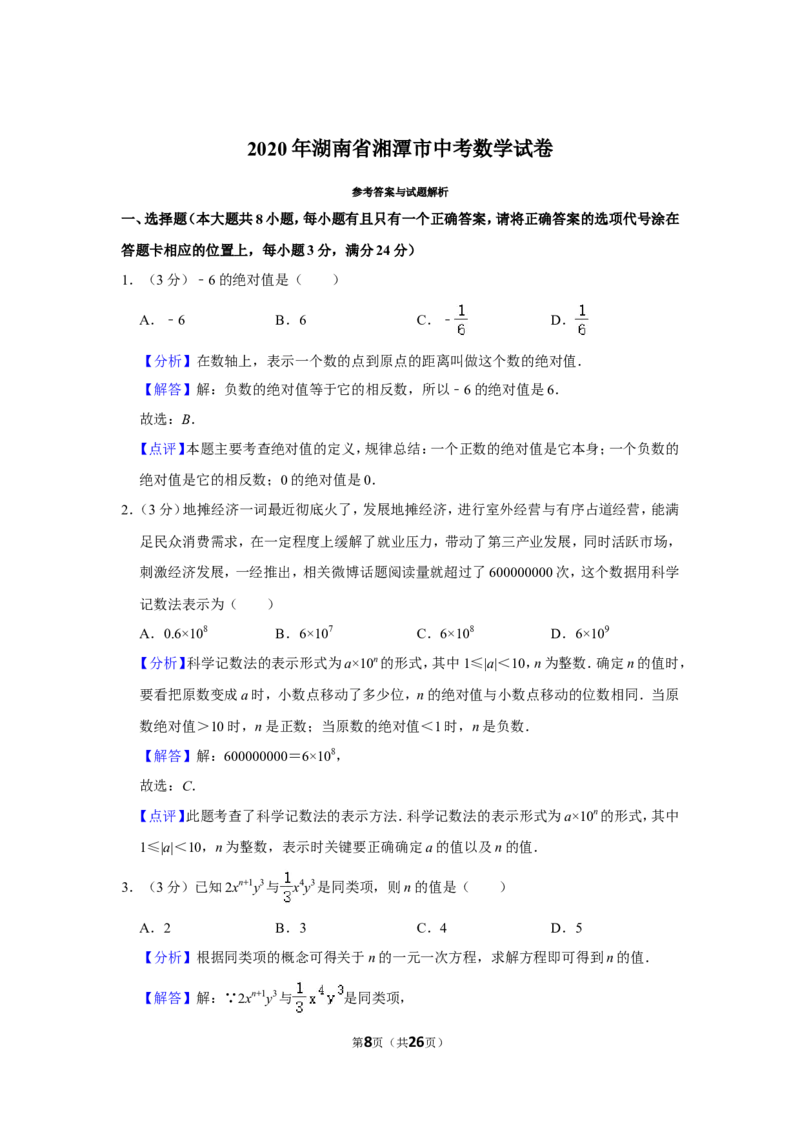
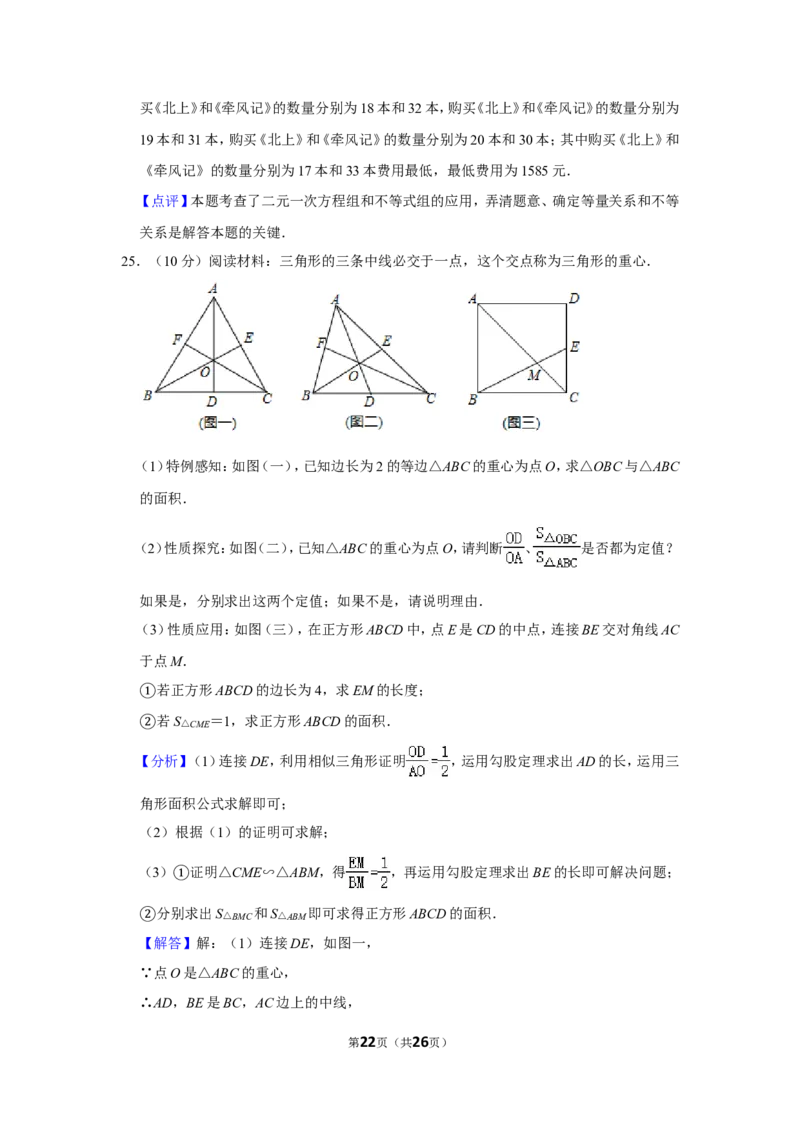
25.(10分)阅读材料:三角形的三条中线必交于一点,这个交点称为三角形的重心.
(1)特例感知:如图(一),已知边长为2的等边△ABC的重心为点O,求△OBC与△ABC
的面积.
第6页(共26页)(2)性质探究:如图(二),已知△ABC的重心为点O,请判断 、 是否都为定值?
如果是,分别求出这两个定值;如果不是,请说明理由.
(3)性质应用:如图(三),在正方形ABCD中,点E是CD的中点,连接BE交对角线AC
于点M.
若正方形ABCD的边长为4,求EM的长度;
①若S△CME =1,求正方形ABCD的面积.
②
26.(10分)如图,抛物线y=﹣x2+bx+5与x轴交于A,B两点.
(1)若过点C的直线x=2是抛物线的对称轴.
求抛物线的解析式;
①对称轴上是否存在一点P,使点B关于直线OP的对称点B'恰好落在对称轴上.若存在,
②请求出点P的坐标;若不存在,请说明理由.
(2)当b≥4,0≤x≤2时,函数值y的最大值满足3≤y≤15,求b的取值范围.
第7页(共26页)2020年湖南省湘潭市中考数学试卷
参考答案与试题解析
一、选择题(本大题共8小题,每小题有且只有一个正确答案,请将正确答案的选项代号涂在
答题卡相应的位置上,每小题3分,满分24分)
1.(3分)﹣6的绝对值是( )
A.﹣6 B.6 C.﹣ D.
【分析】在数轴上,表示一个数的点到原点的距离叫做这个数的绝对值.
【解答】解:负数的绝对值等于它的相反数,所以﹣6的绝对值是6.
故选:B.
【点评】本题主要考查绝对值的定义,规律总结:一个正数的绝对值是它本身;一个负数的
绝对值是它的相反数;0的绝对值是0.
2.(3分)地摊经济一词最近彻底火了,发展地摊经济,进行室外经营与有序占道经营,能满
足民众消费需求,在一定程度上缓解了就业压力,带动了第三产业发展,同时活跃市场,
刺激经济发展,一经推出,相关微博话题阅读量就超过了600000000次,这个数据用科学
记数法表示为( )
A.0.6×108 B.6×107 C.6×108 D.6×109
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,
要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原
数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
【解答】解:600000000=6×108,
故选:C.
【点评】此题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中
1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3.(3分)已知2xn+1y3与 x4y3是同类项,则n的值是( )
A.2 B.3 C.4 D.5
【分析】根据同类项的概念可得关于n的一元一次方程,求解方程即可得到n的值.
【解答】解:∵2xn+1y3与 是同类项,
第8页(共26页)∴n+1=4,
解得,n=3,
故选:B.
【点评】本题考查了同类项,解决本题的关键是判断两个项是不是同类项,只要两看,即一
看所含有的字母是否相同,二看相同字母的指数是否相同.
4.(3分)下列图形中,不是中心对称图形的是( )
A. B. C. D.
【分析】根据把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,
那么这个图形就叫做中心对称图形可得答案.
【解答】解:A、是中心对称图形,故此选项不符合题意;
B、是中心对称图形,故此选项不符合题意;
C、是中心对称图形,故此选项不符合题意;
D、是轴对称图形,不是中心对称图形,故此选项符合题意;
故选:D.
【点评】此题主要考查了中心对称图形,解题的关键是要寻找对称中心,旋转180度后两部
分重合.
5.(3分)下列运算中正确的是( )
A.(a2)3=a5 B.( )﹣1=﹣2 C.(2﹣ )0=1 D.a3•a3=2a6
【分析】根据幂的乘方、负整数指数幂、零指数幂以及同底数幂的乘法法则即可逐一判断.
【解答】解:A、(a2)3=a6,故A错误;
B、 ,故B错误;
C、 ,正确;
D、a3•a3=a6,故D错误;
故选:C.
【点评】本题考查了幂的乘方、负整数指数幂、零指数幂以及同底数幂的乘法,解题的关键
是掌握基本的运算法则及公式.
6.(3分)如图,∠ACD是△ABC的外角,若∠ACD=110°,∠B=50°,则∠A=( )
第9页(共26页)A.40° B.50° C.55° D.60°
【分析】根据三角形的外角的性质进行计算即可.
【解答】解:∵∠ACD是△ABC的外角,
∴∠ACD=∠B+∠A,
∴∠A=∠ACD﹣∠B,
∵∠ACD=110°,∠B=50°,
∴∠A=60°,
故选:D.
【点评】本题考查了三角形外角的性质,熟练掌握三角形外角的性质是解题的关键
7.(3分)为庆祝建党99周年,某校八年级(3)班团支部为了让同学们进一步了解中国科技
的发展,给班上同学布置了一项课外作业,从选出的以下五个内容中任选部分内容进行手
抄报的制作:A、“北斗卫星”:B、“5G时代”;C、“智轨快运系统”;D、“东风快递”;
E、“高铁”.统计同学们所选内容的频数,绘制如图所示的折线统计图,则选择“5G时
代”的频率是( )
A.0.25 B.0.3 C.25 D.30
【分析】先计算出八年级(3)班的全体人数,然后用选择“5G时代”的人数除以八年级
(3)班的全体人数即可.
【解答】解:由图知,八年级(3)班的全体人数为:25+30+10+20+15=100(人),
第10页(共26页)选择“5G时代”的人数为:30人,
∴选择“5G时代”的频率是: ;
故选:B.
【点评】本题考查了频数分布折线图,及相应频率的计算,熟知以上知识是解题的关键.
8.(3分)如图,直线y=kx+b(k<0)经过点P(1,1),当kx+b≥x时,则x的取值范围为
( )
A.x≤1 B.x≥1 C.x<1 D.x>1
【分析】将P(1,1)代入y=kx+b(k<0),可得k﹣1=﹣b,再将kx+b≥x变形整理,得﹣
bx+b≥0,求解即可.
【解答】解:由题意,将P(1,1)代入y=kx+b(k<0),
可得k+b=1,即k﹣1=﹣b,
整理kx+b≥x得,(k﹣1)x+b≥0,
∴﹣bx+b≥0,
由图象可知b>0,
∴x﹣1≤0,
∴x≤1,
故选:A.
【点评】本题考查了一次函数的图象和性质,解题关键在于灵活应用待定系数法和不等式
的性质.
二、填空题(本大题共8小题,请将答案写在答题卡相应的位置上,每小题3分,满分24分)
9.(3分)计算:sin45°= .
【分析】根据特殊角的三角函数值解答.
【解答】解:根据特殊角的三角函数值得:sin45°= .
第11页(共26页)【点评】本题考查特殊角三角函数值的计算,特殊角三角函数值计算在中考中经常出现,
题型以选择题、填空题为主.
【相关链接】特殊角三角函数值:
sin30°= ,cos30°= ,tan30°= ,cot30°= ;
sin45°= ,cos45°= ,tan45°=1,cot45°=1;
sin60°= ,cos60°= ,tan60°= ,cot60°= .
10.(3分)在数轴上到原点的距离小于4的整数可以为 3 .(任意写出一个即可)
【分析】根据数轴表示数的意义,可得出答案为±3,±2,±1,0中任意写出一个即可.
【解答】解:在数轴上到原点的距离小于4的整数有:﹣3,3,﹣2,2,﹣1,1,0从中任选一
个即可
故答案为:3(答案不唯一,3,2,1,0,﹣1,﹣2,﹣3任意一个均可);
【点评】本题考查了数轴、绝对值等知识,熟练掌握这些知识是解题的关键.
11.(3分)计算: = .
【分析】先把 化简为2 ,再合并同类二次根式即可得解.
【解答】解: =2 ﹣ = .
故答案为 .
【点评】本题考查了二次根式的运算,正确对二次根式进行化简是关键.
12.(3分)走路被世卫组织认定为“世界上最好的运动”,每天走6000步是走路最健康的步
数.手机下载微信运动,每天记录自己走路的步数,已经成了不少市民时下的习惯.张大
爷连续记录了3天行走的步数为:6200步、5800步、7200步,这3天步数的平均数是
6400 步.
【分析】根据算术平均数的计算公式即可解答.
【解答】解:这3天步数的平均数是: (步),
故答案为:6400.
【点评】本题考查了平均数的计算,解题的关键是掌握平均数的计算公式.
13.(3分)若 ,则 = .
【分析】根据比例的基本性质变形,代入求值即可.
第12页(共26页)【解答】解:由 可设y=3k,x=7k,k是非零整数,
则 .
故答案为: .
【点评】本题主要考查了比例的基本性质,准确利用性质变形是解题的关键.
14.(3分)如图,在半径为6的 O中,圆心角∠AOB=60°,则阴影部分面积为 6 .
⊙ π
【分析】直接根据扇形的面积计算公式计算即可.
【解答】解:阴影部分面积为 ,
故答案为:6 .
【点评】本题π考查了扇形面积的计算,解题的关键是熟记扇形面积的计算公式.
15.(3分)如图,点P是∠AOC的角平分线上一点,PD⊥OA,垂足为点D,且PD=3,点M是
射线OC上一动点,则PM的最小值为 3 .
【分析】根据垂线段最短可知当PM⊥OC时,PM最小,再根据角的平分线的性质,即可得
出答案.
【解答】解:根据垂线段最短可知:当PM⊥OC时,PM最小,
当PM⊥OC时,
又∵OP平分∠AOC,PD⊥OA,PD=3,
∴PM=PD=3,
故答案为:3.
【点评】本题考查了垂线段最短、角平分线的性质,熟练掌握这些知识是解题的关键.
第13页(共26页)16.(3分)算筹是在珠算发明以前我国独创并且有效的计算工具,为我国古代数学的发展做
出了很大的贡献.在算筹计数法中,以“纵式”和“横式”两种方式来表示数字如图:
数字 1 2 3 4 5 6 7 8 9
形式
纵式 | || ||| |||| |||||
横式
表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置
空.示例如图: ,则 表示的数是 916 7 .
【分析】根据算筹计数法来计数即可.
【解答】解:根据算筹计数法, 表示的数是:9167
故答案为:9167.
【点评】本题考查了算筹计数法,理解题意是解题的关键.
三、解答题(本大题共10小题,解答应写出文字说明、证明过程或演算步骤请将解答过程写
在答题卡相应位置上,满分72分)
17.(6分)解分式方程: +2= .
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到
分式方程的解.
【解答】解:
去分母得,3+2(x﹣1)=x,
解得,x=﹣1,
经检验,x=﹣1是原方程的解.
所以,原方程的解为:x=﹣1.
【点评】此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.
18.(6分)化简求值:(1﹣ )÷ ,其中a=﹣2.
【分析】根据分式的混合运算法则,先化简,再将a=﹣2代入计算即可.
第14页(共26页)【解答】解:
=
=a﹣1,
将a=﹣2代入得:原式=﹣2﹣1=﹣3.
【点评】本题主要考查分式的化简求值,解题的关键是熟练掌握分式的混合运算顺序和运
算法则.
19.(6分)生死守护,致敬英雄.湘潭28名医护人员所在的湖南对口支援湖北黄冈医疗队红
安分队,精心救治每一位患者,出色地完成了医疗救治任务.为致敬英雄,某校音乐兴趣
小组根据网络盛传的“红旗小姐姐”跳的儋州调声组建了舞蹈队.现需要选取两名学生
作为舞蹈队的领舞,甲、乙两班各推荐了一男生和一女生.(温馨提示:用男 、女 ;男 、女
1 1 2
分别表示甲、乙两班4个学生)
2
(1)请用列举的方法写出所有可能出现的结果;
(2)若选取的两人来自不同的班级,且按甲、乙两班先后顺序选取.请用列表或画树状图
的方法求出恰好选中一男一女的概率.
【分析】(1)直接列举出所有可能出现的结果即可;
(2)列出表格,找出符合题意的可能结果,再利用概率公式求出概率即可.
【解答】解:(1)可能出现的结果有:男 女 、男 男 、男 女 、男 女 、男 女 、女 女 ;
1 1 1 2 1 2 2 1 2 2 1 2
(2)列表法表示所有可能出现的结果如下:
共有4种情况,其中恰好选中一男一女有2种情况,
所以恰好选中一男一女的概率为 .
【点评】本题考查列举法和树状图法,注意结合题意中“写出所有可能的结果”的要求,
使用列举法,注意按一定的顺序列举,做到不重不漏.
20.(6分)为了学生的安全,某校决定把一段如图所示的步梯路段进行改造.已知四边形
ABCD为矩形,DE=10 m,其坡度为i =1: ,将步梯DE改造为斜坡AF,其坡度为i =
1 2
第15页(共26页)1:4,求斜坡AF的长度.(结果精确到0.01 m,参考数据: ≈1.732, ≈4.123)
【分析】先由DE的坡度计算DC的长度,根据矩形性质得AB长度,再由AF的坡度得出
BF的长度,根据勾股定理计算出AF的长度.
【解答】解:∵DE=10 m,其坡度为i =1: ,
1
∴在Rt△DCE中, =10,
∴解得DC=5.
∵四边形ABCD为矩形,
∴AB=CD=5.
∵斜坡AF的坡度为i =1:4,
2
∴ ,
∴BF=4AB=20,
∴在Rt△ABF中, ≈20.62(m).
故斜坡AF的长度约为20.62米.
【点评】本题考查了解直角三角形的应用﹣坡度坡角问题,矩形的性质,以及用勾股定理
解直角三角形的用法,熟知以上知识点是解题的关键.
21.(6分)“停课不停学”.突如其来的新冠肺炎疫情让网络学习成为了今年春天一道别样
的风景.隔离的是身体,温暖的是人心.“幸得有你,山河无恙”.在钟南山、白衣天使等
人众志成城下,战胜了疫情.在春暖花开,万物复苏之际,某校为了解九年级学生居家网
络学习情况,以便进行有针对性的教学安排,特对他们的网络学习时长(单位:小时)进行
统计.现随机抽取20名学生的数据进行分析:
收集数据:4.5,6,5.5,6.5,6.5,5.5,7,6,7.5,8,6.5,8,7.5,5.5,6.5,7,6.5,6,6.5,5
整理数据:
时长x(小时) 4<x≤5 5<x≤6 6<x≤7 7<x≤8
人数 2 a 8 4
第16页(共26页)分析数据:
项目 平均数 中位数 众数
数据 6.4 6.5 b
应用数据:
(1)填空:a= 6 ,b= 6. 5 ;
(2)补全频数直方图;
(3)若九年级共有1000人参与了网络学习,请估计学习时长在5<x≤7小时的人数.
【分析】(1)根据各组频数之和等于数据总数,可得5<x≤6范围内的数据;找出数据中次
数最多的数据即为所求;
(2)根据(1)中的数据画图即可;
(3)先算出样本中学习时长在5<x≤7小时的人数所占的百分比,再用总数乘以这个百分
比即可.
【解答】解:(1)由总人数是20人可得在5<x≤6的人数是20﹣2﹣8﹣4=6(人),所以a
=6,
根据数据显示,6.5出现的次数最多,所以这组数据的众数b=6.5;
故答案为:6,6.5;
(2)由(1)得a=6.
频数分布直方图补充如下:
第17页(共26页)(3)由图可知,学习时长在5<x≤7小时的人数所占的百分比= ×100%=70%,
∴1000×70%=700(人).
∴学习时长在5<x≤7小时的人数是700人.
【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获
取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.也考查了
众数,利用样本估计总体.
22.(6分)如图,在△ABC中,AB=AC,以AB为直径的 O交BC于点D,过点D作
DE⊥AC,垂足为点E. ⊙
(1)求证:△ABD≌△ACD;
(2)判断直线DE与 O的位置关系,并说明理由.
⊙
【分析】(1)AB为 O的直径得AD⊥BC,结合AB=AC,用HL证明三角形全等;
(2)由△ABD≌△AC⊙D得BD=BC,结合AO=BO得OD为△ABC的中位线,由DE⊥AC
得OD⊥DE,可得直线DE为 O切线.
【解答】(1)证明:∵AB为⊙O的直径,
∴AD⊥BC, ⊙
在Rt△ADB和Rt△ADC中 ,
∴Rt△ABD≌Rt△ACD(HL);
(2)直线DE与 O相切,理由如下:
连接OD,如图所⊙示:
由△ABD≌△ACD知:BD=DC,
又∵OA=OB,
第18页(共26页)∴OD为△ABC的中位线,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∵OD为 O的半径,
∴DE与⊙O相切.
【点评】本⊙题考查了直线与圆的位置关系,全等三角形判定和性质,切线的判定,平行线的
判定和性质,熟知以上知识的应用是解题的关键.
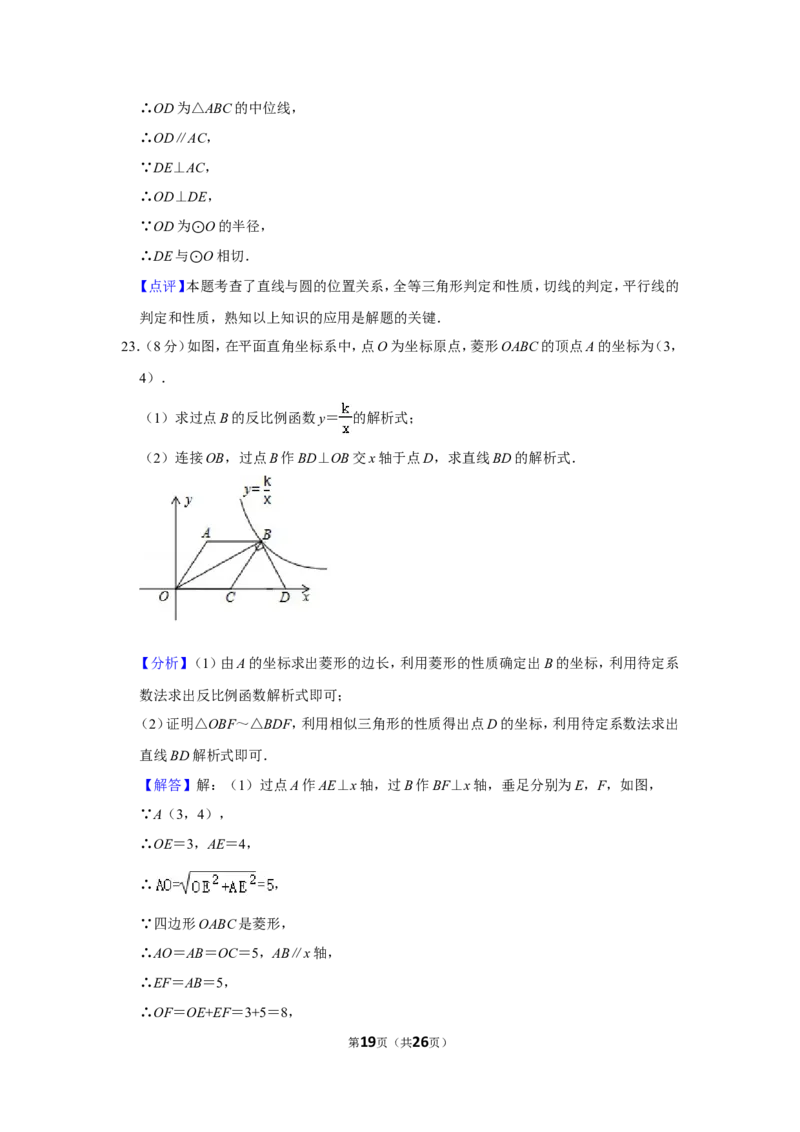
23.(8分)如图,在平面直角坐标系中,点O为坐标原点,菱形OABC的顶点A的坐标为(3,
4).
(1)求过点B的反比例函数y= 的解析式;
(2)连接OB,过点B作BD⊥OB交x轴于点D,求直线BD的解析式.
【分析】(1)由A的坐标求出菱形的边长,利用菱形的性质确定出B的坐标,利用待定系
数法求出反比例函数解析式即可;
(2)证明△OBF~△BDF,利用相似三角形的性质得出点D的坐标,利用待定系数法求出
直线BD解析式即可.
【解答】解:(1)过点A作AE⊥x轴,过B作BF⊥x轴,垂足分别为E,F,如图,
∵A(3,4),
∴OE=3,AE=4,
∴ ,
∵四边形OABC是菱形,
∴AO=AB=OC=5,AB∥x轴,
∴EF=AB=5,
∴OF=OE+EF=3+5=8,
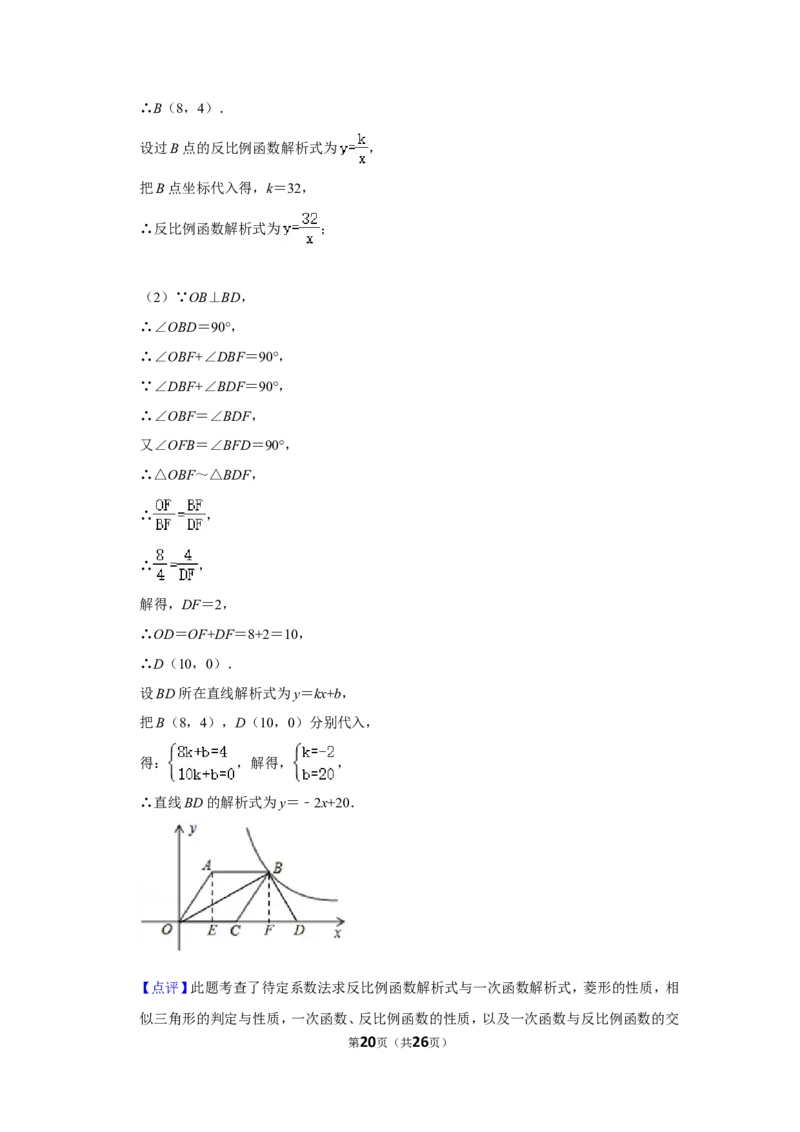
第19页(共26页)∴B(8,4).
设过B点的反比例函数解析式为 ,
把B点坐标代入得,k=32,
∴反比例函数解析式为 ;
(2)∵OB⊥BD,
∴∠OBD=90°,
∴∠OBF+∠DBF=90°,
∵∠DBF+∠BDF=90°,
∴∠OBF=∠BDF,
又∠OFB=∠BFD=90°,
∴△OBF~△BDF,
∴ ,
∴ ,
解得,DF=2,
∴OD=OF+DF=8+2=10,
∴D(10,0).
设BD所在直线解析式为y=kx+b,
把B(8,4),D(10,0)分别代入,
得: ,解得, ,
∴直线BD的解析式为y=﹣2x+20.
【点评】此题考查了待定系数法求反比例函数解析式与一次函数解析式,菱形的性质,相
似三角形的判定与性质,一次函数、反比例函数的性质,以及一次函数与反比例函数的交
第20页(共26页)点,熟练掌握待定系数法是解本题的关键.
24.(8分)习近平总书记说:“读书可以让人保持思想活力,让人得到智慧启发,让人滋养浩
然之气”.某校为提高学生的阅读品味,现决定购买获得第十届茅盾文学奖的《北上》(徐
则臣著)和《牵风记》(徐怀中著)两种书共50本.已知购买2本《北上》和1本《牵风记》需
100元;购买6本《北上》与购买7本《牵风记》的价格相同.
(1)求这两种书的单价;
(2)若购买《北上》的数量不少于所购买《牵风记》数量的一半,且购买两种书的总价不超
过1600元.请问有哪几种购买方案?哪种购买方案的费用最低?最低费用为多少元?
【分析】(1)设购买《北上》的单价为x元,《牵风记》的单价为y元,根据“购买2本《北
上》和1本《牵风记》需100元”和“购买6本《北上》与购买7本《牵风记》的价格相同”
建立方程组求解即可;
(2)设购买《北上》的数量n本,则购买《牵风记》的数量为(50﹣n)本,根据“购买《北上》
的数量不少于所购买《牵风记》数量的一半”和“购买两种书的总价不超过1600元”两
个不等关系列不等式组解答并确定整数解即可.
【解答】解:(1)设购买《北上》的单价为x元,《牵风记》的单价为y元,
由题意得: ,
解得 .
答:购买《北上》的单价为35元,《牵风记》的单价为30元;
(2)设购买《北上》的数量n本,则购买《牵风记》的数量为(50﹣n)本,
根据题意得 ,
解得: ,
则n可以取17、18、19、20,
当n=17时,50﹣n=33,共花费17×35+33×30=1585(元);
当n=18时,50﹣n=32,共花费18×35+32×30=1590(元);
当n=19时,50﹣n=31,共花费19×35+31×30=1595(元);
当n=20时,50﹣n=30,共花费20×35+30×30=1600(元);
所以,共有4种购买方案分别为:购买《北上》和《牵风记》的数量分别为17本和33本,购
第21页(共26页)买《北上》和《牵风记》的数量分别为18本和32本,购买《北上》和《牵风记》的数量分别为
19本和31本,购买《北上》和《牵风记》的数量分别为20本和30本;其中购买《北上》和
《牵风记》的数量分别为17本和33本费用最低,最低费用为1585元.
【点评】本题考查了二元一次方程组和不等式组的应用,弄清题意、确定等量关系和不等
关系是解答本题的关键.
25.(10分)阅读材料:三角形的三条中线必交于一点,这个交点称为三角形的重心.
(1)特例感知:如图(一),已知边长为2的等边△ABC的重心为点O,求△OBC与△ABC
的面积.
(2)性质探究:如图(二),已知△ABC的重心为点O,请判断 、 是否都为定值?
如果是,分别求出这两个定值;如果不是,请说明理由.
(3)性质应用:如图(三),在正方形ABCD中,点E是CD的中点,连接BE交对角线AC
于点M.
若正方形ABCD的边长为4,求EM的长度;
①若S△CME =1,求正方形ABCD的面积.
②
【分析】(1)连接DE,利用相似三角形证明 ,运用勾股定理求出AD的长,运用三
角形面积公式求解即可;
(2)根据(1)的证明可求解;
(3) 证明△CME∽△ABM,得 ,再运用勾股定理求出BE的长即可解决问题;
①
分别求出S△BMC 和S△ABM 即可求得正方形ABCD的面积.
②【解答】解:(1)连接DE,如图一,
∵点O是△ABC的重心,
∴AD,BE是BC,AC边上的中线,
第22页(共26页)∴D,E为BC,AC边上的中点,
∴DE为△ABC的中位线,
∴DE∥AB,DE= AB,
∴△ODE∽△OAB,
∴ = ,
∵AB=2,BD=1,∠ADB=90°,
∴AD= ,OD= ,
∴ , = ;
(2)由(1)同理可得, ,是定值;
点O到BC的距离和点A到BC的距离之比为1:3,
则△OBC和△ABC的面积之比等于点O到BC的距离和点A到BC的距离之比,
故 = ,是定值;
(3) ∵四边形ABCD是正方形,
∴CD∥①AB,AB=BC=CD=4,
∴△CME~△AMB,
∴ ,
∵E为CD的中点,
∴ ,
∴ ,
∴ ,
∴ ,
即 ;
第23页(共26页)∴S△CME =1,且 ,
②
∴S△BMC =2,
∵ ,
∴ ,
∴S△AMB =4,
∴S△ABC =S△BMC +S△ABM =2+4=6,
又S△ADC =S△ABC ,
∴S△ADC =6,
∴正方形ABCD的面积为:6+6=12.
【点评】本题是一道相似形综合题目,主要考查的是三角形重心的性质、全等三角形的判
定与性质、勾股定理及相似三角形的判定与性质,解答此题的关键是明确题意,找出所求
问题需要的条件,利用数形结合的思想解答.
26.(10分)如图,抛物线y=﹣x2+bx+5与x轴交于A,B两点.
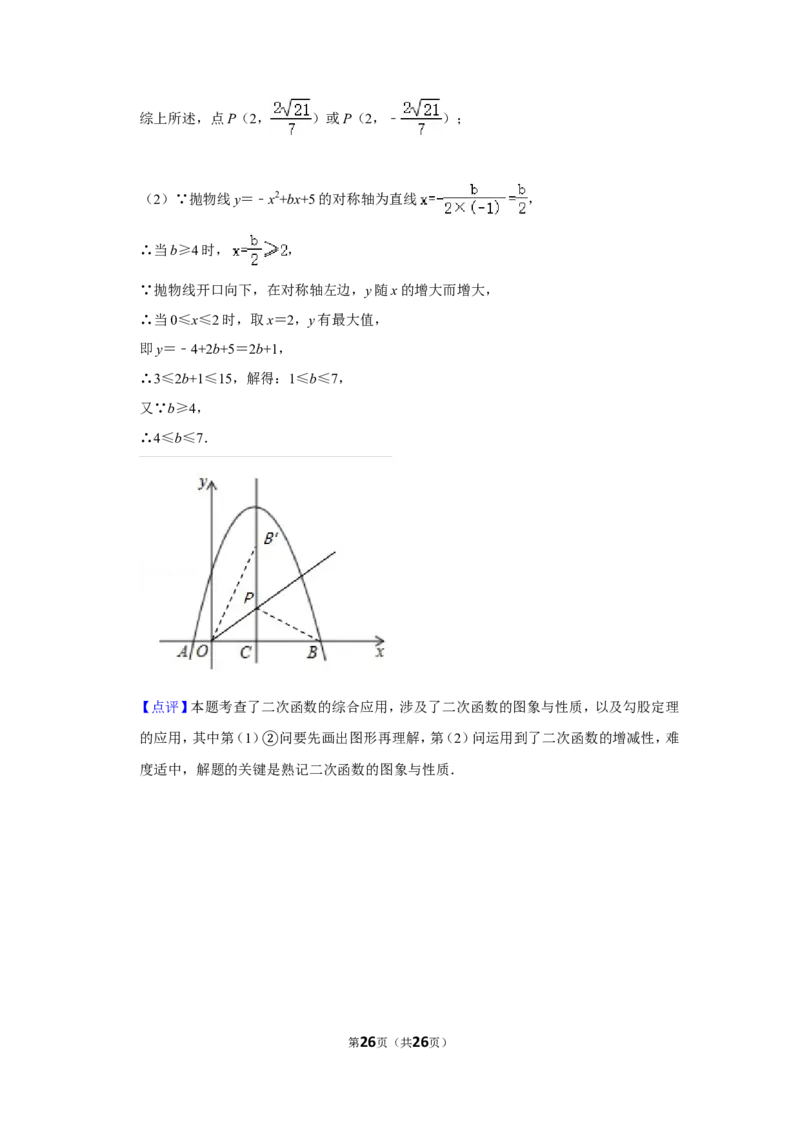
(1)若过点C的直线x=2是抛物线的对称轴.
求抛物线的解析式;
①对称轴上是否存在一点P,使点B关于直线OP的对称点B'恰好落在对称轴上.若存在,
第24页(共26页)
②请求出点P的坐标;若不存在,请说明理由.
(2)当b≥4,0≤x≤2时,函数值y的最大值满足3≤y≤15,求b的取值范围.
【分析】(1) 根据抛物线的对称轴公式即可求出解析式;
如图,若点P①在x轴上方,点B关于OP对称的点B'在对称轴上,连接OB′、PB,根据
②轴对称的性质得到 OB'=OB,PB'=PB,求出点 B 的坐标,利用勾股定理得到
,再根据PB'=PB,列出方程解答,同理得到点P在x轴下方时的坐标即
可;
(2)当b≥4时,确定对称轴的位置,再结合开口方向,确定当0≤x≤2时,函数的增减性,
从而得到当x=2时,函数取最大值,再列出不等式解答即可.
【解答】解:(1) 抛物线y=﹣x2+bx+5的对称轴为直线 ,
①
∴若过点C的直线x=2是抛物线的对称轴,
则 ,解得:b=4,
∴抛物线的解析式为y=﹣x2+4x+5;
存在,
②如图,若点P在x轴上方,点B关于OP对称的点B'在对称轴上,连接OB′、PB,
则OB'=OB,PB'=PB,
对于y=﹣x2+4x+5,令y=0,则﹣x2+4x+5=0,
解得:x =﹣1,x =5,
1 2
∴A(﹣1,0),B(5,0),
∴OB'=OB=5,
∴ ,
∴ ,
设点P(2,m),
由PB'=PB可得: ,解得: ,
∴P(2, );
同理,当点P在x轴下方时,P(2,﹣ ).
第25页(共26页)综上所述,点P(2, )或P(2,﹣ );
(2)∵抛物线y=﹣x2+bx+5的对称轴为直线 ,
∴当b≥4时, ,
∵抛物线开口向下,在对称轴左边,y随x的增大而增大,
∴当0≤x≤2时,取x=2,y有最大值,
即y=﹣4+2b+5=2b+1,
∴3≤2b+1≤15,解得:1≤b≤7,
又∵b≥4,
∴4≤b≤7.
【点评】本题考查了二次函数的综合应用,涉及了二次函数的图象与性质,以及勾股定理
的应用,其中第(1) 问要先画出图形再理解,第(2)问运用到了二次函数的增减性,难
度适中,解题的关键②是熟记二次函数的图象与性质.
第26页(共26页)