文档内容
2020年湖南省湘西州中考数学试卷
一、选择题(本大题共10小题,每小题4分,共40分.请将每个小题所给四个选项中唯一正
确选项的代号填涂在答题卡相应的位置上)
1.(4分)下列各数中,比﹣2小的数是( )
A.0 B.﹣1 C.﹣3 D.3
2.(4分)2019年中国与“一带一路”沿线国家货物贸易进出口总额达到92700亿元,用科
学记数法表示92700是( )
A.0.927×105 B.9.27×104 C.92.7×103 D.927×102
3.(4分)下列运算正确的是( )
A. =﹣2 B.(x﹣y)2=x2﹣y2
C. + = D.(﹣3a)2=9a2
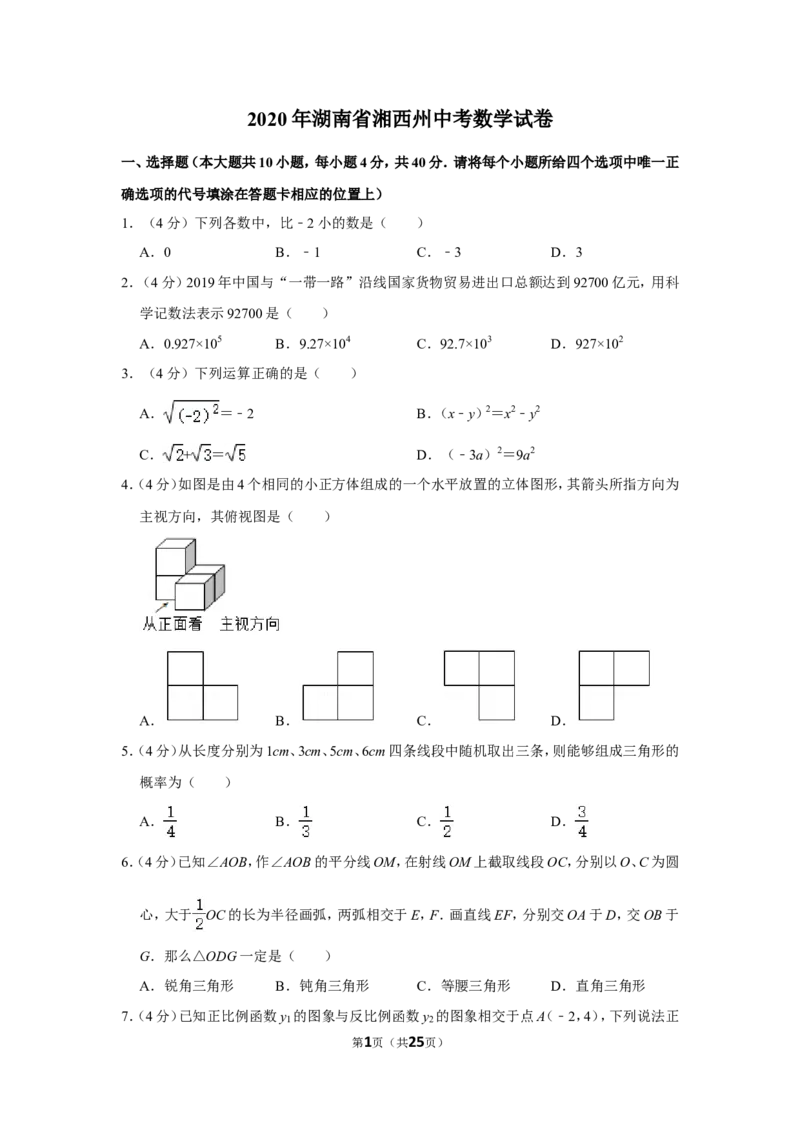
4.(4分)如图是由4个相同的小正方体组成的一个水平放置的立体图形,其箭头所指方向为
主视方向,其俯视图是( )
A. B. C. D.
5.(4分)从长度分别为1cm、3cm、5cm、6cm四条线段中随机取出三条,则能够组成三角形的
概率为( )
A. B. C. D.
6.(4分)已知∠AOB,作∠AOB的平分线OM,在射线OM上截取线段OC,分别以O、C为圆
心,大于 OC的长为半径画弧,两弧相交于E,F.画直线EF,分别交OA于D,交OB于
G.那么△ODG一定是( )
A.锐角三角形 B.钝角三角形 C.等腰三角形 D.直角三角形
7.(4分)已知正比例函数y 的图象与反比例函数y 的图象相交于点A(﹣2,4),下列说法正
1 2
第1页(共25页)确的是( )
A.正比例函数y 的解析式是y =2x
1 1
B.两个函数图象的另一交点坐标为(4,﹣2)
C.正比例函数y 与反比例函数y 都随x的增大而增大
1 2
D.当x<﹣2或0<x<2时,y <y
2 1
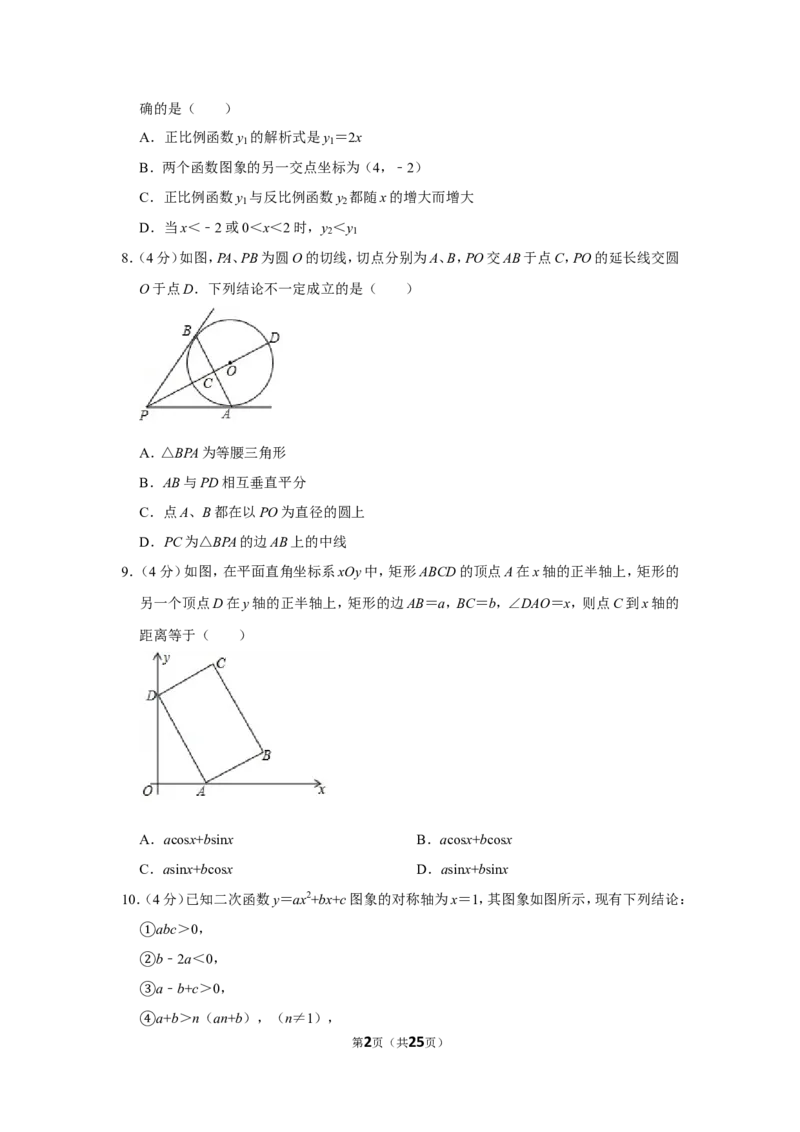
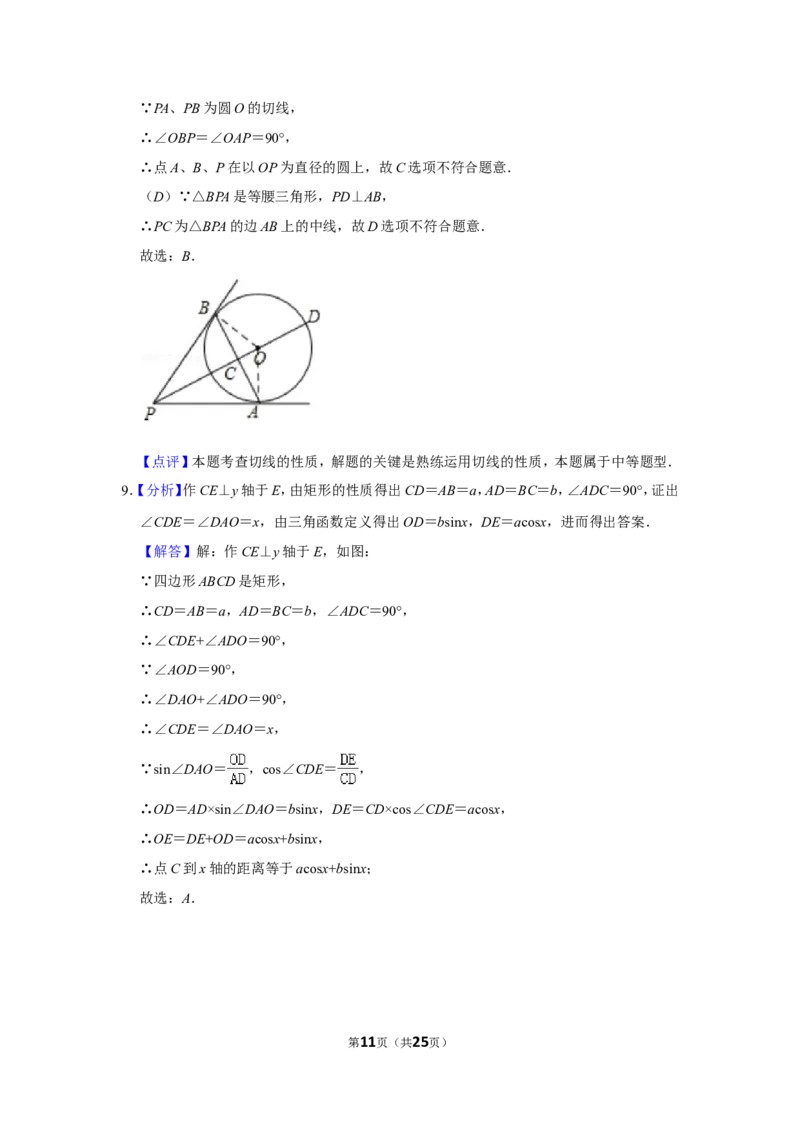
8.(4分)如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆
O于点D.下列结论不一定成立的是( )
A.△BPA为等腰三角形
B.AB与PD相互垂直平分
C.点A、B都在以PO为直径的圆上
D.PC为△BPA的边AB上的中线
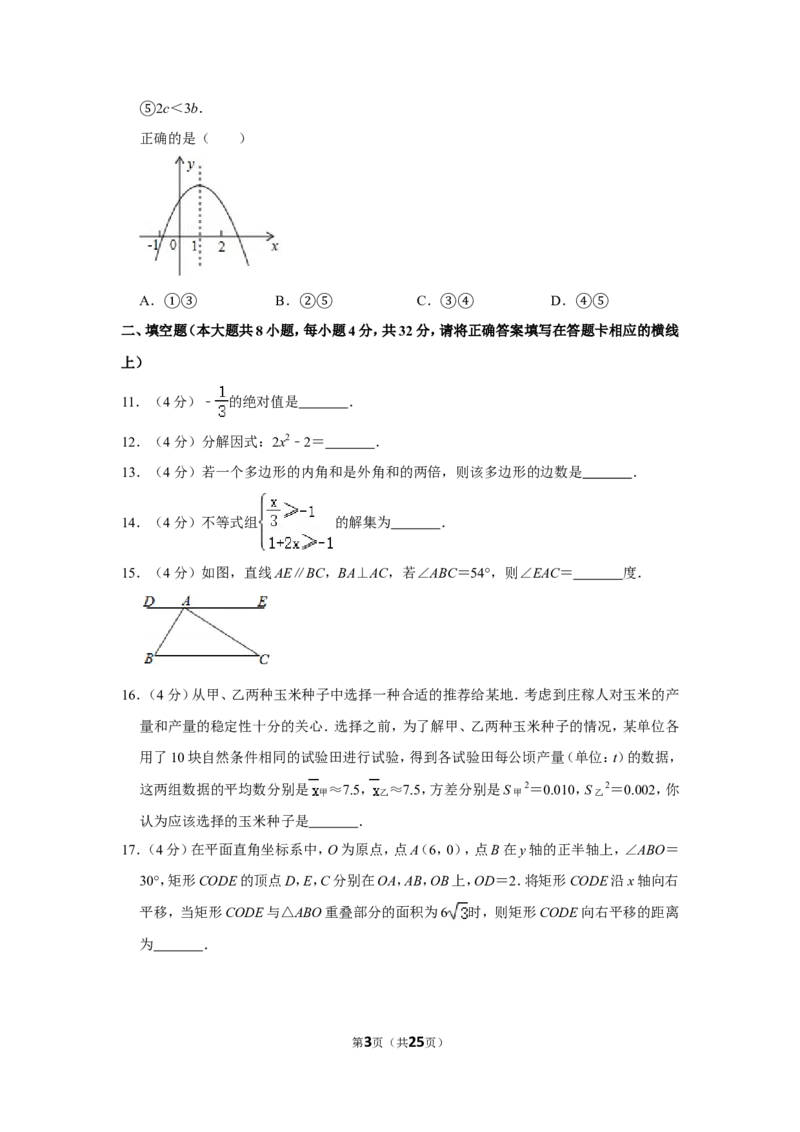
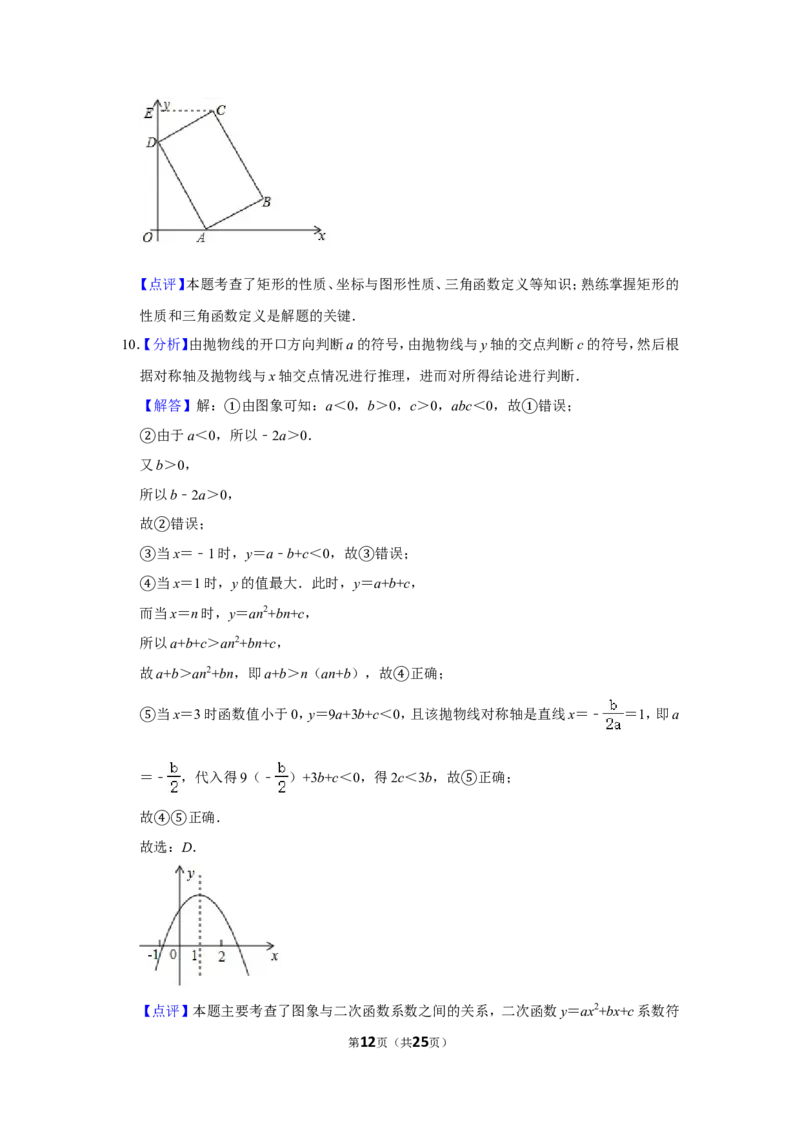
9.(4分)如图,在平面直角坐标系xOy中,矩形ABCD的顶点A在x轴的正半轴上,矩形的
另一个顶点D在y轴的正半轴上,矩形的边AB=a,BC=b,∠DAO=x,则点C到x轴的
距离等于( )
A.acosx+bsinx B.acosx+bcosx
C.asinx+bcosx D.asinx+bsinx
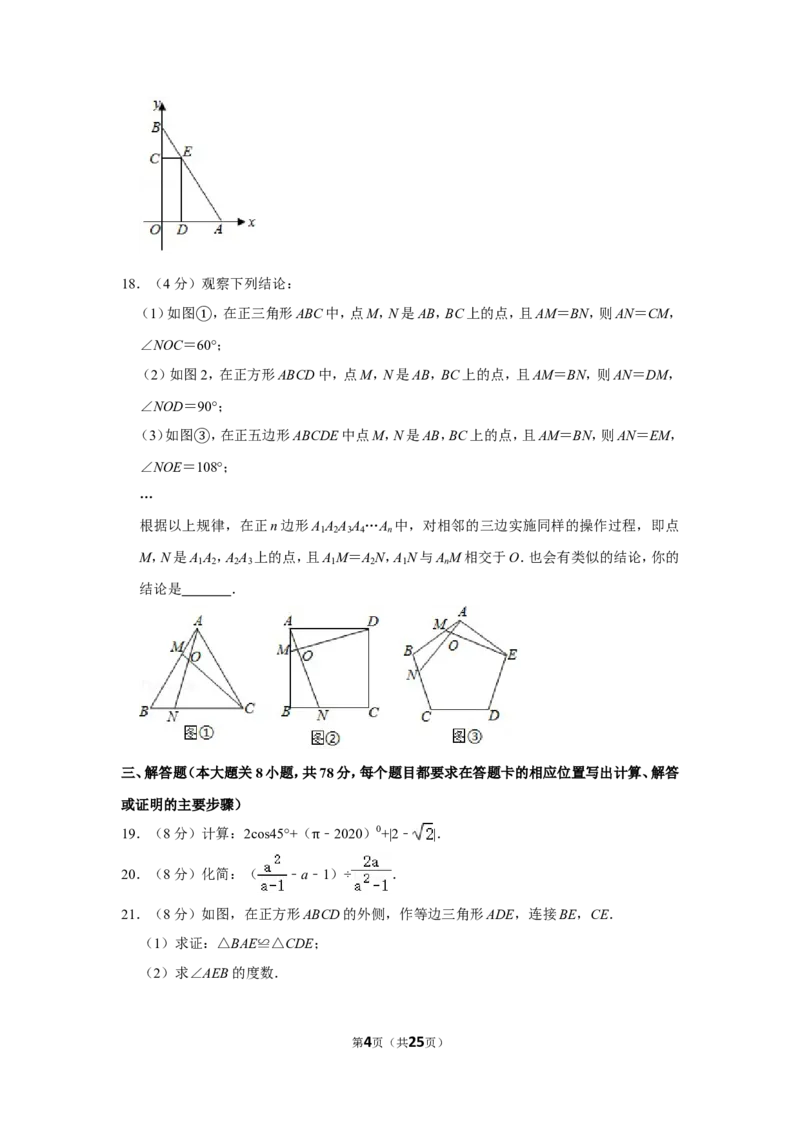
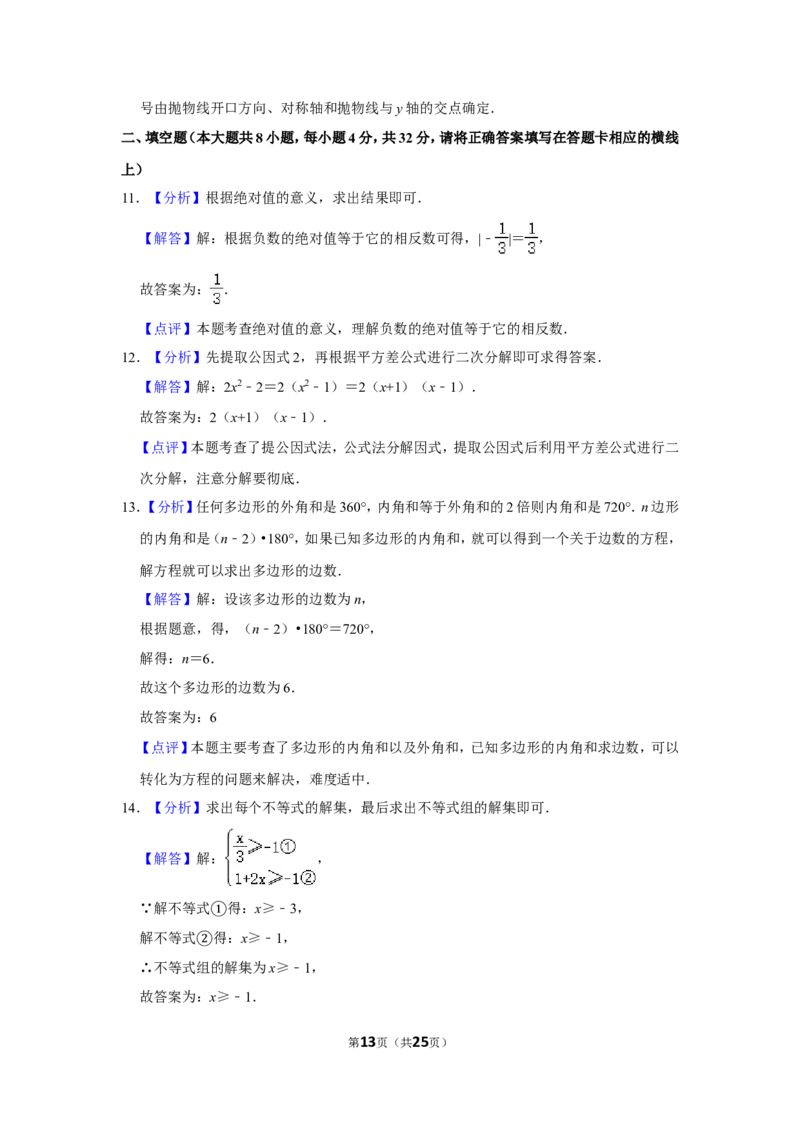
10.(4分)已知二次函数y=ax2+bx+c图象的对称轴为x=1,其图象如图所示,现有下列结论:
abc>0,
①b﹣2a<0,
②a﹣b+c>0,
③a+b>n(an+b),(n≠1),
第2页(共25页)
④2c<3b.
⑤正确的是( )
A. B. C. D.
二、填空①题③(本大题共8小题,②每⑤小题4分,共32分,请③将④正确答案填写在答④题⑤卡相应的横线
上)
11.(4分)﹣ 的绝对值是 .
12.(4分)分解因式:2x2﹣2= .
13.(4分)若一个多边形的内角和是外角和的两倍,则该多边形的边数是 .
14.(4分)不等式组 的解集为 .
15.(4分)如图,直线AE∥BC,BA⊥AC,若∠ABC=54°,则∠EAC= 度.
16.(4分)从甲、乙两种玉米种子中选择一种合适的推荐给某地.考虑到庄稼人对玉米的产
量和产量的稳定性十分的关心.选择之前,为了解甲、乙两种玉米种子的情况,某单位各
用了10块自然条件相同的试验田进行试验,得到各试验田每公顷产量(单位:t)的数据,
这两组数据的平均数分别是
甲
≈7.5,
乙
≈7.5,方差分别是S甲 2=0.010,S乙 2=0.002,你
认为应该选择的玉米种子是 .
17.(4分)在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=
30°,矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.将矩形CODE沿x轴向右
平移,当矩形CODE与△ABO重叠部分的面积为6 时,则矩形CODE向右平移的距离
为 .
第3页(共25页)18.(4分)观察下列结论:
(1)如图 ,在正三角形ABC中,点M,N是AB,BC上的点,且AM=BN,则AN=CM,
∠NOC=①60°;
(2)如图2,在正方形ABCD中,点M,N是AB,BC上的点,且AM=BN,则AN=DM,
∠NOD=90°;
(3)如图 ,在正五边形ABCDE中点M,N是AB,BC上的点,且AM=BN,则AN=EM,
∠NOE=③108°;
…
根据以上规律,在正n边形A A A A …A 中,对相邻的三边实施同样的操作过程,即点
1 2 3 4 n
M,N是A A ,A A 上的点,且A M=A N,A N与A M相交于O.也会有类似的结论,你的
1 2 2 3 1 2 1 n
结论是 .
三、解答题(本大題关8小题,共78分,每个题目都要求在答题卡的相应位置写出计算、解答
或证明的主要步骤)
19.(8分)计算:2cos45°+( ﹣2020)0+|2﹣ |.
π
20.(8分)化简:( ﹣a﹣1)÷ .
21.(8分)如图,在正方形ABCD的外侧,作等边三角形ADE,连接BE,CE.
(1)求证:△BAE≌△CDE;
(2)求∠AEB的度数.
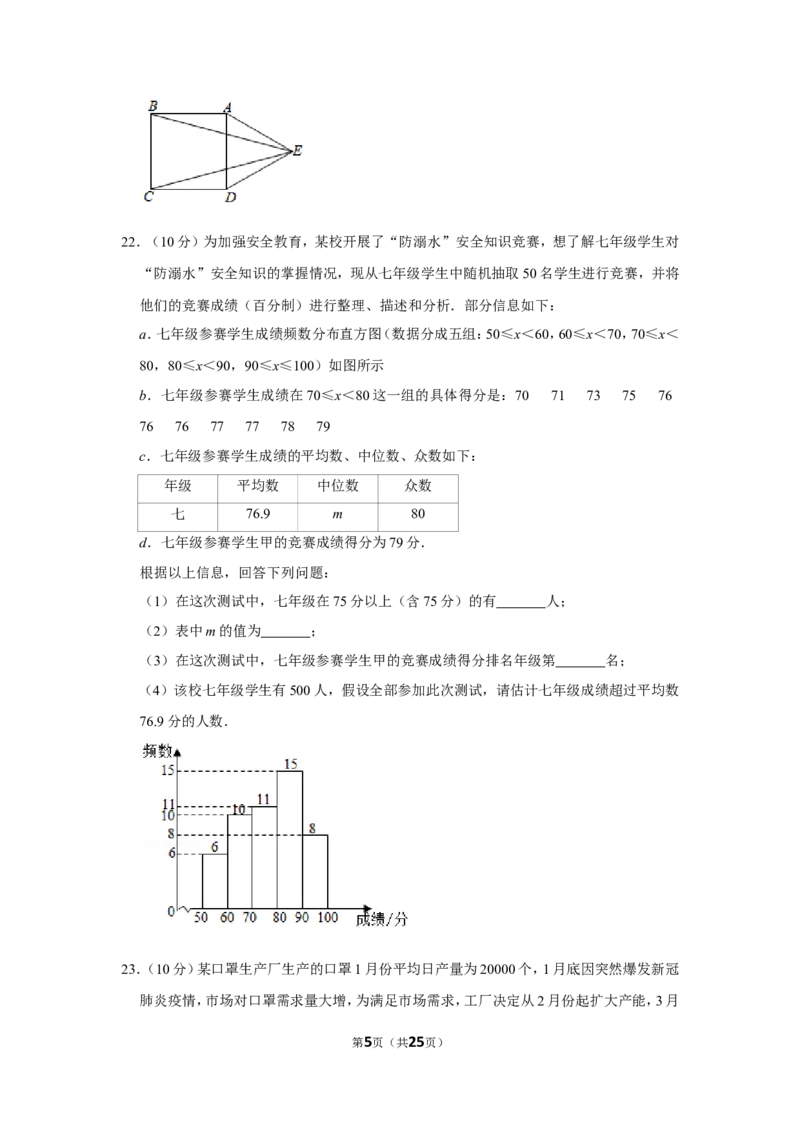
第4页(共25页)22.(10分)为加强安全教育,某校开展了“防溺水”安全知识竞赛,想了解七年级学生对
“防溺水”安全知识的掌握情况,现从七年级学生中随机抽取50名学生进行竞赛,并将
他们的竞赛成绩(百分制)进行整理、描述和分析.部分信息如下:
a.七年级参赛学生成绩频数分布直方图(数据分成五组:50≤x<60,60≤x<70,70≤x<
80,80≤x<90,90≤x≤100)如图所示
b.七年级参赛学生成绩在70≤x<80这一组的具体得分是:70 71 73 75 76
76 76 77 77 78 79
c.七年级参赛学生成绩的平均数、中位数、众数如下:
年级 平均数 中位数 众数
七 76.9 m 80
d.七年级参赛学生甲的竞赛成绩得分为79分.
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在75分以上(含75分)的有 人;
(2)表中m的值为 ;
(3)在这次测试中,七年级参赛学生甲的竞赛成绩得分排名年级第 名;
(4)该校七年级学生有500人,假设全部参加此次测试,请估计七年级成绩超过平均数
76.9分的人数.
23.(10分)某口罩生产厂生产的口罩1月份平均日产量为20000个,1月底因突然爆发新冠
肺炎疫情,市场对口罩需求量大增,为满足市场需求,工厂决定从2月份起扩大产能,3月
第5页(共25页)份平均日产量达到24200个.
(1)求口罩日产量的月平均增长率;
(2)按照这个增长率,预计4月份平均日产量为多少?
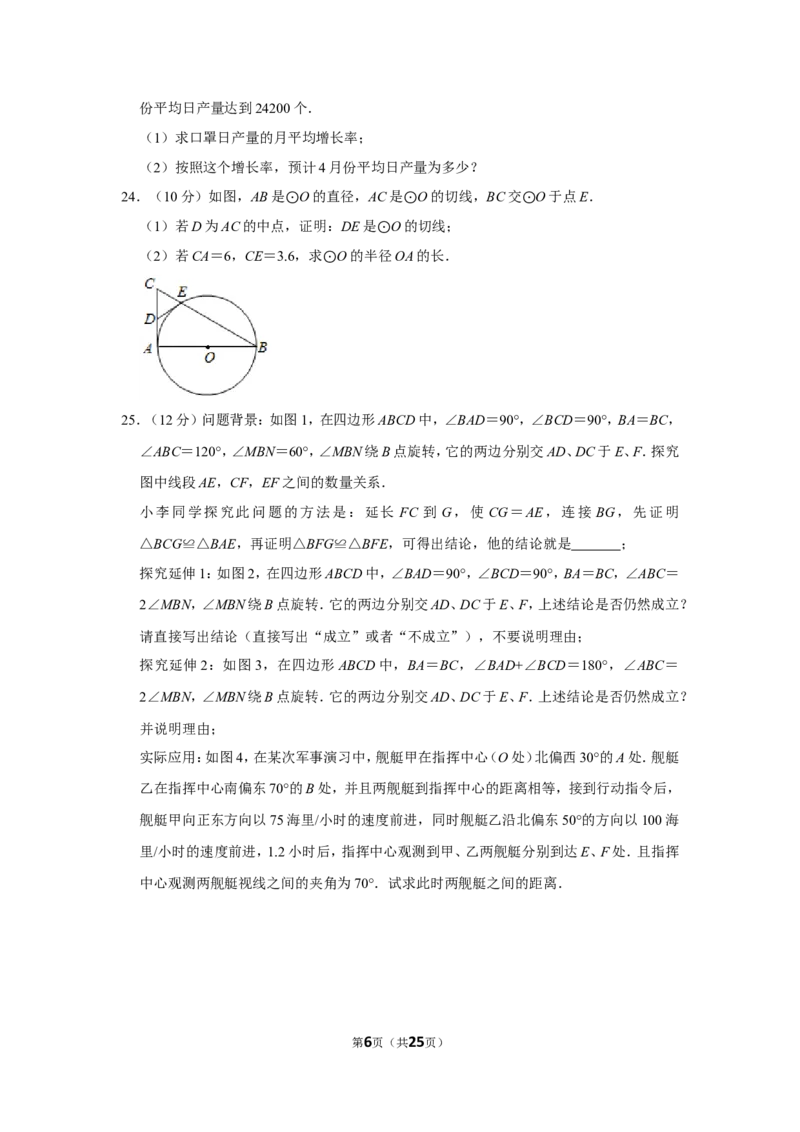
24.(10分)如图,AB是 O的直径,AC是 O的切线,BC交 O于点E.
(1)若D为AC的中点,⊙证明:DE是 O⊙的切线; ⊙
(2)若CA=6,CE=3.6,求 O的半⊙径OA的长.
⊙
25.(12分)问题背景:如图1,在四边形ABCD中,∠BAD=90°,∠BCD=90°,BA=BC,
∠ABC=120°,∠MBN=60°,∠MBN绕B点旋转,它的两边分别交AD、DC于E、F.探究
图中线段AE,CF,EF之间的数量关系.
小李同学探究此问题的方法是:延长 FC 到 G,使 CG=AE,连接 BG,先证明
△BCG≌△BAE,再证明△BFG≌△BFE,可得出结论,他的结论就是 ;
探究延伸1:如图2,在四边形ABCD中,∠BAD=90°,∠BCD=90°,BA=BC,∠ABC=
2∠MBN,∠MBN绕B点旋转.它的两边分别交AD、DC于E、F,上述结论是否仍然成立?
请直接写出结论(直接写出“成立”或者“不成立”),不要说明理由;
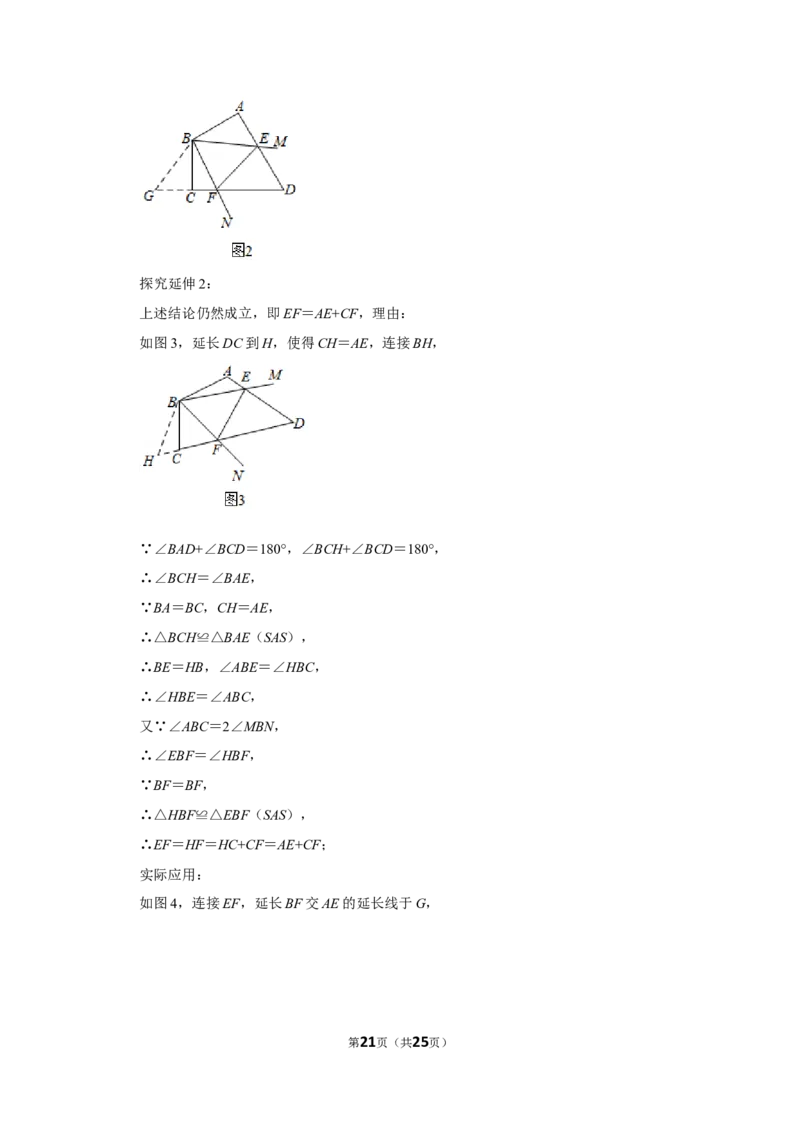
探究延伸2:如图3,在四边形ABCD中,BA=BC,∠BAD+∠BCD=180°,∠ABC=
2∠MBN,∠MBN绕B点旋转.它的两边分别交AD、DC于E、F.上述结论是否仍然成立?
并说明理由;
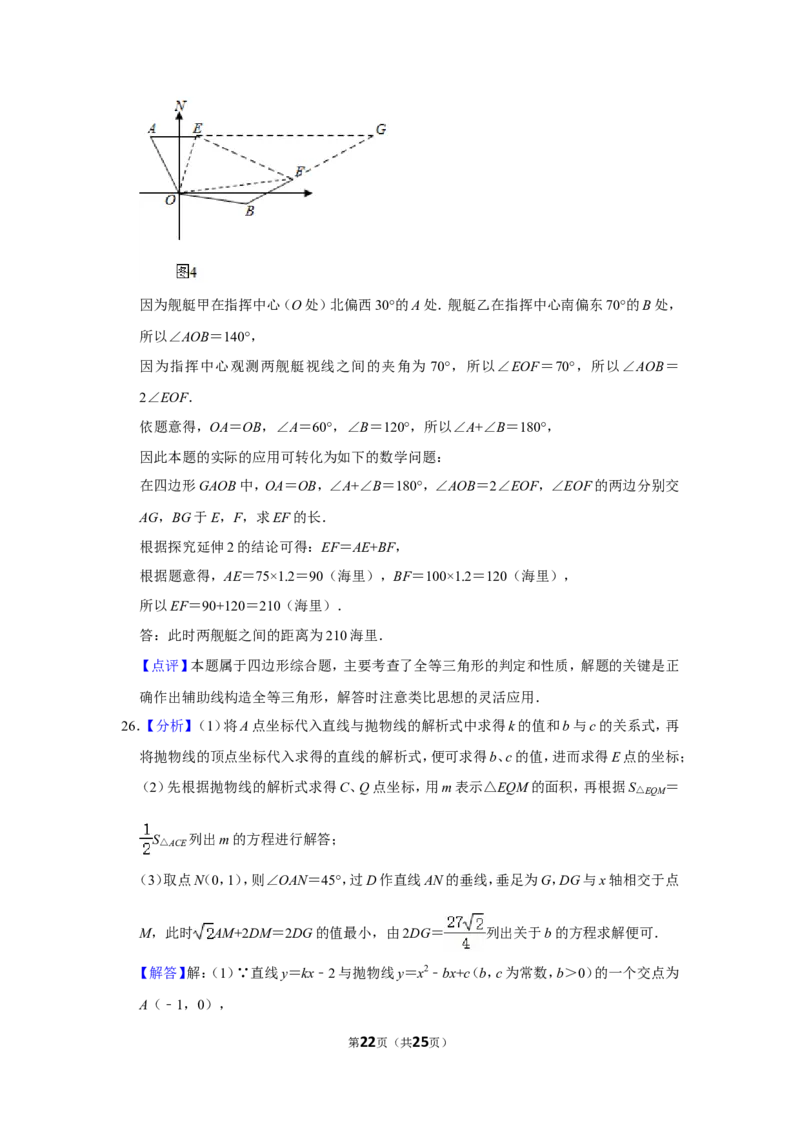
实际应用:如图4,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处.舰艇
乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,
舰艇甲向正东方向以75海里/小时的速度前进,同时舰艇乙沿北偏东50°的方向以100海
里/小时的速度前进,1.2小时后,指挥中心观测到甲、乙两舰艇分别到达E、F处.且指挥
中心观测两舰艇视线之间的夹角为70°.试求此时两舰艇之间的距离.
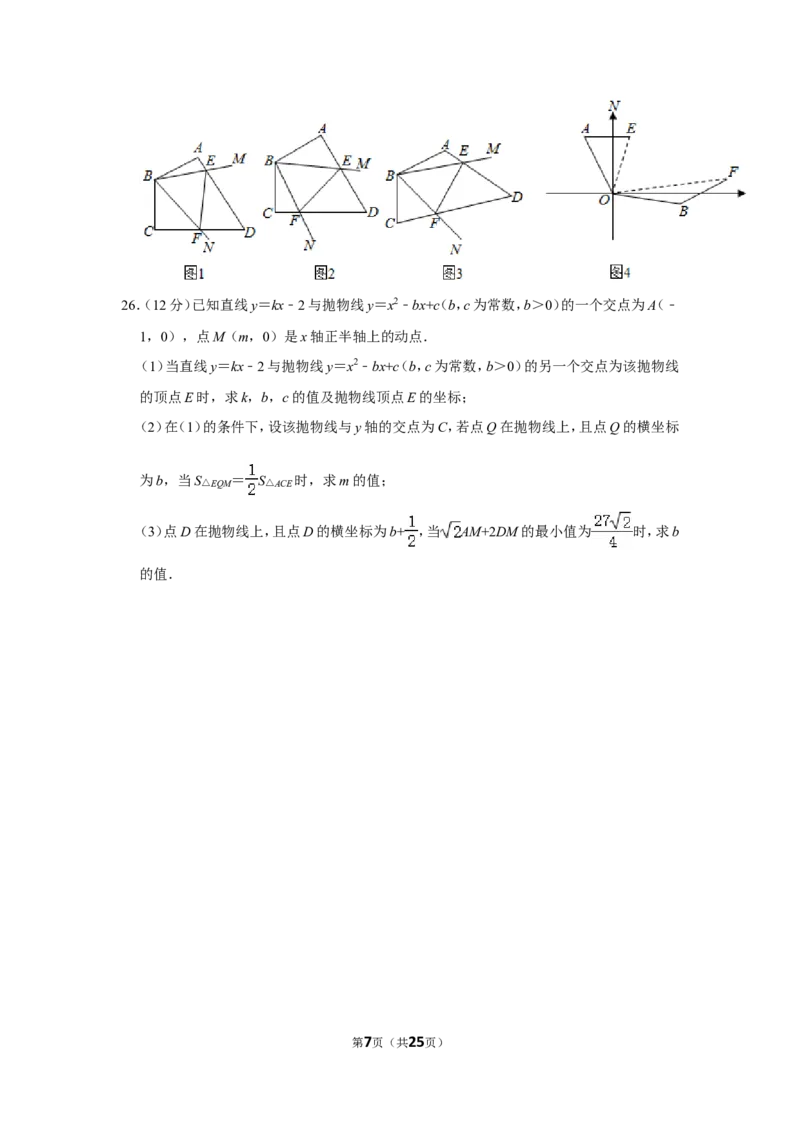
第6页(共25页)26.(12分)已知直线y=kx﹣2与抛物线y=x2﹣bx+c(b,c为常数,b>0)的一个交点为A(﹣
1,0),点M(m,0)是x轴正半轴上的动点.
(1)当直线y=kx﹣2与抛物线y=x2﹣bx+c(b,c为常数,b>0)的另一个交点为该抛物线
的顶点E时,求k,b,c的值及抛物线顶点E的坐标;
(2)在(1)的条件下,设该抛物线与y轴的交点为C,若点Q在抛物线上,且点Q的横坐标
为b,当S△EQM = S△ACE 时,求m的值;
(3)点D在抛物线上,且点D的横坐标为b+ ,当 AM+2DM的最小值为 时,求b
的值.
第7页(共25页)2020年湖南省湘西州中考数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,共40分.请将每个小题所给四个选项中唯一正
确选项的代号填涂在答题卡相应的位置上)
1.【分析】利用数轴表示这些数,从而比较大小.
【解答】解:将这些数在数轴上表示出来:
∴﹣3<﹣2<﹣1<0<3,
∴比﹣2小的数是﹣3,
故选:C.
【点评】考查了有理数大小比较法则.正数大于0,0大于负数,正数大于负数;两个负数,
绝对值大的反而小.
2.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为正整数.
【解答】解:92700=9.27×104.
故选:B.
【点评】此题考查科学记数法表示较大的数的方法,把一个大于10的数记成a×10n的形式,
其中1≤|a|<10,n是正整数,这种记数法叫做科学记数法.
3.【分析】根据二次根式的加减法、幂的乘方与积的乘方、完全平方公式、二次根式的性质与
化简,进行计算即可判断.
【解答】解:A. =2,所以A选项错误;
B.(x﹣y)2=x2﹣2xy+y2,所以B选项错误;
C. + ≠ ,所以C选项错误;
D.(﹣3a)2=9a2.所以D选项正确.
故选:D.
【点评】本题考查了二次根式的加减法、幂的乘方与积的乘方、完全平方公式、二次根式的
性质与化简,解决本题的关键是综合运用以上知识.
4.【分析】根据从上边看得到的图形是俯视图,可得答案.
【解答】解:从上边看有两层,底层右边是一个小正方形,上层是两个小正方形,
第8页(共25页)故选:C.
【点评】本题考查了简单组合体的三视图,从上边看得到的图形是俯视图.
5.【分析】列举出所有可能出现的结果情况,进而求出能构成三角形的概率.
【解答】解:从长度为1cm、3cm、5cm、6cm四条线段中随机取出三条,
共有以下4种结果(不分先后):
1cm、3cm、5cm,
1cm、3cm、6cm,
3cm、5cm、6cm,
1cm、5cm、6cm,
其中,能构成三角形的只有1种,
∴P(构成三角形) = .
故选:A.
【点评】本题考查随机事件发生的概率,列举出所有可能出现的结果情况,是正确解答的
关键.
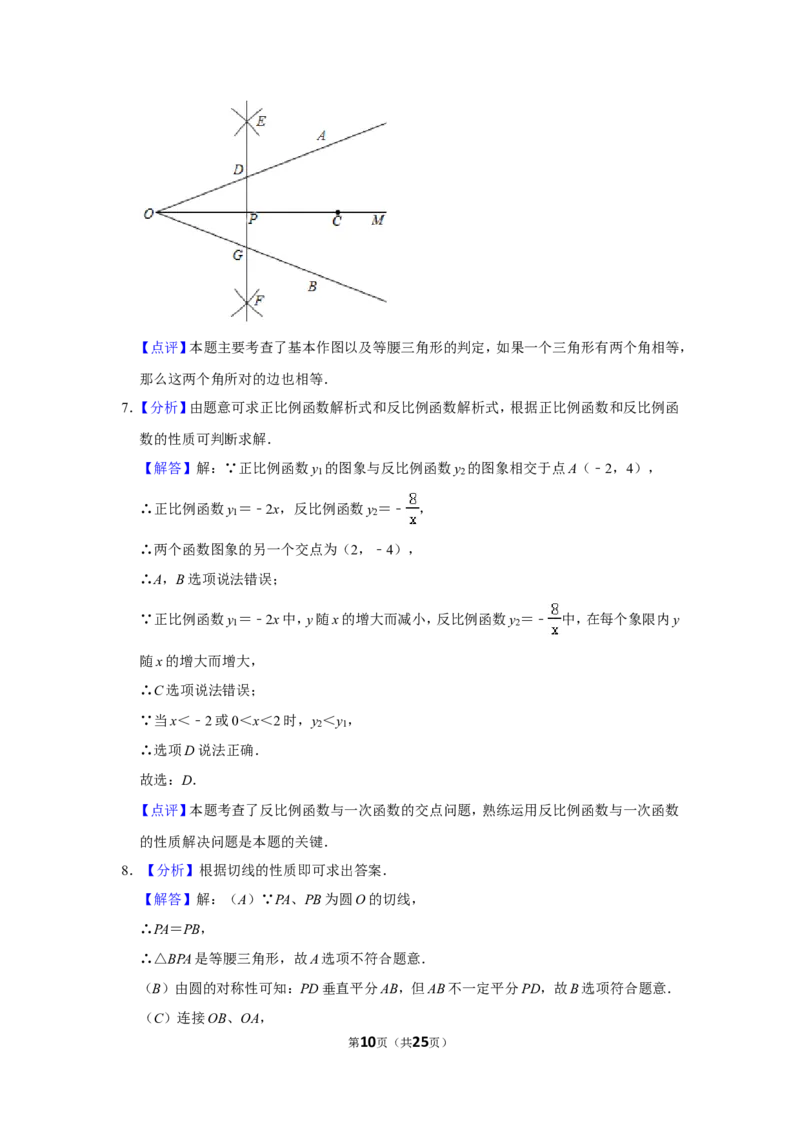
6.【分析】依据已知条件即可得到∠ODP=∠OGP,即可得到OD=OG,进而得出△ODG是
等腰三角形.
【解答】解:如图所示,∵OM平分∠AOB,
∴∠AOC=∠BOC,
由题意可得,DG垂直平分OC,
∴∠OPD=∠OPG=90°,
∴∠ODP=∠OGP,
∴OD=OG,
∴△ODG是等腰三角形,
故选:C.
第9页(共25页)【点评】本题主要考查了基本作图以及等腰三角形的判定,如果一个三角形有两个角相等,
那么这两个角所对的边也相等.
7.【分析】由题意可求正比例函数解析式和反比例函数解析式,根据正比例函数和反比例函
数的性质可判断求解.
【解答】解:∵正比例函数y 的图象与反比例函数y 的图象相交于点A(﹣2,4),
1 2
∴正比例函数y =﹣2x,反比例函数y =﹣ ,
1 2
∴两个函数图象的另一个交点为(2,﹣4),
∴A,B选项说法错误;
∵正比例函数y =﹣2x中,y随x的增大而减小,反比例函数y =﹣ 中,在每个象限内y
1 2
随x的增大而增大,
∴C选项说法错误;
∵当x<﹣2或0<x<2时,y <y ,
2 1
∴选项D说法正确.
故选:D.
【点评】本题考查了反比例函数与一次函数的交点问题,熟练运用反比例函数与一次函数
的性质解决问题是本题的关键.
8.【分析】根据切线的性质即可求出答案.
【解答】解:(A)∵PA、PB为圆O的切线,
∴PA=PB,
∴△BPA是等腰三角形,故A选项不符合题意.
(B)由圆的对称性可知:PD垂直平分AB,但AB不一定平分PD,故B选项符合题意.
(C)连接OB、OA,
第10页(共25页)∵PA、PB为圆O的切线,
∴∠OBP=∠OAP=90°,
∴点A、B、P在以OP为直径的圆上,故C选项不符合题意.
(D)∵△BPA是等腰三角形,PD⊥AB,
∴PC为△BPA的边AB上的中线,故D选项不符合题意.
故选:B.
【点评】本题考查切线的性质,解题的关键是熟练运用切线的性质,本题属于中等题型.
9.【分析】作CE⊥y轴于E,由矩形的性质得出CD=AB=a,AD=BC=b,∠ADC=90°,证出
∠CDE=∠DAO=x,由三角函数定义得出OD=bsinx,DE=acosx,进而得出答案.
【解答】解:作CE⊥y轴于E,如图:
∵四边形ABCD是矩形,
∴CD=AB=a,AD=BC=b,∠ADC=90°,
∴∠CDE+∠ADO=90°,
∵∠AOD=90°,
∴∠DAO+∠ADO=90°,
∴∠CDE=∠DAO=x,
∵sin∠DAO= ,cos∠CDE= ,
∴OD=AD×sin∠DAO=bsinx,DE=CD×cos∠CDE=acosx,
∴OE=DE+OD=acosx+bsinx,
∴点C到x轴的距离等于acosx+bsinx;
故选:A.
第11页(共25页)【点评】本题考查了矩形的性质、坐标与图形性质、三角函数定义等知识;熟练掌握矩形的
性质和三角函数定义是解题的关键.
10.【分析】由抛物线的开口方向判断a的符号,由抛物线与y轴的交点判断c的符号,然后根
据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【解答】解: 由图象可知:a<0,b>0,c>0,abc<0,故 错误;
由于a<0,①所以﹣2a>0. ①
②又b>0,
所以b﹣2a>0,
故 错误;
②当x=﹣1时,y=a﹣b+c<0,故 错误;
③当x=1时,y的值最大.此时,y③=a+b+c,
④而当x=n时,y=an2+bn+c,
所以a+b+c>an2+bn+c,
故a+b>an2+bn,即a+b>n(an+b),故 正确;
④
当x=3时函数值小于0,y=9a+3b+c<0,且该抛物线对称轴是直线x=﹣ =1,即a
⑤
=﹣ ,代入得9(﹣ )+3b+c<0,得2c<3b,故 正确;
⑤
故 正确.
故④选:⑤D.
【点评】本题主要考查了图象与二次函数系数之间的关系,二次函数y=ax2+bx+c系数符
第12页(共25页)号由抛物线开口方向、对称轴和抛物线与y轴的交点确定.
二、填空题(本大题共8小题,每小题4分,共32分,请将正确答案填写在答题卡相应的横线
上)
11.【分析】根据绝对值的意义,求出结果即可.
【解答】解:根据负数的绝对值等于它的相反数可得,|﹣ |= ,
故答案为: .
【点评】本题考查绝对值的意义,理解负数的绝对值等于它的相反数.
12.【分析】先提取公因式2,再根据平方差公式进行二次分解即可求得答案.
【解答】解:2x2﹣2=2(x2﹣1)=2(x+1)(x﹣1).
故答案为:2(x+1)(x﹣1).
【点评】本题考查了提公因式法,公式法分解因式,提取公因式后利用平方差公式进行二
次分解,注意分解要彻底.
13.【分析】任何多边形的外角和是360°,内角和等于外角和的2倍则内角和是720°.n边形
的内角和是(n﹣2)•180°,如果已知多边形的内角和,就可以得到一个关于边数的方程,
解方程就可以求出多边形的边数.
【解答】解:设该多边形的边数为n,
根据题意,得,(n﹣2)•180°=720°,
解得:n=6.
故这个多边形的边数为6.
故答案为:6
【点评】本题主要考查了多边形的内角和以及外角和,已知多边形的内角和求边数,可以
转化为方程的问题来解决,难度适中.
14.【分析】求出每个不等式的解集,最后求出不等式组的解集即可.
【解答】解: ,
∵解不等式 得:x≥﹣3,
解不等式 ①得:x≥﹣1,
∴不等式②组的解集为x≥﹣1,
故答案为:x≥﹣1.
第13页(共25页)【点评】本题考查了解一元一次不等式组,能根据不等式的解集找出不等式组的解集是解
此题的关键.
15.【分析】根据垂直的定义得到∠BAC=90°,根据三角形的内角和定理得到∠C=90°﹣54°
=36°,根据平行线的性质即可得到结论.
【解答】解:∵BA⊥AC,
∴∠BAC=90°,
∵∠ABC=54°,
∴∠C=90°﹣54°=36°,
∵AE∥BC,
∴∠EAC=∠C=36°,
故答案为:36.
【点评】本题考查了平行线的性质,三角形的内角和定理,熟练掌握平行线的性质是解题
的关键.
16.【分析】在平均数基本相等的前提下,方差越小产量越稳定,据此求解可得.
【解答】解:∵
甲
=
乙
≈7.5,S甲 2=0.010,S乙 2=0.002,
∴S甲 2>S乙 2,
∴乙玉米种子的产量比较稳定,
∴应该选择的玉米种子是乙,
故答案为:乙.
【点评】本题主要考查方差,解题的关键是掌握方差的意义:方差是反映一组数据的波动
大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均
值的离散程度越小,稳定性越好.
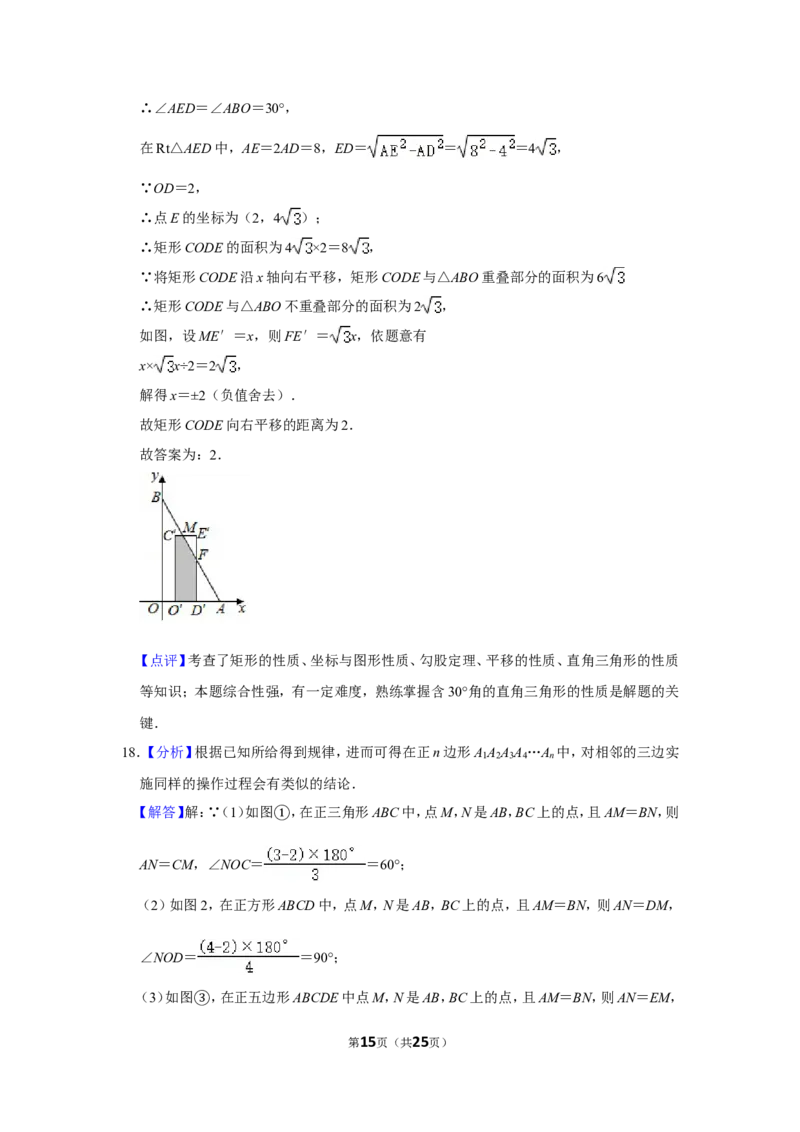
17.【分析】由已知得出AD=OA﹣OD=4,由矩形的性质得出∠AED=∠ABO=30°,在
Rt△AED中,AE=2AD=8,由勾股定理得出ED=4 ,作出图形,根据三角形面积公式
列出方程即可得出答案.
【解答】解:∵点A(6,0),
∴OA=6,
∵OD=2,
∴AD=OA﹣OD=6﹣2=4,
∵四边形CODE是矩形,
∴DE∥OC,
第14页(共25页)∴∠AED=∠ABO=30°,
在Rt△AED中,AE=2AD=8,ED= = =4 ,
∵OD=2,
∴点E的坐标为(2,4 );
∴矩形CODE的面积为4 ×2=8 ,
∵将矩形CODE沿x轴向右平移,矩形CODE与△ABO重叠部分的面积为6
∴矩形CODE与△ABO不重叠部分的面积为2 ,
如图,设ME′=x,则FE′= x,依题意有
x× x÷2=2 ,
解得x=±2(负值舍去).
故矩形CODE向右平移的距离为2.
故答案为:2.
【点评】考查了矩形的性质、坐标与图形性质、勾股定理、平移的性质、直角三角形的性质
等知识;本题综合性强,有一定难度,熟练掌握含30°角的直角三角形的性质是解题的关
键.
18.【分析】根据已知所给得到规律,进而可得在正n边形A A A A …A 中,对相邻的三边实
1 2 3 4 n
施同样的操作过程会有类似的结论.
【解答】解:∵(1)如图 ,在正三角形ABC中,点M,N是AB,BC上的点,且AM=BN,则
①
AN=CM,∠NOC= =60°;
(2)如图2,在正方形ABCD中,点M,N是AB,BC上的点,且AM=BN,则AN=DM,
∠NOD= =90°;
(3)如图 ,在正五边形ABCDE中点M,N是AB,BC上的点,且AM=BN,则AN=EM,
③
第15页(共25页)∠NOE= =108°;
…
根据以上规律,在正n边形A A A A …A 中,
1 2 3 4 n
对相邻的三边实施同样的操作过程,即点M,N是A A ,A A 上的点,
1 2 2 3
且A M=A N,A N与A M相交于O.
1 2 1 n
也有类似的结论是A N=A M,∠NOA = .
1 n n
故答案为:A N=A M,∠NOA = .
1 n n
【点评】本题考查了正多边形和圆、规律型:图形的变化类、全等三角形的判定与性质,解
决本题的关键是掌握正多边形的性质.
三、解答题(本大題关8小题,共78分,每个题目都要求在答题卡的相应位置写出计算、解答
或证明的主要步骤)
19.【分析】分别根据特殊角的三角函数值,任何非零数的零次幂定义以及绝对值的定义计算
即可.
【解答】解:原式=
=
=3.
【点评】本题主要考查了实数的运算,熟记相应定义以及特殊角的三角函数值是解答本题
的关键.
20.【分析】先计算括号内分式的减法、将除式分母因式分解,再将除法转化为乘法,最后约分
即可得.
【解答】解:原式=( ﹣ )÷
= •
= .
【点评】本题主要考查分式的混合运算,解题的关键是掌握分式的混合运算顺序和运算法
则.
21.【分析】(1)利用等边三角形的性质得到AD=AE=DE,∠EAD=∠EDA=60°,利用正方
第16页(共25页)形的性质得到AB=AD=CD,∠BAD=∠CDA=90°,所以∠EAB=∠EDC=150°,然后根
据“SAS”判定△BAE≌△CDE;
(2)先证明AB=AE,然后根据等腰三角形的性质和三角形内角和计算∠AEB的度数.
【解答】(1)证明:∵△ADE为等边三角形,
∴AD=AE=DE,∠EAD=∠EDA=60°,
∵四边形ABCD为正方形,
∴AB=AD=CD,∠BAD=∠CDA=90°,
∴∠EAB=∠EDC=150°,
在△BAE和△CDE中
,
∴△BAE≌△CDE(SAS);
(2)∵AB=AD,AD=AE,
∴AB=AE,
∴∠ABE=∠AEB,
∵∠EAB=150°,
∴∠AEB= (180°﹣150°)=15°.
【点评】本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两
条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行
四边形、矩形、菱形的一切性质.也考查了全等三角形的判定与性质和等边三角形的性质.
22.【分析】(1)将频数分布直方图中第3、4、5组数据相加可得答案;
(2)根据中位数的定义求解可得;
(3)由90≤x≤100的频数为8、80≤x<90的频数为15,据此可得答案;
(4)用总人数乘以样本中七年级成绩超过平均数76.9分的人数占被调查人数的比例即可
得.
【解答】解:(1)在这次测试中,七年级在75分以上(含75分)的有8+15+8=31(人),
故答案为:31.
(2)七年级50人成绩的中位数是第25、26个数据的平均数,而第25、26个数据分别为
77、78,
第17页(共25页)∴m= =77.5,
故答案为:77.5;
(3)在这次测试中,七年级参赛学生甲的竞赛成绩得分排名年级第24名,
故答案为:24;
(4)估计七年级成绩超过平均数76.9分的人数为500× =270(人).
【点评】本题主要考查频数分布直方图、中位数及样本估计总体,解题的关键是根据直方
图得出解题所需数据及中位数的定义和意义、样本估计总体思想的运用.
23.【分析】(1)根据题意设口罩日产量的月平均增长率为x,根据题意列出方程即可求解;
(2)结合(1)按照这个增长率,根据3月份平均日产量为24200个,即可预计4月份平均日
产量.
【解答】解:(1)设口罩日产量的月平均增长率为x,根据题意,得
20000(1+x)2=24200
解得x =﹣2.1(舍去),x =0.1=10%,
1 2
答:口罩日产量的月平均增长率为10%.
(2)24200(1+0.1)=26620(个).
答:预计4月份平均日产量为26620个.
【点评】本题考查了一元二次方程的应用,解决本题的关键是掌握增长率问题应用题的等
量关系.
24.【分析】(1)连接AE,OE,由AB是 O的直径,得到∠AEB=90°,根据直角三角形的性
质得到AD=DE,求得∠DAE=∠AE⊙D,根据切线的性质得到∠CAE+∠EAO=∠CAB=
90°,等量代换得到∠DEO=90°,于是得到结论;
(2)证明△AEC∽△BAC,列比例式可得BC的长,最后根据勾股定理可得OA的长.
【解答】(1)证明:连接AE,OE,
∵AB是 O的直径,且E在 O上,
∴∠AEB⊙=90°, ⊙
第18页(共25页)∴∠AEC=90°,
∵D为AC的中点,
∴AD=DE,
∴∠DAE=∠AED,
∵AC是 O的切线,
∴∠CAE⊙+∠EAO=∠CAB=90°,
∵OA=OE,
∴∠OAE=∠OEA,
∴∠DEA+∠OEA=90°,
即∠DEO=90°,
∴DE是 O的切线;
(2)解:⊙∵∠AEC=∠CAB=90°,∠C=∠C,
∴△AEC∽△BAC,
∴ ,
∵CA=6,CE=3.6,
∴ ,
∴BC=10,
∵∠CAB=90°,
∴AB2+AC2=BC2,
∴AB= =8,
∴OA=4,
即 O的半径OA的长是4.
【点⊙评】本题考查了切线的判定和性质,直角三角形的性质,等腰三角形的性质,相似三角
形的性质和判定,正确的识别图形是解题的关键.
25.【分析】问题背景:延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明
△BFG≌△BFE,即可得出结论:EF=AE+CF;
探究延伸1:延长FC到G,使CG=AE,连接BG,先证明△BCG≌△BAE,再证明
△BFG≌△BFE,可得出结论:EF=AE+CF;
探究延伸2:延长DC到H,使得CH=AE,连接BH,先证明△BCH≌△BAE,即可得到BE
第19页(共25页)=HB,∠ABE=∠HBC,再证明△HBF≌△EBF,即可得出EF=HF=HC+CF=AE+CF;
实际应用:连接EF,延长BF交AE的延长线于G,根据题意可转化为如下的数学问题:在
四边形GAOB中,OA=OB,∠A+∠B=180°,∠AOB=2∠EOF,∠EOF的两边分别交
AG,BG于E,F,求EF的长.再根据探究延伸2的结论:EF=AE+BF,即可得到两舰艇之
间的距离.
【解答】解:问题背景:
如图 1,延长 FC 到 G,使 CG=AE,连接 BG,先证明△BCG≌△BAE,再证明
△BFG≌△BFE,可得出结论:EF=AE+CF;
故答案为:EF=AE+CF;
探究延伸1:
上述结论仍然成立,即EF=AE+CF,理由如下:
如图2,延长FC到G,使CG=AE,连接BG,
∵CG=AE,∠BCG=∠A=90°,BC=BA,
∴△BCG≌△BAE(SAS),
∴BG=BE,∠ABE=∠CBG,
∵∠ABC=2∠EBF,
∴∠ABE+∠CBF=∠EBF,
即∠CBG+∠CBF=∠EBF,
∴∠GBF=∠EBF,
又∵BF=BF,
∴△BFG≌△BFE(SAS),
∴GF=EF,
即GC+CF=EF,
∴AE+CF=EF
∴可得出结论:EF=AE+CF;
第20页(共25页)探究延伸2:
上述结论仍然成立,即EF=AE+CF,理由:
如图3,延长DC到H,使得CH=AE,连接BH,
∵∠BAD+∠BCD=180°,∠BCH+∠BCD=180°,
∴∠BCH=∠BAE,
∵BA=BC,CH=AE,
∴△BCH≌△BAE(SAS),
∴BE=HB,∠ABE=∠HBC,
∴∠HBE=∠ABC,
又∵∠ABC=2∠MBN,
∴∠EBF=∠HBF,
∵BF=BF,
∴△HBF≌△EBF(SAS),
∴EF=HF=HC+CF=AE+CF;
实际应用:
如图4,连接EF,延长BF交AE的延长线于G,
第21页(共25页)因为舰艇甲在指挥中心(O处)北偏西30°的A处.舰艇乙在指挥中心南偏东70°的B处,
所以∠AOB=140°,
因为指挥中心观测两舰艇视线之间的夹角为 70°,所以∠EOF=70°,所以∠AOB=
2∠EOF.
依题意得,OA=OB,∠A=60°,∠B=120°,所以∠A+∠B=180°,
因此本题的实际的应用可转化为如下的数学问题:
在四边形GAOB中,OA=OB,∠A+∠B=180°,∠AOB=2∠EOF,∠EOF的两边分别交
AG,BG于E,F,求EF的长.
根据探究延伸2的结论可得:EF=AE+BF,
根据题意得,AE=75×1.2=90(海里),BF=100×1.2=120(海里),
所以EF=90+120=210(海里).
答:此时两舰艇之间的距离为210海里.
【点评】本题属于四边形综合题,主要考查了全等三角形的判定和性质,解题的关键是正
确作出辅助线构造全等三角形,解答时注意类比思想的灵活应用.
26.【分析】(1)将A点坐标代入直线与抛物线的解析式中求得k的值和b与c的关系式,再
将抛物线的顶点坐标代入求得的直线的解析式,便可求得b、c的值,进而求得E点的坐标;
(2)先根据抛物线的解析式求得C、Q点坐标,用m表示△EQM的面积,再根据S△EQM =
S△ACE 列出m的方程进行解答;
(3)取点N(0,1),则∠OAN=45°,过D作直线AN的垂线,垂足为G,DG与x轴相交于点
M,此时 AM+2DM=2DG的值最小,由2DG= 列出关于b的方程求解便可.
【解答】解:(1)∵直线y=kx﹣2与抛物线y=x2﹣bx+c(b,c为常数,b>0)的一个交点为
A(﹣1,0),
第22页(共25页)∴﹣k﹣2=0,1+b+c=0,
∴k=﹣2,c=﹣b﹣1,
∴直线y=kx﹣2的解析式为y=﹣2x﹣2,
∵抛物线y=x2﹣bx+c的顶点坐标为E( , ),
∴E( , ),
∵直线y=﹣2x﹣2与抛物线y=x2﹣bx+c(b,c为常数,b>0)的另一个交点为该抛物线的
顶点E,
∴ =﹣2× ﹣2,
解得,b=2,或b=﹣2(舍),
当b=2时,c=﹣3,
∴E(1,﹣4),
故k=﹣2,b=2,c=﹣3,E(1,﹣4);
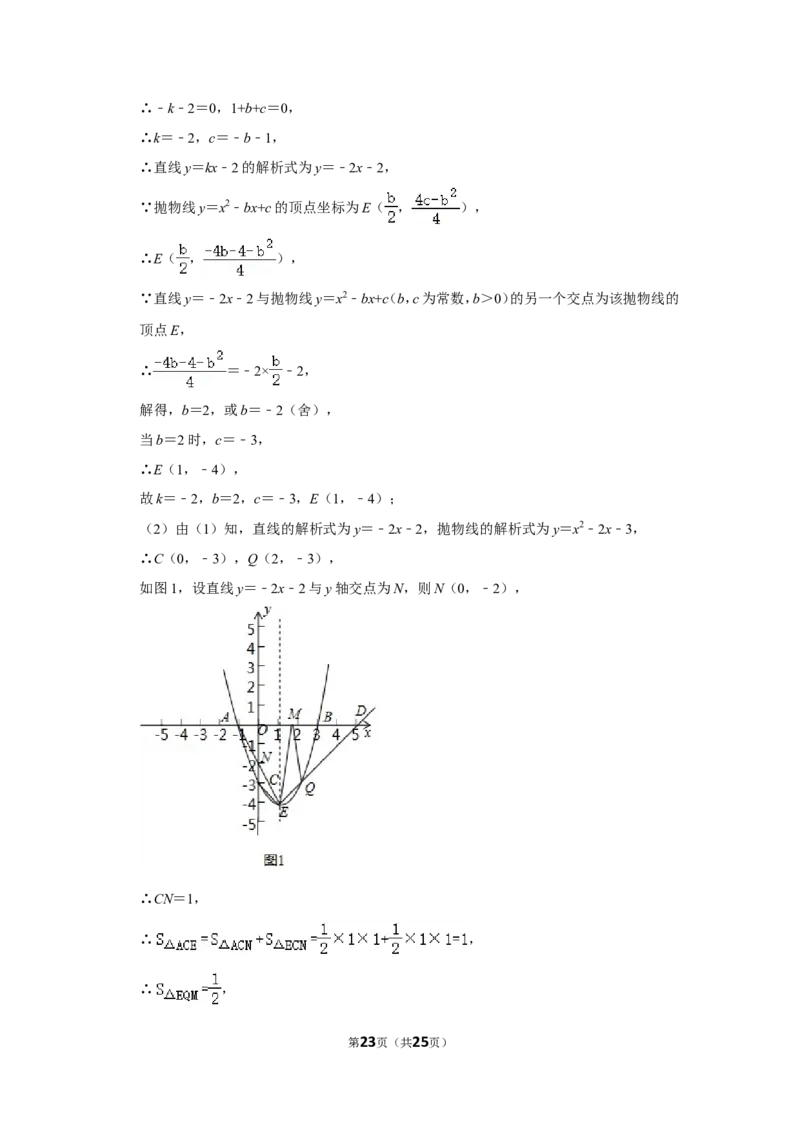
(2)由(1)知,直线的解析式为y=﹣2x﹣2,抛物线的解析式为y=x2﹣2x﹣3,
∴C(0,﹣3),Q(2,﹣3),
如图1,设直线y=﹣2x﹣2与y轴交点为N,则N(0,﹣2),
∴CN=1,
∴ ,
∴ ,
第23页(共25页)设直线EQ与x轴的交点为D,显然点M不能与点D重合,
设直线EQ的解析式为y=dx+n(d≠0),
则 ,
解得, ,
∴直线EQ的解析式为y=x﹣5,
∴D(5,0),
∴S△EQM =S△EDM ﹣S△QDM = = ,
解得,m=4,或m=6;
(3)∵点D(b+ ,y )在抛物线y=x2﹣bx﹣b﹣1上,
D
∴ ,
可知点D(b+ , )在第四象限,且在直线x=b的右侧,
∵ ,
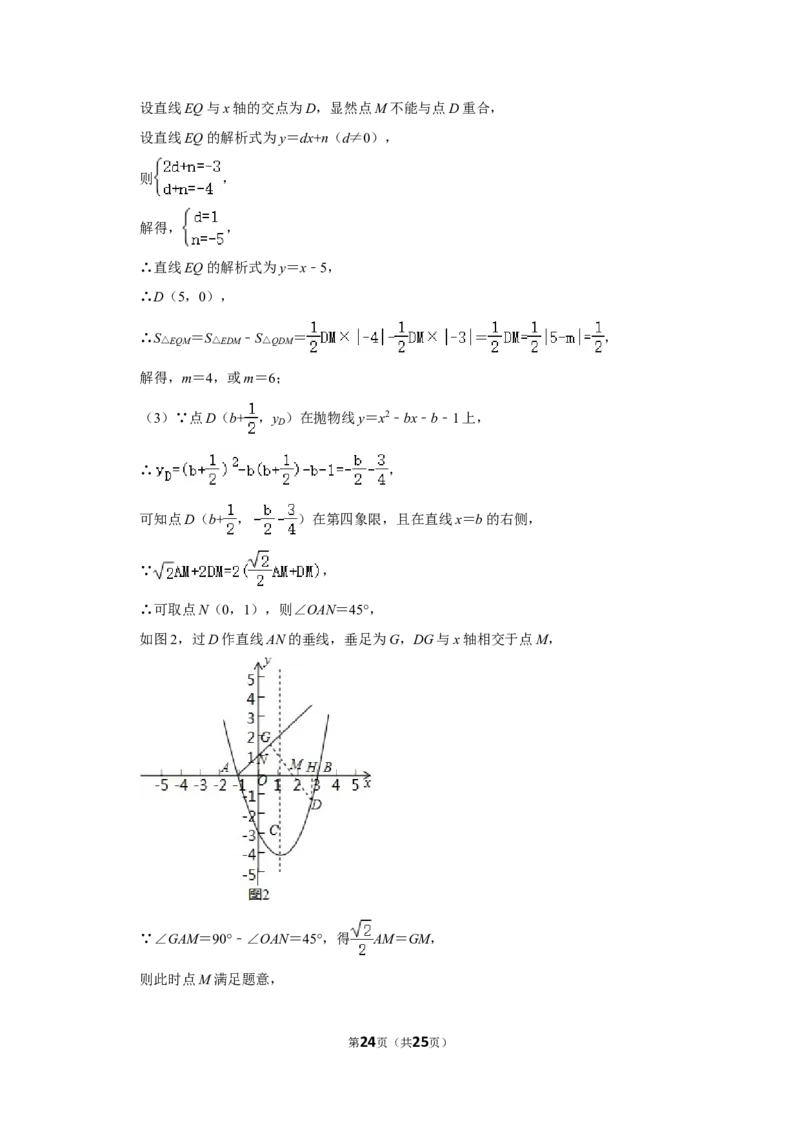
∴可取点N(0,1),则∠OAN=45°,
如图2,过D作直线AN的垂线,垂足为G,DG与x轴相交于点M,
∵∠GAM=90°﹣∠OAN=45°,得 AM=GM,
则此时点M满足题意,
第24页(共25页)过D作DH⊥x轴于点H,则点H(b+ ,0),
在Rt△MDH中,可知∠DMH=∠MDH=45°,
∴DH=MH,DM= MH,
∵点M(m,0),
∴0﹣( )=(b+ )﹣m,
解得,m= ,
∵ ,
∴ ,
解得,b=3,
此时,m= ,符合题意,
∴b=3.
【点评】本题是二次函数的综合题,主要考查了待定系数法,二次函数的图象与性质,三角
形面积公式,等腰直角三角形的性质,第(2)小题关键是由面积关系列出m的方程,第(3)
小题关键是确定 AM+2DM的最小值为2DG的值.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/9/16 11:10:46;用户:18366185883;邮箱:18366185883;学号:22597006
第25页(共25页)