文档内容
2020年湖南省益阳市中考数学试卷
一、选择题(本题共10个小题,每小题4分,共40分.每小题给出的四个选项中,只有一项是
符合题目要求的)
1.(4分)四个实数1,0, ,﹣3中,最大的数是( )
A.1 B.0 C. D.﹣3
2.(4分)将不等式组 的解集在数轴上表示,正确的是( )
A. B.
C. D.
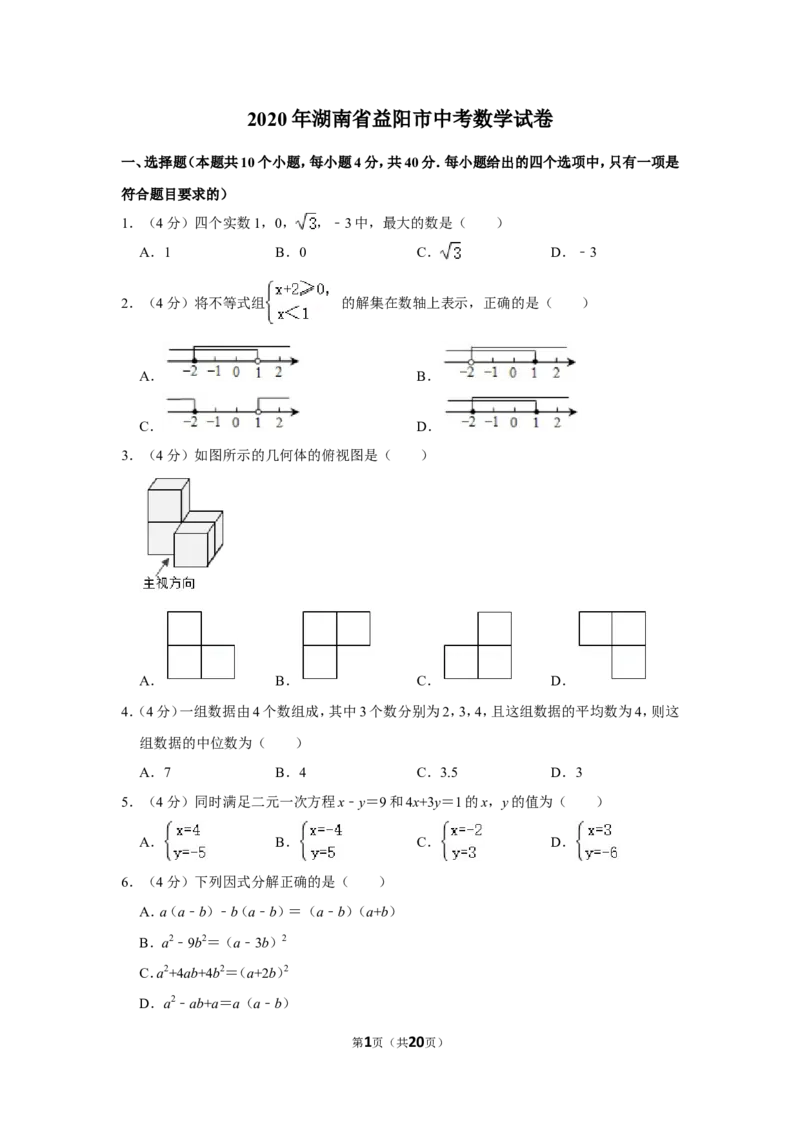
3.(4分)如图所示的几何体的俯视图是( )
A. B. C. D.
4.(4分)一组数据由4个数组成,其中3个数分别为2,3,4,且这组数据的平均数为4,则这
组数据的中位数为( )
A.7 B.4 C.3.5 D.3
5.(4分)同时满足二元一次方程x﹣y=9和4x+3y=1的x,y的值为( )
A. B. C. D.
6.(4分)下列因式分解正确的是( )
A.a(a﹣b)﹣b(a﹣b)= (a﹣b)(a+b)
B.a2﹣9b2=(a﹣3b)2
C.a2+4ab+4b2=(a+2b)2
D.a2﹣ab+a=a(a﹣b)
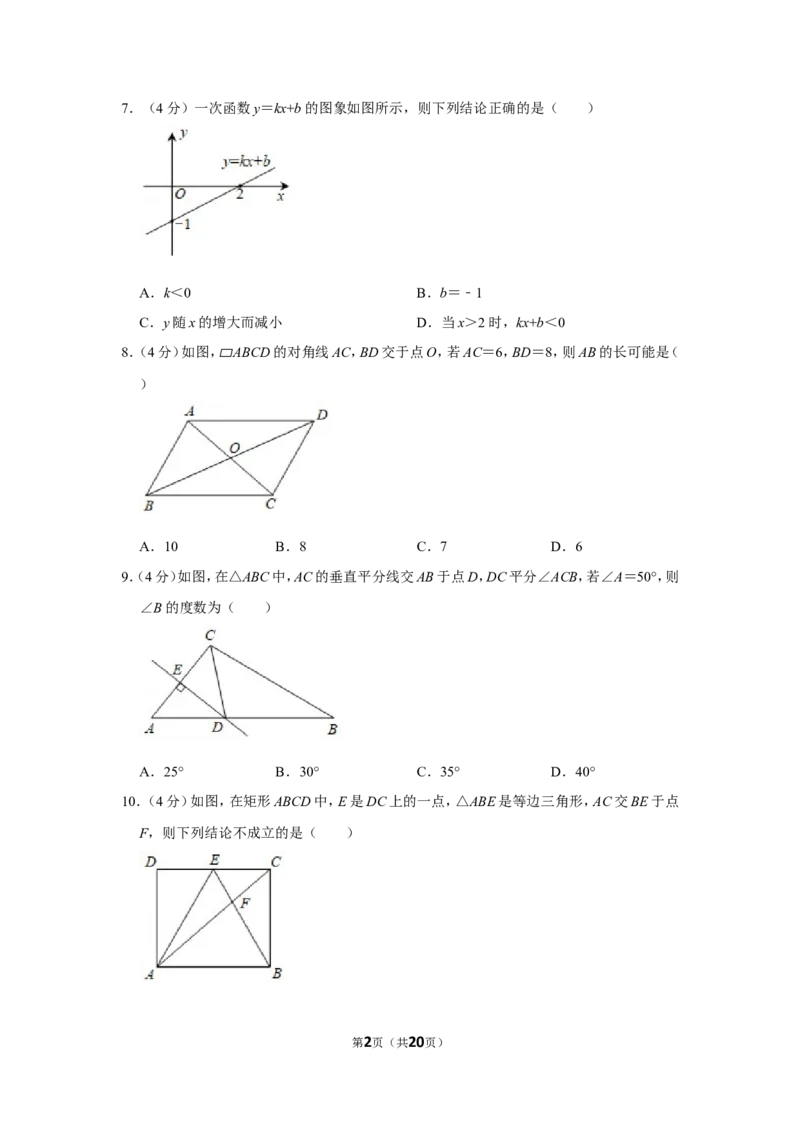
第1页(共20页)7.(4分)一次函数y=kx+b的图象如图所示,则下列结论正确的是( )
A.k<0 B.b=﹣1
C.y随x的增大而减小 D.当x>2时,kx+b<0
8.(4分)如图, ABCD的对角线AC,BD交于点O,若AC=6,BD=8,则AB的长可能是(
) ▱
A.10 B.8 C.7 D.6
9.(4分)如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB,若∠A=50°,则
∠B的度数为( )
A.25° B.30° C.35° D.40°
10.(4分)如图,在矩形ABCD中,E是DC上的一点,△ABE是等边三角形,AC交BE于点
F,则下列结论不成立的是( )
第2页(共20页)A.∠DAE=30° B.∠BAC=45° C. D.
二、填空题(本题共8个小题,每小题4分,共32分,请将答案填在答题卡中对应题号的横线
上)
11.(4分)我国北斗全球导航系统最后一颗组网卫星于2020年6月30日成功定点于距离地
球36000千米的地球同步轨道.将“36000”用科学记数法表示为 .
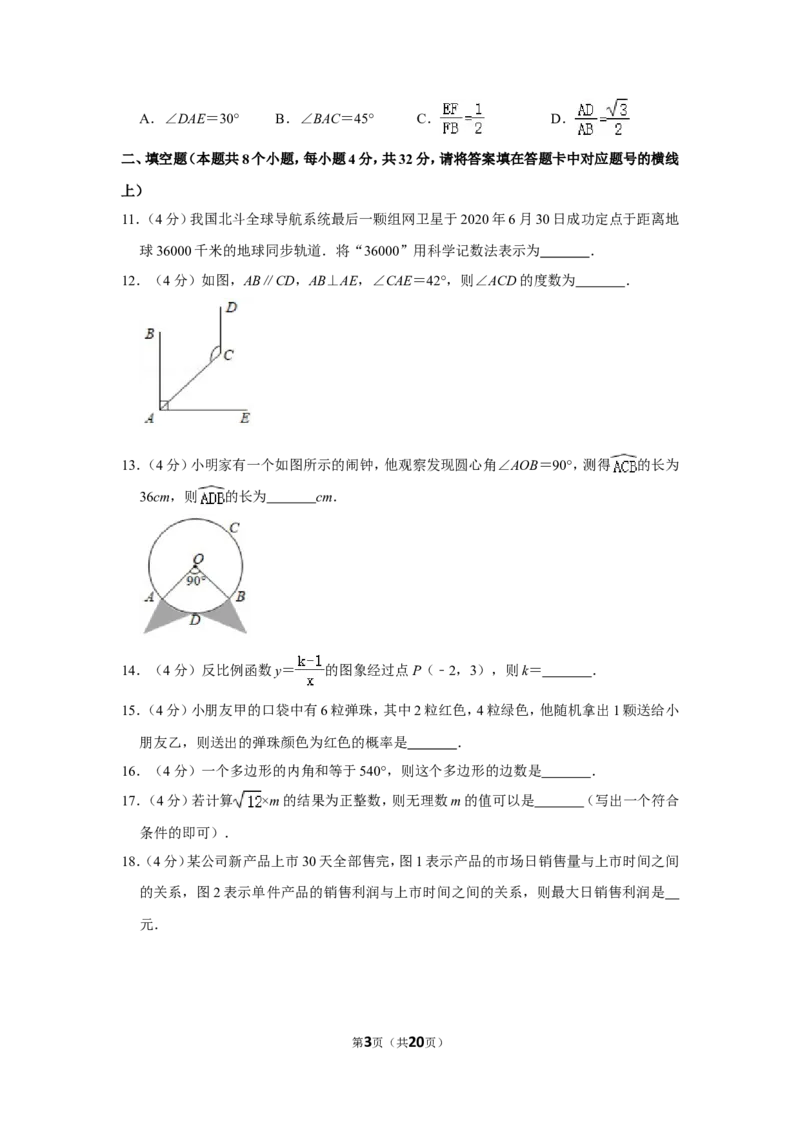
12.(4分)如图,AB∥CD,AB⊥AE,∠CAE=42°,则∠ACD的度数为 .
13.(4分)小明家有一个如图所示的闹钟,他观察发现圆心角∠AOB=90°,测得 的长为
36cm,则 的长为 cm.
14.(4分)反比例函数y= 的图象经过点P(﹣2,3),则k= .
15.(4分)小朋友甲的口袋中有6粒弹珠,其中2粒红色,4粒绿色,他随机拿出1颗送给小
朋友乙,则送出的弹珠颜色为红色的概率是 .
16.(4分)一个多边形的内角和等于540°,则这个多边形的边数是 .
17.(4分)若计算 ×m的结果为正整数,则无理数m的值可以是 (写出一个符合
条件的即可).
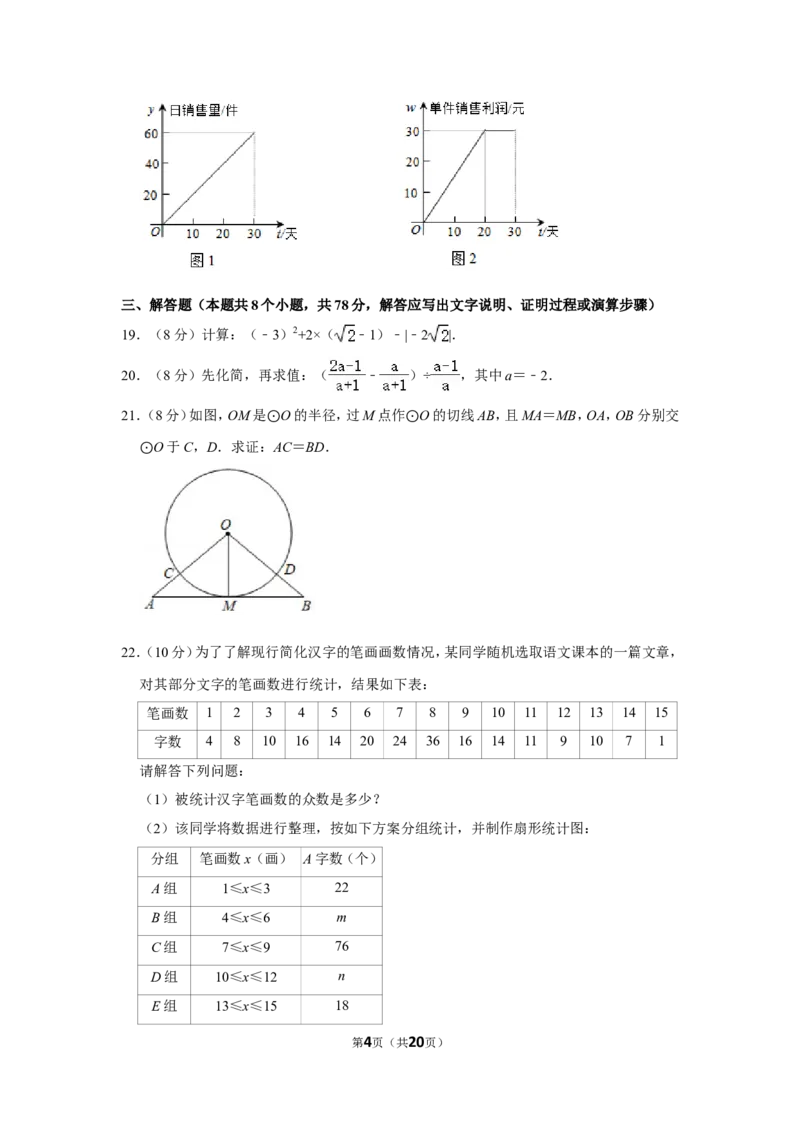
18.(4分)某公司新产品上市30天全部售完,图1表示产品的市场日销售量与上市时间之间
的关系,图2表示单件产品的销售利润与上市时间之间的关系,则最大日销售利润是
元.
第3页(共20页)三、解答题(本题共8个小题,共78分,解答应写出文字说明、证明过程或演算步骤)
19.(8分)计算:(﹣3)2+2×( ﹣1)﹣|﹣2 |.
20.(8分)先化简,再求值:( ﹣ )÷ ,其中a=﹣2.
21.(8分)如图,OM是 O的半径,过M点作 O的切线AB,且MA=MB,OA,OB分别交
O于C,D.求证:⊙AC=BD. ⊙
⊙
22.(10分)为了了解现行简化汉字的笔画画数情况,某同学随机选取语文课本的一篇文章,
对其部分文字的笔画数进行统计,结果如下表:
笔画数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
字数 4 8 10 16 14 20 24 36 16 14 11 9 10 7 1
请解答下列问题:
(1)被统计汉字笔画数的众数是多少?
(2)该同学将数据进行整理,按如下方案分组统计,并制作扇形统计图:
分组 笔画数x(画) A字数(个)
A组 1≤x≤3 22
B组 4≤x≤6 m
C组 7≤x≤9 76
D组 10≤x≤12 n
E组 13≤x≤15 18
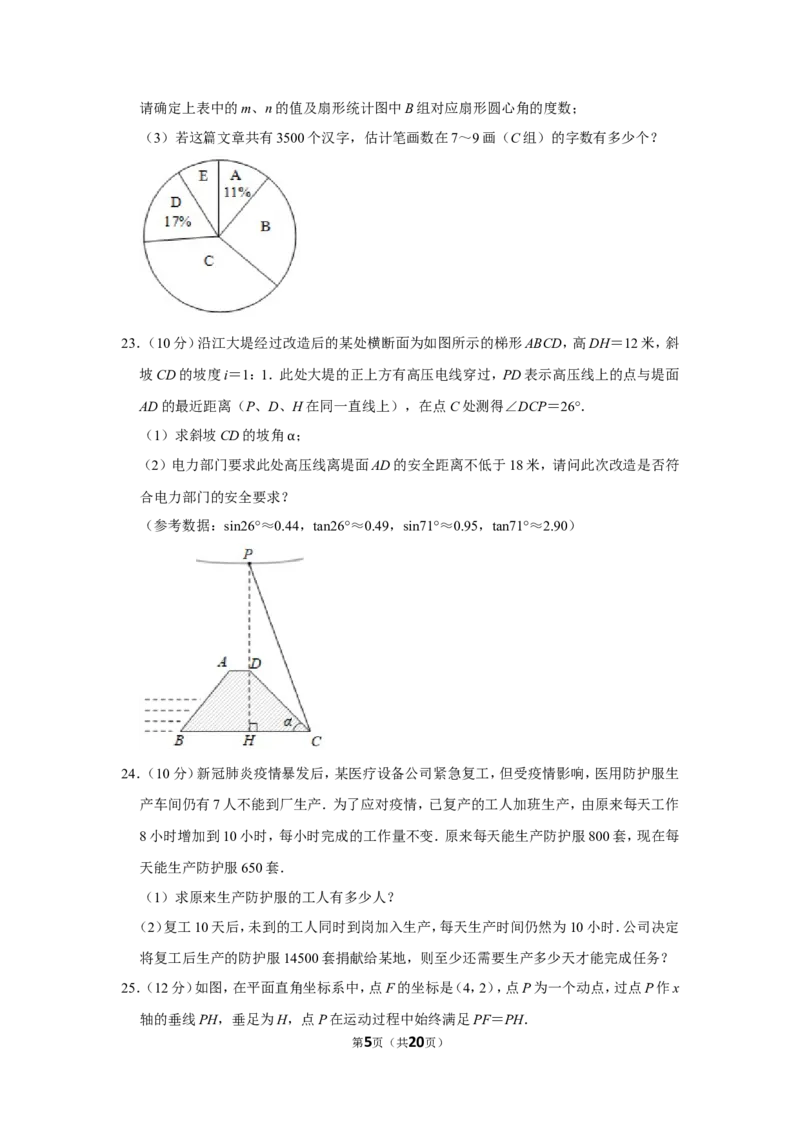
第4页(共20页)请确定上表中的m、n的值及扇形统计图中B组对应扇形圆心角的度数;
(3)若这篇文章共有3500个汉字,估计笔画数在7~9画(C组)的字数有多少个?
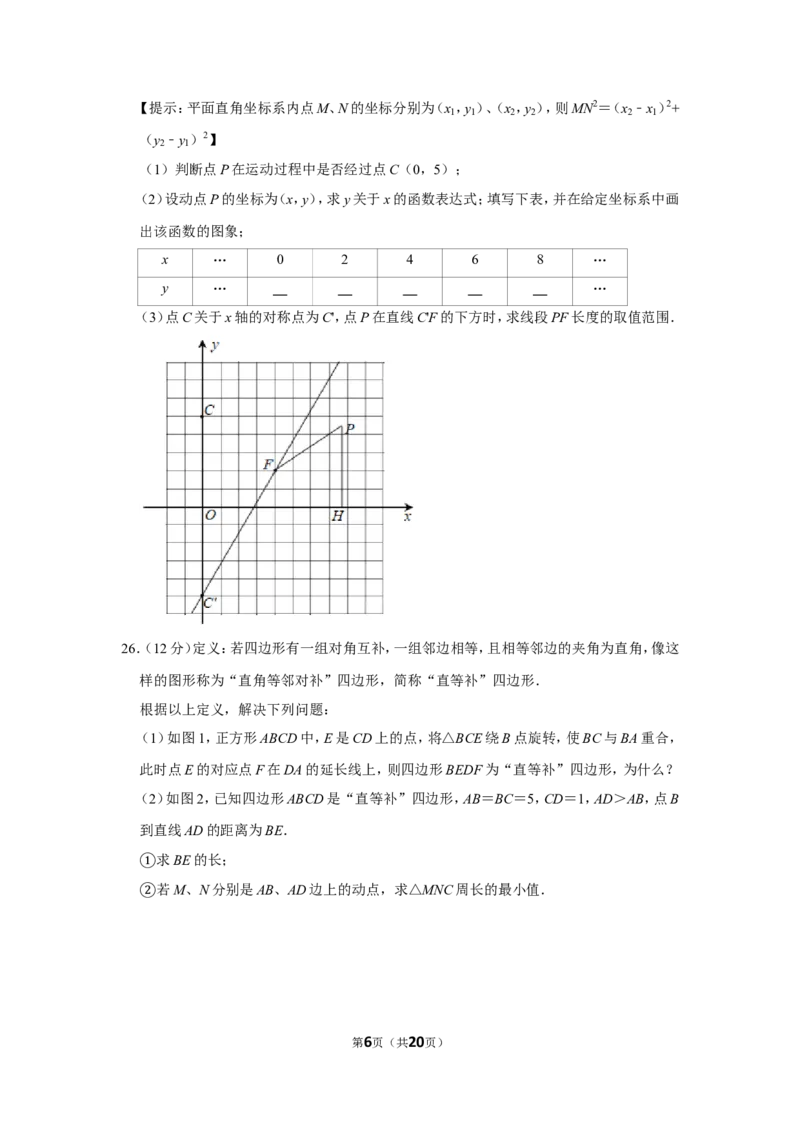
23.(10分)沿江大堤经过改造后的某处横断面为如图所示的梯形ABCD,高DH=12米,斜
坡CD的坡度i=1:1.此处大堤的正上方有高压电线穿过,PD表示高压线上的点与堤面
AD的最近距离(P、D、H在同一直线上),在点C处测得∠DCP=26°.
(1)求斜坡CD的坡角 ;
(2)电力部门要求此处高α压线离堤面AD的安全距离不低于18米,请问此次改造是否符
合电力部门的安全要求?
(参考数据:sin26°≈0.44,tan26°≈0.49,sin71°≈0.95,tan71°≈2.90)
24.(10分)新冠肺炎疫情暴发后,某医疗设备公司紧急复工,但受疫情影响,医用防护服生
产车间仍有7人不能到厂生产.为了应对疫情,已复产的工人加班生产,由原来每天工作
8小时增加到10小时,每小时完成的工作量不变.原来每天能生产防护服800套,现在每
天能生产防护服650套.
(1)求原来生产防护服的工人有多少人?
(2)复工10天后,未到的工人同时到岗加入生产,每天生产时间仍然为10小时.公司决定
将复工后生产的防护服14500套捐献给某地,则至少还需要生产多少天才能完成任务?
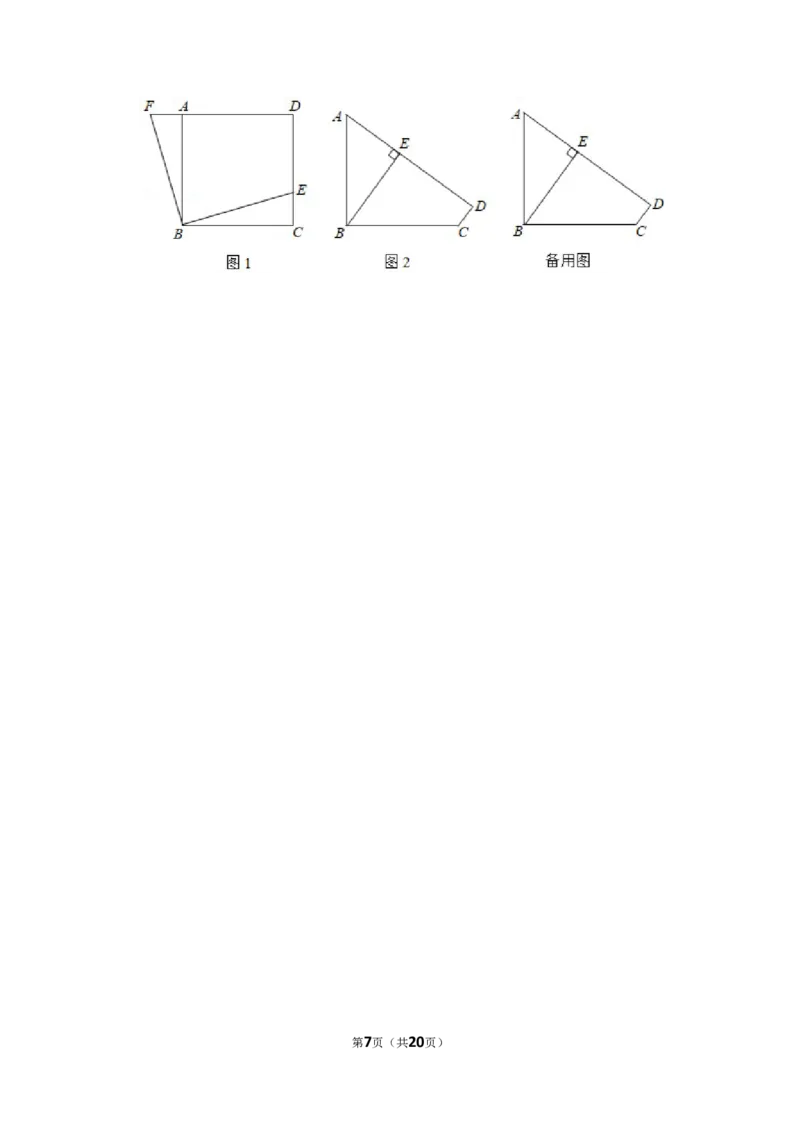
25.(12分)如图,在平面直角坐标系中,点F的坐标是(4,2),点P为一个动点,过点P作x
轴的垂线PH,垂足为H,点P在运动过程中始终满足PF=PH.
第5页(共20页)【提示:平面直角坐标系内点M、N的坐标分别为(x ,y )、(x ,y ),则MN2=(x ﹣x )2+
1 1 2 2 2 1
(y ﹣y )2】
2 1
(1)判断点P在运动过程中是否经过点C(0,5);
(2)设动点P的坐标为(x,y),求y关于x的函数表达式;填写下表,并在给定坐标系中画
出该函数的图象;
x … 0 2 4 6 8 …
y … …
(3)点C关于x轴的对称点为C',点P在直线C'F的下方时,求线段PF长度的取值范围.
26.(12分)定义:若四边形有一组对角互补,一组邻边相等,且相等邻边的夹角为直角,像这
样的图形称为“直角等邻对补”四边形,简称“直等补”四边形.
根据以上定义,解决下列问题:
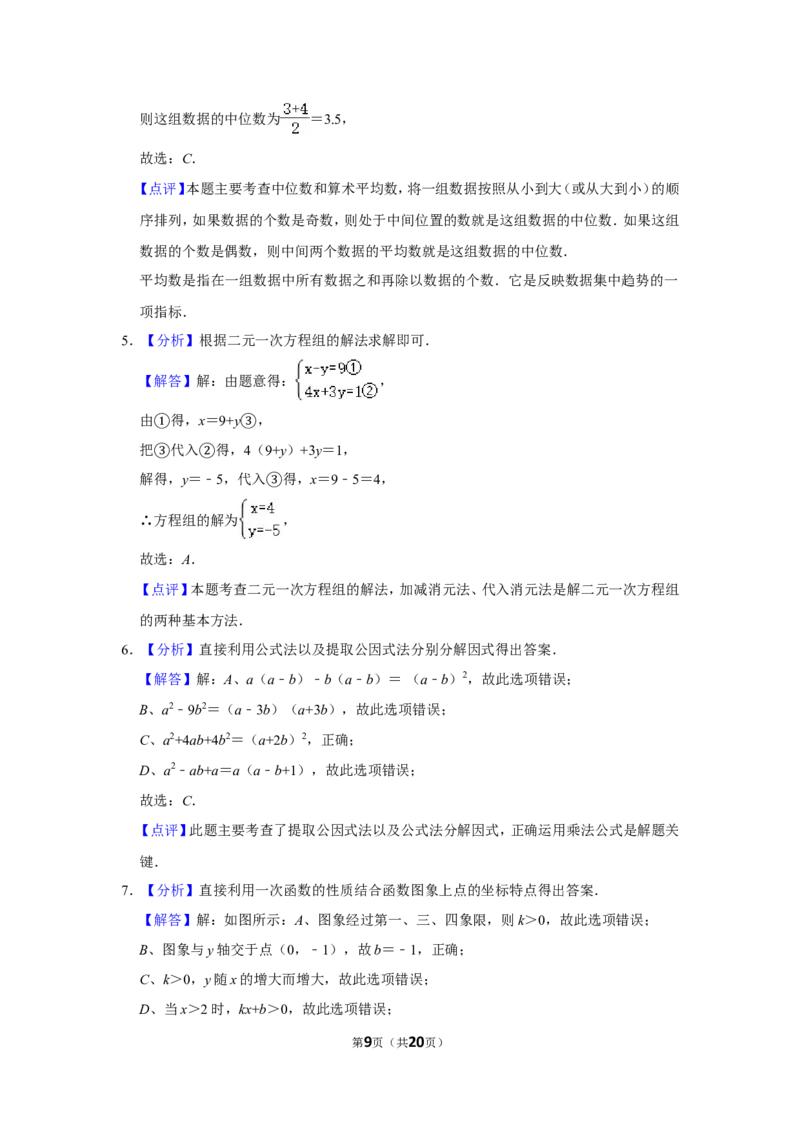
(1)如图1,正方形ABCD中,E是CD上的点,将△BCE绕B点旋转,使BC与BA重合,
此时点E的对应点F在DA的延长线上,则四边形BEDF为“直等补”四边形,为什么?
(2)如图2,已知四边形ABCD是“直等补”四边形,AB=BC=5,CD=1,AD>AB,点B
到直线AD的距离为BE.
求BE的长;
①若M、N分别是AB、AD边上的动点,求△MNC周长的最小值.
②
第6页(共20页)第7页(共20页)2020年湖南省益阳市中考数学试卷
参考答案与试题解析
一、选择题(本题共10个小题,每小题4分,共40分.每小题给出的四个选项中,只有一项是
符合题目要求的)
1.【分析】直接利用实数的比较大小的方法分析得出答案.
【解答】解:四个实数1,0, ,﹣3中,
﹣3<0<1< ,
故最大的数是: .
故选:C.
【点评】此题主要考查了实数运算,正确掌握实数比较大小的方法是解题关键.
2.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、
大大小小无解了确定不等式组的解集,从而得出答案.
【解答】解:解不等式x+2≥0,得:x≥﹣2,
又x<1,
∴不等式组的解集为﹣2≤x<1,
将不等式组的解集表示在数轴上如下:
故选:A.
【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知
“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.
3.【分析】从上面看该几何体所得到的图形即为该几何体的俯视图.
【解答】解:从上面看该几何体,选项D的图形符合题意,
故选:D.
【点评】本题考查简单组合体的三视图,俯视图是从上面看所得到的图形,也可以理解为
从上面对该几何体正投影所得到的图形.
4.【分析】先根据算术平均数的概念求出另外一个数据,从而得出这组数据,再利用中位数的
概念求解可得.
【解答】解:根据题意知,另外一个数为4×4﹣(2+3+4)=7,
所以这组数据为2,3,4,7,
第8页(共20页)则这组数据的中位数为 =3.5,
故选:C.
【点评】本题主要考查中位数和算术平均数,将一组数据按照从小到大(或从大到小)的顺
序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数.如果这组
数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一
项指标.
5.【分析】根据二元一次方程组的解法求解即可.
【解答】解:由题意得: ,
由 得,x=9+y ,
把①代入 得,③4(9+y)+3y=1,
解③得,y=②﹣5,代入 得,x=9﹣5=4,
③
∴方程组的解为 ,
故选:A.
【点评】本题考查二元一次方程组的解法,加减消元法、代入消元法是解二元一次方程组
的两种基本方法.
6.【分析】直接利用公式法以及提取公因式法分别分解因式得出答案.
【解答】解:A、a(a﹣b)﹣b(a﹣b)= (a﹣b)2,故此选项错误;
B、a2﹣9b2=(a﹣3b)(a+3b),故此选项错误;
C、a2+4ab+4b2=(a+2b)2,正确;
D、a2﹣ab+a=a(a﹣b+1),故此选项错误;
故选:C.
【点评】此题主要考查了提取公因式法以及公式法分解因式,正确运用乘法公式是解题关
键.
7.【分析】直接利用一次函数的性质结合函数图象上点的坐标特点得出答案.
【解答】解:如图所示:A、图象经过第一、三、四象限,则k>0,故此选项错误;
B、图象与y轴交于点(0,﹣1),故b=﹣1,正确;
C、k>0,y随x的增大而增大,故此选项错误;
D、当x>2时,kx+b>0,故此选项错误;
第9页(共20页)故选:B.
【点评】此题主要考查了一次函数与一元一次不等式,正确数形结合分析是解题关键.
8.【分析】根据三角形三边关系:任意两边之和大于第三边,任意两边之差小于第三边,可得
出AB的取值范围,进而得出结论.
【解答】解:∵四边形ABCD是平行四边形,
∴OA= AC=3,OB= BD=4,
在△AOB中:4﹣3<AB<4+3,
即1<AB<7,
∴AB的长可能为6.
故选:D.
【点评】本题考查的了平行四边形的性质和三角形的三边关系.解题时注意:平行四边形
对角线互相平分;三角形中任意两边之和大于第三边,任意两边之差小于第三边.
9.【分析】依据线段垂直平分线的性质,即可得到∠A=∠ACD,再根据角平分线的定义,即
可得出∠ACB的度数,根据三角形内角和定理,即可得到∠B的度数.
【解答】解:∵DE垂直平分AC,
∴AD=CD,
∴∠A=∠ACD
又∵CD平分∠ACB,
∴∠ACB=2∠ACD=100°,
∴∠B=180°﹣∠A﹣∠ACB=180°﹣50°﹣100°=30°,
故选:B.
【点评】本题主要考查了线段垂直平分线的性质以及三角形内角和定理,线段垂直平分线
上任意一点,到线段两端点的距离相等.
10.【分析】由矩形的性质和等边三角形的性质可得AB=AE=BE,∠EAB=∠EBA=60°,AD
=BC,∠DAB=∠CBA=90°,AB∥CD,AB=CD,可得∠DAE=∠CBE=30°,由锐角三角
函数可求cos∠DAC= = ,由“SAS”可证∴△ADE≌△BCE,可得DE=CE
= CD= AB,通过证明△ABF∽△CEF,可得 ,通过排除法可求解.
【解答】解:∵四边形ABCD是矩形,△ABE是等边三角形,
第10页(共20页)∴AB=AE=BE,∠EAB=∠EBA=60°,AD=BC,∠DAB=∠CBA=90°,AB∥CD,AB=
CD,
∴∠DAE=∠CBE=30°,故选项A不合题意,
∴cos∠DAE= = ,故选项D不合题意,
在△ADE和△BCE中,
,
∴△ADE≌△BCE(SAS),
∴DE=CE= CD= AB,
∵AB∥CD,
∴△ABF∽△CEF,
∴ ,故选项C不合题意,
故选:B.
【点评】本题考查了相似三角形的判定和性质,等边三角形的性质,矩形的性质,全等三角
形的判定和性质,熟练运用这些性质进行推理是本题的关键.
二、填空题(本题共8个小题,每小题4分,共32分,请将答案填在答题卡中对应题号的横线
上)
11.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是
易错点,由于36000有5位,所以可以确定n=5﹣1=4.
【解答】解:36000=3.6×104.
故答案为:3.6×104.
【点评】此题考查科学记数法表示较大的数的方法,准确确定a与n值是关键.
12.【分析】直接利用平行线的性质结合垂直定义得出∠BAC度数以及∠ACD的度数.
【解答】解:∵AB⊥AE,∠CAE=42°,
∴∠BAC=90°﹣42°=48°,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∴∠ACD=132°.
故答案为:132°.
第11页(共20页)【点评】此题主要考查了平行线的性质,正确得出∠BAC度数是解题关键.
13.【分析】根据 的长为36cm,可得半径OA,进而可得 的长.
【解答】解:
法一:∵ 的长为36cm,
∴ =36,
∴OA= ,
则 的长为: = × =12(cm);
法二:∵ 与 所对应的圆心角度数的比值为270°:90°=3:1,
∴ 与 的弧长之比为3:1,
∴ 的弧长为36÷3=12(cm),
故答案为:12.
【点评】本题考查了弧长的计算,解决本题的关键是掌握弧长公式.
14.【分析】直接把点(﹣2,3)代入反比例函数y= 求出k的值即可.
【解答】解:∵反比例函数y= 的图象经过点(﹣2,3),
∴3= ,解得k=﹣5.
故答案是:﹣5.
【点评】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐
标一定适合此函数的解析式是解答此题的关键.
15.【分析】用红色弹珠的数量除以弹珠的总个数即可得.
【解答】解:∵口袋中有6粒弹珠,随机拿出1颗共有6种等可能结果,其中送出的弹珠颜
色为红色的有2种结果,
∴送出的弹珠颜色为红色的概率是 = ,
故答案为: .
【点评】本题主要考查概率公式,解题的关键是掌握随机事件A的概率P(A)=事件A可
能出现的结果数÷所有可能出现的结果数.
16.【分析】n边形的内角和公式为(n﹣2)•180°,由此列方程求n.
第12页(共20页)【解答】解:设这个多边形的边数是n,
则(n﹣2)•180°=540°,
解得n=5,
故答案为:5.
【点评】本题考查了多边形外角与内角.此题比较简单,只要结合多边形的内角和公式来
寻求等量关系,构建方程即可求解.
17.【分析】直接利用二次根式的性质得出符合题意的答案.
【解答】解:若计算 ×m的结果为正整数,则无理数m的值可以是: (答案不唯一).
故答案为: (答案不唯一).
【点评】此题主要考查了二次根式的乘除法,正确掌握二次根式的性质是解题关键.
18.【分析】根据题意和函数图象中的数据,利用分类讨论的方法,可以求得最大日销售利润,
从而可以解答本题.
【解答】解:设日销售量y与销售天数t之间的函数关系式为y=kx,
30k=60,得k=2,
即日销售量y与销售天数t之间的函数关系式为y=2t,
当0<t≤20时,设单件的利润w与t之间的函数关系式为w=at,
20a=30,得a=1.5,
即当0<t≤20时,单件的利润w与t之间的函数关系式为w=1.5t,
当20<t≤30时,单件的利润w与t之间的函数关系式为w=30,
设日销售利润为W元,
当0<t≤20时,W=1.5t×2t=3t2,
故当t=20时,W取得最大值,此时W=1200,
当20<t≤30时,W=30×2t=60t,
故当t=30时,W取得最大值,此时W=1800,
综上所述,最大日销售利润为1800元,
故答案为:1800.
【点评】本题考查二次函数的应用,解答本题的关键是明确题意,利用二次函数的性质和
数形结合的思想解答.
三、解答题(本题共8个小题,共78分,解答应写出文字说明、证明过程或演算步骤)
19.【分析】直接利用绝对值的性质和实数混合运算法则分别化简得出答案.
【解答】解:原式=9+2 ﹣2﹣2
第13页(共20页)=7.
【点评】此题主要考查了实数运算,正确化简各数是解题关键.
20.【分析】先计算括号内分式的减法,再将除法转化为乘法,约分即可化简原式,最后把a的
值代入计算可得.
【解答】解:原式= ÷
= •
= ,
当a=﹣2时,原式= = =2.
【点评】本题主要考查分式的化简求值,解题的关键是掌握分式的混合运算顺序和运算法
则.
21.【分析】由切线的性质得出OM⊥AB,又MA=MB,则△ABO是等腰三角形,得出OA=
OB,即可得出结论.
【解答】证明:∵OM是 O的半径,过M点作 O的切线AB,
∴OM⊥AB, ⊙ ⊙
∵MA=MB,
∴△ABO是等腰三角形,
∴OA=OB,
∵OC=OD,
∴OA﹣OC=OB﹣OD,即:AC=BD.
【点评】本题考查了切线的性质、等腰三角形的判定与性质等知识;熟练掌握切线的性质
是解题的关键.
22.【分析】(1)根据众数的定义求解可得;
(2)根据第1个表格可得m、n的值及被抽查汉字的个数,再用360°乘以B组频数占总数
的比例即可得;
(3)用汉字的总个数乘以样本中C组频数占样本容量的比例可得.
【解答】解:(1)被统计汉字笔画数的众数是8画;
(2)m=16+14+20=50,n=14+11+9=34,
∵被抽查的汉字个数为4+8+10+16+14+20+24+36+16+14+11+9+10+7+1=200(个),
第14页(共20页)∴扇形统计图中B组对应扇形圆心角的度数为360°× =90°;
(3)估计笔画数在7~9画(C组)的字数有3500× =1330(个).
【点评】本题主要考查扇形统计图、用样本估计总体、频数(率)分布表及众数,解题的关键
是掌握利用样本估计总体思想的运用及众数的概念.
23.【分析】(1)根据斜坡CD的坡度i=1:1,可得tan =DH:CH=1:1=1,进而可得 的度
数; α α
(2)由(1)可得,CH=DH=12,=45°.所以∠PCH=71°,再根据锐角三角函数可得PD
的值,与18进行比较即可得到此α次改造是否符合电力部门的安全要求.
【解答】解:(1)∵斜坡CD的坡度i=1:1,
∴tan =DH:CH=1:1=1,
∴ =α45°.
答α:斜坡CD的坡角 为45°;
(2)由(1)可知:α
CH=DH=12, =45°.
∴∠PCH=∠PCαD+ =26°+45°=71°,
α
在Rt△PCH中,∵tan∠PCH= = ≈2.90,
∴PD≈22.8(米).
22.8>18,
答:此次改造符合电力部门的安全要求.
【点评】本题考查了解直角三角形的应用﹣坡度坡角问题,解决本题的关键是掌握坡度坡
角定义.
24.【分析】(1)设原来生产防护服的工人有x人,根据每人每小时完成的工作量不变列出关
于x的方程,求解即可;
(2)设还需要生产y天才能完成任务.根据前面10天完成的工作量+后面y天完成的工作
量≥14500列出关于y的不等式,求解即可.
【解答】解:(1)设原来生产防护服的工人有x人,
由题意得, = ,
解得:x=20.
第15页(共20页)经检验,x=20是原方程的解.
答:原来生产防护服的工人有20人;
(2)设还需要生产y天才能完成任务.
=5(套),
即每人每小时生产5套防护服.
由题意得,10×650+20×5×10y≥14500,
解得y≥8.
答:至少还需要生产8天才能完成任务.
【点评】本题考查分式方程的应用,一元一次不等式的应用,分析题意,找到合适的数量关
系是解决问题的关键.
25.【分析】(1)当P与C(0,5)重合,证明PH=PF即可解决问题.
(2)根据PF2=PH2,根据函数关系式即可解决问题.
(3)求出直线FC′的解析式,求出直线FC′与抛物线的交点坐标即可判断.
【解答】解:(1)当P与C(0,5)重合,
∴PH=5,PF= =5,
∴PH=PF,
∴点P运动过程中经过点C.
(2)由题意:y2=(x﹣4)2+(y﹣2)2,
整理得,y= x2﹣2x+5,
∴函数解析式为y= x2﹣2x+5,
当x=0时,y=5,
当x=2时,y=2,
当x=4时,y=1,
当x=6时,y=2,
当x=8时,y=5,
函数图象如图所示:
第16页(共20页)故答案为5,2,1,2,5.
(3)由题意C′(0,﹣5),F(4,2),
∴直线FC′的解析式为y= x﹣5,设抛物线交直线FC′于G,K.
由 ,解得 或 ,
∴G( , ),K( , ),
观察图象可知满足条件的PF长度的取值范围为1≤PF< .
【点评】本题属于二次函数综合题,考查了二次函数的性质,一次函数的性质等知识,解题
的关键是理解题意,灵活运用所学知识解决问题,属于中考压轴题.
26.【分析】(1)由旋转性质得BE=BF,再证明∠EBF=90°,∠EBF+∠D=180°便可;
(2) 过点C作CF⊥BE于点F,证明△BCF≌△ABE得CF=BE,设BE=x,在Rt△BCF
中,①则勾股定理列出x的方程解答便可;
延长CB到F,使得BF=BC,延长CD到G,使得CD=DG,连接FG,分别与AB、AD交
第17页(共20页)
②于点M、N,求出FG便是△MNC的最小周长.
【解答】解:(1)∵四边形ABCD是正方形,
∴∠ABC=∠BAD=∠C=∠D=90°,
∵将△BCE绕B点旋转,使BC与BA重合,此时点E的对应点F在DA的延长线上,
∴BE=BF,∠CBE=∠ABF,
∴∠EBF=∠ABC=90°,
∴∠EBF+∠D=180°,
∴四边形BEDF为“直等补”四边形;
(2) 过C作CF⊥BF于点F,如图1,
则∠C①FE=90°,
∵四边形ABCD是“直等补”四边形,AB=BC=5,CD=1,AD>AB,
∴∠ABC=90°,∠ABC+∠D=180°,
∴∠D=90°,
∵BE⊥AD,
∴∠DEF=90°,
∴四边形CDEF是矩形,
∴EF=CD=1,
∵∠ABE+∠A=∠CBE+∠ABE=90°,
∴∠A=∠CBF,
∵∠AEB=∠BFC=90°,AB=BC=5,
∴△ABE≌△BCF(AAS),
∴BE=CF,
设BE=CF=x,则BF=x﹣1,
∵CF2+BF2=BC2,
∴x2+(x﹣1)2=52,
解得,x=4,或x=﹣3(舍),
第18页(共20页)∴BE=4;
如图2,延长CB到F,使得BF=BC,延长CD到G,使得CD=DG,连接FG,分别与
②AB、AD交于点M、N,过G作GH⊥BC,与BC的延长线交于点H.
则BC=BF=5,CD=DG=1,
∵∠ABC=∠ADC=90°,
∴CM=FM,CN=GN,
∴△MNC的周长=CM+MN+CN=FM+MN+GN=FG的值最小,
∵四边形ABCD是“直等补”四边形,
∴∠A+∠BCD=180°,
∵∠BCD+∠HCG=180°,
∴∠A=∠HCG,
∵∠AEB=∠CHG=90°,
∴△ABE∽△CGH,
∴
∵AB=5,BE=4,
∴AE= ,
∴ ,
∴GH= ,CH= ,
∴FH=FC+CH= ,
∴FG= =8 ,
∴△MNC周长的最小值为8 .
第19页(共20页)【点评】本题是四边形的一个综合题,主要考查新定义,勾股定理,全等三角形的性质与判
定,正方形的性质,矩形的性质与判定,相似三角形的性质与判定,旋转的性质,轴对称的
性质,第(2) 题关键在证明全等三角形,第(2) 题关键确定M、N的位置.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布 ① ②
日期:2020/9/4 12:32:57;用户:18366185883;邮箱:18366185883;学号:22597006
第20页(共20页)