文档内容
三明市 2024 年普通高中高三毕业班质量检测
数 学 试 题
(本试卷总分150分, 考试时间120分钟。)
注意事项:
1. 答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2. 回答选择题时,选出每题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。 如需改动,
用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无
效。
3. 考试结束后,将答题卡交回。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题
目要求的.
1.已知直线y=-x+2与圆 x²+ y²=4相交于M,N两点,则|MN|=
A.❑√2 B.2 C.2❑√2 D.4
2. 已知a,b,c分别为ΔABC三个内角A,B,C的对边, a=3,b=❑√37,c=7,则A+C的值为
π π 2π 5π
A. B. C. D.
6 3 3 6
1
3.随机变量ξ~ N(μ,σ²),函数 f (x)=x²−4x+ξ没有零点的概率是 ,则μ的值为
2
A. 1 B.2 C.3 D.4
( 2) 2 ( 1) 2 1
4.若 a= − 3,b= − 3,c=log ,则
3 3 2 3
3
A. c>a>b B. c>b>a C. a>b>c D. b>c>a
5.各种不同的进制在生活中随处可见,计算机使用的是二进制,数学运算一般使用的是十进制,任
何 进 制 数 均 可 转 换 为 十 进 制 数 , 如 八 进 制 数 ( 3750 ) 转 换 为 十 进 制 数 的 算 法 为
8
77⋯7
3×8³+7×8²+5×8¹+0×8⁰ =2024.若将八进制数 转换为十进制数,则转换后的数的末位数字
6个7
是
A.3 B.4 C.5 D.6
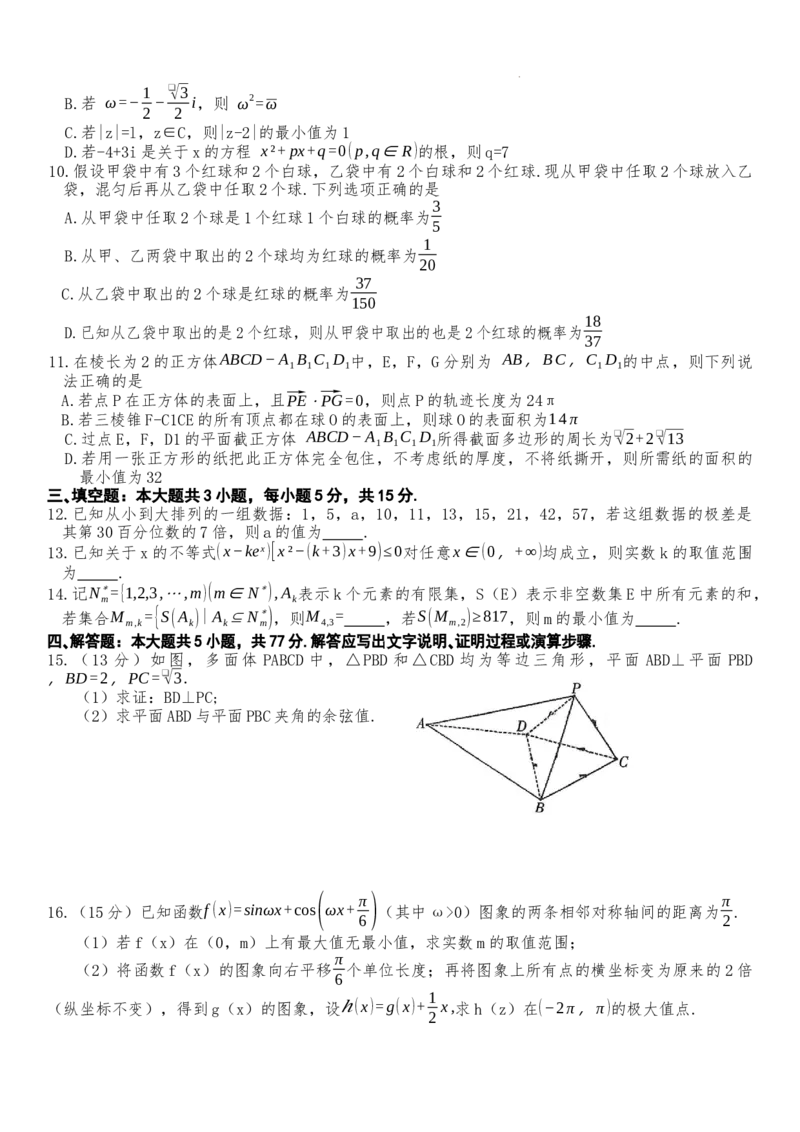
6.函数 f (x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示,其中 A,B两点为图象与x轴的交点,
C为图象的最高点,且△ABC是等腰直角三角形,若 ⃗OB=−3⃗OA, 则
向量 ⃗AO在向量 ⃗AC上的投影向量的坐标为
( 1 1 ) ( 1 1 )
A. − , − B. ,
4 4 4 4
( 1 1 ) ( 1 1 )
C. − , − D. ,
2 2 2 2
7.已知抛物线x²=2p y(p>0)的焦点为F,第一象限的两点A,B在抛物线上,且满足|AF|-|BF|=3,|
AB|=3 ❑√2若线段AB中点的横坐标为3,则p的值为
A.2 B.3 C.4 D.5
8.已知函数f (x)=eˣ⁻¹−e¹⁻ˣ+x³−3x²+3x,若实数x,y满足f (3x²)+f (2y²−4)=2,则x+y的最大
值为
❑√5 ❑√30
A. 1 B. C.❑√5 D.
2 3
二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全
部选对的得6分,部分选对的得部分分,有选错的得0分.
9.i是虚数单位,下列说法正确的是
A.i2024=−1
学科网(北京)股份有限公司1 ❑√3
B.若 ω=− − i,则 ω2=ω
2 2
C.若|z|=l,z∈C,则|z-2|的最小值为1
D.若-4+3i是关于x的方程 x²+px+q=0(p,q∈R)的根,则q=7
10.假设甲袋中有3个红球和2个白球,乙袋中有2个白球和2个红球.现从甲袋中任取2个球放入乙
袋,混匀后再从乙袋中任取2个球.下列选项正确的是
3
A.从甲袋中任取2个球是1个红球1个白球的概率为
5
1
B.从甲、乙两袋中取出的2个球均为红球的概率为
20
37
C.从乙袋中取出的2个球是红球的概率为
150
18
D.已知从乙袋中取出的是2个红球,则从甲袋中取出的也是2个红球的概率为
37
11.在棱长为2的正方体ABCD−A B C D 中,E,F,G分别为 AB,BC,C D 的中点,则下列说
1 1 1 1 1 1
法正确的是
A.若点P在正方体的表面上,且⃗PE⋅⃗PG=0,则点P的轨迹长度为24π
B.若三棱锥F-C1CE的所有顶点都在球O的表面上,则球O的表面积为14π
C.过点E,F,D1的平面截正方体 ABCD−A B C D 所得截面多边形的周长为❑√2+2❑√13
1 1 1 1
D.若用一张正方形的纸把此正方体完全包住,不考虑纸的厚度,不将纸撕开,则所需纸的面积的
最小值为32
三、填空题:本大题共3小题,每小题5分,共15分.
12.已知从小到大排列的一组数据:1,5,a,10,11,13,15,21,42,57,若这组数据的极差是
其第30百分位数的7倍,则a的值为 .
13.已知关于x的不等式(x−keˣ)[x²−(k+3)x+9)≤0对任意x∈(0,+∞)均成立,则实数k的取值范围
为 .
14.记N∗={1,2,3,⋯,m)(m∈N∗),A 表示k个元素的有限集,S(E)表示非空数集E中所有元素的和,
m k
若集合M ={S(A )|A ⊆N∗),则M = ,若S(M )≥817,则m的最小值为 .
m,k k k m 4,3 m,2
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13 分)如图,多面体 PABCD 中,△PBD 和△CBD 均为等边三角形,平面 ABD⊥平面 PBD
,BD=2,PC=❑√3.
(1)求证:BD⊥PC;
(2)求平面ABD与平面PBC夹角的余弦值.
( π) π
16.(15分)已知函数f (x)=sinωx+cos ωx+ (其中ω>0)图象的两条相邻对称轴间的距离为 .
6 2
(1)若f(x)在(0,m)上有最大值无最小值,求实数m的取值范围;
π
(2)将函数f(x)的图象向右平移 个单位长度;再将图象上所有点的横坐标变为原来的 2倍
6
1
(纵坐标不变),得到g(x)的图象,设ℎ(x)=g(x)+ x,求h(z)在(−2π,π)的极大值点.
2
学科网(北京)股份有限公司17.(15分)某校开设劳动教育课程,为了有效推动课程实施,学校开展劳动课程知识问答竞赛,
1 1 1
现有家政、园艺、民族工艺三类问题海量题库,其中家政类占 ,园艺类占 民族工艺类占 .根据
4 4 2
2 2 4
以往答题经验,选手甲答对家政类、园艺类、民族工艺类题目的概率分别为 , , ,选手乙答对这
5 5 5
1
三类题目的概率均为 .
2
(1)求随机任选1题,甲答对的概率;
(2)现进行甲、乙双人对抗赛,规则如下:两位选手进行三轮答题比赛,每轮只出 1道题目,
比赛时两位选手同时回答这道题,若一人答对且另一人答错,则答对者得1分,答错者得-1分,
若两人都答对或都答错,则两人均得0分,累计得分为正者将获得奖品,且两位选手答对与否互
不影响,每次答题的结果也互不影响,求甲获得奖品的概率.
18.(17分)已知数列{aₙ }满足a ⋅a ⋯a ⋅a =(❑√2)
n2+a
,n∈N∗.
1 2 o−1 n
(1)求数列{aₙ }的通项公式;
(2)设数列{aₙ }的前n项和为Sₙ ,若不等式(−1) ntS −14≤S 2对任意的n∈N∗恒成立,求实数t
n n
的取值范围;
1 b −b b −b b −b
(3) 记 b = ,求证: 1 2+ 2 3+⋯+ a n+1<❑√2(n∈N∗).
n log a ❑√b ❑√b ❑√b
2 n 1 2 a
学科网(北京)股份有限公司19. ( 17 分 ) 已 知 平 面 直 角 坐 标 系 xoy 中 , 有 真 命 题 : 函 数
n
y=mx+ (m≥0,n>0)的图象是双曲线,其渐近线分别为直线 y=mx和y轴.例
x
4
如双曲线 y= 的渐近线分别为 x轴和y轴,可将其图象绕原点 O顺时针旋转
x
π
得到双曲线 x²−y²=8的图象.
4
1
(1)求双曲线 y= 的离心率:
x
(2)已知曲线 E:x²−y²=2,过E上一点P作切线分别交两条渐近线于A,B
两点,试探究 △AOB面积是否为定值,若是,则求出该定值;若不是,则说明
理由;
❑√3 ❑√3
(3)已知函数 y= x+ 的图象为 Γ,直线 l:x+❑√3 y−3=0,过
3 2x
的直线与Γ在第一象限交于 M,N两点,过M,N作l的垂线,垂足分
F(1,❑√3)
别为C,D,直线MD,NC交于点H,求△MNH面积的最小值.
学科网(北京)股份有限公司