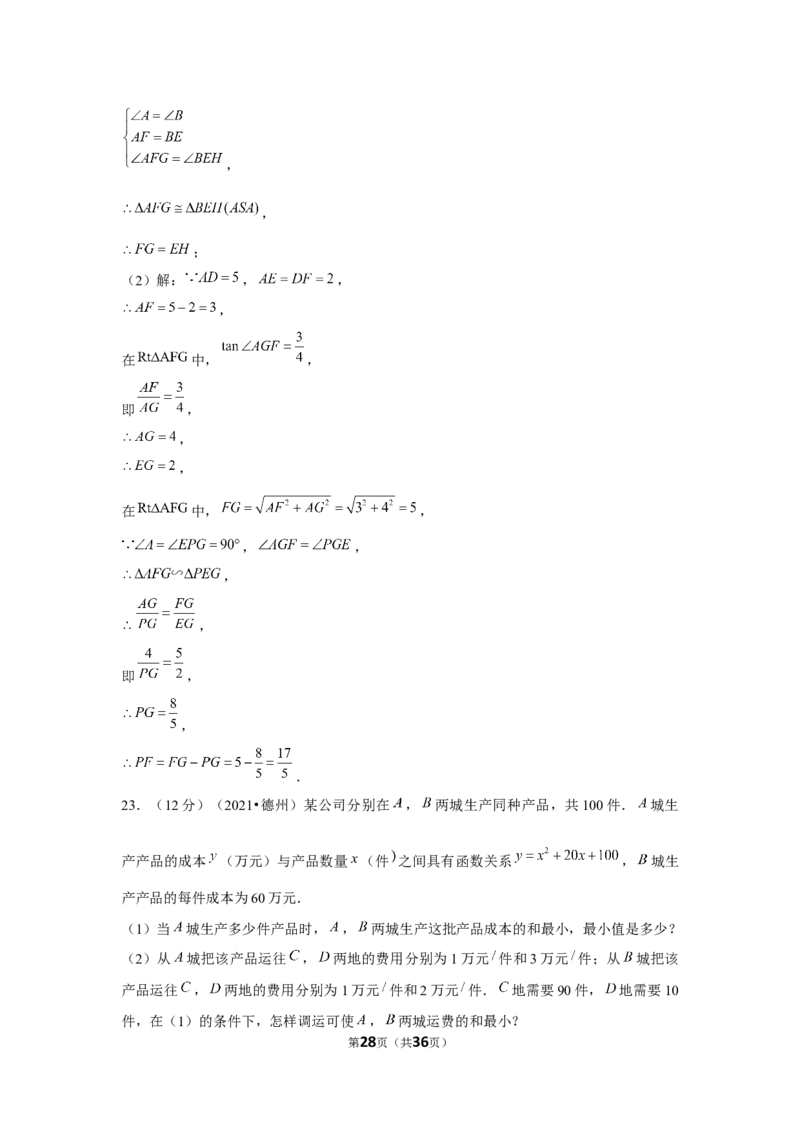文档内容
2021年山东省德州市中考数学试卷
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正
确的选项选出来,每小题选对得4分,选错、不选或选出的答案超过一个均记分.
1.(4分)(2021•德州) 的相反数是
A. B.3 C. D.
2.(4分)(2021•德州)据国家统计局公布,我国第七次全国人口普查结果约为14.12亿
人,14.12亿用科学记数法表示为
A. B. C. D.
3.(4分)(2021•德州)下列运算正确的是
A. B.
C. D.
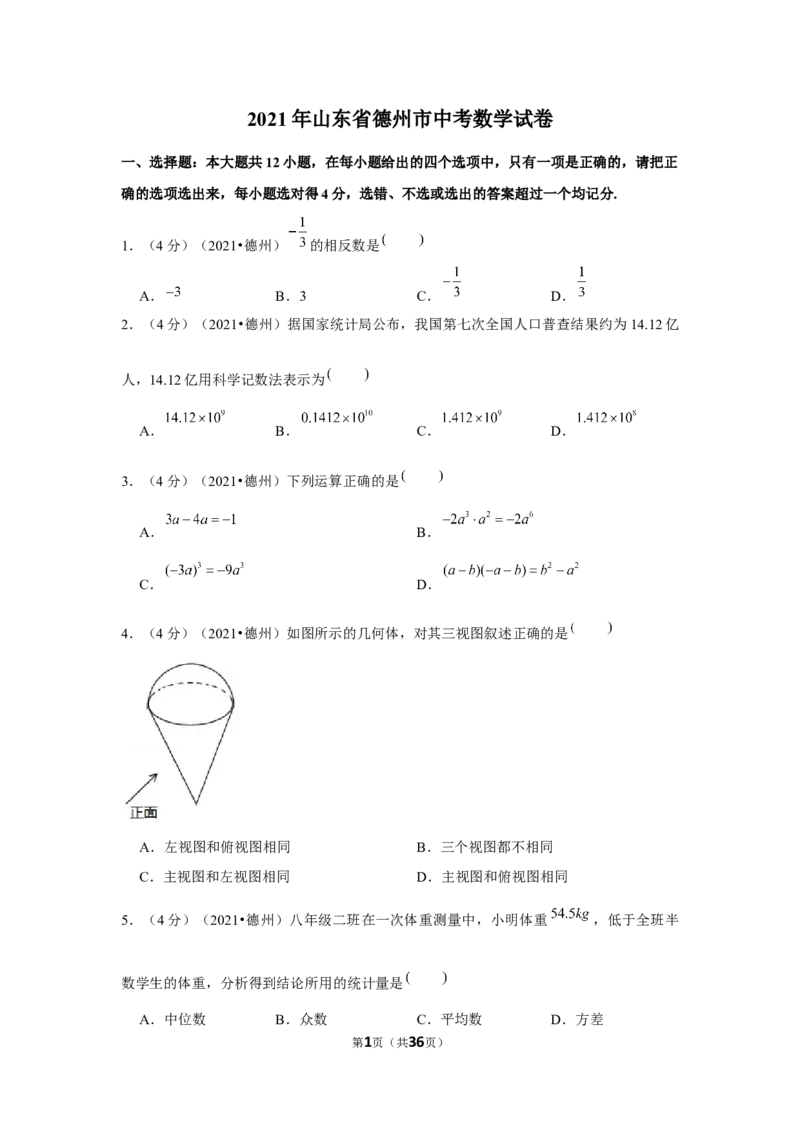
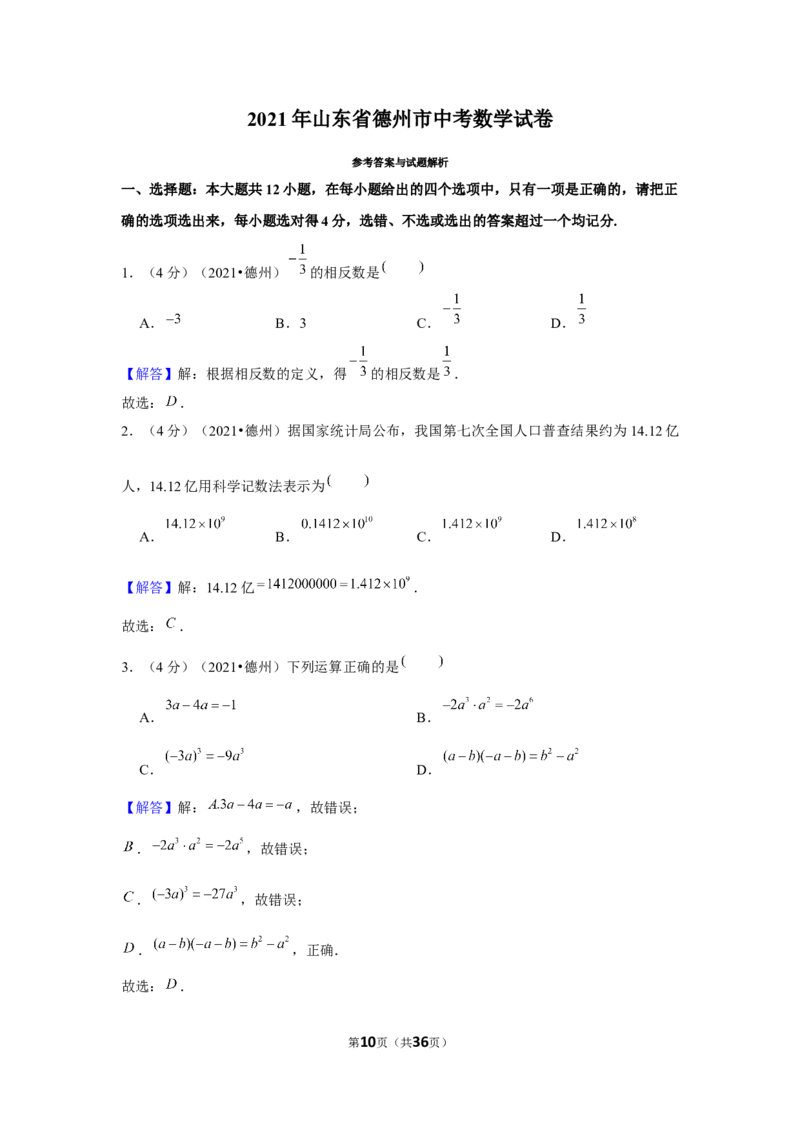
4.(4分)(2021•德州)如图所示的几何体,对其三视图叙述正确的是
A.左视图和俯视图相同 B.三个视图都不相同
C.主视图和左视图相同 D.主视图和俯视图相同
5.(4分)(2021•德州)八年级二班在一次体重测量中,小明体重 ,低于全班半
数学生的体重,分析得到结论所用的统计量是
A.中位数 B.众数 C.平均数 D.方差
第1页(共36页)6.(4分)(2021•德州)下列选项中能使 成为菱形的是
A. B. C. D.
7.(4分)(2021•德州)为响应“绿色出行”的号召,小王上班由自驾车改为乘坐公交
车.已知小王家距上班地点 ,他乘公交车平均每小时行驶的路程比他自驾车平均每小
时行驶的路程多 .他从家出发到上班地点,乘公交车所用的时间是自驾车所用时间的
.小王乘公交车上班平均每小时行驶
A. B. C. D.
8.(4分)(2021•德州)如图,在矩形 中, , ,以点 为圆心,
长为半径画弧交 于点 ,连接 ,则阴影部分的面积为
A. B. C. D.
9.(4分)(2021•德州)已知点 , , , , , 都在反比例函数
是常数)的图象上,且 ,则 , , 的大小关系为
A. B. C. D.
10.(4分)(2021•德州)某商场准备改善原有楼梯的安全性能,把坡角由 减至 ,
已知原楼梯长为5米,调整后的楼梯会加长 (参考数据: , ,
.
第2页(共36页)A.6米 B.3米 C.2米 D.1米
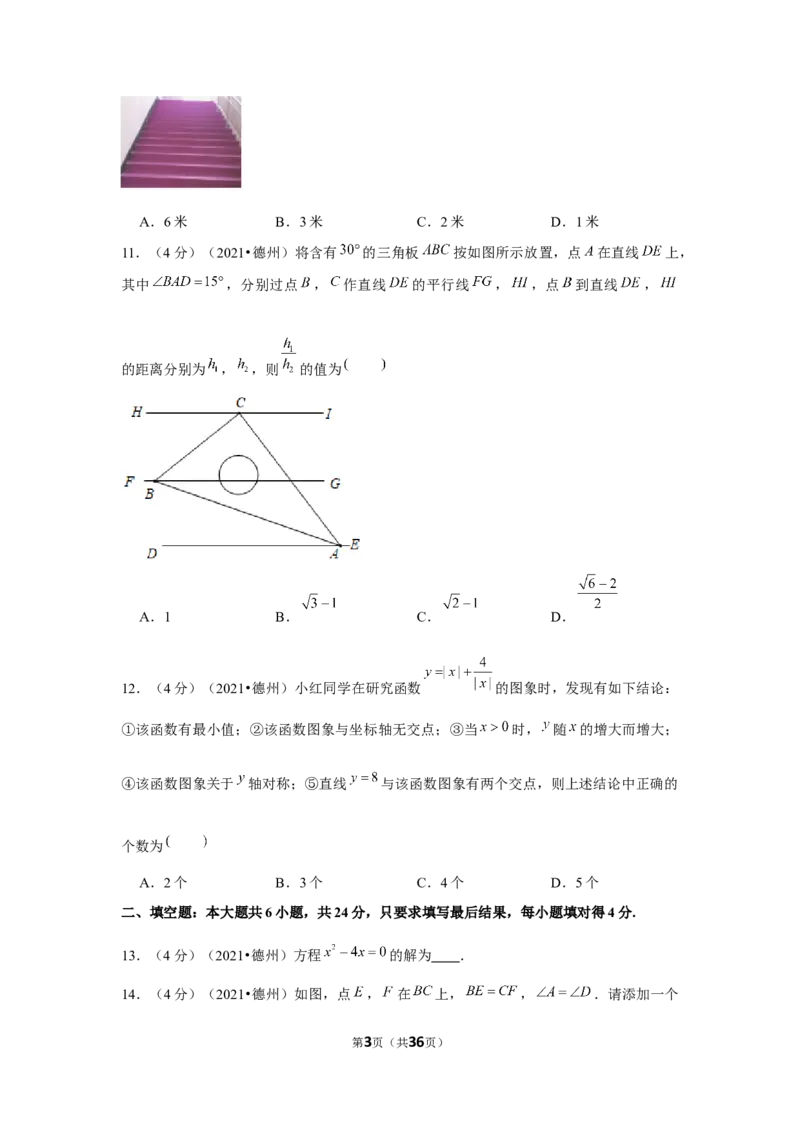
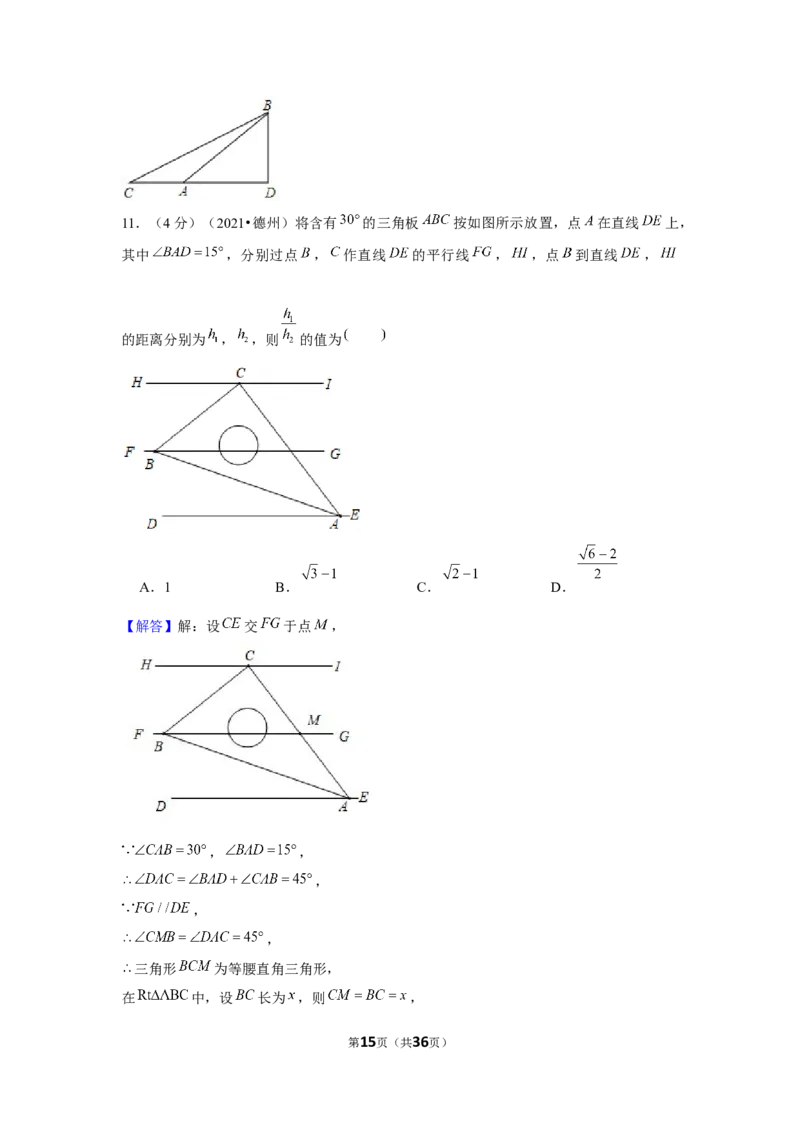
11.(4分)(2021•德州)将含有 的三角板 按如图所示放置,点 在直线 上,
其中 ,分别过点 , 作直线 的平行线 , ,点 到直线 ,
的距离分别为 , ,则 的值为
A.1 B. C. D.
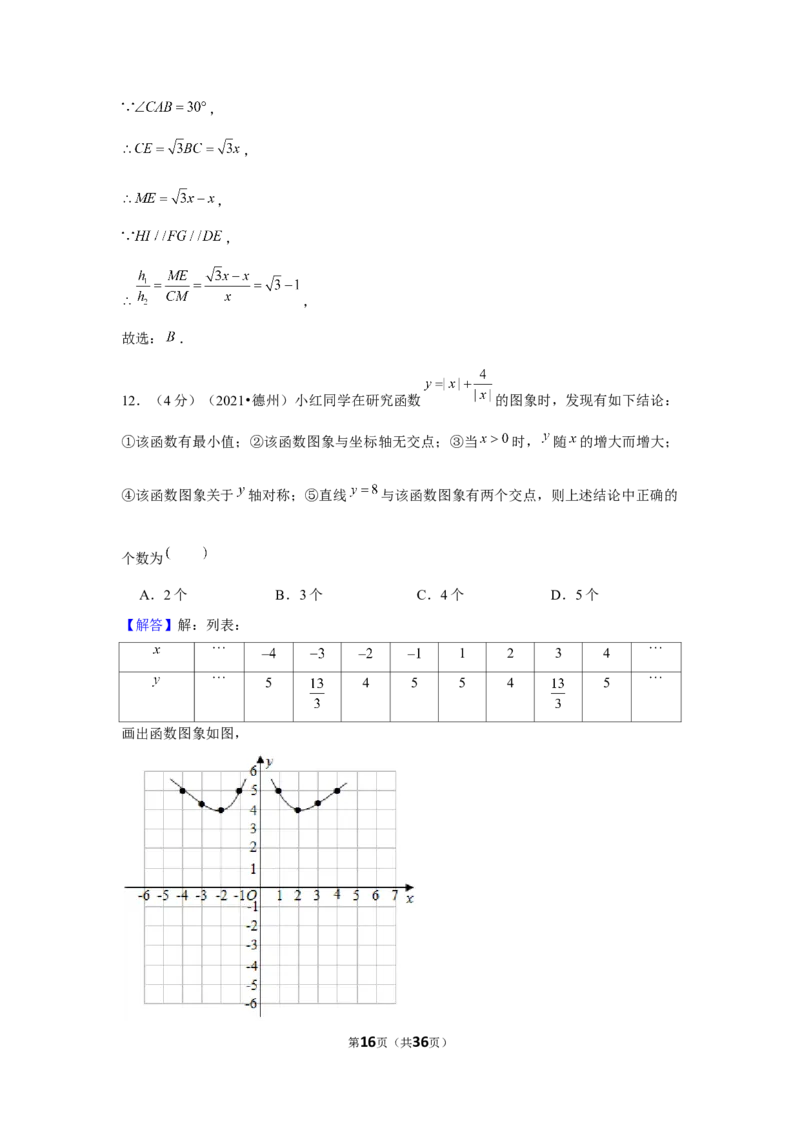
12.(4分)(2021•德州)小红同学在研究函数 的图象时,发现有如下结论:
①该函数有最小值;②该函数图象与坐标轴无交点;③当 时, 随 的增大而增大;
④该函数图象关于 轴对称;⑤直线 与该函数图象有两个交点,则上述结论中正确的
个数为
A.2个 B.3个 C.4个 D.5个
二、填空题:本大题共6小题,共24分,只要求填写最后结果,每小题填对得4分.
13.(4分)(2021•德州)方程 的解为 .
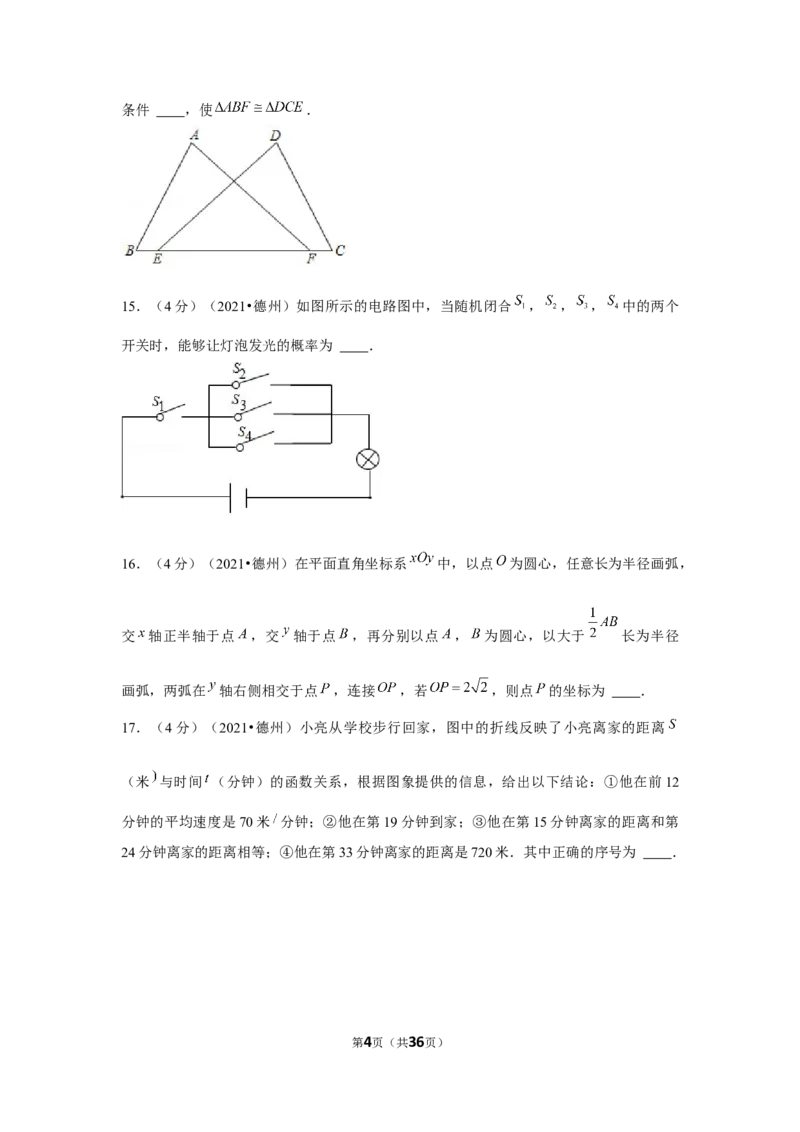
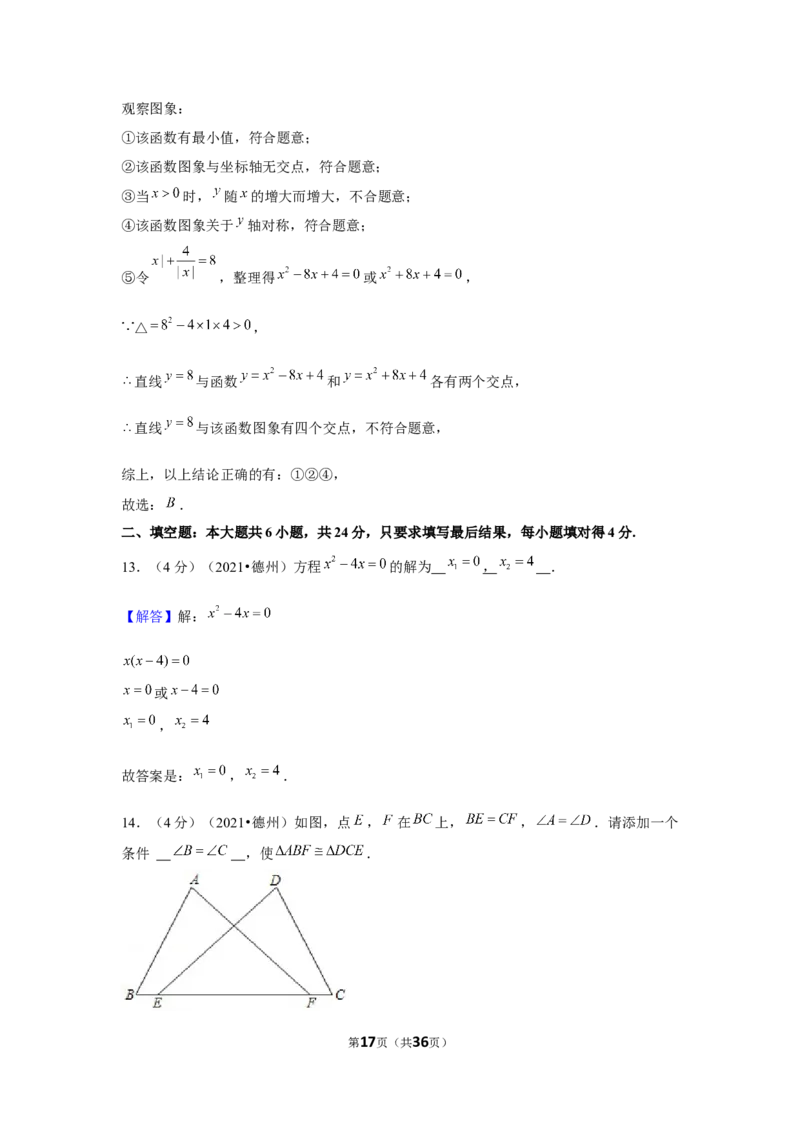
14.(4分)(2021•德州)如图,点 , 在 上, , .请添加一个
第3页(共36页)条件 ,使 .
15.(4分)(2021•德州)如图所示的电路图中,当随机闭合 , , , 中的两个
开关时,能够让灯泡发光的概率为 .
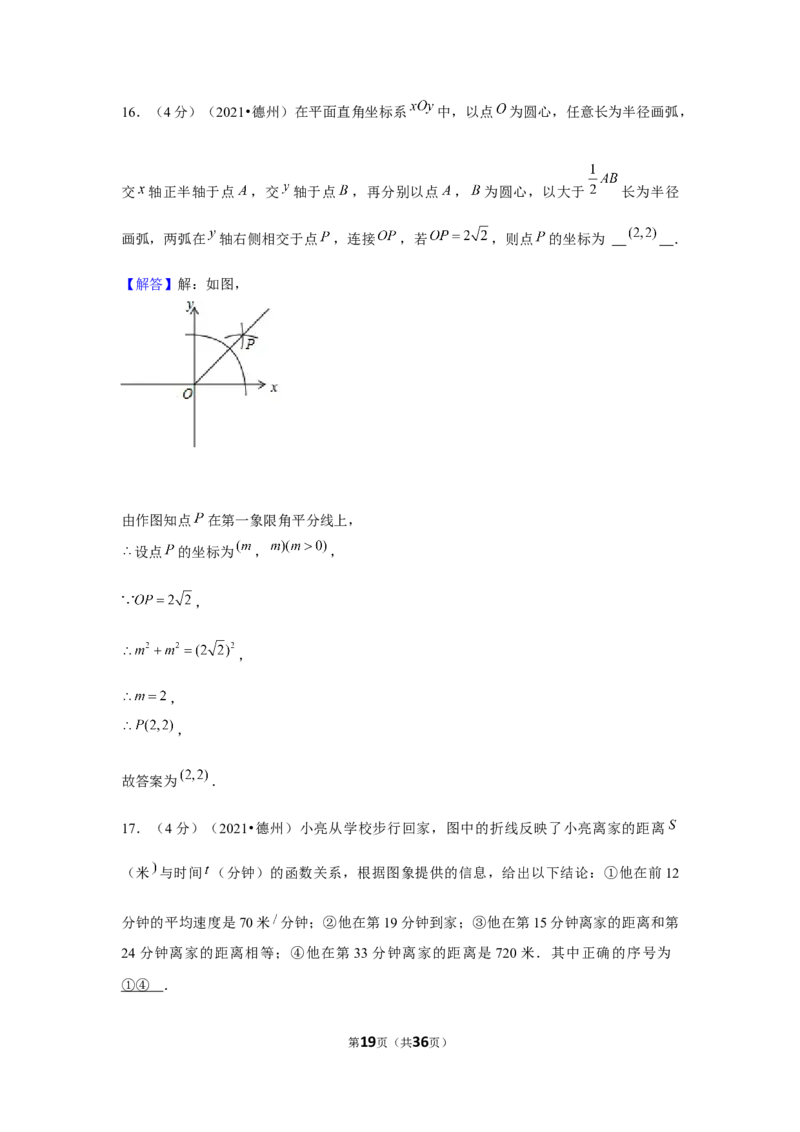
16.(4分)(2021•德州)在平面直角坐标系 中,以点 为圆心,任意长为半径画弧,
交 轴正半轴于点 ,交 轴于点 ,再分别以点 , 为圆心,以大于 长为半径
画弧,两弧在 轴右侧相交于点 ,连接 ,若 ,则点 的坐标为 .
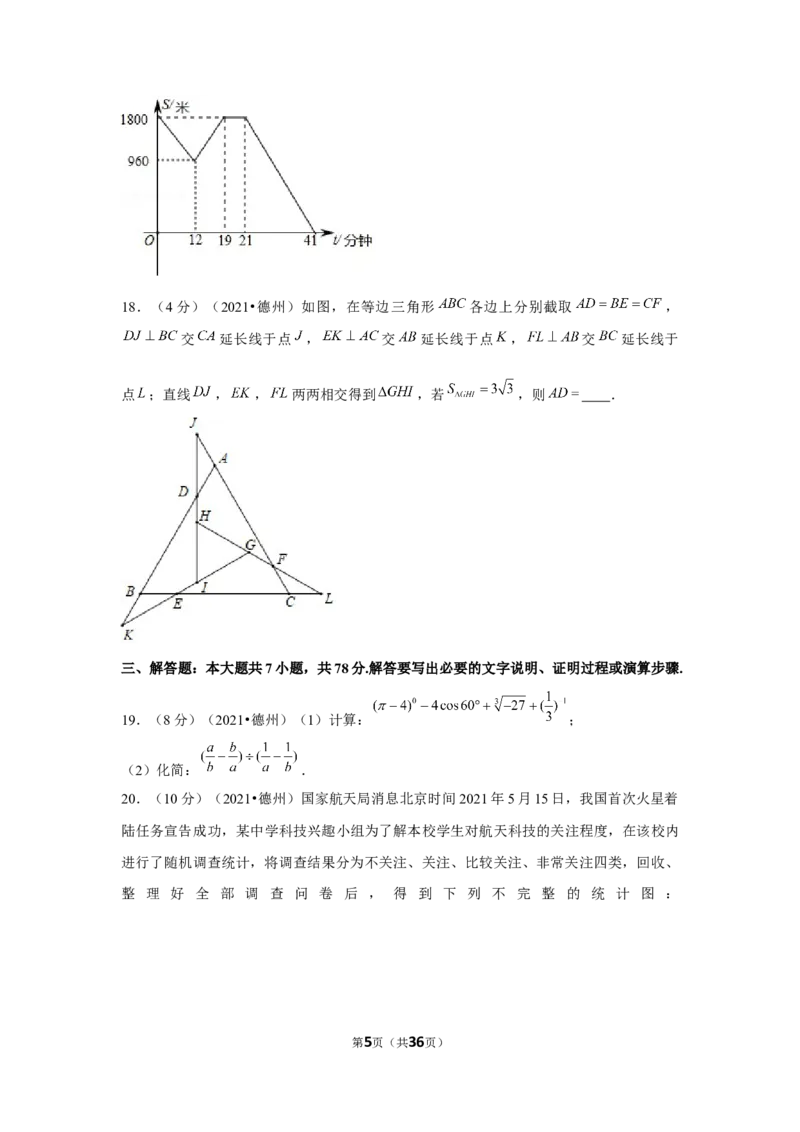
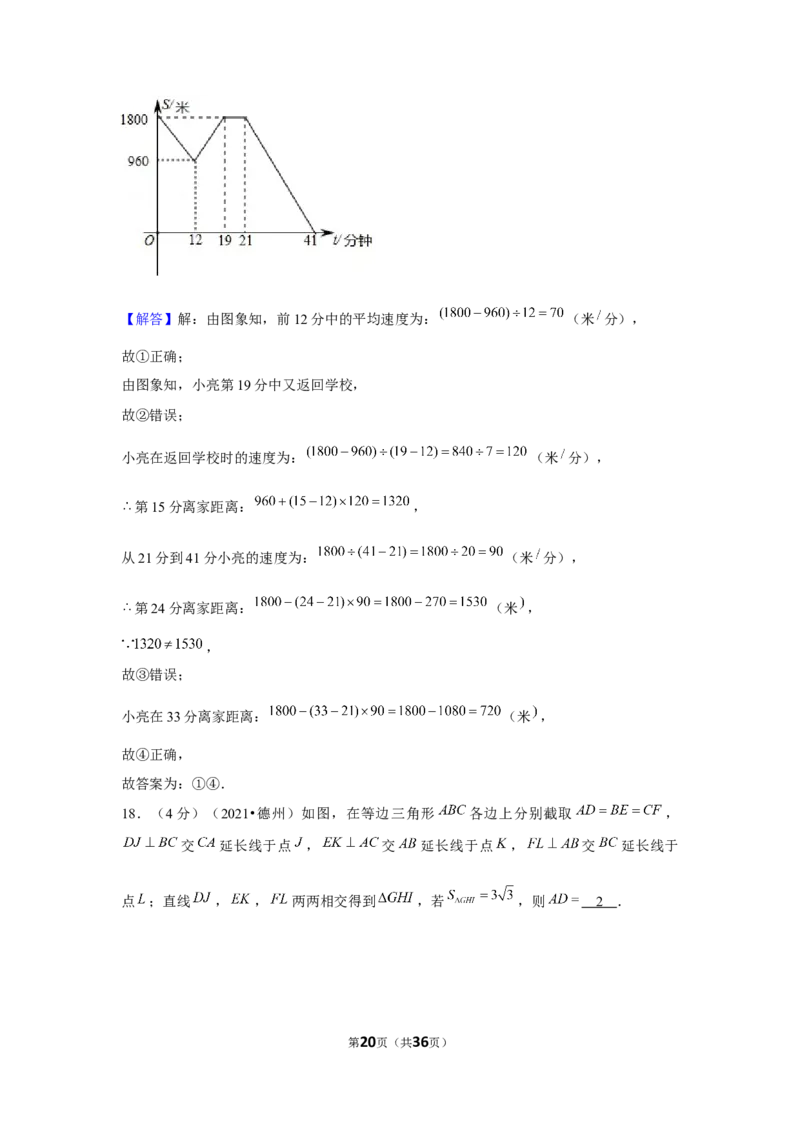
17.(4分)(2021•德州)小亮从学校步行回家,图中的折线反映了小亮离家的距离
(米 与时间 (分钟)的函数关系,根据图象提供的信息,给出以下结论:①他在前12
分钟的平均速度是70米 分钟;②他在第19分钟到家;③他在第15分钟离家的距离和第
24分钟离家的距离相等;④他在第33分钟离家的距离是720米.其中正确的序号为 .
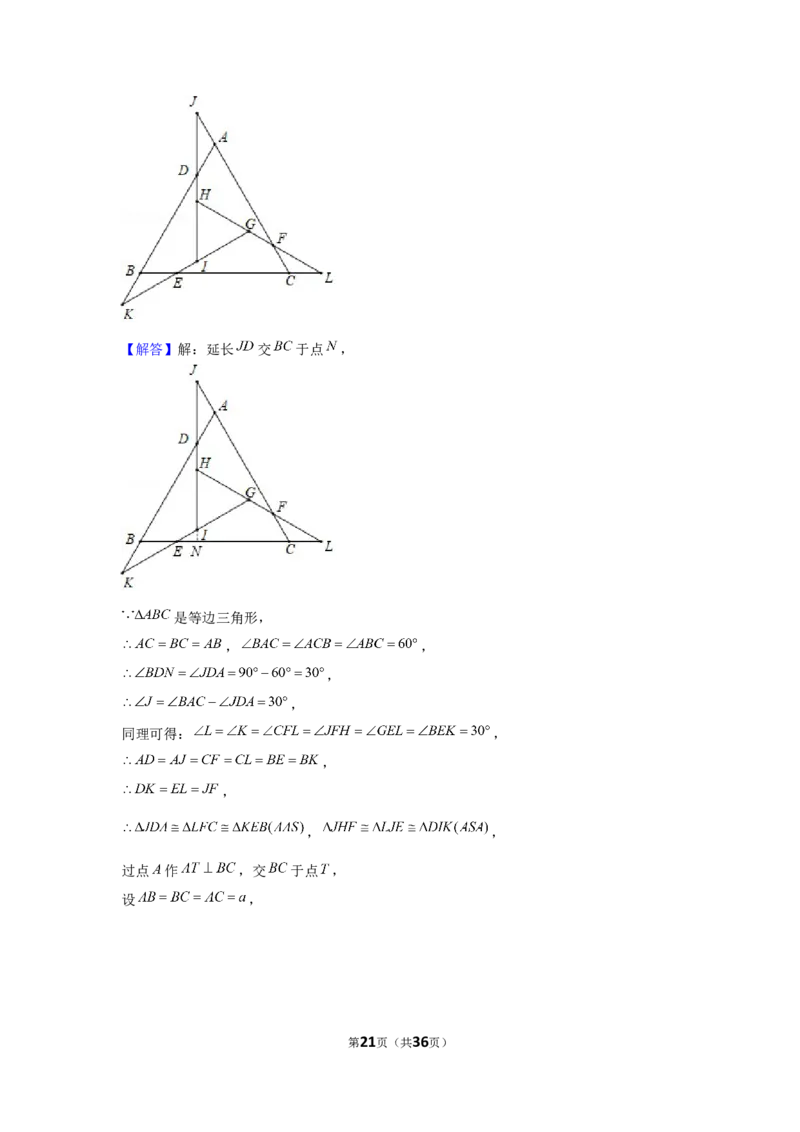
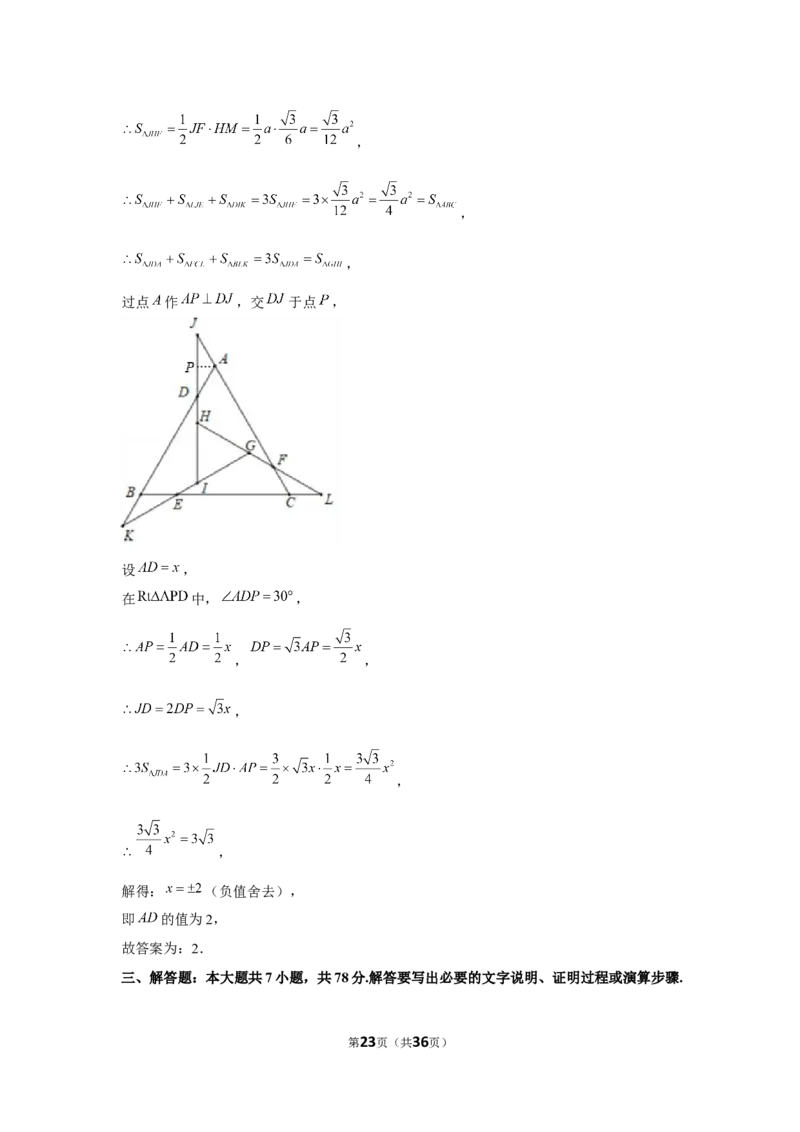
第4页(共36页)18.(4分)(2021•德州)如图,在等边三角形 各边上分别截取 ,
交 延长线于点 , 交 延长线于点 , 交 延长线于
点 ;直线 , , 两两相交得到 ,若 ,则 .
三、解答题:本大题共7小题,共78分.解答要写出必要的文字说明、证明过程或演算步骤.
19.(8分)(2021•德州)(1)计算: ;
(2)化简: .
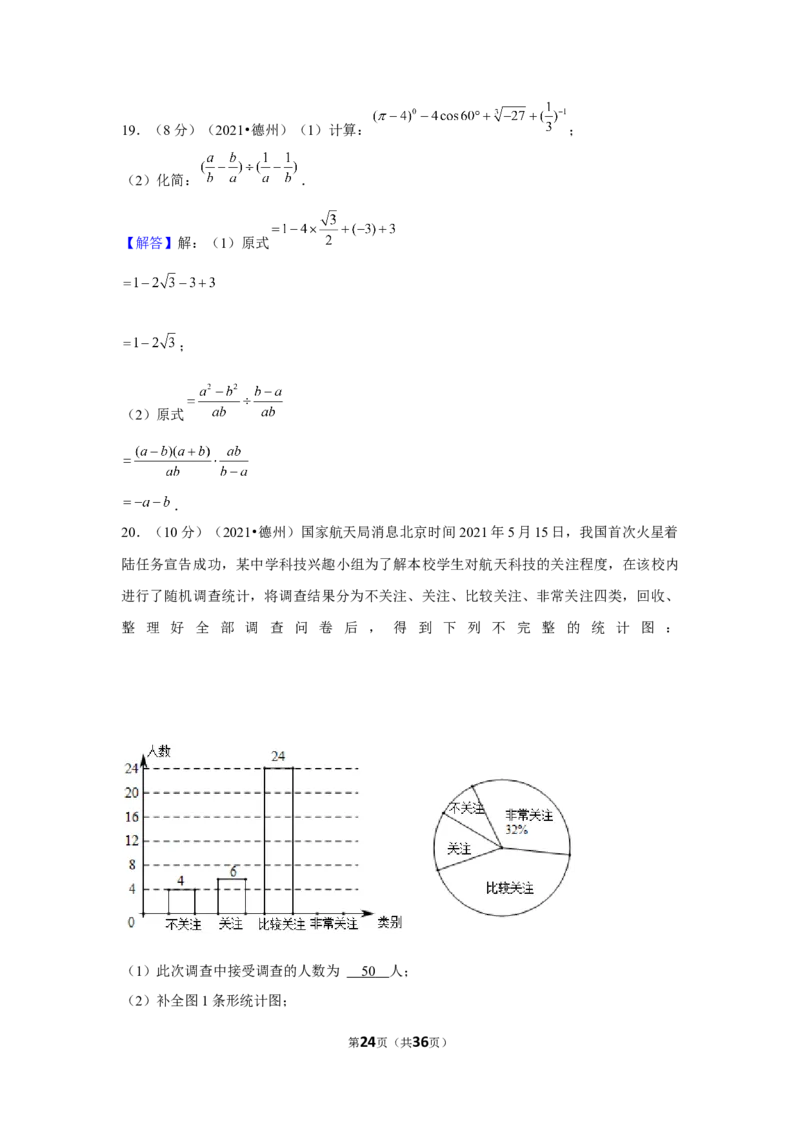
20.(10分)(2021•德州)国家航天局消息北京时间2021年5月15日,我国首次火星着
陆任务宣告成功,某中学科技兴趣小组为了解本校学生对航天科技的关注程度,在该校内
进行了随机调查统计,将调查结果分为不关注、关注、比较关注、非常关注四类,回收、
整 理 好 全 部 调 查 问 卷 后 , 得 到 下 列 不 完 整 的 统 计 图 :
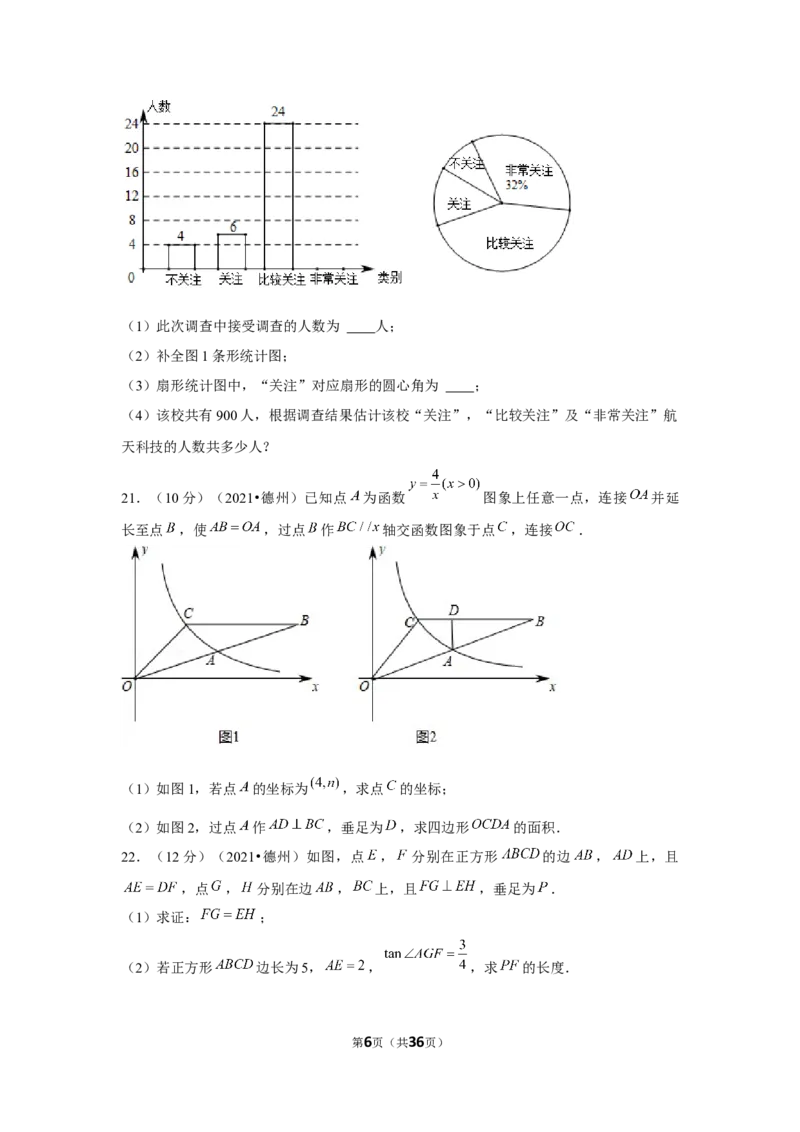
第5页(共36页)(1)此次调查中接受调查的人数为 人;
(2)补全图1条形统计图;
(3)扇形统计图中,“关注”对应扇形的圆心角为 ;
(4)该校共有900人,根据调查结果估计该校“关注”,“比较关注”及“非常关注”航
天科技的人数共多少人?
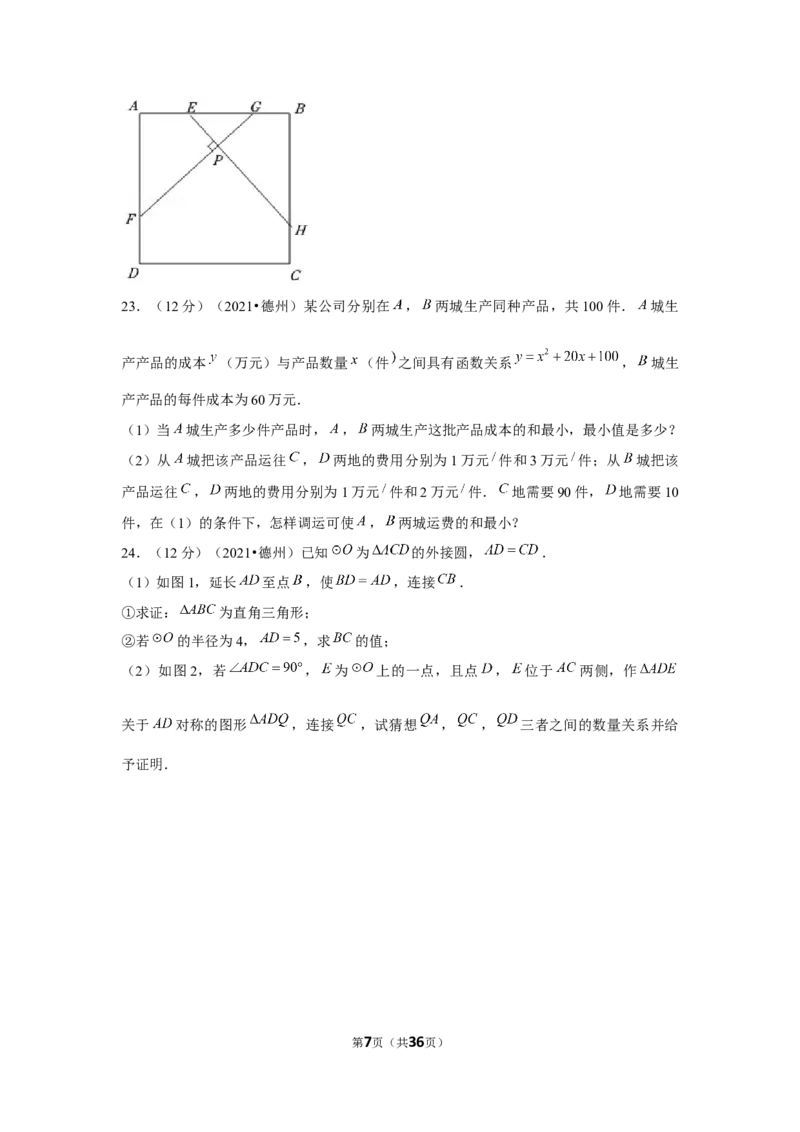
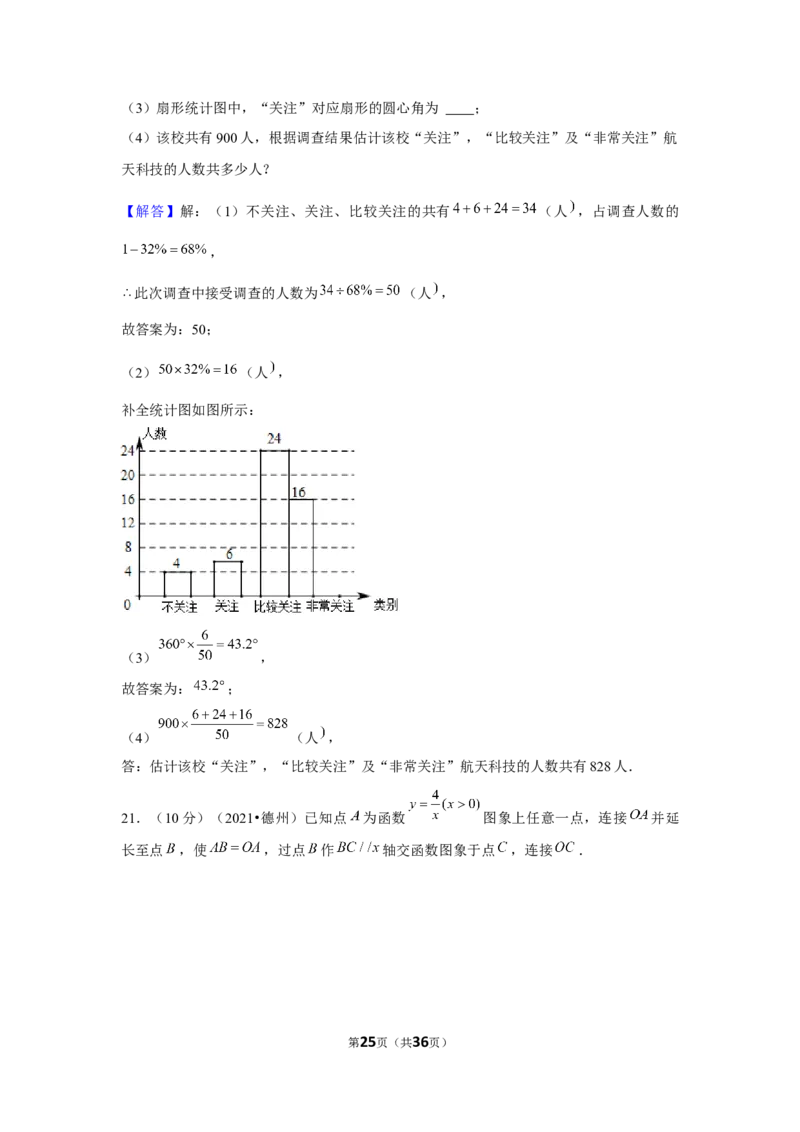
21.(10分)(2021•德州)已知点 为函数 图象上任意一点,连接 并延
长至点 ,使 ,过点 作 轴交函数图象于点 ,连接 .
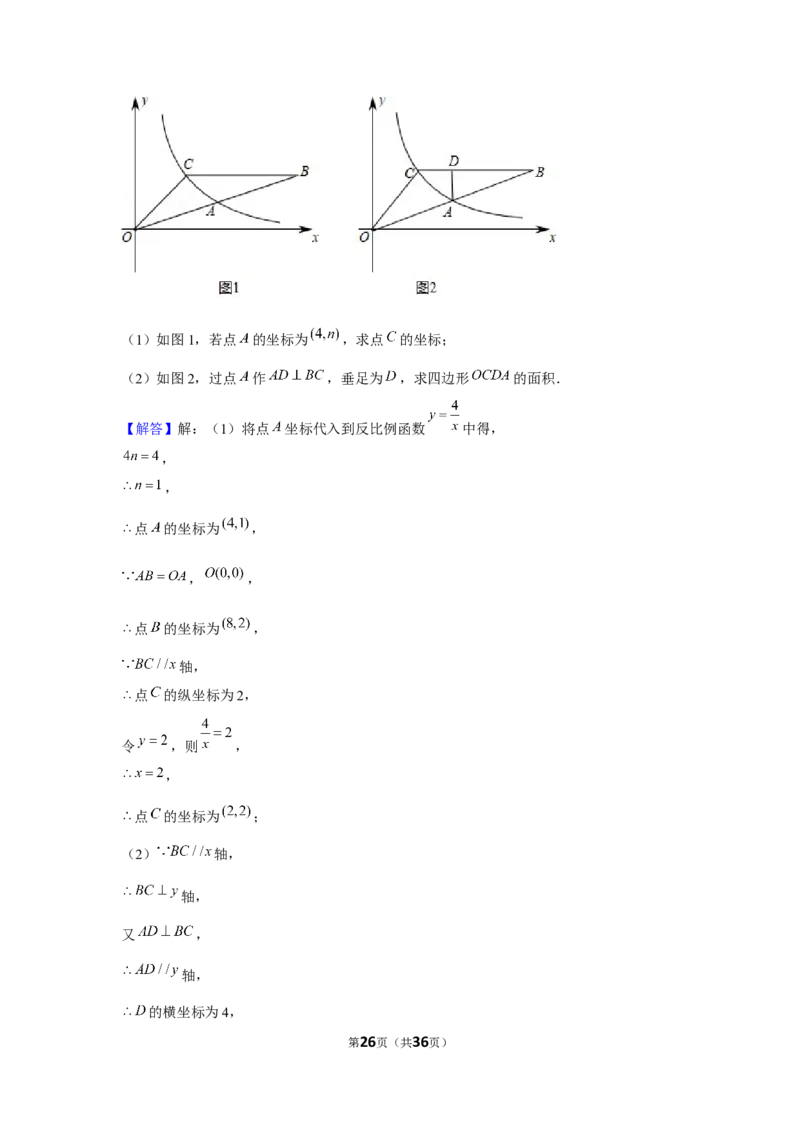
(1)如图1,若点 的坐标为 ,求点 的坐标;
(2)如图2,过点 作 ,垂足为 ,求四边形 的面积.
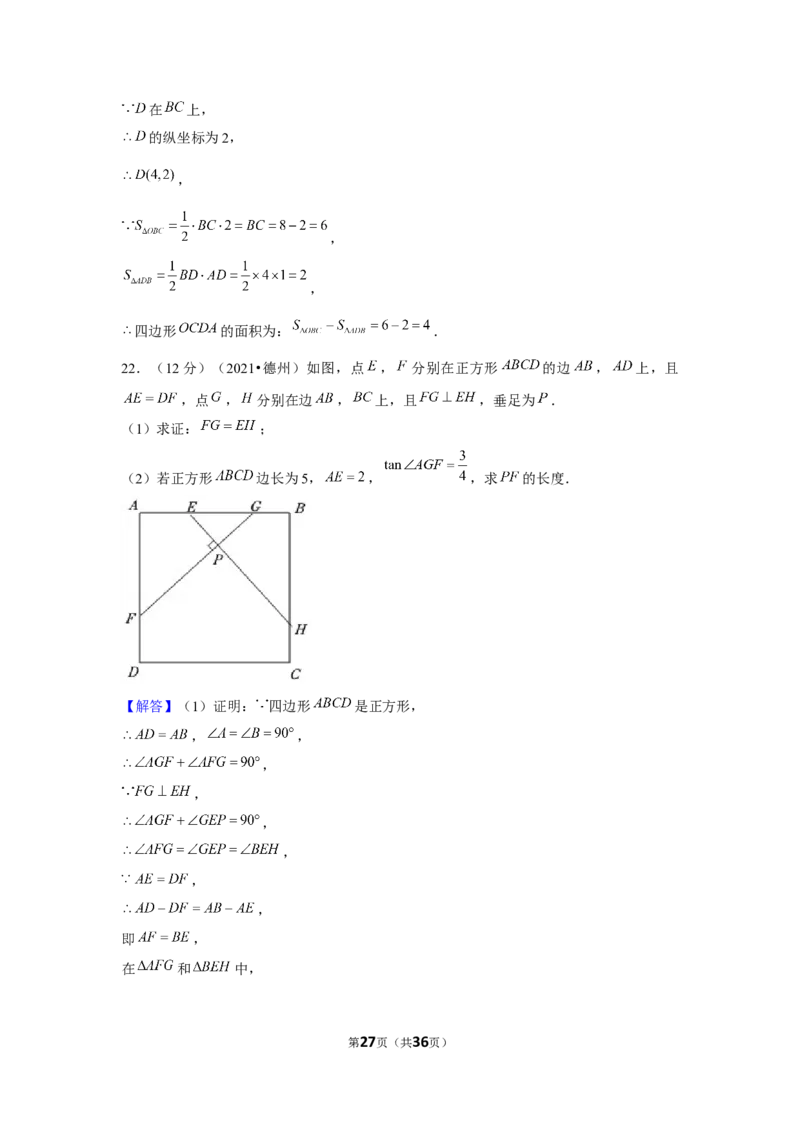
22.(12分)(2021•德州)如图,点 , 分别在正方形 的边 , 上,且
,点 , 分别在边 , 上,且 ,垂足为 .
(1)求证: ;
(2)若正方形 边长为5, , ,求 的长度.
第6页(共36页)23.(12分)(2021•德州)某公司分别在 , 两城生产同种产品,共100件. 城生
产产品的成本 (万元)与产品数量 (件 之间具有函数关系 , 城生
产产品的每件成本为60万元.
(1)当 城生产多少件产品时, , 两城生产这批产品成本的和最小,最小值是多少?
(2)从 城把该产品运往 , 两地的费用分别为1万元 件和3万元 件;从 城把该
产品运往 , 两地的费用分别为1万元 件和2万元 件. 地需要90件, 地需要10
件,在(1)的条件下,怎样调运可使 , 两城运费的和最小?
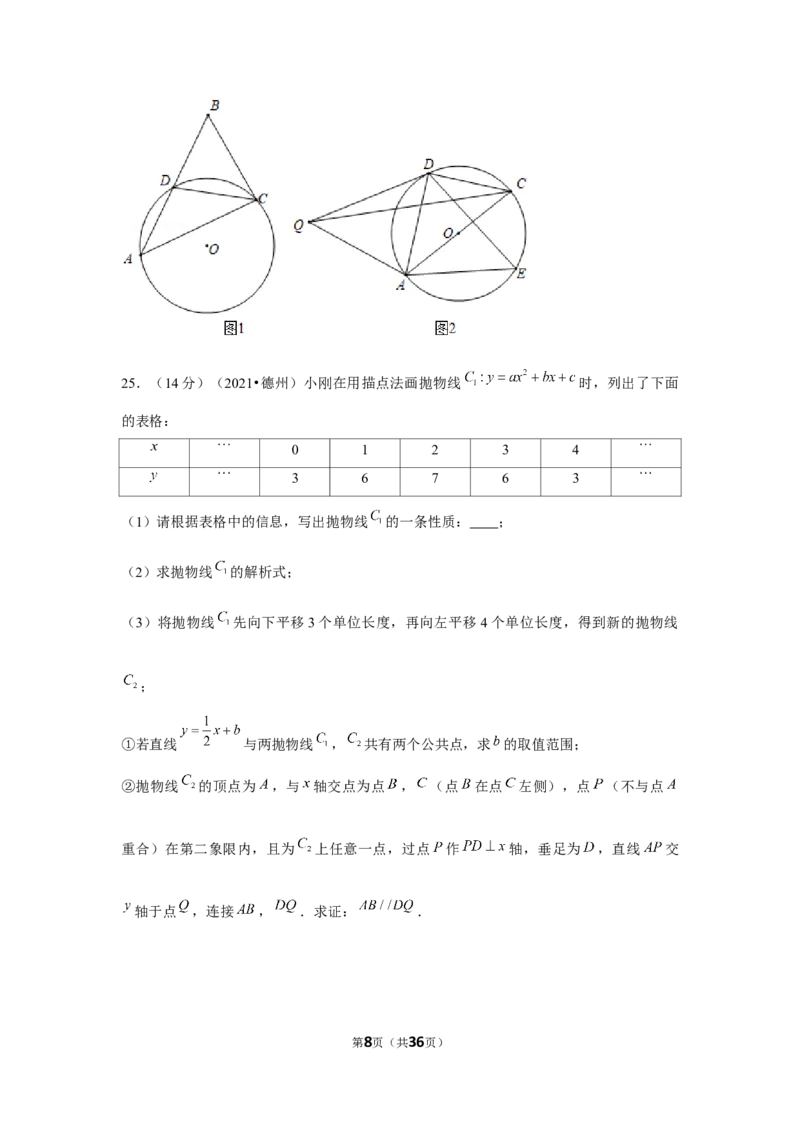
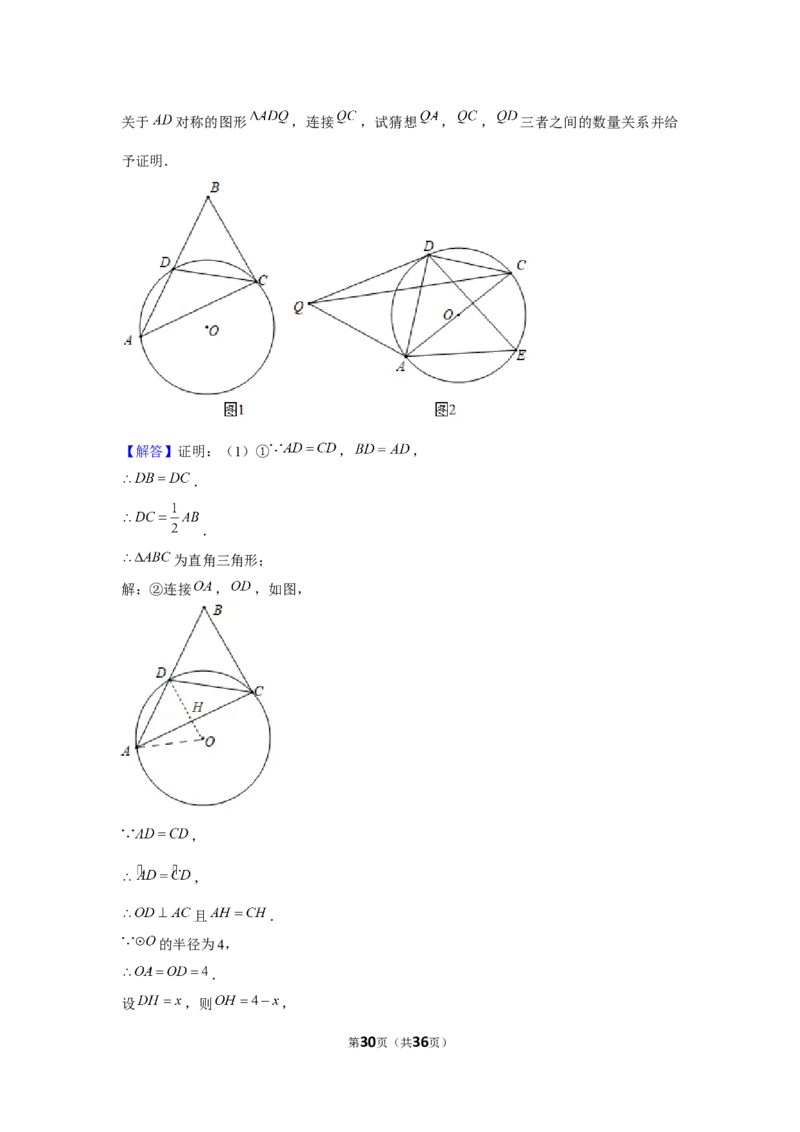
24.(12分)(2021•德州)已知 为 的外接圆, .
(1)如图1,延长 至点 ,使 ,连接 .
①求证: 为直角三角形;
②若 的半径为4, ,求 的值;
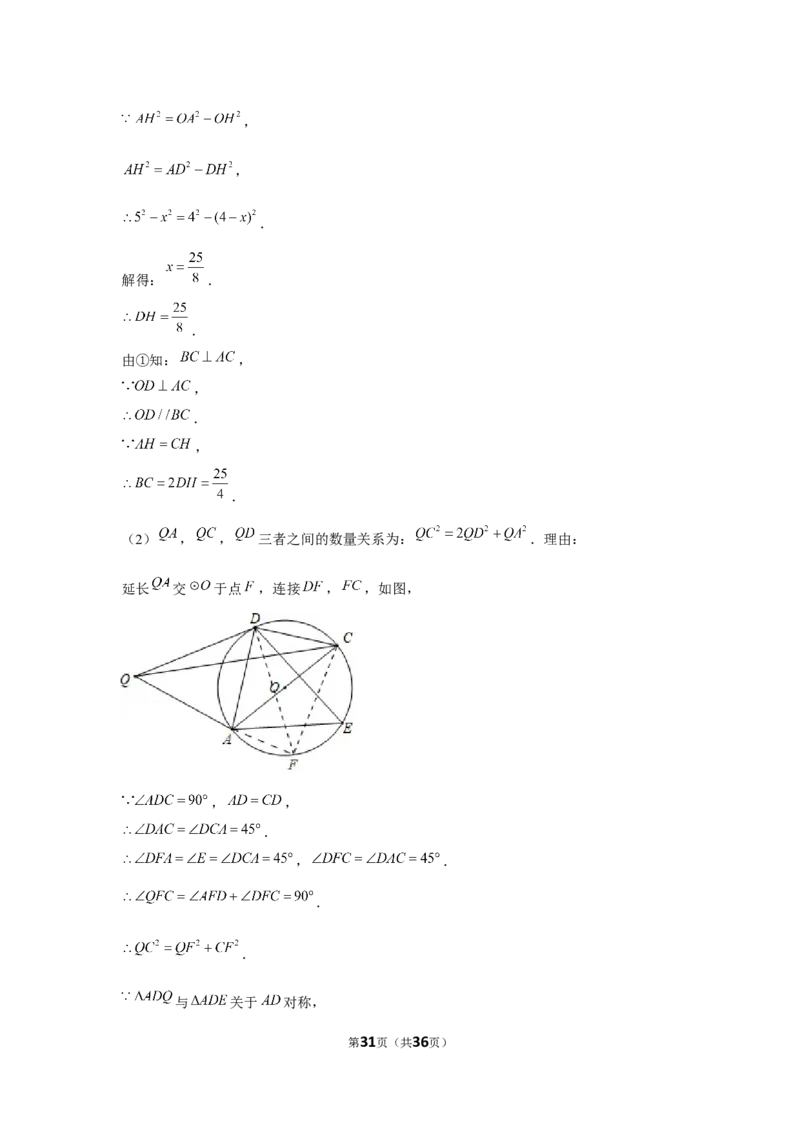
(2)如图2,若 , 为 上的一点,且点 , 位于 两侧,作
关于 对称的图形 ,连接 ,试猜想 , , 三者之间的数量关系并给
予证明.
第7页(共36页)25.(14分)(2021•德州)小刚在用描点法画抛物线 时,列出了下面
的表格:
0 1 2 3 4
3 6 7 6 3
(1)请根据表格中的信息,写出抛物线 的一条性质: ;
(2)求抛物线 的解析式;
(3)将抛物线 先向下平移3个单位长度,再向左平移4个单位长度,得到新的抛物线
;
①若直线 与两抛物线 , 共有两个公共点,求 的取值范围;
②抛物线 的顶点为 ,与 轴交点为点 , (点 在点 左侧),点 (不与点
重合)在第二象限内,且为 上任意一点,过点 作 轴,垂足为 ,直线 交
轴于点 ,连接 , .求证: .
第8页(共36页)第9页(共36页)2021年山东省德州市中考数学试卷
参考答案与试题解析
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正
确的选项选出来,每小题选对得4分,选错、不选或选出的答案超过一个均记分.
1.(4分)(2021•德州) 的相反数是
A. B.3 C. D.
【解答】解:根据相反数的定义,得 的相反数是 .
故选: .
2.(4分)(2021•德州)据国家统计局公布,我国第七次全国人口普查结果约为14.12亿
人,14.12亿用科学记数法表示为
A. B. C. D.
【解答】解:14.12亿 .
故选: .
3.(4分)(2021•德州)下列运算正确的是
A. B.
C. D.
【解答】解: ,故错误;
. ,故错误;
. ,故错误;
. ,正确.
故选: .
第10页(共36页)4.(4分)(2021•德州)如图所示的几何体,对其三视图叙述正确的是
A.左视图和俯视图相同 B.三个视图都不相同
C.主视图和左视图相同 D.主视图和俯视图相同
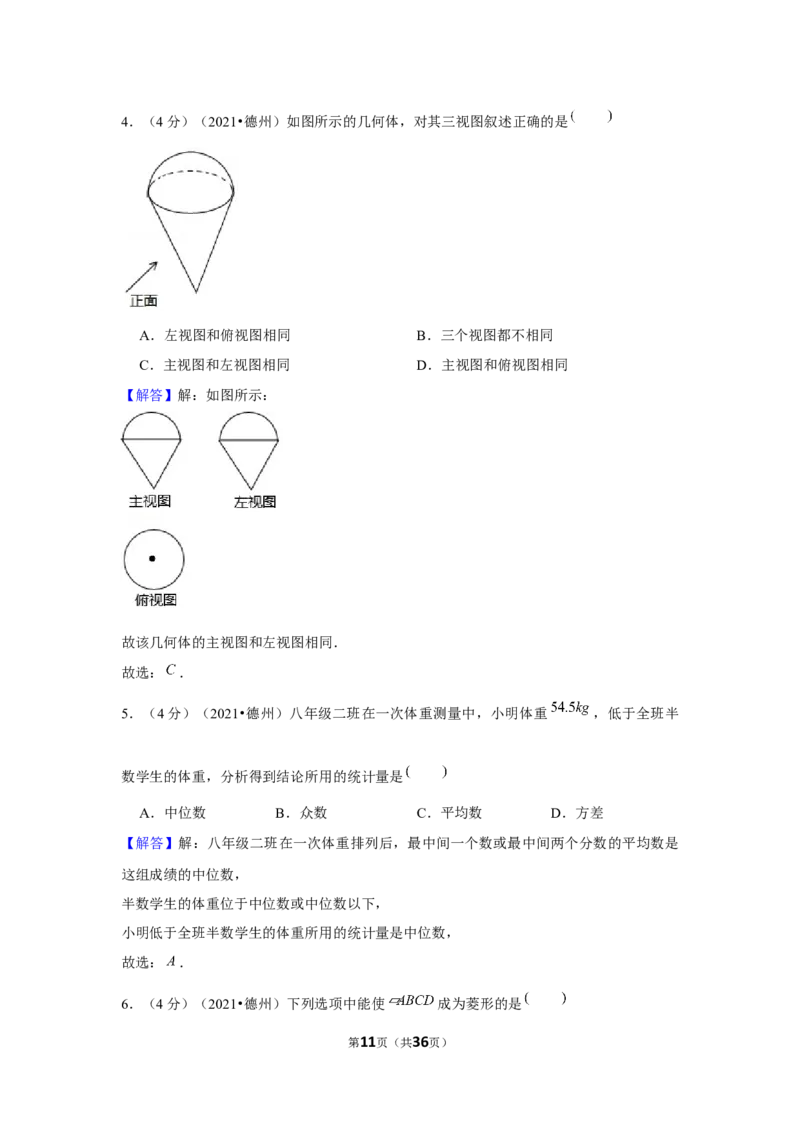
【解答】解:如图所示:
故该几何体的主视图和左视图相同.
故选: .
5.(4分)(2021•德州)八年级二班在一次体重测量中,小明体重 ,低于全班半
数学生的体重,分析得到结论所用的统计量是
A.中位数 B.众数 C.平均数 D.方差
【解答】解:八年级二班在一次体重排列后,最中间一个数或最中间两个分数的平均数是
这组成绩的中位数,
半数学生的体重位于中位数或中位数以下,
小明低于全班半数学生的体重所用的统计量是中位数,
故选: .
6.(4分)(2021•德州)下列选项中能使 成为菱形的是
第11页(共36页)A. B. C. D.
【解答】解: 、 四边形 是平行四边形,
,故选项 不符合题意;
、 四边形 是平行四边形, ,
为菱形,故选项 符合题意;
、 四边形 是平行四边形, ,
为矩形,故选项 不符合题意;
、 四边形 是平行四边形, ,
为矩形,故选项 不符合题意;
故选: .
7.(4分)(2021•德州)为响应“绿色出行”的号召,小王上班由自驾车改为乘坐公交
车.已知小王家距上班地点 ,他乘公交车平均每小时行驶的路程比他自驾车平均每小
时行驶的路程多 .他从家出发到上班地点,乘公交车所用的时间是自驾车所用时间的
.小王乘公交车上班平均每小时行驶
A. B. C. D.
【解答】解:设小王用自驾车方式上班平均每小时行驶 ,则乘公交车平均每小时行驶
,
由题意得: ,
解得: ,
经检验, 是原方程的解,
则 ,
即小王乘公交车上班平均每小时行驶 ,
故选: .
8.(4分)(2021•德州)如图,在矩形 中, , ,以点 为圆心,
长为半径画弧交 于点 ,连接 ,则阴影部分的面积为
第12页(共36页)A. B. C. D.
【解答】解: 四边形 是矩形, ,
, ,
,
,
, ,
,
阴影部分的面积
.
故选: .
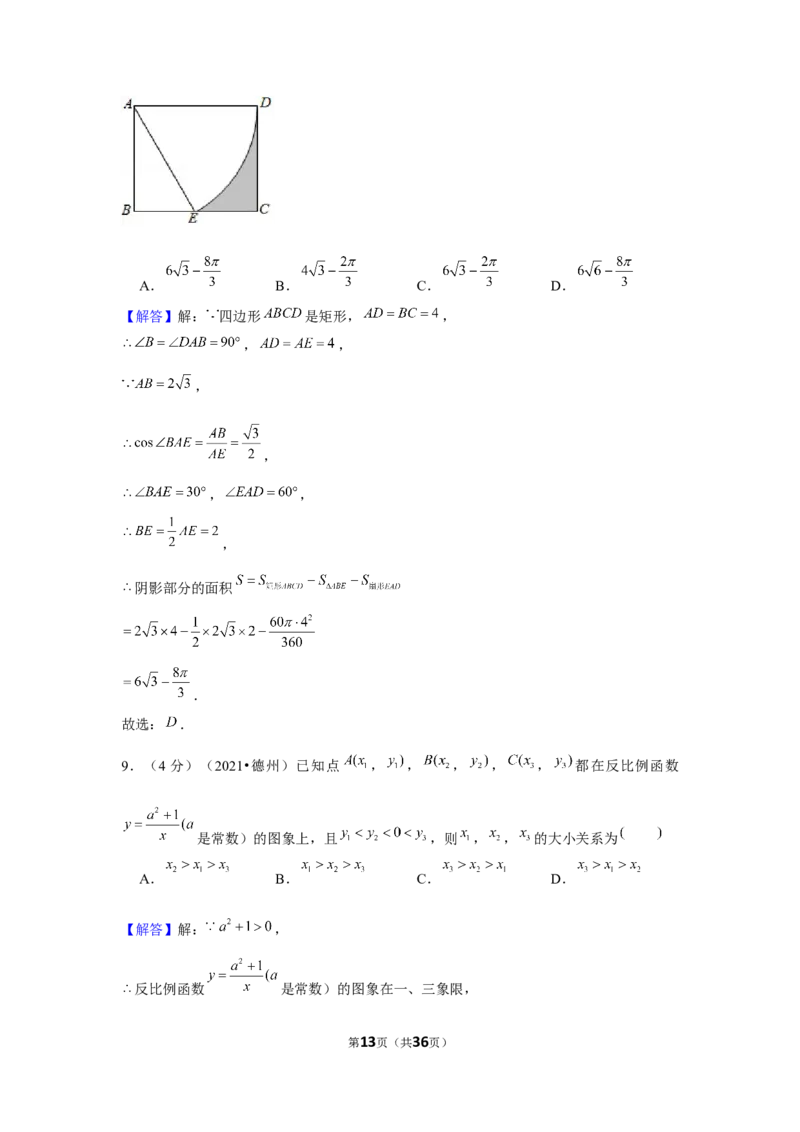
9.(4分)(2021•德州)已知点 , , , , , 都在反比例函数
是常数)的图象上,且 ,则 , , 的大小关系为
A. B. C. D.
【解答】解: ,
反比例函数 是常数)的图象在一、三象限,
第13页(共36页)如图所示,当 时, ,
故选: .
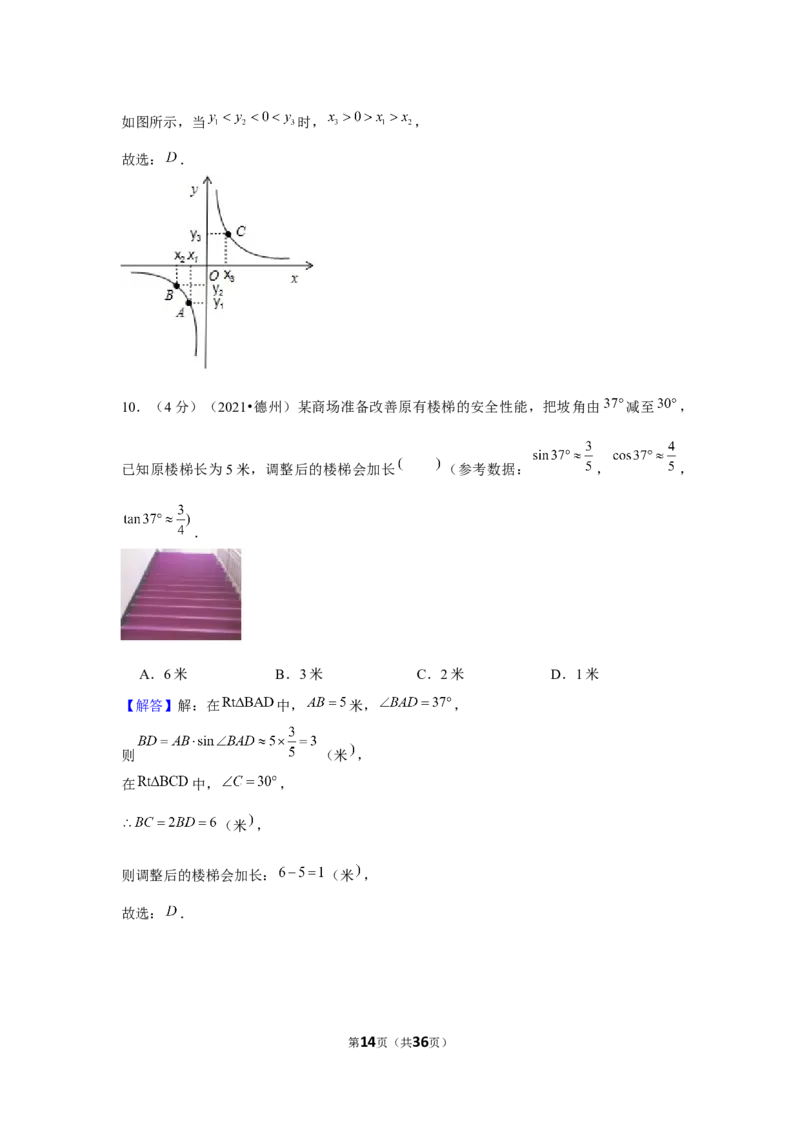
10.(4分)(2021•德州)某商场准备改善原有楼梯的安全性能,把坡角由 减至 ,
已知原楼梯长为5米,调整后的楼梯会加长 (参考数据: , ,
.
A.6米 B.3米 C.2米 D.1米
【解答】解:在 中, 米, ,
则 (米 ,
在 中, ,
(米 ,
则调整后的楼梯会加长: (米 ,
故选: .
第14页(共36页)11.(4分)(2021•德州)将含有 的三角板 按如图所示放置,点 在直线 上,
其中 ,分别过点 , 作直线 的平行线 , ,点 到直线 ,
的距离分别为 , ,则 的值为
A.1 B. C. D.
【解答】解:设 交 于点 ,
, ,
,
,
,
三角形 为等腰直角三角形,
在 中,设 长为 ,则 ,
第15页(共36页),
,
,
,
,
故选: .
12.(4分)(2021•德州)小红同学在研究函数 的图象时,发现有如下结论:
①该函数有最小值;②该函数图象与坐标轴无交点;③当 时, 随 的增大而增大;
④该函数图象关于 轴对称;⑤直线 与该函数图象有两个交点,则上述结论中正确的
个数为
A.2个 B.3个 C.4个 D.5个
【解答】解:列表:
1 2 3 4
5 4 5 5 4 5
画出函数图象如图,
第16页(共36页)观察图象:
①该函数有最小值,符合题意;
②该函数图象与坐标轴无交点,符合题意;
③当 时, 随 的增大而增大,不合题意;
④该函数图象关于 轴对称,符合题意;
⑤令 ,整理得 或 ,
△ ,
直线 与函数 和 各有两个交点,
直线 与该函数图象有四个交点,不符合题意,
综上,以上结论正确的有:①②④,
故选: .
二、填空题:本大题共6小题,共24分,只要求填写最后结果,每小题填对得4分.
13.(4分)(2021•德州)方程 的解为 , .
【解答】解:
或
,
故答案是: , .
14.(4分)(2021•德州)如图,点 , 在 上, , .请添加一个
条件 ,使 .
第17页(共36页)【解答】解: ,
,
,
添加 ,
在 和 中,
,
,
故答案为: .
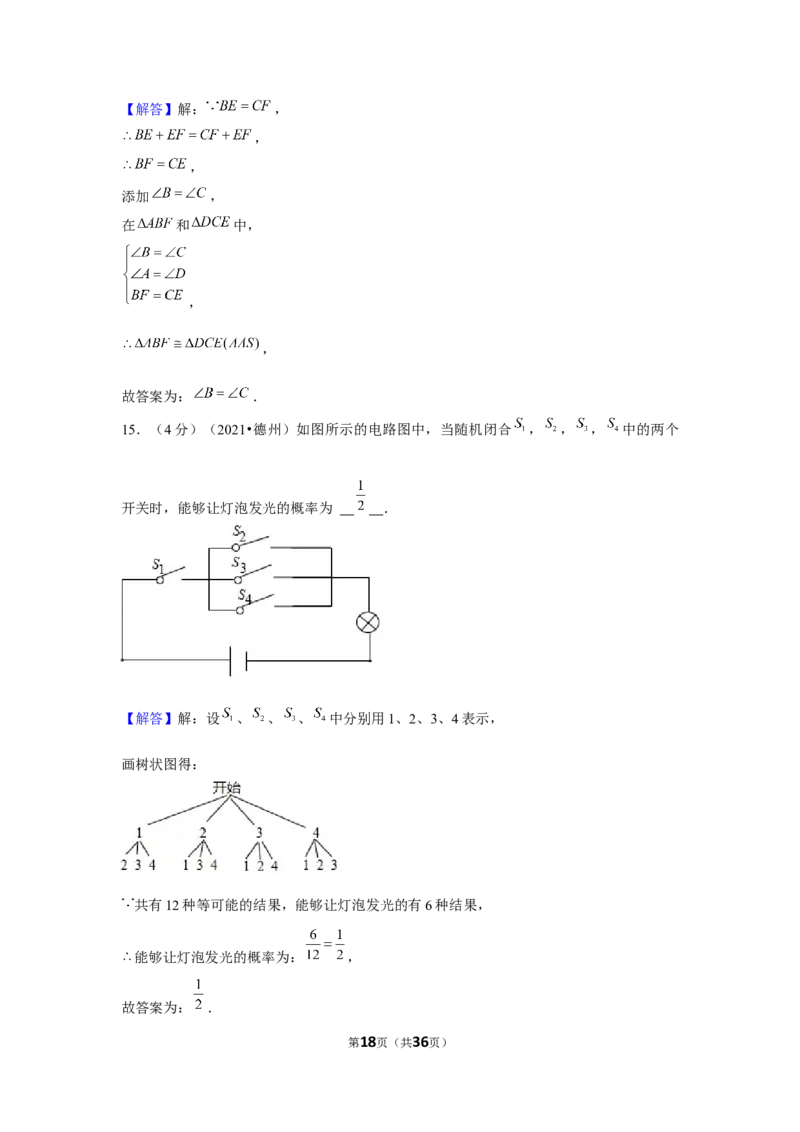
15.(4分)(2021•德州)如图所示的电路图中,当随机闭合 , , , 中的两个
开关时,能够让灯泡发光的概率为 .
【解答】解:设 、 、 、 中分别用1、2、3、4表示,
画树状图得:
共有12种等可能的结果,能够让灯泡发光的有6种结果,
能够让灯泡发光的概率为: ,
故答案为: .
第18页(共36页)16.(4分)(2021•德州)在平面直角坐标系 中,以点 为圆心,任意长为半径画弧,
交 轴正半轴于点 ,交 轴于点 ,再分别以点 , 为圆心,以大于 长为半径
画弧,两弧在 轴右侧相交于点 ,连接 ,若 ,则点 的坐标为 .
【解答】解:如图,
由作图知点 在第一象限角平分线上,
设点 的坐标为 , ,
,
,
,
,
故答案为 .
17.(4分)(2021•德州)小亮从学校步行回家,图中的折线反映了小亮离家的距离
(米 与时间 (分钟)的函数关系,根据图象提供的信息,给出以下结论:①他在前12
分钟的平均速度是70米 分钟;②他在第19分钟到家;③他在第15分钟离家的距离和第
24分钟离家的距离相等;④他在第33分钟离家的距离是 720米.其中正确的序号为
①④ .
第19页(共36页)【解答】解:由图象知,前12分中的平均速度为: (米 分),
故①正确;
由图象知,小亮第19分中又返回学校,
故②错误;
小亮在返回学校时的速度为: (米 分),
第15分离家距离: ,
从21分到41分小亮的速度为: (米 分),
第24分离家距离: (米 ,
,
故③错误;
小亮在33分离家距离: (米 ,
故④正确,
故答案为:①④.
18.(4分)(2021•德州)如图,在等边三角形 各边上分别截取 ,
交 延长线于点 , 交 延长线于点 , 交 延长线于
点 ;直线 , , 两两相交得到 ,若 ,则 2 .
第20页(共36页)【解答】解:延长 交 于点 ,
是等边三角形,
, ,
,
,
同理可得: ,
,
,
, ,
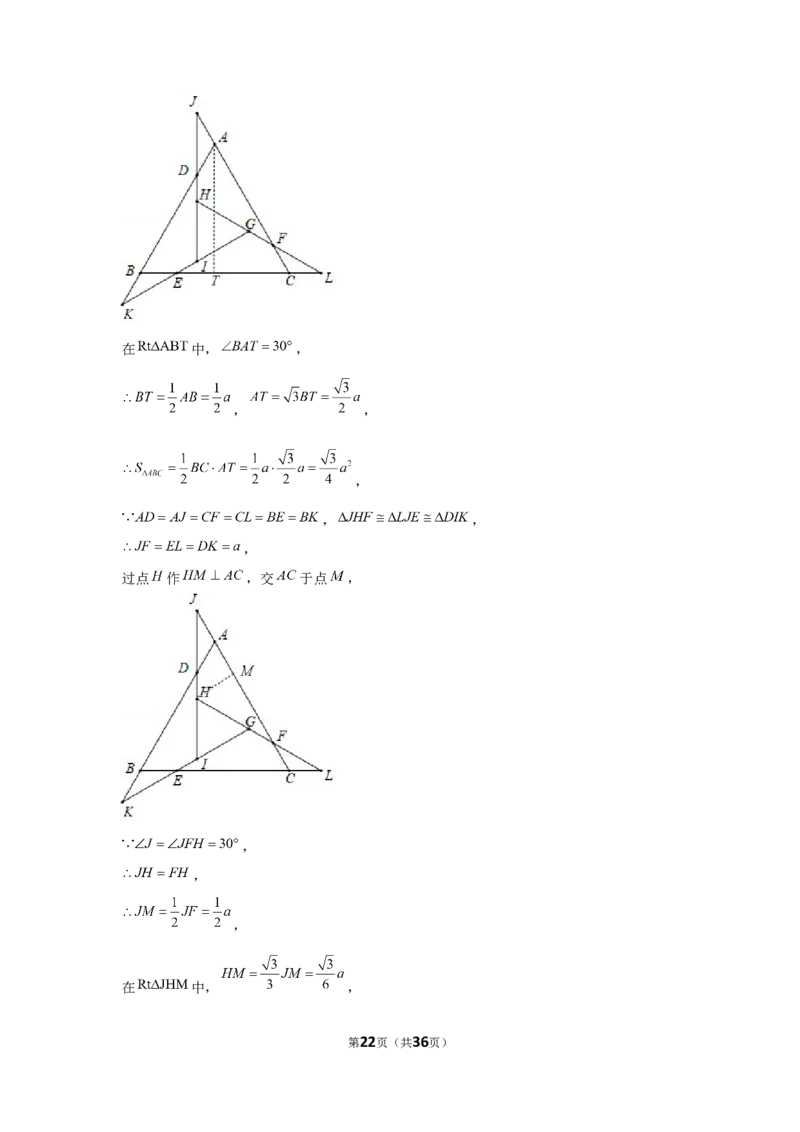
过点 作 ,交 于点 ,
设 ,
第21页(共36页)在 中, ,
, ,
,
, ,
,
过点 作 ,交 于点 ,
,
,
,
在 中, ,
第22页(共36页),
,
,
过点 作 ,交 于点 ,
设 ,
在 中, ,
, ,
,
,
,
解得: (负值舍去),
即 的值为2,
故答案为:2.
三、解答题:本大题共7小题,共78分.解答要写出必要的文字说明、证明过程或演算步骤.
第23页(共36页)19.(8分)(2021•德州)(1)计算: ;
(2)化简: .
【解答】解:(1)原式
;
(2)原式
.
20.(10分)(2021•德州)国家航天局消息北京时间2021年5月15日,我国首次火星着
陆任务宣告成功,某中学科技兴趣小组为了解本校学生对航天科技的关注程度,在该校内
进行了随机调查统计,将调查结果分为不关注、关注、比较关注、非常关注四类,回收、
整 理 好 全 部 调 查 问 卷 后 , 得 到 下 列 不 完 整 的 统 计 图 :
(1)此次调查中接受调查的人数为 5 0 人;
(2)补全图1条形统计图;
第24页(共36页)(3)扇形统计图中,“关注”对应扇形的圆心角为 ;
(4)该校共有900人,根据调查结果估计该校“关注”,“比较关注”及“非常关注”航
天科技的人数共多少人?
【解答】解:(1)不关注、关注、比较关注的共有 (人 ,占调查人数的
,
此次调查中接受调查的人数为 (人 ,
故答案为:50;
(2) (人 ,
补全统计图如图所示:
(3) ,
故答案为: ;
(4) (人 ,
答:估计该校“关注”,“比较关注”及“非常关注”航天科技的人数共有828人.
21.(10分)(2021•德州)已知点 为函数 图象上任意一点,连接 并延
长至点 ,使 ,过点 作 轴交函数图象于点 ,连接 .
第25页(共36页)(1)如图1,若点 的坐标为 ,求点 的坐标;
(2)如图2,过点 作 ,垂足为 ,求四边形 的面积.
【解答】解:(1)将点 坐标代入到反比例函数 中得,
,
,
点 的坐标为 ,
, ,
点 的坐标为 ,
轴,
点 的纵坐标为2,
令 ,则 ,
,
点 的坐标为 ;
(2) 轴,
轴,
又 ,
轴,
的横坐标为4,
第26页(共36页)在 上,
的纵坐标为2,
,
,
,
四边形 的面积为: .
22.(12分)(2021•德州)如图,点 , 分别在正方形 的边 , 上,且
,点 , 分别在边 , 上,且 ,垂足为 .
(1)求证: ;
(2)若正方形 边长为5, , ,求 的长度.
【解答】(1)证明: 四边形 是正方形,
, ,
,
,
,
,
,
,
即 ,
在 和 中,
第27页(共36页),
,
;
(2)解: , ,
,
在 中, ,
即 ,
,
,
在 中, ,
, ,
,
,
即 ,
,
.
23.(12分)(2021•德州)某公司分别在 , 两城生产同种产品,共100件. 城生
产产品的成本 (万元)与产品数量 (件 之间具有函数关系 , 城生
产产品的每件成本为60万元.
(1)当 城生产多少件产品时, , 两城生产这批产品成本的和最小,最小值是多少?
(2)从 城把该产品运往 , 两地的费用分别为1万元 件和3万元 件;从 城把该
产品运往 , 两地的费用分别为1万元 件和2万元 件. 地需要90件, 地需要10
件,在(1)的条件下,怎样调运可使 , 两城运费的和最小?
第28页(共36页)【解答】解:(1)设 , 两城生产这批产品的总成本的和为 (万元),
则
,
当 时, 取得最小值,最小值为5700万元,
城生产20件, , 两城生产这批产品成本的和最小,最小值是5700万元;
(2)设从 城把该产品运往 地的产品数量为 件,则从 城把该产品运往 地的产品
数量为 件;
从 城把该产品运往 地的产品数量为 件,则从 城把该产品运往 地的产品数
量为 件,运费的和为 ,
由题意得: ,
解得 ,
,
根据一次函数的性质可得:
随 的增大而减小,
当 时, 取得最小值,最小值为110.
24.(12分)(2021•德州)已知 为 的外接圆, .
(1)如图1,延长 至点 ,使 ,连接 .
①求证: 为直角三角形;
②若 的半径为4, ,求 的值;
(2)如图2,若 , 为 上的一点,且点 , 位于 两侧,作
第29页(共36页)关于 对称的图形 ,连接 ,试猜想 , , 三者之间的数量关系并给
予证明.
【解答】证明:(1)① , ,
.
.
为直角三角形;
解:②连接 , ,如图,
,
,
且 .
的半径为4,
.
设 ,则 ,
第30页(共36页),
,
.
解得: .
.
由①知: ,
,
.
,
.
(2) , , 三者之间的数量关系为: .理由:
延长 交 于点 ,连接 , ,如图,
, ,
.
, .
.
.
与 关于 对称,
第31页(共36页),
,
.
.
.
即 .
,
.
在 和 中,
,
.
.
.
25.(14分)(2021•德州)小刚在用描点法画抛物线 时,列出了下面
的表格:
0 1 2 3 4
3 6 7 6 3
(1)请根据表格中的信息,写出抛物线 的一条性质: 抛物线的顶点坐标为 ;
(2)求抛物线 的解析式;
第32页(共36页)(3)将抛物线 先向下平移3个单位长度,再向左平移4个单位长度,得到新的抛物线
;
①若直线 与两抛物线 , 共有两个公共点,求 的取值范围;
②抛物线 的顶点为 ,与 轴交点为点 , (点 在点 左侧),点 (不与点
重合)在第二象限内,且为 上任意一点,过点 作 轴,垂足为 ,直线 交
轴于点 ,连接 , .求证: .
【解答】解:(1) 表中的数据关于 对称,
该抛物线的顶点为 .
故答案为:抛物线的顶点坐标为 ;
(2)由题意抛物线的解析式为 ,将表中的三对对应值代入得:
,
第33页(共36页)解得: .
抛物线 的解析式为 .
(3)①由(1)知:抛物线 的顶点为 ,
将抛物线 先向下平移3个单位长度,再向左平移4个单位长度,得到新的抛物线 的
顶点为 .
抛物线 的解析式为 .
将 代入 得: ,
将 代入 得: ,
直线 与两抛物线 , 共有两个公共点,
.
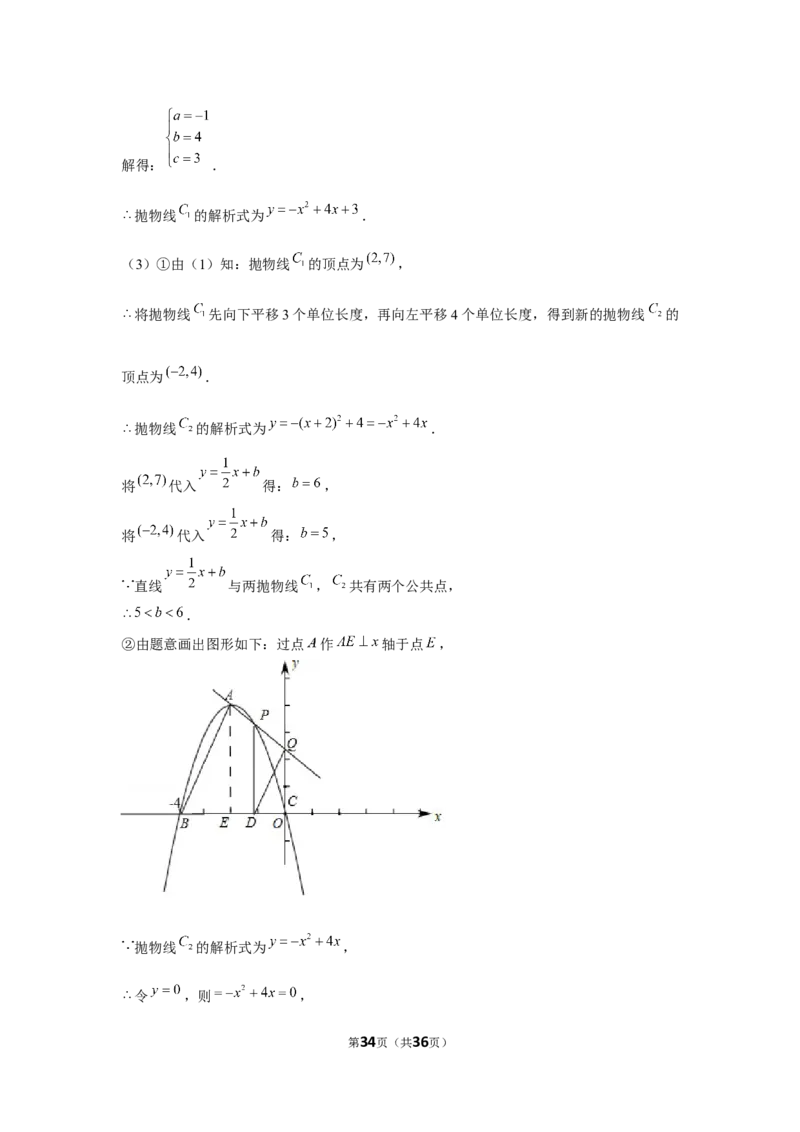
②由题意画出图形如下:过点 作 轴于点 ,
抛物线 的解析式为 ,
令 ,则 ,
第34页(共36页)解得: 或 .
抛物线 与 轴交点为点 , (点 在点 左侧),
, , .
.
由①知:抛物线 的顶点为 .
, ,
.
在 中, .
点 (不与点 重合)在第二象限内,且为 上任意一点,
设点 ,则 , .
轴,
.
设直线 的解析式为 ,则:
,
解得: .
直线 的解析式为 .
令 ,则 .
.
.
在 中, .
第35页(共36页).
.
.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/9/14 18:44:02;用户:初中数学61;邮箱:ydyd61@xyh.com;学号:36810736
第36页(共36页)