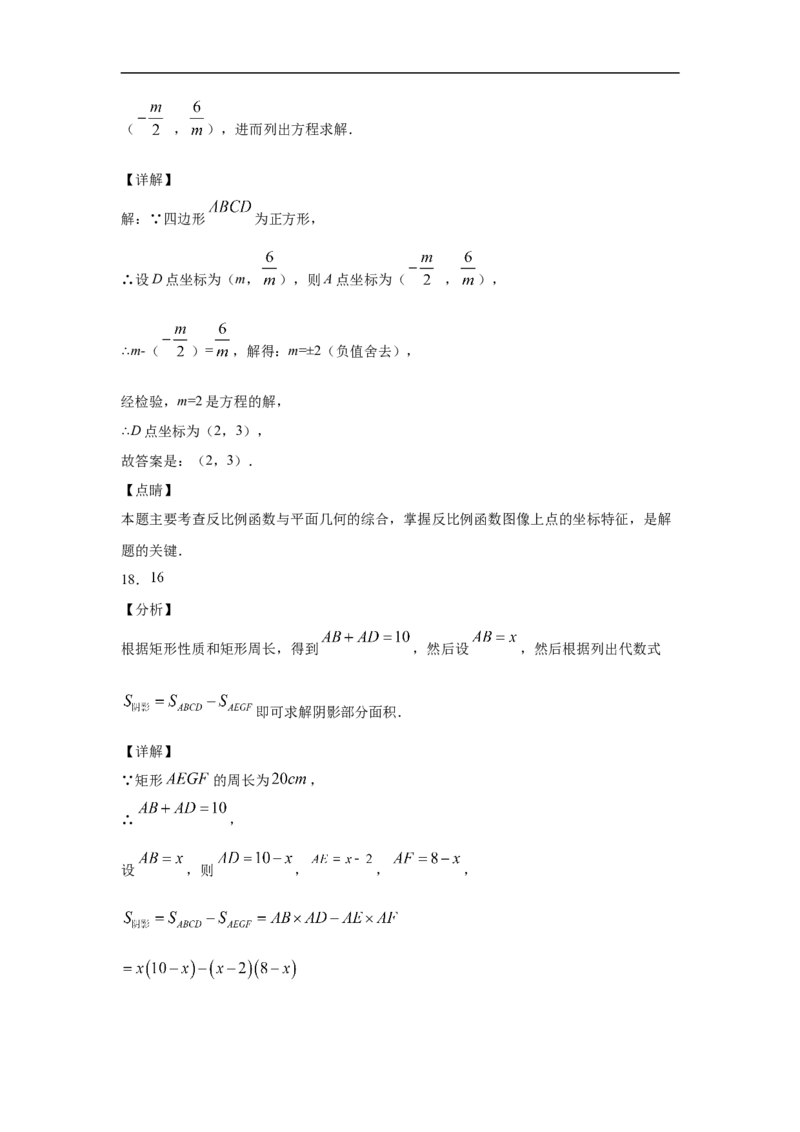文档内容
江苏省徐州市2021年中考数学真题与答案解析
一、单选题
1.-3 的相反数是( )
A.3 B.-3 C. D.
2.下列图形,是轴对称图形但不是中心对称图形的是( )
A. B.
C. D.
3.下列计算正确的是( )
A. B. C. D.
4.甲、乙两个不透明的袋子中各有三种颜色的糖果若干,这些糖果除颜色外无其他差
别.具体情况如下表所示.
袋子 糖
红色 黄色 绿色 总计
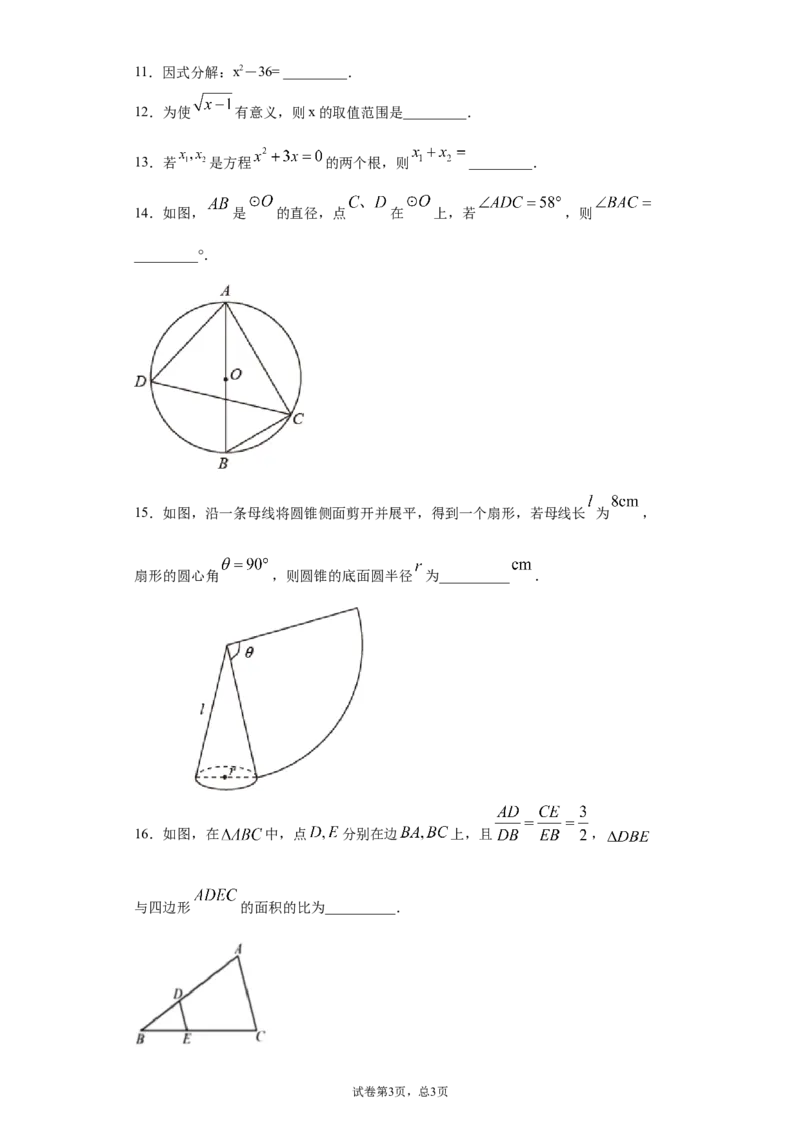
果
甲袋 2颗 2颗 1颗 5颗
乙袋 4颗 2颗 4颗 10颗
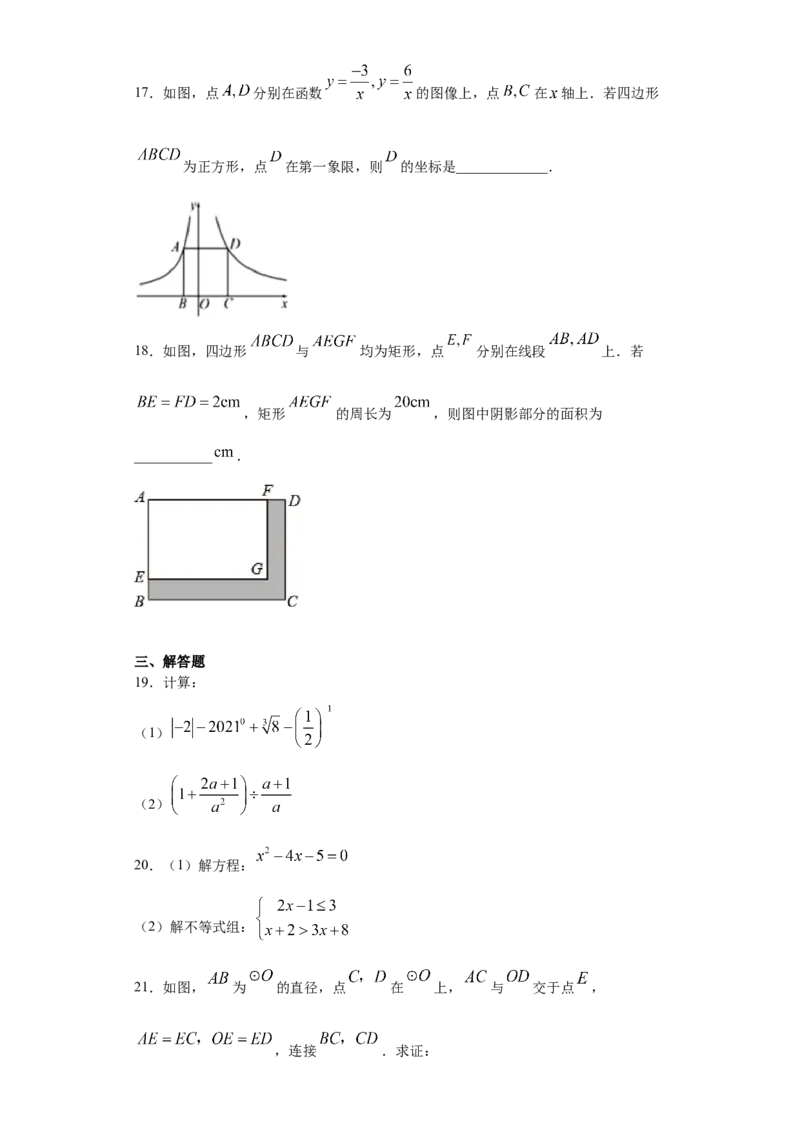
若小明从甲、乙两个袋子中各随机摸出一颗糖果,则他从甲袋比从乙袋( )
A.摸出红色糖果的概率大 B.摸出红色糖果的概率小
C.摸出黄色糖果的概率大 D.摸出黄色糖果的概率小
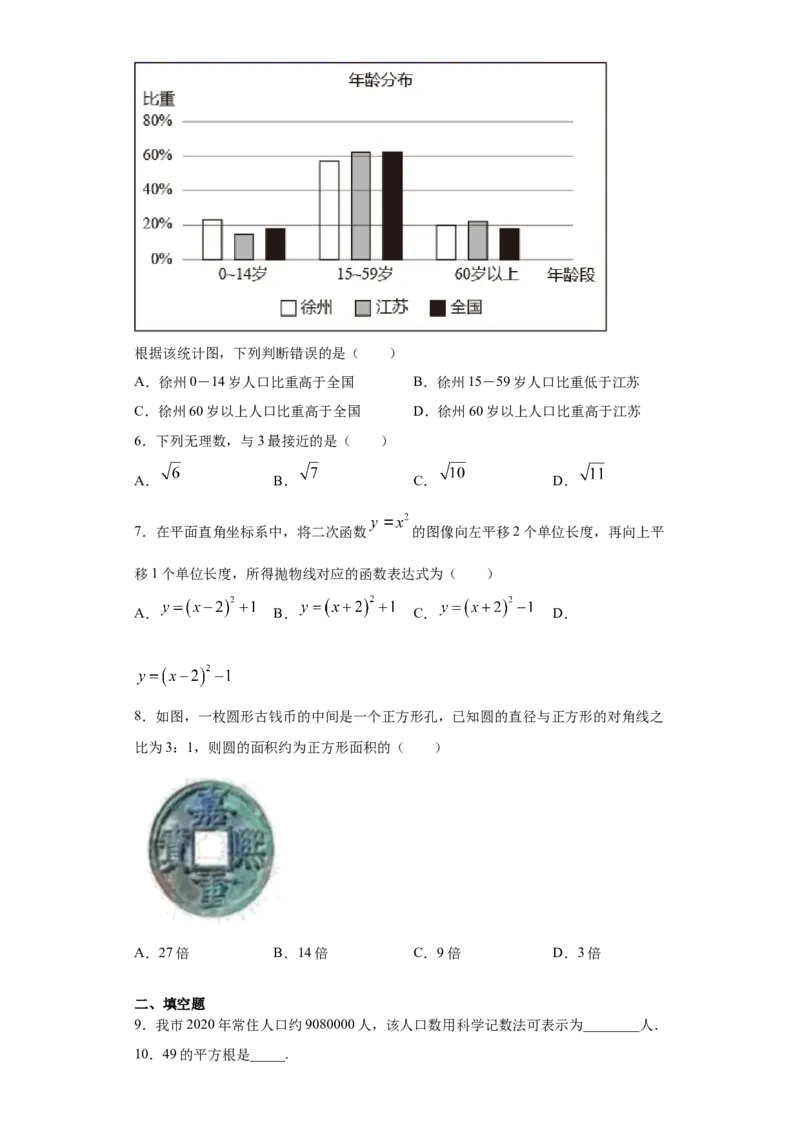
5.第七次全国人民普查的部分结果如图所示.
试卷第1页,总3页根据该统计图,下列判断错误的是( )
A.徐州0-14岁人口比重高于全国 B.徐州15-59岁人口比重低于江苏
C.徐州60岁以上人口比重高于全国 D.徐州60岁以上人口比重高于江苏
6.下列无理数,与3最接近的是( )
A. B. C. D.
7.在平面直角坐标系中,将二次函数 的图像向左平移2个单位长度,再向上平
移1个单位长度,所得抛物线对应的函数表达式为( )
A. B. C. D.
8.如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之
比为3:1,则圆的面积约为正方形面积的( )
A.27倍 B.14倍 C.9倍 D.3倍
二、填空题
9.我市2020年常住人口约9080000人,该人口数用科学记数法可表示为________人.
10.49的平方根是_____.11.因式分解:x2-36= _________.
12.为使 有意义,则x的取值范围是_________.
13.若 是方程 的两个根,则 _________.
14.如图, 是 的直径,点 在 上,若 ,则
_________°.
15.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若母线长 为 ,
扇形的圆心角 ,则圆锥的底面圆半径 为__________ .
16.如图,在 中,点 分别在边 上,且 ,
与四边形 的面积的比为__________.
试卷第3页,总3页17.如图,点 分别在函数 的图像上,点 在 轴上.若四边形
为正方形,点 在第一象限,则 的坐标是_____________.
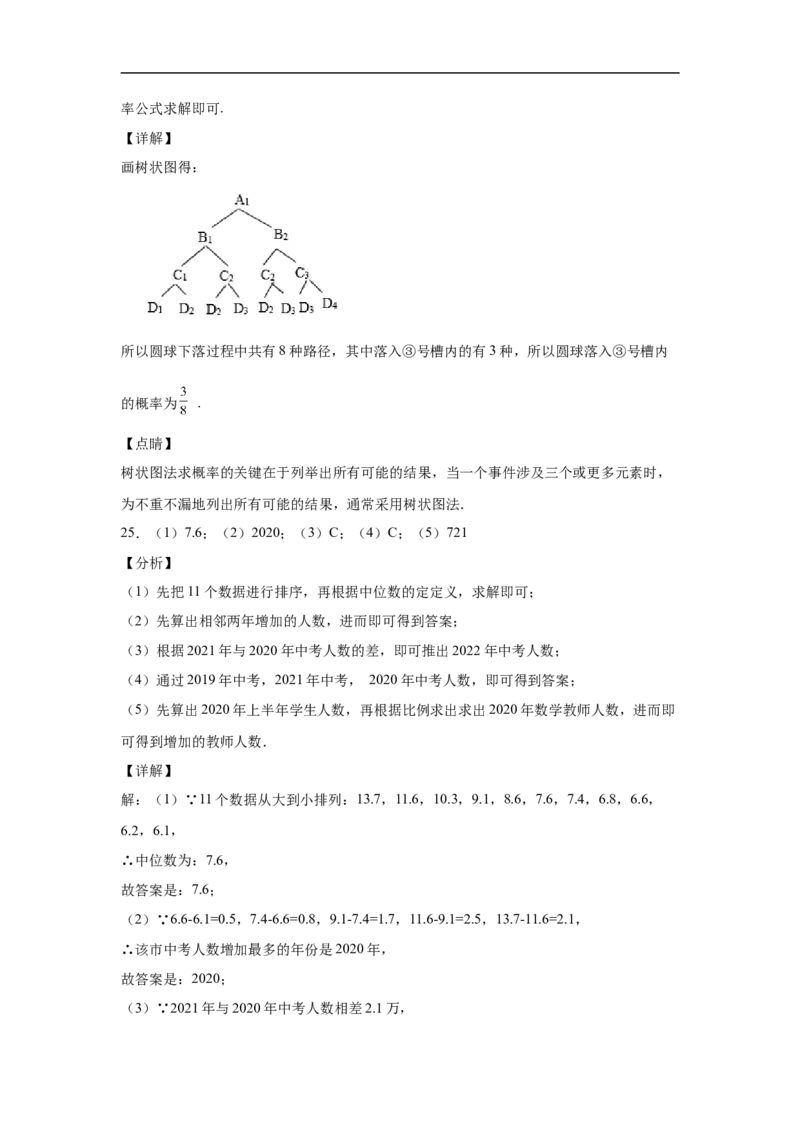
18.如图,四边形 与 均为矩形,点 分别在线段 上.若
,矩形 的周长为 ,则图中阴影部分的面积为
___________ .
三、解答题
19.计算:
(1)
(2)
20.(1)解方程:
(2)解不等式组:
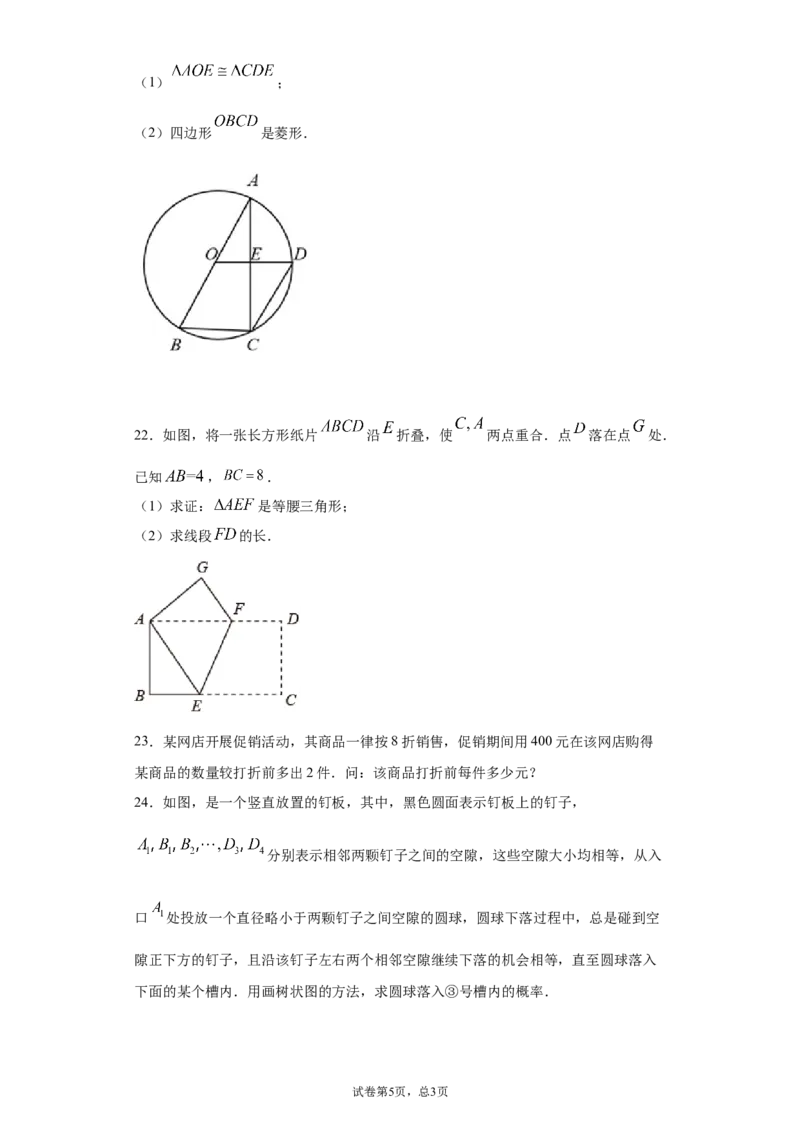
21.如图, 为 的直径,点 在 上, 与 交于点 ,
,连接 .求证:(1) ;
(2)四边形 是菱形.
22.如图,将一张长方形纸片 沿 折叠,使 两点重合.点 落在点 处.
已知 , .
(1)求证: 是等腰三角形;
(2)求线段 的长.
23.某网店开展促销活动,其商品一律按8折销售,促销期间用400元在该网店购得
某商品的数量较打折前多出2件.问:该商品打折前每件多少元?
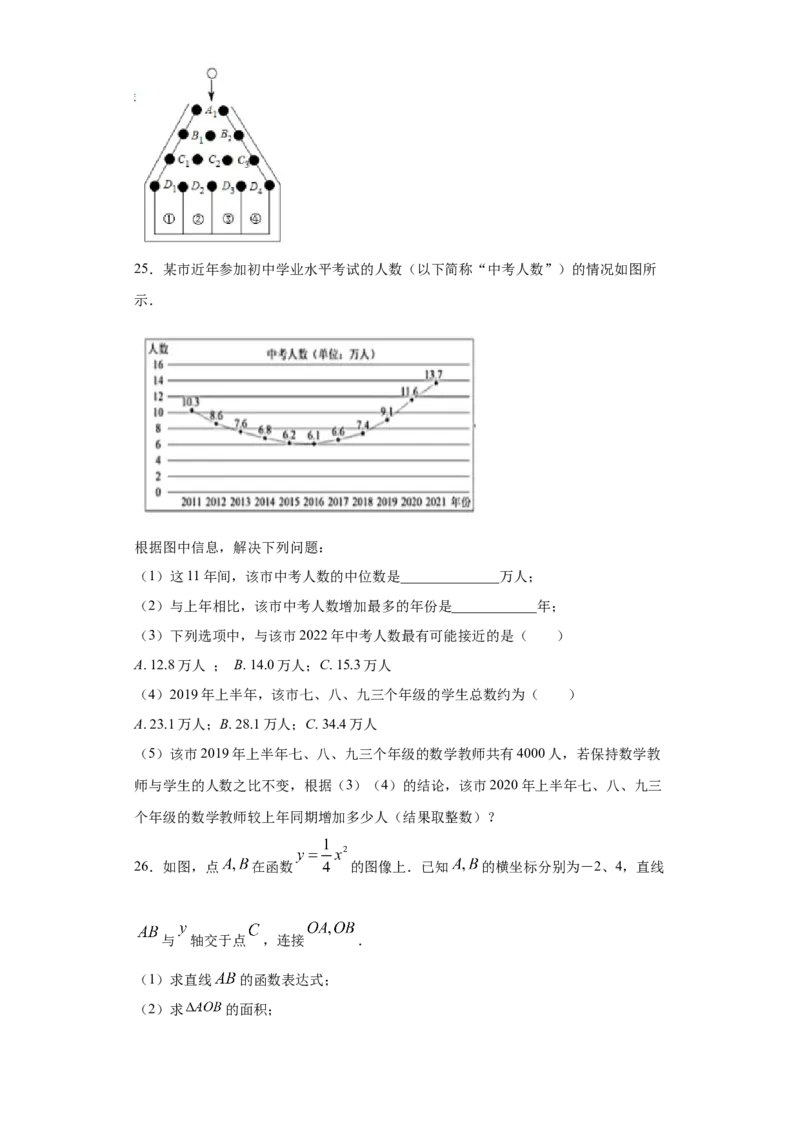
24.如图,是一个竖直放置的钉板,其中,黑色圆面表示钉板上的钉子,
分别表示相邻两颗钉子之间的空隙,这些空隙大小均相等,从入
口 处投放一个直径略小于两颗钉子之间空隙的圆球,圆球下落过程中,总是碰到空
隙正下方的钉子,且沿该钉子左右两个相邻空隙继续下落的机会相等,直至圆球落入
下面的某个槽内.用画树状图的方法,求圆球落入③号槽内的概率.
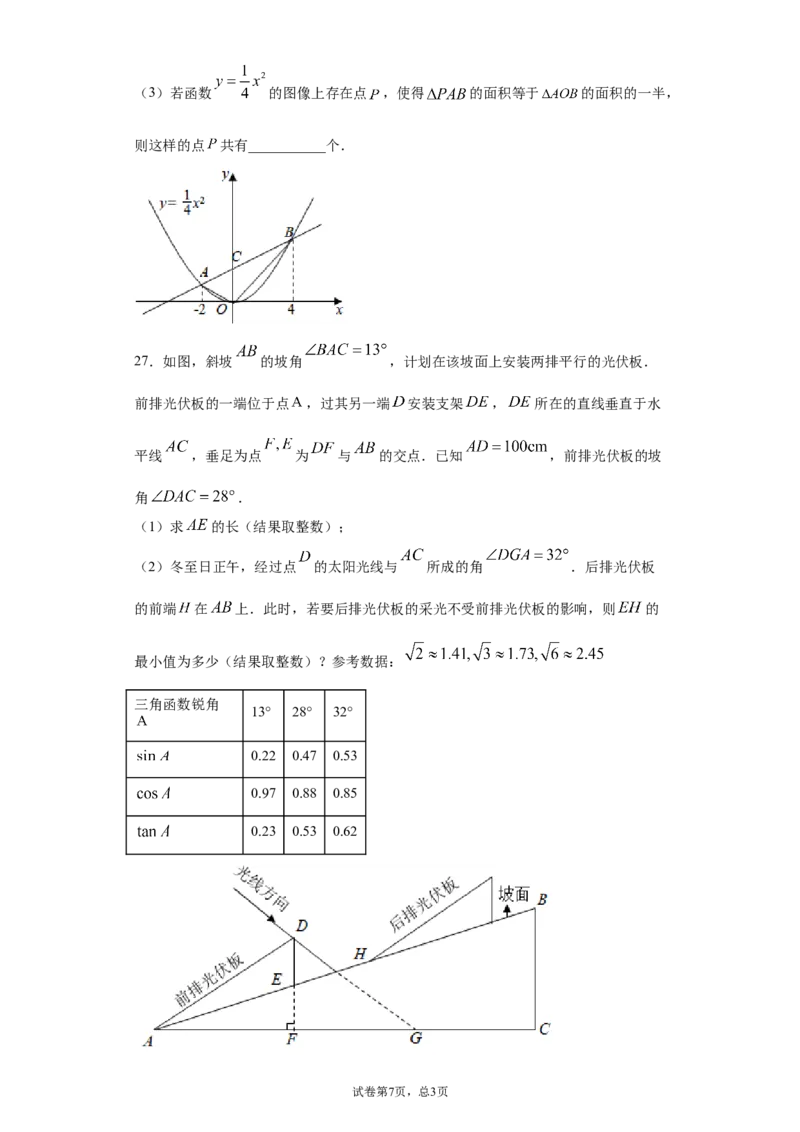
试卷第5页,总3页25.某市近年参加初中学业水平考试的人数(以下简称“中考人数”)的情况如图所
示.
根据图中信息,解决下列问题:
(1)这11年间,该市中考人数的中位数是______________万人;
(2)与上年相比,该市中考人数增加最多的年份是____________年;
(3)下列选项中,与该市2022年中考人数最有可能接近的是( )
A. 12.8万人 ; B. 14.0万人;C. 15.3万人
(4)2019年上半年,该市七、八、九三个年级的学生总数约为( )
A. 23.1万人;B. 28.1万人;C. 34.4万人
(5)该市2019年上半年七、八、九三个年级的数学教师共有4000人,若保持数学教
师与学生的人数之比不变,根据(3)(4)的结论,该市2020年上半年七、八、九三
个年级的数学教师较上年同期增加多少人(结果取整数)?
26.如图,点 在函数 的图像上.已知 的横坐标分别为-2、4,直线
与 轴交于点 ,连接 .
(1)求直线 的函数表达式;
(2)求 的面积;(3)若函数 的图像上存在点 ,使得 的面积等于 的面积的一半,
则这样的点 共有___________个.
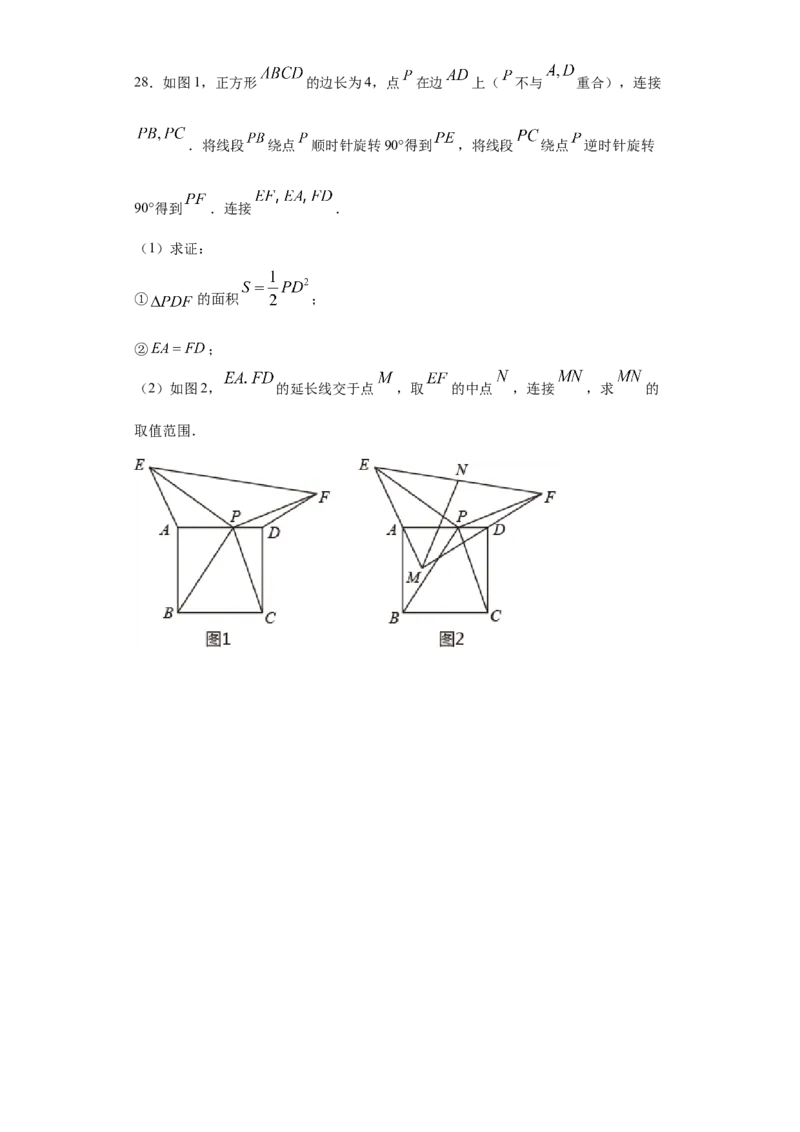
27.如图,斜坡 的坡角 ,计划在该坡面上安装两排平行的光伏板.
前排光伏板的一端位于点 ,过其另一端 安装支架 , 所在的直线垂直于水
平线 ,垂足为点 为 与 的交点.已知 ,前排光伏板的坡
角 .
(1)求 的长(结果取整数);
(2)冬至日正午,经过点 的太阳光线与 所成的角 .后排光伏板
的前端 在 上.此时,若要后排光伏板的采光不受前排光伏板的影响,则 的
最小值为多少(结果取整数)?参考数据:
三角函数锐角
13° 28° 32°
0.22 0.47 0.53
0.97 0.88 0.85
0.23 0.53 0.62
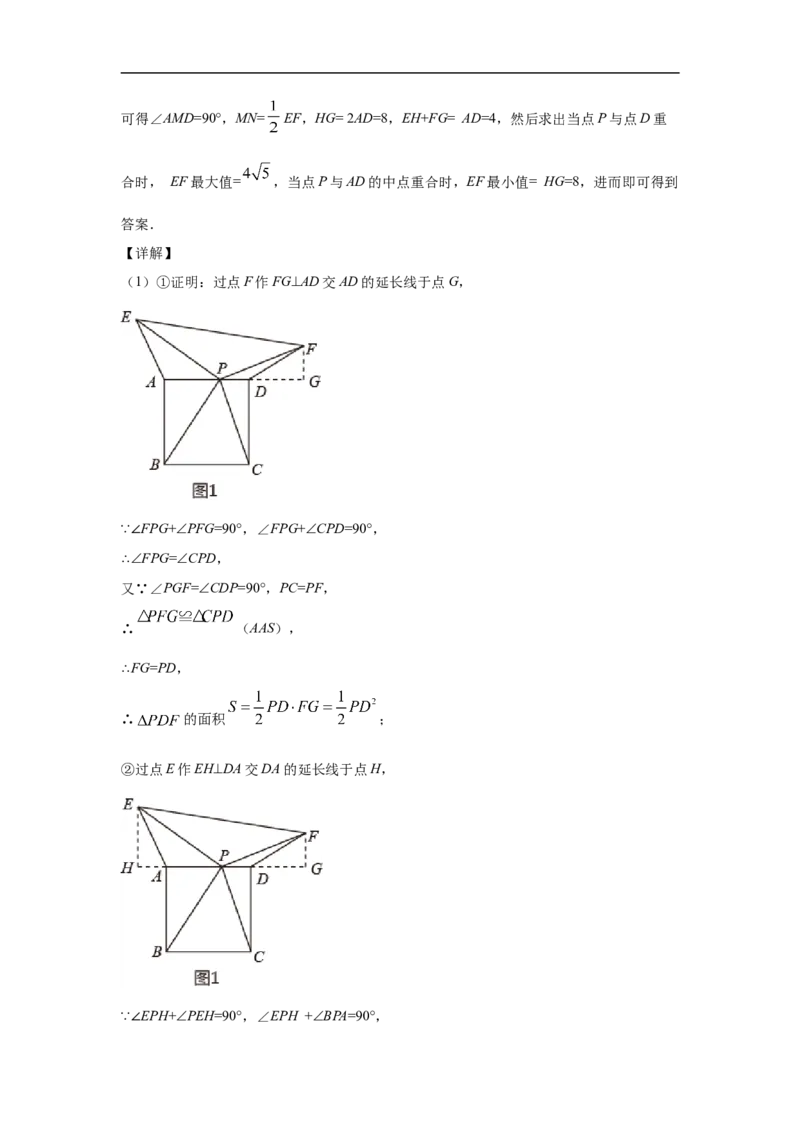
试卷第7页,总3页28.如图1,正方形 的边长为4,点 在边 上( 不与 重合),连接
.将线段 绕点 顺时针旋转90°得到 ,将线段 绕点 逆时针旋转
90°得到 .连接 .
(1)求证:
① 的面积 ;
② ;
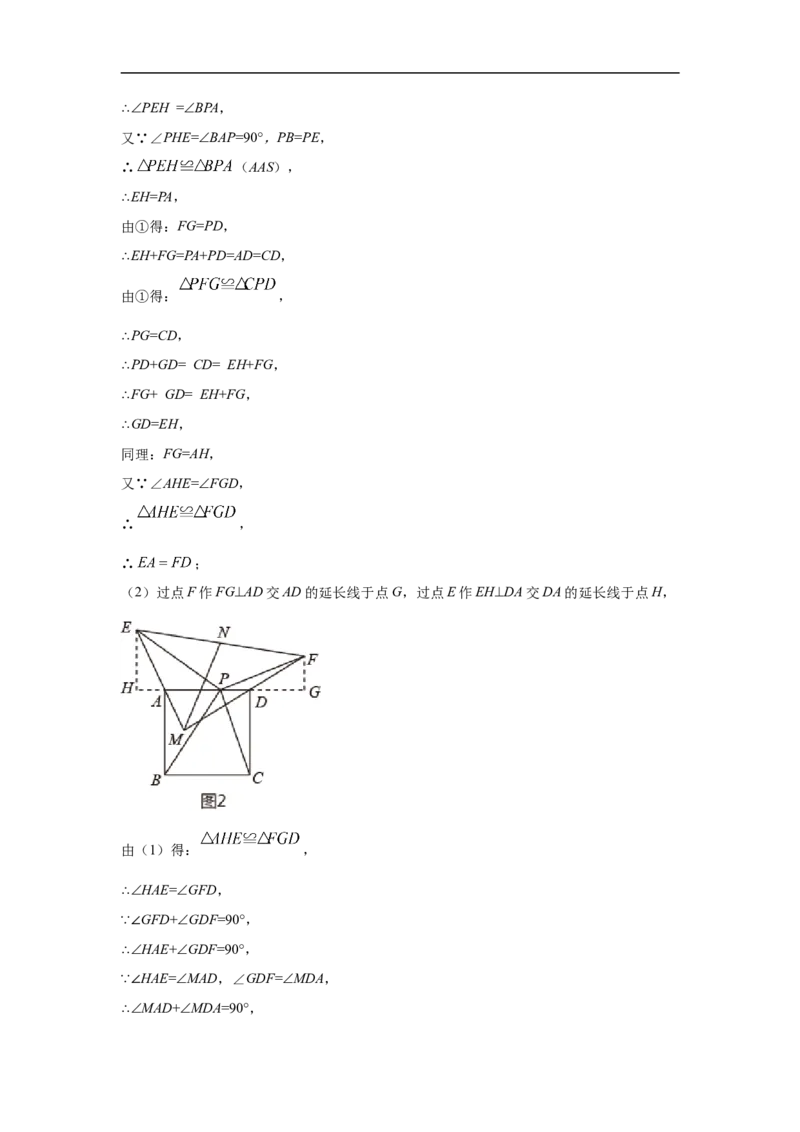
(2)如图2, 的延长线交于点 ,取 的中点 ,连接 ,求 的
取值范围.参考答案
1.A
【分析】
根据相反数的定义,直接得到答案即可.
【详解】
解:-3 的相反数是:3,
故选A.
【点睛】
本题主要考查求相反数,掌握相反数的定义,是解题的关键.
2.D
【分析】
根据轴对称图形和中心对称图形的定义对选项逐一分析即可
【详解】
A.不是轴对称图形,也不是中心对称图形,不符合题意;
B.是轴对称图形,也是中心对称图形,不符合题意;
C.不是轴对称图形,是中心对称图形,不符合题意;
D. 是轴对称图形但不是中心对称图形,符合题意
故选D
【点睛】
本题考查了轴对称图形和中心对称图形的定义,了解轴对称图形和中心对称图形的定义是
解题的关键.
3.A
【分析】
根据幂的乘方,同底数幂的乘法,合并同类项,同底数幂的除法法则对选项逐一判断即可
【详解】
A. ,符合题意;
B. ,不符合题意;
C. ,不符合题意;
D. ,不符合题意故选A
【点睛】
本题考查了幂的乘方,同底数幂的乘法,合并同类项,同底数幂的除法,熟悉以上运算法
则是解题的关键.
4.C
【分析】
分别对甲乙两个袋子的红色及黄色的糖果的概率进行计算,再去比较即可.
【详解】
解:P(甲袋摸出红色糖果) ,
P(甲袋摸出黄色糖果) ,
P(乙袋摸出红色糖果) ,
P(乙袋摸出黄色糖果) ,
∴P(甲袋摸出红色糖果)=P(乙袋摸出红色糖果),故A,B错误;
P(甲袋摸出黄色糖果)>P(乙袋摸出黄色糖果),故D错误,C正确.
故选:C.
【点睛】
本题主要考查了简单概率的计算,掌握概率公式并能灵活掌握是解题关键.
5.D
【分析】
根据题目中的条形统计图对四个选项依次判断即可.
【详解】
解:根据题目中的条形统计图可知:
徐州0-14岁人口比重高于全国,A选项不符合题意;
徐州15-59岁人口比重低于江苏,B选项不符合题意;
徐州60岁以上人口比重高于全国,C选项不符合题意;
徐州60岁以上人口比重低于江苏,D选项符合题意.故选:D.
【点睛】
本题考查条形统计图的分析,正确从条形统计图中读取数据是解题关键.
6.C
【分析】
先比较各个数平方后的结果,进而即可得到答案.
【详解】
解:∵32=9,( )2=6,( )2=7,( )2=10,( )2=11,
∴与3最接近的是 ,
故选C.
【点睛】
本题主要考查无理数的估计,理解算术平方根与平方的关系,是解题的关键.
7.B
【分析】
先求出平移后抛物线的顶点坐标,进而即可得到答案.
【详解】
解:∵ 的顶点坐标为(0,0)
∴将二次函数 的图像向左平移2个单位长度,再向上平移1个单位长度,所得抛物
线的顶点坐标为(-2,1),
∴所得抛物线对应的函数表达式为 ,
故选B
【点睛】
本题主要考查二次函数的平移规律,找出平移后二次函数图像的顶点坐标或掌握“左加右
减,上加下减”,是解题的关键.
8.C
【分析】
设OB=x,则OA=3x,BC=2x,根据圆的面积公式和正方形的面积公式,求出面积,进而即
可求解.【详解】
解:由圆和正方形的对称性,可知:OA=OD,OB=OC,
∵圆的直径与正方形的对角线之比为3:1,
∴设OB=x,则OA=3x,BC=2x,
∴圆的面积=π(3x)2=9πx2,正方形的面积= =2x2,
∴9πx2÷2x2= ,即:圆的面积约为正方形面积的14倍,
故选C.
【点睛】
本题主要考查圆和正方形的面积以及对称性,根据题意画出图形,用未知数表示各个图形
的面积,是解题的关键.
9.9.08×106
【分析】
科学记数法的表示形式为a×10n,其中1≤a<10且n为正整数.
【详解】
9080000=9.08×106,
故答案为:9.08×106
【点睛】
本题考查了科学记数法,关键是要准确确定a及n的值.
10.±7
【详解】
∵(±7)2=49,∴49的平方根是±7.
故答案为±7
【点睛】
如果个一个数x的平方等于a,即x2=a,那么这个数x叫做a的平方根.正数a有两个平方根,
它们互为相反数;0的平方根是0;负数没有平方根.
11.(x+6)(x-6)
【分析】
根据平方差公式解答即可.
【详解】
解:x2-36=(x+6)(x-6);
故答案为:(x+6)(x-6).
【点睛】
本题考查了多项式的因式分解,属于基础题目,掌握平方差公式是解答的关键.
12.x≥1
【详解】
试题分析:根据二次根式的被开方数为非负数,可知x-1≥0,解得x≥1.
考点:二次根式
13.-3
【分析】
根据一元二次方程根与系数的关系,即可求解.
【详解】
解:∵ 是方程 的两个根,
∴ ,
故答案是:-3.
【点睛】
本题主要考查一元二次方程根与系数的关系,掌握 是一元二次方程 的
两个根,则 ,是解题的关键.14.
【分析】
由同弧所对的圆周角相等和直径所对的圆周角为90°然后根据三角形内角和即可求出
的度数.
【详解】
∵ ,
∴ ,
又∵AB是直径,
∴ ,
∴ .
故答案为: .
【点睛】
此题考查了同弧所对圆周角的性质和直径所对圆周角的性质,解题的关键是熟练掌握同弧
所对圆周角的性质和直径所对圆周角的性质.
15.2
【分析】
结合题意,根据弧长公式,得圆锥的底面圆周长;再根据圆形周长的性质计算,即可得到
答案.
【详解】
∵母线长 为 ,扇形的圆心角
∴圆锥的底面圆周长
∴圆锥的底面圆半径
故答案为:2.
【点睛】
本题考查了弧长、圆周长的知识;解题的关键是熟练掌握弧长计算的性质,从而完成求解.16.
【分析】
先证明 ,再根据相似三角形的性质,即可得到 ,进而即可
求解.
【详解】
解:∵ ,
∴
∴
∵∠B=∠B,
∴ ,
∴
∴ 与四边形 的面积的比= .
故答案是: .
【点睛】
本题主要考查相似三角形的判定和性质,掌握相似三角形的面积比等于相似比的平方,是
解题的关键.
17.(2,3)
【分析】
根据正方形和反比例函数图像上点的坐标特征,设D点坐标为(m, ),则A点坐标为( , ),进而列出方程求解.
【详解】
解:∵四边形 为正方形,
∴设D点坐标为(m, ),则A点坐标为( , ),
∴m-( )= ,解得:m=±2(负值舍去),
经检验,m=2是方程的解,
∴D点坐标为(2,3),
故答案是:(2,3).
【点睛】
本题主要考查反比例函数与平面几何的综合,掌握反比例函数图像上点的坐标特征,是解
题的关键.
18.
【分析】
根据矩形性质和矩形周长,得到 ,然后设 ,然后根据列出代数式
即可求解阴影部分面积.
【详解】
∵矩形 的周长为 ,
∴ ,
设 ,则 , , ,,
故答案为 .
【点睛】
本题考查了矩形的性质,和列代数式及整式的化简,关键是读懂题目,列出代数式.
19.(1)1;(2)
【分析】
(1)先算绝对值,零指数幂,立方根和负整数指数幂,再算加减法,即可求解;
(2)先算分式的加法,再把除法化为乘法,进行约分,即可求解.
【详解】
解:(1)原式=
=1;
(2)原式=
=
= .
【点睛】
本题主要考查分式的混合运算以及实数的混合运算,掌握分式的通分和约分以及零指数幂
和负整数指数幂,是解题的关键.
20.(1) , ;(2)
【分析】
(1)根据分解因式法求解一元二次方程,即可得到答案;
(2)根据一元一次不等式组的性质计算,即可得到答案.
【详解】
(1)∵∴
∴ , ;
(2)∵
∴
∴
∴ .
【点睛】
本题考查了一元二次方程、一元一次不等式组的知识;解题的关键是熟练掌握一元二次方
程、一元一次不等式组的解法,从而完成求解.
21.(1)见解析;(2)见解析
【分析】
(1)由已知条件根据全的三角形的判定即可证明;
(2)首先根据平行四边形的判定证明四边形 是平行四边形,然后根据一组邻边相
等的平行四边形是菱形即可证明.
【详解】
解:(1)在 和 中,
∵ ,
∴ ;
(2)∵ 为 的直径,
∴ ,∵ ,
∴ , ,
∴ ∥ , ,
∴四边形 是平行四边形.
∵ ,
∴四边形 是菱形.
【点睛】
本题考查了全等三角形的判定及性质、菱形的判定、圆的基础知识,掌握全等三角形的判
定和特殊平行四边形的判定是解题的关键.
22.(1)见解析;(2)3
【分析】
(1)根据矩形的性质可得 ,则 ,因为折叠, ,
即可得证;
(2)设 用含 的代数式表示 ,由折叠, ,再用勾股定理求解即可
【详解】
(1) 四边形 是矩形
因为折叠,则
是等腰三角形
(2) 四边形 是矩形
,设 ,则
因为折叠,则 , ,
在 中
即
解得:
【点睛】
本题考查了矩形的性质,等腰三角形的判定定理,图像的折叠,勾股定理,熟悉以上知识
点是解题的关键.
23.50
【分析】
该商品打折卖出x件,找到等量关系即可.
【详解】
解:该商品打折卖出x件
解得x=8
经检验: 是原方程的解,且符合题意
∴商品打折前每件 元
答:该商品打折前每件50元.
【点睛】
此题考查分式方程实际问题中的销售问题,找到等量关系是解题的关键.
24.
【分析】
根据题意画出树状图,共有8种等可能的路径,其中落入③号槽内的有3种路径,再由概率公式求解即可.
【详解】
画树状图得:
所以圆球下落过程中共有8种路径,其中落入③号槽内的有3种,所以圆球落入③号槽内
的概率为 .
【点睛】
树状图法求概率的关键在于列举出所有可能的结果,当一个事件涉及三个或更多元素时,
为不重不漏地列出所有可能的结果,通常采用树状图法.
25.(1)7.6;(2)2020;(3)C;(4)C;(5)721
【分析】
(1)先把11个数据进行排序,再根据中位数的定定义,求解即可;
(2)先算出相邻两年增加的人数,进而即可得到答案;
(3)根据2021年与2020年中考人数的差,即可推出2022年中考人数;
(4)通过2019年中考,2021年中考, 2020年中考人数,即可得到答案;
(5)先算出2020年上半年学生人数,再根据比例求出求出2020年数学教师人数,进而即
可得到增加的教师人数.
【详解】
解:(1)∵11个数据从大到小排列:13.7,11.6,10.3,9.1,8.6,7.6,7.4,6.8,6.6,
6.2,6.1,
∴中位数为:7.6,
故答案是:7.6;
(2)∵6.6-6.1=0.5,7.4-6.6=0.8,9.1-7.4=1.7,11.6-9.1=2.5,13.7-11.6=2.1,
∴该市中考人数增加最多的年份是2020年,
故答案是:2020;
(3)∵2021年与2020年中考人数相差2.1万,∴2022年与2021年中考人数相差约2.1万,
∴2022年中考人数为15.3万人最合适,
故选C;
(4)∵2019年七年级同学在2021年中考,八年级同学在2020年中考,
∴2019年上半年,七八九年级总人数为:9.1+11.6+13.7=34.4(万)
故选C;
(5)由题意得:2020年上半年学生人数约为11.6+13.7+15.3=40.6,
∴ (人)
答:该市2020年上半年七、八、九三个年级的数学教师较上年同期增加721人.
【点睛】
本题主要考查折线统计图,中位数,通过折线统计图,准确提取数据,掌握中位数的定义,
是解题的关键.
26.(1)直线AB的解析式为: ;(2)6;(3)4
【分析】
(1)将 的横坐标分别代入 求出生意人y的值,得到A,B点坐标,再运用待
定系数法求出直线AB的解析式即可;
(2)求出OC的长,根据“ ”求解即可;
(3)分点P在直线AB的上方和下方两种情况根据分割法求解即可.
【详解】
解:(1)∵A,B是抛物线 上的两点,
∴当 时, ;当 时,
∴点A的坐标为(-2,1),点B的坐标为(4,4)
设直线AB的解析式为 ,把A,B点坐标代入得
解得,
所以,直线AB的解析式为: ;
(2)对于直线AB:
当 时,
∴
∴ = =6
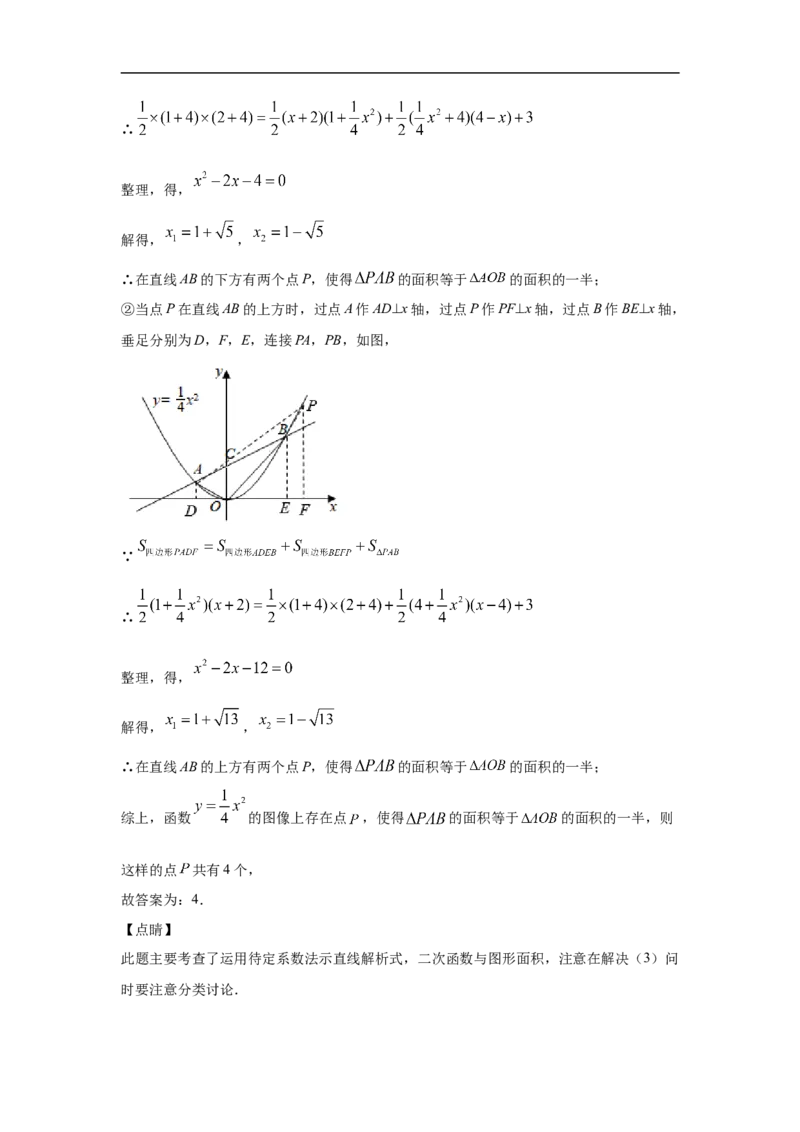
(3)设点P的坐标为( , )
∵ 的面积等于 的面积的一半,
∴ 的面积等于 =3,
①当点P在直线AB的下方时,过点A作AD⊥x轴,过点P作PF⊥x轴,过点B作BE⊥x轴,
垂足分别为D,F,E,连接PA,PB,如图,
∵∴
整理,得,
解得, ,
∴在直线AB的下方有两个点P,使得 的面积等于 的面积的一半;
②当点P在直线AB的上方时,过点A作AD⊥x轴,过点P作PF⊥x轴,过点B作BE⊥x轴,
垂足分别为D,F,E,连接PA,PB,如图,
∵
∴
整理,得,
解得, ,
∴在直线AB的上方有两个点P,使得 的面积等于 的面积的一半;
综上,函数 的图像上存在点 ,使得 的面积等于 的面积的一半,则
这样的点 共有4个,
故答案为:4.
【点睛】
此题主要考查了运用待定系数法示直线解析式,二次函数与图形面积,注意在解决(3)问
时要注意分类讨论.27.(1) ;(2)
【分析】
(1)解Rt△ADF求出AF,再解Rt△AEF求出AE即可;
(2)设DG交AB一直在点M,作AN⊥GD延长线于点N,解Rt△ADF求出DF,Rt△DFG
求出FG,得到AG,解Rt△AMN求出AM,根据AM-AE可求出结论.
【详解】
解:(1)在Rt△ADF中,
∴
=
=
=88cm
在Rt△AEF中,
∴
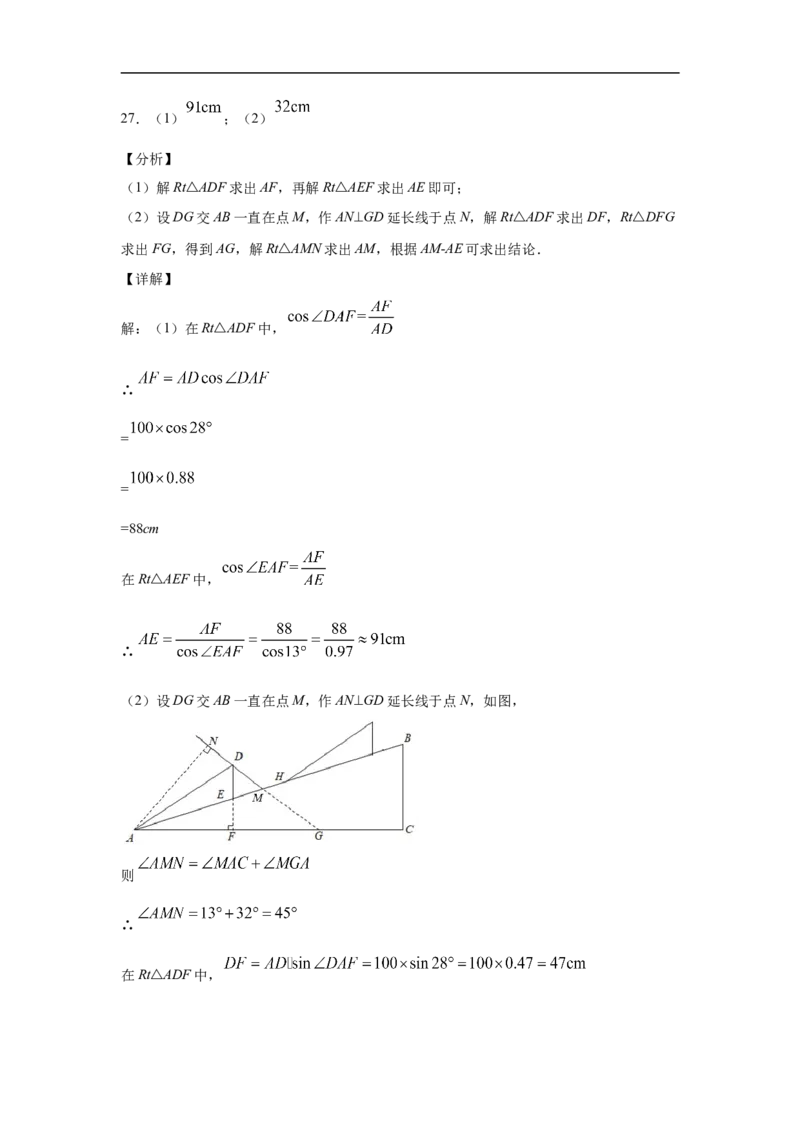
(2)设DG交AB一直在点M,作AN⊥GD延长线于点N,如图,
则
∴
在Rt△ADF中,在Rt△DFG中,
∴
∴AG=AF+FG=88+75.8=
∵AN⊥GD
∴∠ANG=90°
∴
在Rt△ANM中,
∴
∴
∴ 的最小值为
【点睛】
本题考查了解直角三角形的应用,解题的关键是构造直角三角形.
28.(1)①见详解;②见详解;(2)4≤MN<
【分析】
(1)①过点F作FG⊥AD交AD的延长线于点G,证明 ,即可得到结论;
②过点E作EH⊥DA交DA的延长线于点H,证明 ,结合 ,
可得GD=EH,同理:FG=AH,从而得 ,进而即可得到结论;
(2)过点F作FG⊥AD交AD的延长线于点G,过点E作EH⊥DA交DA的延长线于点H,可得∠AMD=90°,MN= EF,HG= 2AD=8,EH+FG= AD=4,然后求出当点P与点D重
合时, EF最大值= ,当点P与AD的中点重合时,EF最小值= HG=8,进而即可得到
答案.
【详解】
(1)①证明:过点F作FG⊥AD交AD的延长线于点G,
∵∠FPG+∠PFG=90°,∠FPG+∠CPD=90°,
∴∠FPG=∠CPD,
又∵∠PGF=∠CDP=90°,PC=PF,
∴ (AAS),
∴FG=PD,
∴ 的面积 ;
②过点E作EH⊥DA交DA的延长线于点H,
∵∠EPH+∠PEH=90°,∠EPH +∠BPA=90°,∴∠PEH =∠BPA,
又∵∠PHE=∠BAP=90°,PB=PE,
∴ (AAS),
∴EH=PA,
由①得:FG=PD,
∴EH+FG=PA+PD=AD=CD,
由①得: ,
∴PG=CD,
∴PD+GD= CD= EH+FG,
∴FG+ GD= EH+FG,
∴GD=EH,
同理:FG=AH,
又∵∠AHE=∠FGD,
∴ ,
∴ ;
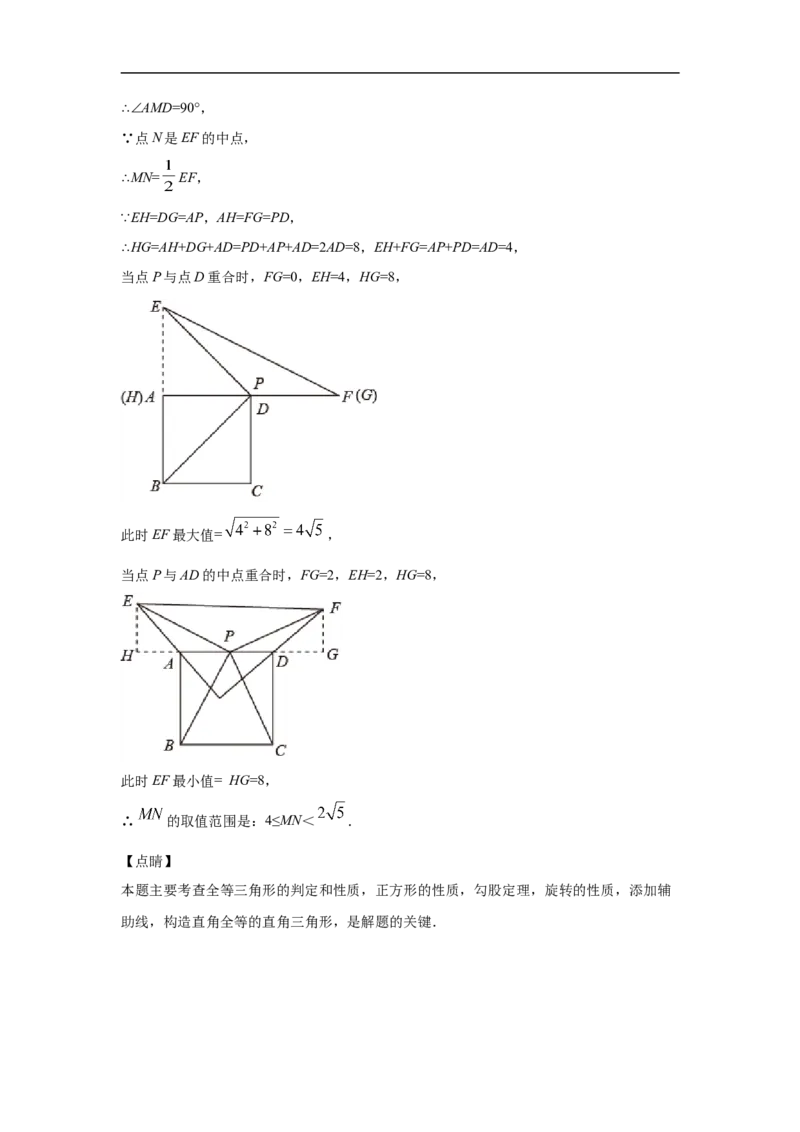
(2)过点F作FG⊥AD交AD的延长线于点G,过点E作EH⊥DA交DA的延长线于点H,
由(1)得: ,
∴∠HAE=∠GFD,
∵∠GFD+∠GDF=90°,
∴∠HAE+∠GDF=90°,
∵∠HAE=∠MAD,∠GDF=∠MDA,
∴∠MAD+∠MDA=90°,∴∠AMD=90°,
∵点N是EF的中点,
∴MN= EF,
∵EH=DG=AP,AH=FG=PD,
∴HG=AH+DG+AD=PD+AP+AD=2AD=8,EH+FG=AP+PD=AD=4,
当点P与点D重合时,FG=0,EH=4,HG=8,
此时EF最大值= ,
当点P与AD的中点重合时,FG=2,EH=2,HG=8,
此时EF最小值= HG=8,
∴ 的取值范围是:4≤MN< .
【点睛】
本题主要考查全等三角形的判定和性质,正方形的性质,勾股定理,旋转的性质,添加辅
助线,构造直角全等的直角三角形,是解题的关键.