文档内容
2021年甘肃省白银市中考数学试卷
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项。
1.(3分)3的倒数是( )
A.﹣3 B.3 C.﹣ D.
2.(3分)2021年是农历辛丑牛年,习近平总书记勉励全国各族人民在新的一年发扬“为
民服务孺子牛、创新发展拓荒牛、艰苦奋斗老黄牛”精神,某社区也开展了“迎新春牛
年剪纸展”,下面的剪纸作品是轴对称图形的是( )
A. B.
C. D.
3.(3分)下列运算正确的是( )
A. + =3 B.4 ﹣ =4 C. × = D. ÷ =4
4.(3分)中国疫苗撑起全球抗疫“生命线”!中国外交部数据显示,截至2021年3月底,
我国已无偿向80个国家和3个国际组织提供疫苗援助.预计2022年中国新冠疫苗产能
有望达到50亿剂,约占全球产能的一半,必将为全球抗疫作出重大贡献.数据“50
亿”用科学记数法表示为( )
A.5×108 B.5×109 C.5×1010 D.50×108
5.(3分)将直线y=5x向下平移2个单位长度,所得直线的表达式为( )
A.y=5x﹣2 B.y=5x+2 C.y=5(x+2) D.y=5(x﹣2)
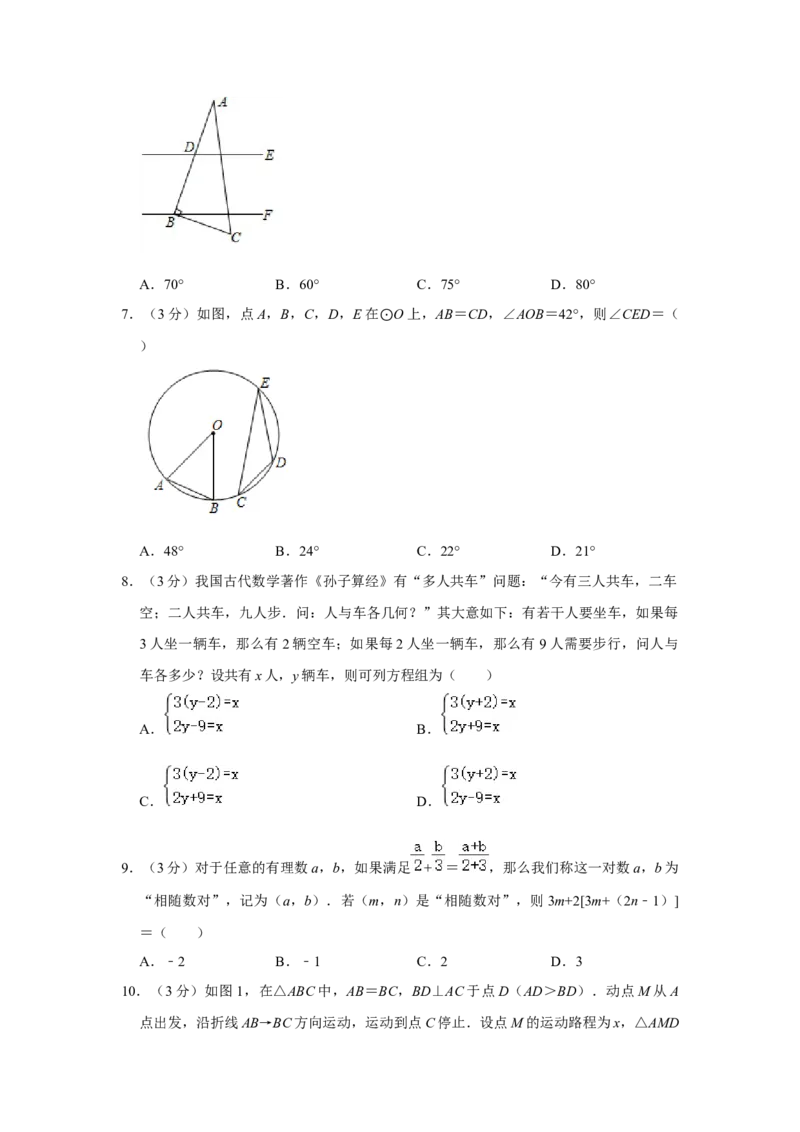
6.(3分)如图,直线DE∥BF,Rt△ABC的顶点B在BF上,若∠CBF=20°,则∠ADE
=( )A.70° B.60° C.75° D.80°
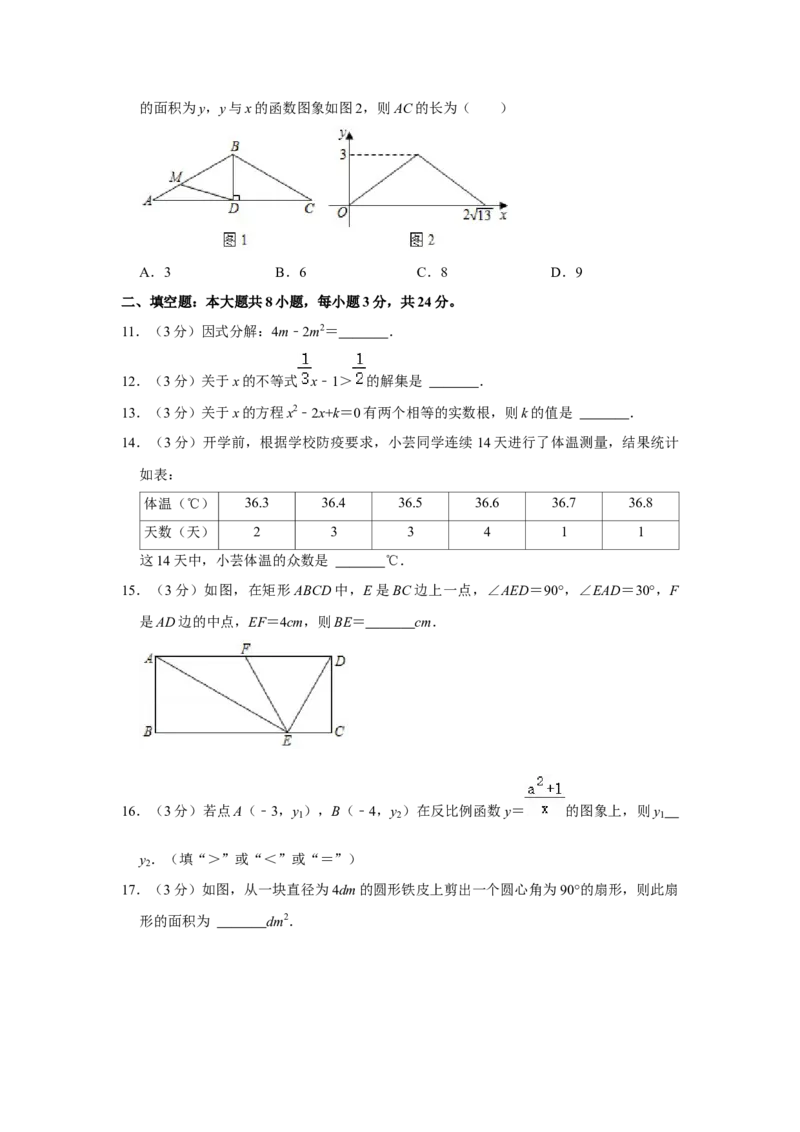
7.(3分)如图,点A,B,C,D,E在 O上,AB=CD,∠AOB=42°,则∠CED=(
) ⊙
A.48° B.24° C.22° D.21°
8.(3分)我国古代数学著作《孙子算经》有“多人共车”问题:“今有三人共车,二车
空;二人共车,九人步.问:人与车各几何?”其大意如下:有若干人要坐车,如果每
3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与
车各多少?设共有x人,y辆车,则可列方程组为( )
A. B.
C. D.
9.(3分)对于任意的有理数a,b,如果满足 + = ,那么我们称这一对数a,b为
“相随数对”,记为(a,b).若(m,n)是“相随数对”,则3m+2[3m+(2n﹣1)]
=( )
A.﹣2 B.﹣1 C.2 D.3
10.(3分)如图1,在△ABC中,AB=BC,BD⊥AC于点D(AD>BD).动点M从A
点出发,沿折线AB→BC方向运动,运动到点C停止.设点M的运动路程为x,△AMD的面积为y,y与x的函数图象如图2,则AC的长为( )
A.3 B.6 C.8 D.9
二、填空题:本大题共8小题,每小题3分,共24分。
11.(3分)因式分解:4m﹣2m2= .
12.(3分)关于x的不等式 x﹣1> 的解集是 .
13.(3分)关于x的方程x2﹣2x+k=0有两个相等的实数根,则k的值是 .
14.(3分)开学前,根据学校防疫要求,小芸同学连续14天进行了体温测量,结果统计
如表:
体温(℃) 36.3 36.4 36.5 36.6 36.7 36.8
天数(天) 2 3 3 4 1 1
这14天中,小芸体温的众数是 ℃.
15.(3分)如图,在矩形ABCD中,E是BC边上一点,∠AED=90°,∠EAD=30°,F
是AD边的中点,EF=4cm,则BE= cm.
16.(3分)若点A(﹣3,y ),B(﹣4,y )在反比例函数y= 的图象上,则y
1 2 1
y .(填“>”或“<”或“=”)
2
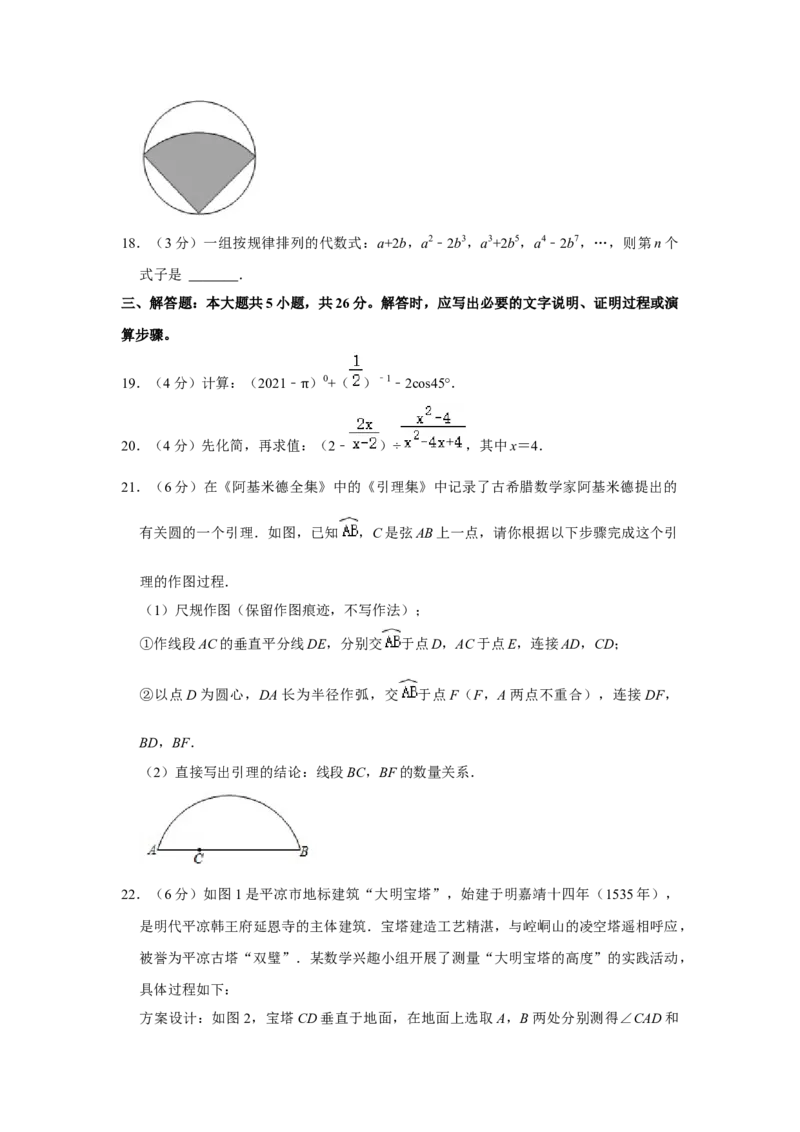
17.(3分)如图,从一块直径为4dm的圆形铁皮上剪出一个圆心角为90°的扇形,则此扇
形的面积为 dm2.18.(3分)一组按规律排列的代数式:a+2b,a2﹣2b3,a3+2b5,a4﹣2b7,…,则第n个
式子是 .
三、解答题:本大题共5小题,共26分。解答时,应写出必要的文字说明、证明过程或演
算步骤。
19.(4分)计算:(2021﹣ )0+( )﹣1﹣2cos45°.
π
20.(4分)先化简,再求值:(2﹣ )÷ ,其中x=4.
21.(6分)在《阿基米德全集》中的《引理集》中记录了古希腊数学家阿基米德提出的
有关圆的一个引理.如图,已知 ,C是弦AB上一点,请你根据以下步骤完成这个引
理的作图过程.
(1)尺规作图(保留作图痕迹,不写作法);
①作线段AC的垂直平分线DE,分别交 于点D,AC于点E,连接AD,CD;
②以点D为圆心,DA长为半径作弧,交 于点F(F,A两点不重合),连接DF,
BD,BF.
(2)直接写出引理的结论:线段BC,BF的数量关系.
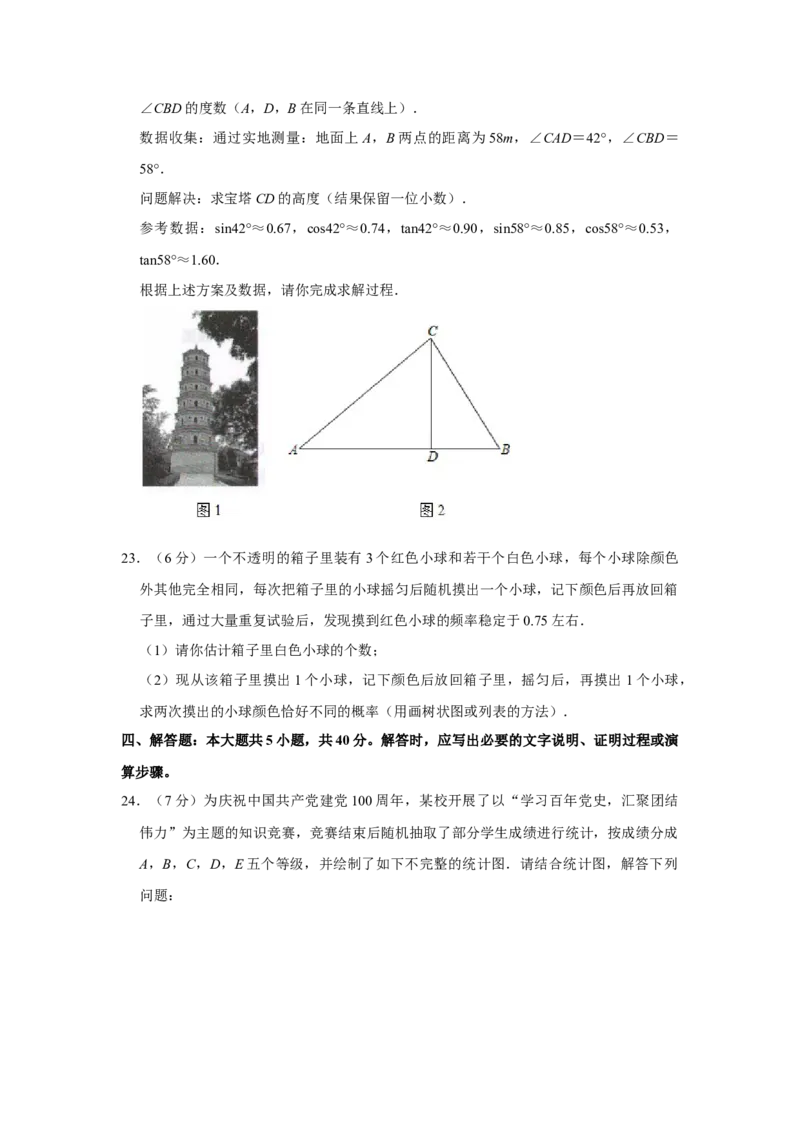
22.(6分)如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年(1535年),
是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,
被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,
具体过程如下:
方案设计:如图2,宝塔CD垂直于地面,在地面上选取A,B两处分别测得∠CAD和∠CBD的度数(A,D,B在同一条直线上).
数据收集:通过实地测量:地面上A,B两点的距离为58m,∠CAD=42°,∠CBD=
58°.
问题解决:求宝塔CD的高度(结果保留一位小数).
参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin58°≈0.85,cos58°≈0.53,
tan58°≈1.60.
根据上述方案及数据,请你完成求解过程.
23.(6分)一个不透明的箱子里装有3个红色小球和若干个白色小球,每个小球除颜色
外其他完全相同,每次把箱子里的小球摇匀后随机摸出一个小球,记下颜色后再放回箱
子里,通过大量重复试验后,发现摸到红色小球的频率稳定于0.75左右.
(1)请你估计箱子里白色小球的个数;
(2)现从该箱子里摸出1个小球,记下颜色后放回箱子里,摇匀后,再摸出1个小球,
求两次摸出的小球颜色恰好不同的概率(用画树状图或列表的方法).
四、解答题:本大题共5小题,共40分。解答时,应写出必要的文字说明、证明过程或演
算步骤。
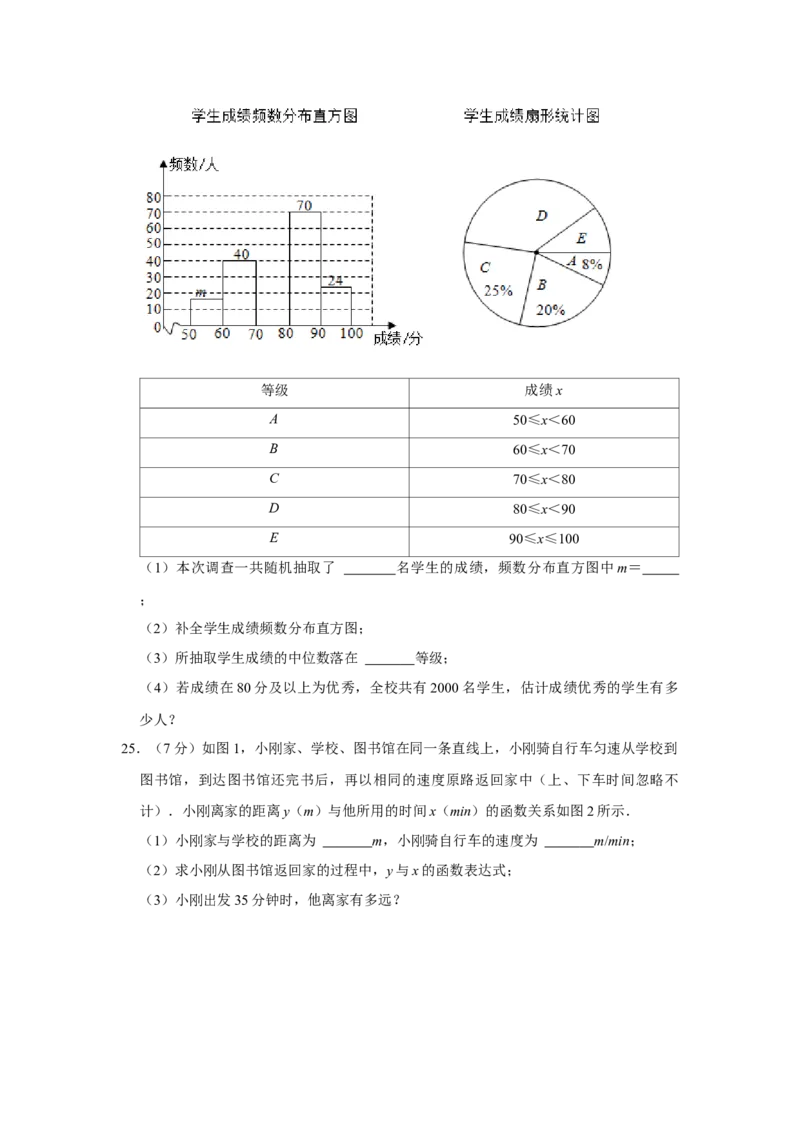
24.(7分)为庆祝中国共产党建党100周年,某校开展了以“学习百年党史,汇聚团结
伟力”为主题的知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分成
A,B,C,D,E五个等级,并绘制了如下不完整的统计图.请结合统计图,解答下列
问题:等级 成绩x
A 50≤x<60
B 60≤x<70
C 70≤x<80
D 80≤x<90
E 90≤x≤100
(1)本次调查一共随机抽取了 名学生的成绩,频数分布直方图中m=
;
(2)补全学生成绩频数分布直方图;
(3)所抽取学生成绩的中位数落在 等级;
(4)若成绩在80分及以上为优秀,全校共有2000名学生,估计成绩优秀的学生有多
少人?
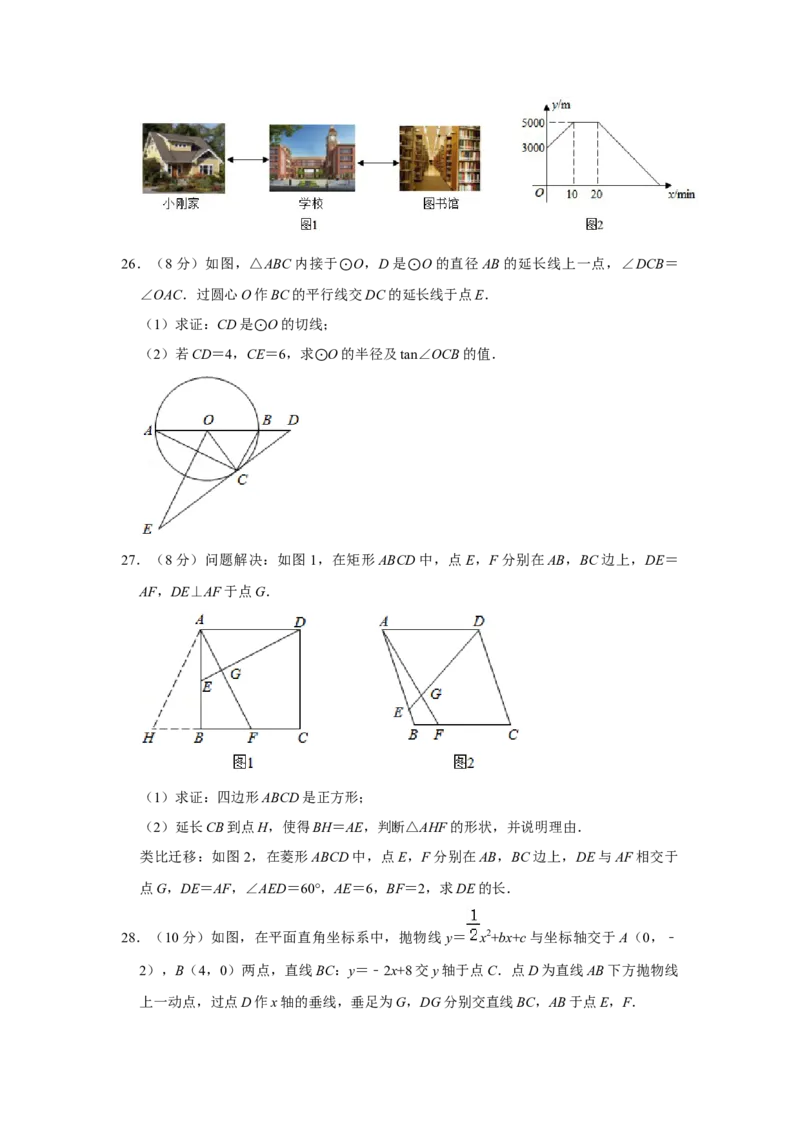
25.(7分)如图1,小刚家、学校、图书馆在同一条直线上,小刚骑自行车匀速从学校到
图书馆,到达图书馆还完书后,再以相同的速度原路返回家中(上、下车时间忽略不
计).小刚离家的距离y(m)与他所用的时间x(min)的函数关系如图2所示.
(1)小刚家与学校的距离为 m,小刚骑自行车的速度为 m/min;
(2)求小刚从图书馆返回家的过程中,y与x的函数表达式;
(3)小刚出发35分钟时,他离家有多远?26.(8分)如图,△ABC内接于 O,D是 O的直径AB的延长线上一点,∠DCB=
∠OAC.过圆心O作BC的平行线⊙交DC的延⊙长线于点E.
(1)求证:CD是 O的切线;
(2)若CD=4,C⊙E=6,求 O的半径及tan∠OCB的值.
⊙
27.(8分)问题解决:如图1,在矩形ABCD中,点E,F分别在AB,BC边上,DE=
AF,DE⊥AF于点G.
(1)求证:四边形ABCD是正方形;
(2)延长CB到点H,使得BH=AE,判断△AHF的形状,并说明理由.
类比迁移:如图2,在菱形ABCD中,点E,F分别在AB,BC边上,DE与AF相交于
点G,DE=AF,∠AED=60°,AE=6,BF=2,求DE的长.
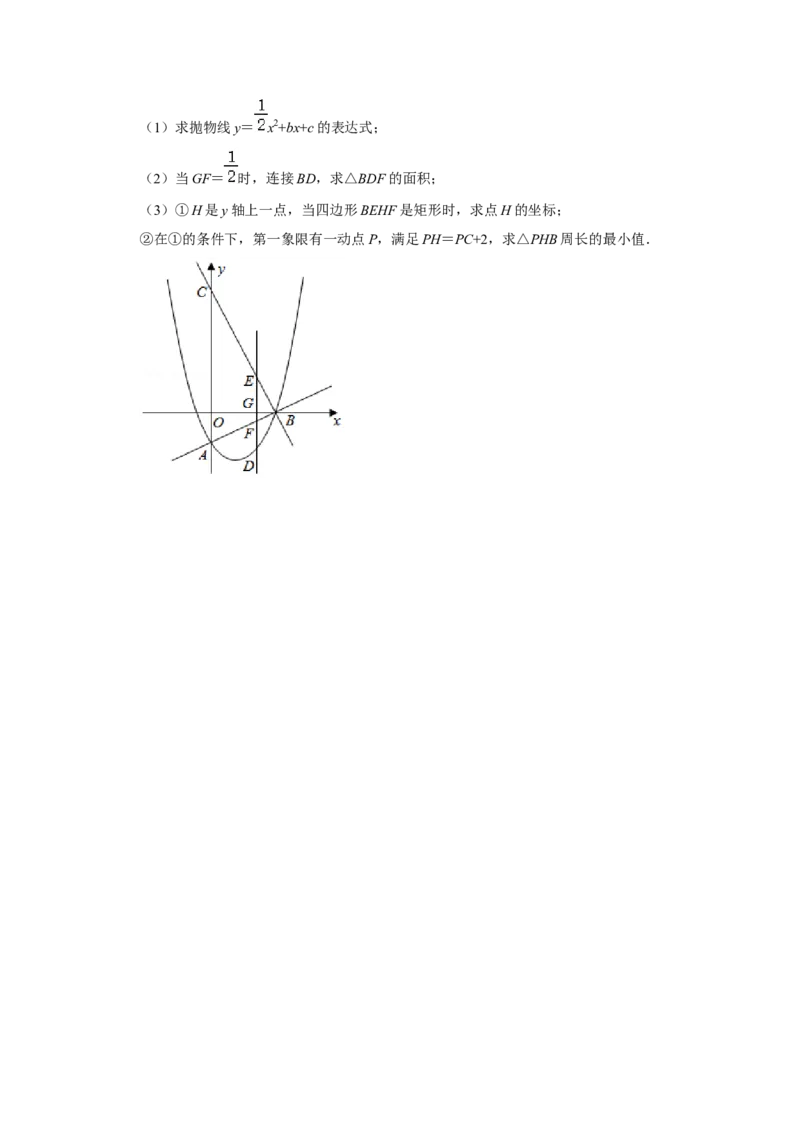
28.(10分)如图,在平面直角坐标系中,抛物线 y= x2+bx+c与坐标轴交于A(0,﹣
2),B(4,0)两点,直线BC:y=﹣2x+8交y轴于点C.点D为直线AB下方抛物线
上一动点,过点D作x轴的垂线,垂足为G,DG分别交直线BC,AB于点E,F.(1)求抛物线y= x2+bx+c的表达式;
(2)当GF= 时,连接BD,求△BDF的面积;
(3)①H是y轴上一点,当四边形BEHF是矩形时,求点H的坐标;
②在①的条件下,第一象限有一动点P,满足PH=PC+2,求△PHB周长的最小值.