文档内容
2022 年江苏省淮安市中考数学试卷
参考答案
一、选择题(本大题共 8小题,每小题 3分,共 24分.)
1.(3分)-2 的相反数是( )
1 1
A.2 B.-2 C.- D.
2 2
答案:A
解析::-2的相反数是:-(-2)=2,
故选:A.
2.(3分)计算a2•a3的结果是( )
A.a2 B.a3 C.a5 D.a6
答案:C
解析:a2•a3=a5.
故选:C.
3.(3分)2022 年十三届全国人大五次会议审议通过的政府工作报告中提出,
今年城镇新增就业目标为 11000000人以上.数据 11000000用科学记数法表示应
为( )
A.0.11×108 B.1.1×107
C.11×106 D.1.1×106
答案:B
解析:11000000=1.1×107.
故选:B.
4.(3分)某公司对 25名营销人员4月份销售某种商品的情况统计如下:
则这 25名营销人员销售量的众数是( )
A.50 B.40 C.35 D.30
答案:D
10 |解析:因为销售量为 30 件出现的次数最多,所以这 25名营销人员销售量的
众数是30.
故选:D.
5.(3分)下列长度的三条线段能组成三角形的是( )
A.3,3,6 B.3,5,10 C.4,6,9 D.4,5,9
答案:C
解析:A、∵3+3=6,
∴长度为 3,3,6的三条线段不能组成三角形,本选项不符合题意;
B、∵3+5<10,
∴长度为 3,5,10的三条线段不能组成三角形,本选项不符合题意;
C、∵4+6>9,
∴长度为 4,6,9的三条线段能组成三角形,本选项符合题意;
D、∵4+5=9,
∴长度为 4,5,9的三条线段不能组成三角形,本选项不符合题意;
故选:C.
6.(3分)若关于 x的一元二次方程x2-2x-k=0没有实数根,则 k的值可
以是( )
A.-2 B.-1 C.0 D.1
答案:A
解析:∵一元二次方程x2-2x-k=0没有实数根,
∴Δ=(−2)2−4×1×(−k) = 4+4k<0,
∴k<-1,
故选:A.
7.(3分)如图,四边形 ABCD 是⊙O的内接四边形,若∠AOC=160°,则∠
ABC的度数是( )
11 |A.80° B.100° C.140° D.160°
答案:B
解析:∵∠AOC=160°,
1
∴∠ADC= ∠AOC=80°,
2
∵四边形 ABCD 是⊙O的内接四边形,
∴∠ABC=180°-∠ADC=180°-80°=100°,
故选:B.
8.(3 分)如图,在△ABC 中,AB=AC,∠BAC 的平分线交 BC 于点 D,E 为
AC的中点,若 AB=10,则DE的长是( )
A.8 B.6 C.5 D.4
答案:C
解析:∵AB=AC=10,AD平分∠BAC,
∴AD⊥BC,
∴∠ADC=90°,
∵E 为AC的中点,
1
∴DE= AC=5,
2
故选:C.
二、填空题(本大题共 8小题,每小题 3分,共 24分)
9.(3分)实数 27的立方根是 .
12 |答案:3
解析:∵3的立方等于27,
∴27 的立方根等于 3.
故答案为 3.
10.(3分)五边形的内角和是 °.
答案:540
解析:根据题意得:(5-2)•180°=540°,
故答案为:540°.
3
11.(3分)方程 -1=0的解是 .
x−2
答案:x=5
3
解析: -1=0
x−2
方程两边都乘 x-2,得3-(x-2)=0,
解得:x=5,
检验:当 x=5 时,x-2≠0,
所以 x=5是原方程的解,
即原方程的解是 x=5,
故答案为:x=5.
12.(3分)一组数据 3、-2、4、1、4 的平均数是 .
答案:2
3−2+4+1+4
解析:数据3、-2、4、1、4的平均数是: = 2
5
故答案为:2.
13.(3分)如图,在▱ABCD 中,CA⊥AB,若∠B=50°,则∠CAD的度数是 .
答案:40°
解析:∵四边形 ABCD是平行四边形,
∴AD∥BC,
13 |∴∠CAD=∠ACB,
∵CA⊥AB,
∴∠BAC=90°,
∵∠B=50°,
∴∠ACB=90°-∠B=40°,
∴∠CAD=∠ACB=40°,
故答案为:40°.
14.(3 分)若圆锥的底面圆半径为 2,母线长为 5,则该圆锥的侧面积
是 .(结果保留π)
答案:10π
解析:根据圆锥的侧面积公式:πrl=π×2×5=10π,
故答案为:10π.
15.(3分)在平面直角坐标系中,将点 A(2,3)向下平移5个单位长度得
k
到点B,若点 B恰好在反比例函数 y= 的图像上,则 k的值是 .
x
答案:-4
解析:将点A(2,3)向下平移5个单位长度得到点 B,则B(2,-2),
k
∵点 B恰好在反比例函数 y= 的图像上,
x
∴k=2×(-2)=-4,
故答案为:-4.
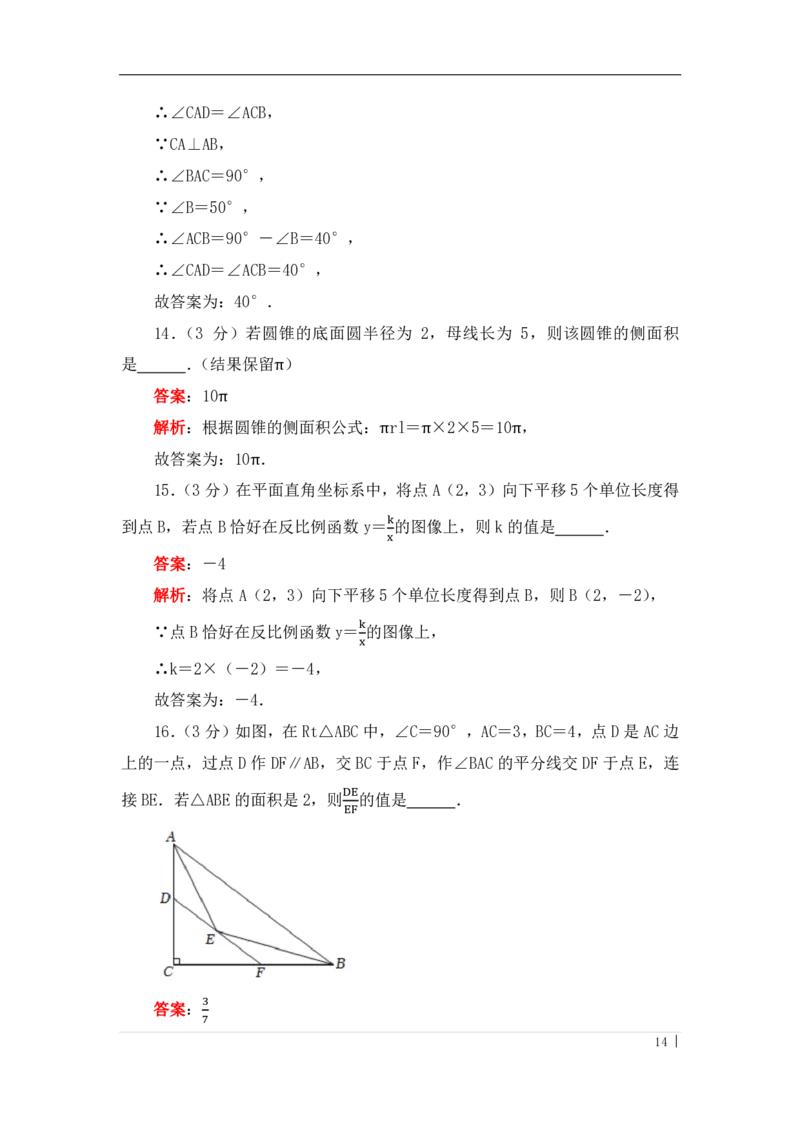
16.(3分)如图,在 Rt△ABC中,∠C=90°,AC=3,BC=4,点 D是AC边
上的一点,过点 D 作 DF∥AB,交 BC 于点 F,作∠BAC 的平分线交 DF 于点 E,连
DE
接BE.若△ABE的面积是 2,则 的值是 .
EF
3
答案:
7
14 |解析:在Rt△ABC中,由勾股定理得,AB=5,
∵△ABE的面积是 2,
4
∴点 E到AB的距离为 ,
5
AC•BC 12
在 Rt△ABC中,点 C到AB的距离为 = ,
AB 5
8
∴点 C到DF的距离为 ,
5
∵DF∥AB,
CD 2 DF
∴ = = ,
CA 3 AB
10
∴CD=2,DF= ,
3
∵AE 平分∠CAB,
∴∠BAE=∠CAE,
∵DF∥AB,
∴∠AED=∠BAE,
∴∠DAE=∠DEA,
∴DA=DE=1,
10 7
∴EF=DF-DE= -1= ,
3 3
DE 3
∴ = ,
EF 7
3
故答案为: .
7
三、解答题(本大题共 11 小题,共 102 分.)
17.(10分)(1)计算:|−5|+(3-√2)0-2tan45°;
a 3
(2)化简: ÷(1+ )
a2−9 a−3
解答:(1)原式=5+1-2×1
=5+1-2
=4;
a a
(2)原式= ÷
(a+3)(a−3) a−3
a a−3
= ×
(a+3)(a−3) a
15 |1
=
a+3
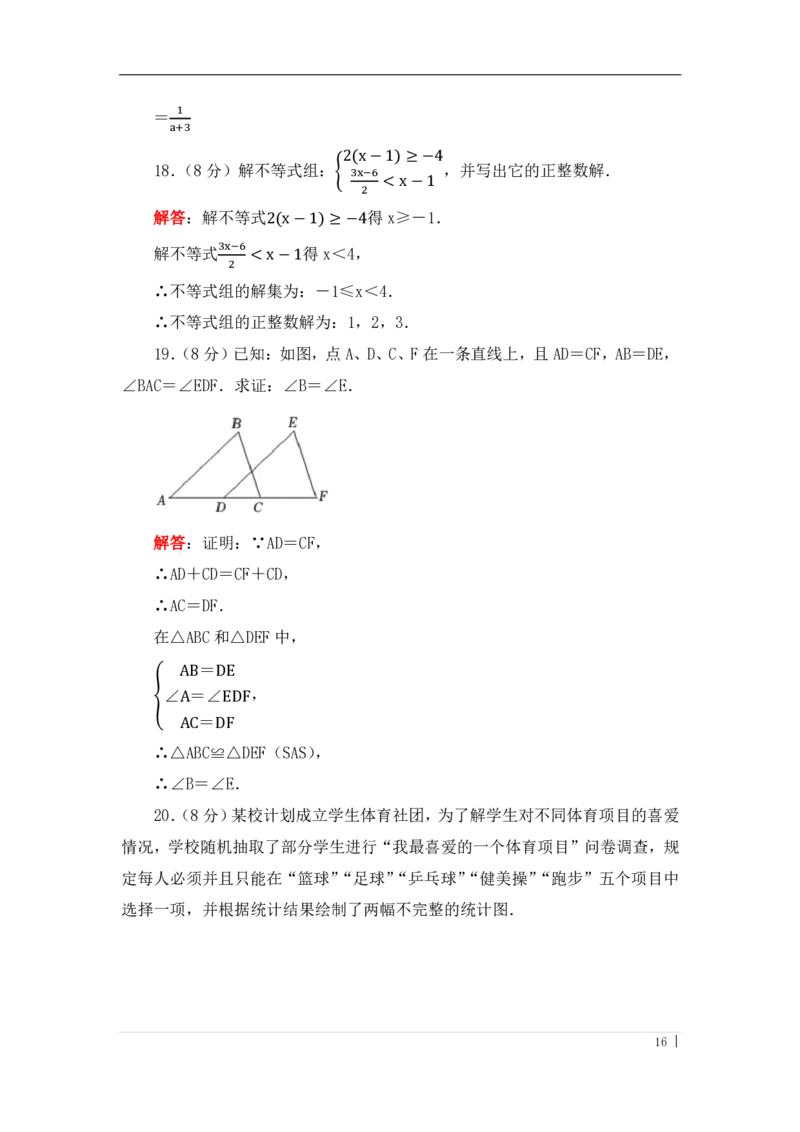
2(x−1) ≥ −4
18.(8分)解不等式组:{
3x−6
,并写出它的正整数解.
< x−1
2
解答:解不等式2(x−1) ≥ −4得x≥-1.
3x−6
解不等式 < x−1得x<4,
2
∴不等式组的解集为:-1≤x<4.
∴不等式组的正整数解为:1,2,3.
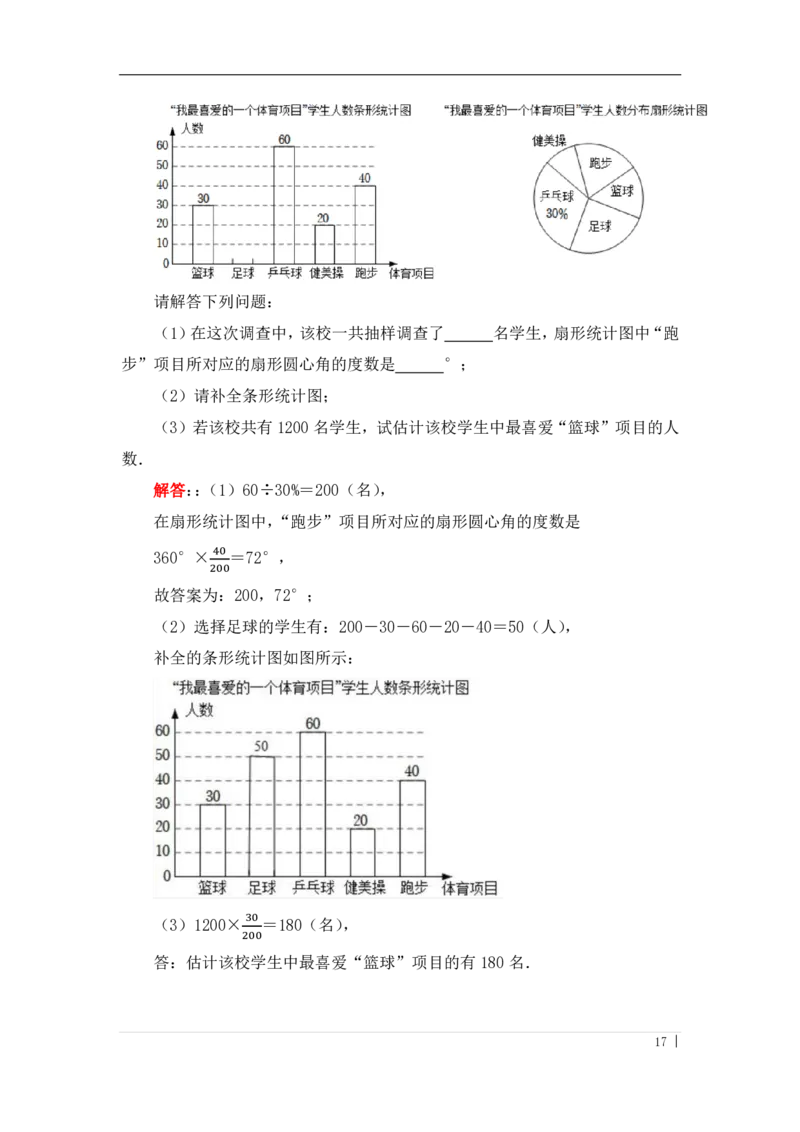
19.(8分)已知:如图,点 A、D、C、F 在一条直线上,且AD=CF,AB=DE,
∠BAC=∠EDF.求证:∠B=∠E.
解答:证明:∵AD=CF,
∴AD+CD=CF+CD,
∴AC=DF.
在△ABC和△DEF 中,
AB=DE
{∠A=∠EDF,
AC=DF
∴△ABC≌△DEF(SAS),
∴∠B=∠E.
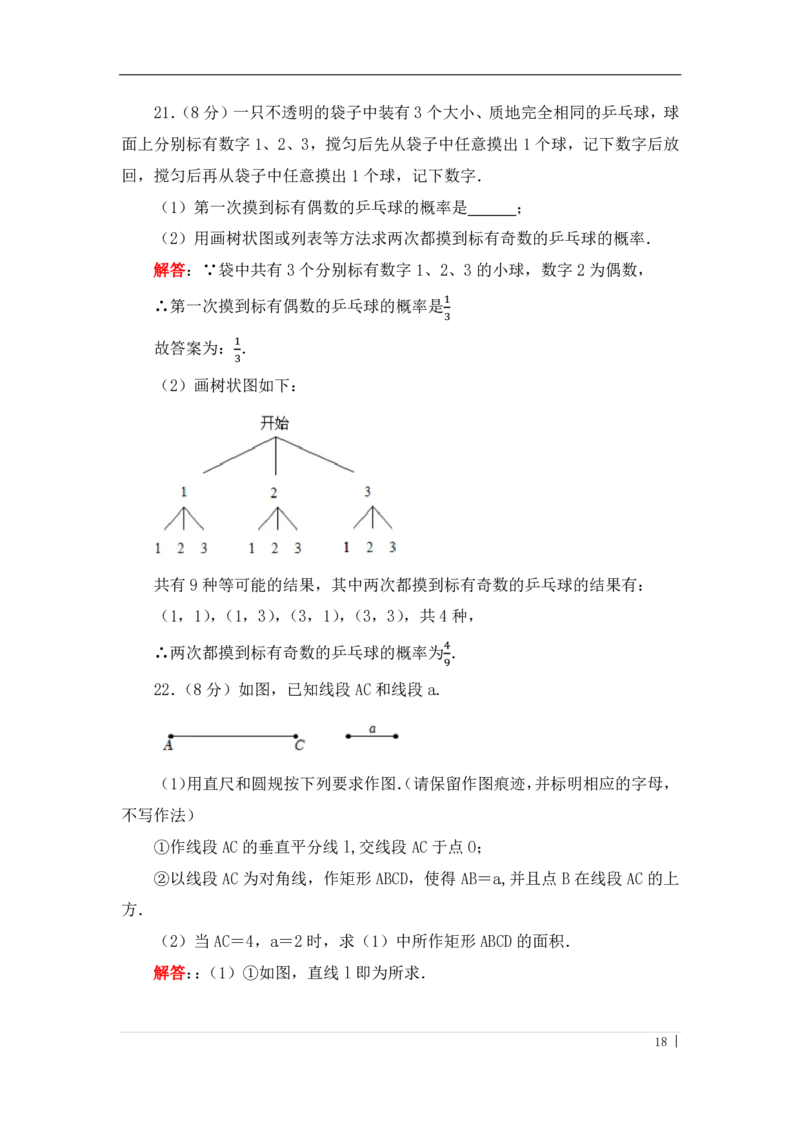
20.(8分)某校计划成立学生体育社团,为了解学生对不同体育项目的喜爱
情况,学校随机抽取了部分学生进行“我最喜爱的一个体育项目”问卷调查,规
定每人必须并且只能在“篮球”“足球”“乒乓球”“健美操”“跑步”五个项目中
选择一项,并根据统计结果绘制了两幅不完整的统计图.
16 |请解答下列问题:
(1)在这次调查中,该校一共抽样调查了 名学生,扇形统计图中“跑
步”项目所对应的扇形圆心角的度数是 °;
(2)请补全条形统计图;
(3)若该校共有 1200名学生,试估计该校学生中最喜爱“篮球”项目的人
数.
解答::(1)60÷30%=200(名),
在扇形统计图中,“跑步”项目所对应的扇形圆心角的度数是
40
360°× =72°,
200
故答案为:200,72°;
(2)选择足球的学生有:200-30-60-20-40=50(人),
补全的条形统计图如图所示:
30
(3)1200× =180(名),
200
答:估计该校学生中最喜爱“篮球”项目的有 180名.
17 |21.(8分)一只不透明的袋子中装有 3 个大小、质地完全相同的乒乓球,球
面上分别标有数字 1、2、3,搅匀后先从袋子中任意摸出 1个球,记下数字后放
回,搅匀后再从袋子中任意摸出 1个球,记下数字.
(1)第一次摸到标有偶数的乒乓球的概率是 ;
(2)用画树状图或列表等方法求两次都摸到标有奇数的乒乓球的概率.
解答:∵袋中共有 3个分别标有数字 1、2、3的小球,数字2为偶数,
1
∴第一次摸到标有偶数的乒乓球的概率是
3
1
故答案为: .
3
(2)画树状图如下:
共有 9种等可能的结果,其中两次都摸到标有奇数的乒乓球的结果有:
(1,1),(1,3),(3,1),(3,3),共 4种,
4
∴两次都摸到标有奇数的乒乓球的概率为 .
9
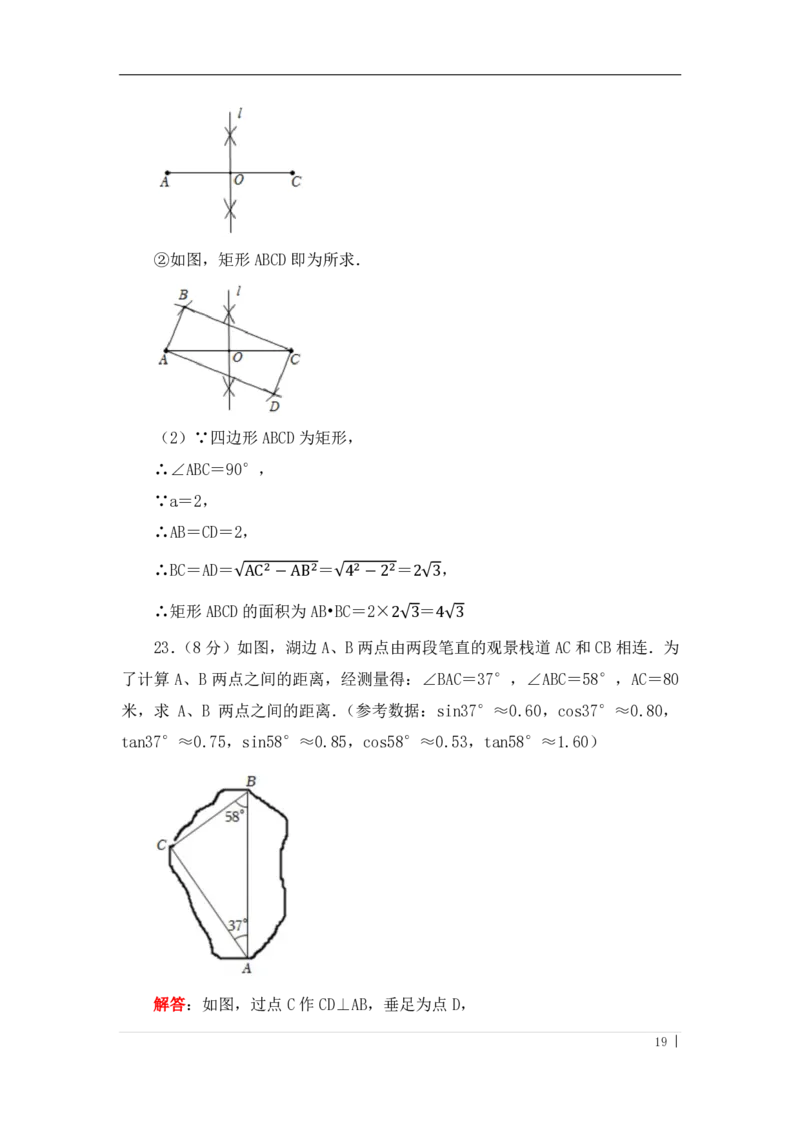
22.(8分)如图,已知线段 AC和线段 a.
(1)用直尺和圆规按下列要求作图.(请保留作图痕迹,并标明相应的字母,
不写作法)
①作线段 AC的垂直平分线 l,交线段AC 于点O;
②以线段 AC 为对角线,作矩形 ABCD,使得 AB=a,并且点 B 在线段 AC 的上
方.
(2)当AC=4,a=2时,求(1)中所作矩形 ABCD的面积.
解答::(1)①如图,直线 l 即为所求.
18 |②如图,矩形 ABCD即为所求.
(2)∵四边形 ABCD为矩形,
∴∠ABC=90°,
∵a=2,
∴AB=CD=2,
∴BC=AD=√AC2 −AB2=√42 −22=2√3,
∴矩形 ABCD的面积为 AB•BC=2×2√3=4√3
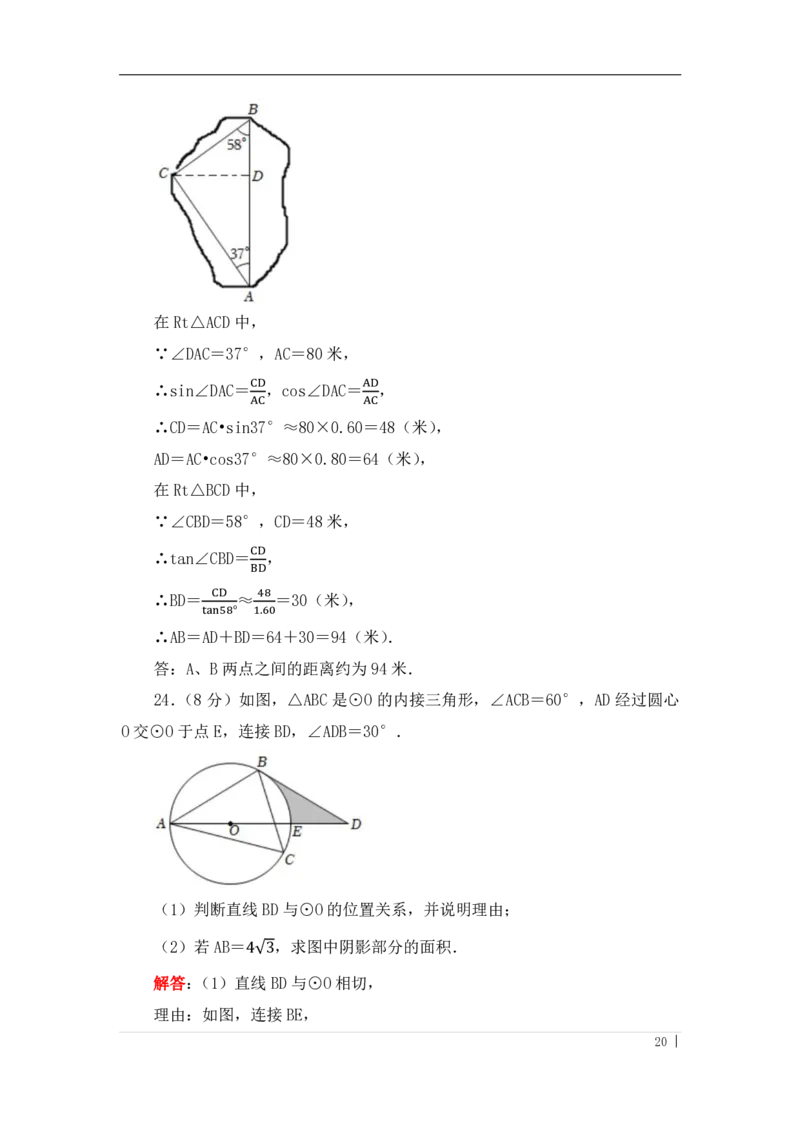
23.(8分)如图,湖边 A、B两点由两段笔直的观景栈道 AC和 CB相连.为
了计算 A、B 两点之间的距离,经测量得:∠BAC=37°,∠ABC=58°,AC=80
米,求 A、B 两点之间的距离.(参考数据:sin37°≈0.60,cos37°≈0.80,
tan37°≈0.75,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
解答:如图,过点 C作CD⊥AB,垂足为点 D,
19 |在 Rt△ACD中,
∵∠DAC=37°,AC=80米,
CD AD
∴sin∠DAC= ,cos∠DAC= ,
AC AC
∴CD=AC•sin37°≈80×0.60=48(米),
AD=AC•cos37°≈80×0.80=64(米),
在 Rt△BCD中,
∵∠CBD=58°,CD=48米,
CD
∴tan∠CBD= ,
BD
CD 48
∴BD= ≈ =30(米),
tan58° 1.60
∴AB=AD+BD=64+30=94(米).
答:A、B两点之间的距离约为 94米.
24.(8 分)如图,△ABC 是⊙O 的内接三角形,∠ACB=60°,AD 经过圆心
O交⊙O 于点E,连接 BD,∠ADB=30°.
(1)判断直线 BD与⊙O的位置关系,并说明理由;
(2)若AB=4√3,求图中阴影部分的面积.
解答:(1)直线 BD与⊙O相切,
理由:如图,连接 BE,
20 |∵∠ACB=60°,
∴∠AEB=∠C=60°,
连接 OB,
∵OB=OC,
∴△OBE是等边三角形,
∴∠BOD=60°,
∵∠ADB=30°,
∴∠OBD=180°-60°-30°=90°,
∴OB⊥BD,
∵OB 是⊙O的半径,
∴直线 BD与⊙O相切;
(2)∵AE是⊙O的直径,
∴∠ABE=90°,
∵AB=4√3,
∴sin∠AEB=sin60°=
AB
=
4√3 =√3
,
AE AE 2
∴AE=8,
∴OB=4,
∴BD=√3OB=4√3,
1 60𝜋×42 8π
∴图中阴影部分的面积=S -S = ×4×4√3- =8√3-
△OBD 扇形BOE 2 360 3
25.(10分)端午节前夕,某超市从厂家分两次购进 A、B两种品牌的粽子,
两次进货时,两种品牌粽子的进价不变.第一次购进 A品牌粽子100 袋和B品牌
粽子150 袋,总费用为 7000元;第二次购进 A品牌粽子180袋和B品牌粽子 120
袋,总费用为8100 元.
21 |(1)求A、B两种品牌粽子每袋的进价各是多少元;
(2)当 B 品牌粽子销售价为每袋 54 元时,每天可售出 20 袋,为了促销,
该超市决定对B品牌粽子进行降价销售.经市场调研,若每袋的销售价每降低 1
元,则每天的销售量将增加 5袋.当B品牌粽子每袋的销售价降低多少元时,每
天售出B品牌粽子所获得的利润最大?最大利润是多少元?
解答::(1)A 种品牌粽子每袋的进价是 x元,B种品牌粽子每袋的进价是 y
元,
100x+150y=7000
根据题意得,{
180x+120y=8100
x=25
解得{
y=30
答:A种品牌粽子每袋的进价是 25元,B种品牌粽子每袋的进价是 30元;
(2)设 B 品牌粽子每袋的销售价降低 a 元时,每天售出 B 品牌粽子所获得
的利润最大,利润为 w元,
根据题意得,
w=(54−a−30)(20+5a) = −5a2 +100a+480 = −5(a−10)2 +980,
∵-5<0,
∴当 B 品牌粽子每袋的销售价降低 10 元时,每天售出 B 品牌粽子所获得的
利润最大,最大利润是 980元.
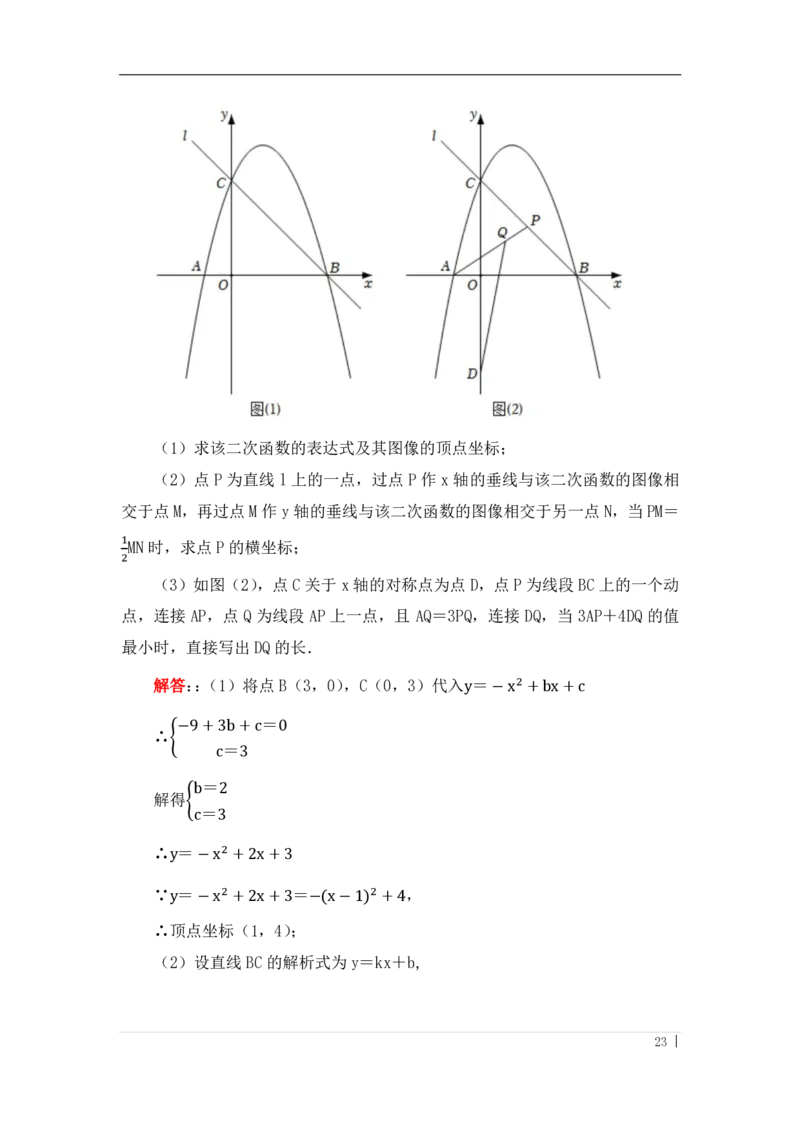
26.(12 分)如图(1),二次函数y=−x2 +bx+c的图像与 x 轴交于 A、B
两点,与y轴交于 C点,点B的坐标为(3,0),点C的坐标为(0,3),直线l
经过B、C两点.
22 |(1)求该二次函数的表达式及其图像的顶点坐标;
(2)点 P 为直线 l 上的一点,过点 P 作 x 轴的垂线与该二次函数的图像相
交于点M,再过点M 作y轴的垂线与该二次函数的图像相交于另一点 N,当PM=
1
MN时,求点P的横坐标;
2
(3)如图(2),点 C 关于x轴的对称点为点 D,点P为线段BC 上的一个动
点,连接 AP,点 Q 为线段 AP 上一点,且 AQ=3PQ,连接 DQ,当 3AP+4DQ 的值
最小时,直接写出 DQ的长.
解答::(1)将点 B(3,0),C(0,3)代入y=−x2 +bx+c
−9+3b+c=0
∴{
c=3
b=2
解得{
c=3
∴y=−x2 +2x+3
∵y=−x2 +2x+3=−(x−1)2 +4,
∴顶点坐标(1,4);
(2)设直线BC 的解析式为y=kx+b,
23 |3k+b=0
∴{
b=3
k=−1
解得{
b=3
∴y=-x+3,
设 P(t,-t+3),则M(t,-t2+2t+3),N(2-t,-t2+2t+3),
∴PM=|t2-3t|,MN=|2-2t|,
1
∵PM= MN,
2
∴|t2-3t|= 1 |2-2t|,
2
解得 t=1+√2或1-√2或t=2+√3或 2-√3
∴P 点横坐标为 1+√2或1-√2或2+√3或2-√3;
(3)∵C(0,3),D点与C点关于x轴对称,
∴D(0,-3),
令 y=0,则−x2 +2x+3 = 0,
解得 x=-1或 x=3,
∴A(-1,0),
∴AB=4,
∵AQ=3PQ,
∴Q 点在平行于 BC的线段上,设此线段与 x轴的交点为G,
∴QG∥BC,
AQ AG
∴ = ,
AP BA
3 AG
∴ = ,
4 4
∴AG=3,
∴G(2,0),
∵OB=OC,
∴∠OBC=45°,
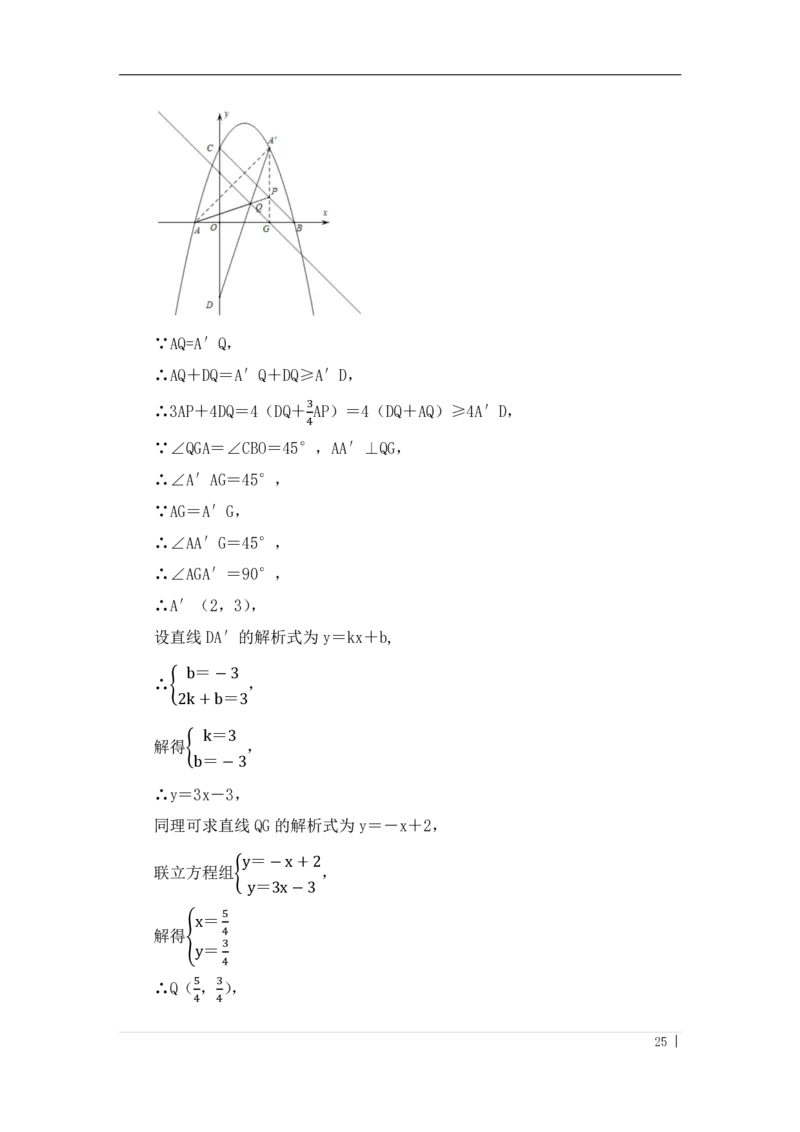
作 A点关于GQ 的对称点A′,连接AD 与AP交于点Q,
24 |∵AQ=A′Q,
∴AQ+DQ=A′Q+DQ≥A′D,
3
∴3AP+4DQ=4(DQ+ AP)=4(DQ+AQ)≥4A′D,
4
∵∠QGA=∠CBO=45°,AA′⊥QG,
∴∠A′AG=45°,
∵AG=A′G,
∴∠AA′G=45°,
∴∠AGA′=90°,
∴A′(2,3),
设直线 DA′的解析式为 y=kx+b,
b=−3
∴{ ,
2k+b=3
k=3
解得{ ,
b=−3
∴y=3x-3,
同理可求直线 QG的解析式为y=-x+2,
y=−x+2
联立方程组{ ,
y=3x−3
5
x=
解得{ 4
3
y=
4
5 3
∴Q( , ),
4 4
25 |∴DQ=
5√10
.
4
27.(14 分)在数学兴趣小组活动中,同学们对菱形的折叠问题进行了探
究.如图(1),在菱形 ABCD中,∠B为锐角,E为BC中点,连接DE,将菱形 ABCD
沿 DE 折叠,得到四边形 A′B′ED,点 A 的对应点为点 A′,点 B 的对应点为点
B′.
【观察发现】
A′D与B′E的位置关系是 ;
【思考表达】
(1)连接B′C,判断∠DEC与∠B′CE 是否相等,并说明理由;
(2)如图(2),延长 DC 交 A′B′于点 G,连接 EG,请探究∠DEG 的度数,
并说明理由;
【综合运用】
如图(3),当∠B=60°时,连接B′C,延长 DC交A′B′于点G,连接 EG,
请写出B′C、EG、DG之间的数量关系,并说明理由.
解答::【观察发现】如图(1)中,由翻折的性质可知,A′D∥B′E.
故答案为:A′D∥B′E;
【思考表达】(1)结论:∠DEC=∠B′CE.
理由:如图(2)中,连接BB′.
∵EB=EC=EB′,
∴∠BB′C=90°,
∴BB′⊥B′C,
由翻折变换的性质可知 BB′⊥DE,
26 |∴DE∥CB′,
∴∠DEC=∠C=∠B′CE;
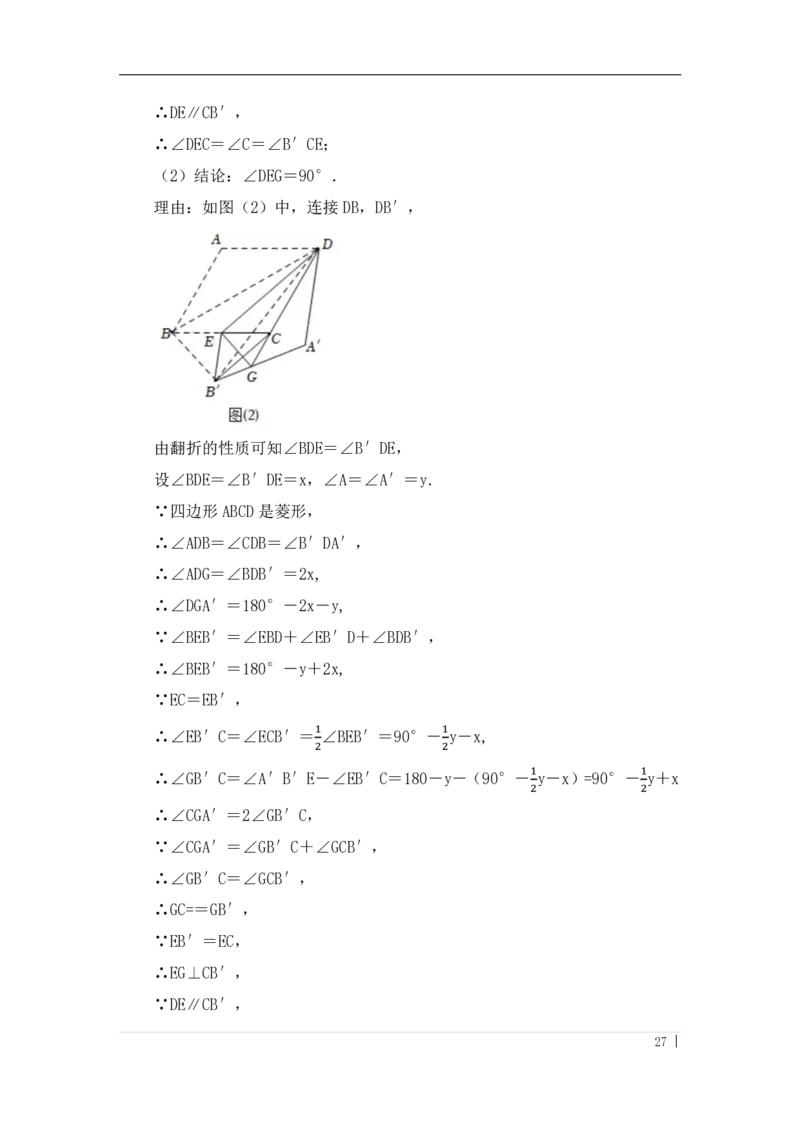
(2)结论:∠DEG=90°.
理由:如图(2)中,连接DB,DB′,
由翻折的性质可知∠BDE=∠B′DE,
设∠BDE=∠B′DE=x,∠A=∠A′=y.
∵四边形 ABCD 是菱形,
∴∠ADB=∠CDB=∠B′DA′,
∴∠ADG=∠BDB′=2x,
∴∠DGA′=180°-2x-y,
∵∠BEB′=∠EBD+∠EB′D+∠BDB′,
∴∠BEB′=180°-y+2x,
∵EC=EB′,
1 1
∴∠EB′C=∠ECB′= ∠BEB′=90°- y-x,
2 2
1 1
∴∠GB′C=∠A′B′E-∠EB′C=180-y-(90°- y-x)=90°- y+x
2 2
∴∠CGA′=2∠GB′C,
∵∠CGA′=∠GB′C+∠GCB′,
∴∠GB′C=∠GCB′,
∴GC==GB′,
∵EB′=EC,
∴EG⊥CB′,
∵DE∥CB′,
27 |∴DE⊥EG,
∴∠DEG=90°;
【综合运用】结论:DG2=EG2+ 49 B′C2.
16
理由:如图(3)中,延长 DG 交 EB′的延长线于点 T,过点 D 作 DR⊥GA′
交GA′的延长线于点 R.
设 GC=GB′=x,CD=A′D=A′B′=2a,
∵∠B=60°,
∴∠A=∠DA′B′=120°,
∴∠DA′R=60°,
∴A′R=A′D•cos60°=a,DR=√3a
在 Rt△DGR中,则有(2a+x)2=(√3a)2 +(3a−x)2,
5
∴x= a,
4
4 6
∴GB′= a,A′G= a,
5 5
∵TB′∥DA′,
TB′ GB′
∴ = ,
DA′ GA′
4
TB′ a
∴ =5
2a 6 a
5
4
∴TB′= a
3
∵CB′∥DE,
4
CB′ TB′ a 4
∴ = = 3 =
DE ET a+ 4 a 7
3
7
∴DE= CB′,
4
28 |∵∠DEG=90°,
∴DG2=EG2+DE2,
∴DG2=EG2+ 49 B′C2.
16
29 |