文档内容
永州市 2022 年初中学业水平考试数学试卷
温馨提示:1、本试卷包括试题卷和答题卡.考生作答时,选择题和非选择题均须作答在答题卡
上,在本试卷上作答无效.考生在答题卡上按答题卡中注意事项的要求答题.
2、考试结束后,将本试卷和答题卡一并交回.
3、本试题卷共6页,如有缺页.请申明.
4、本试题卷共三道大题,26个小题.满分150分,考试时量120分钟.
一、选择题(本大题共10个小题,每小题4分,共40分.每个小题只有一个正确选项,请将正
确的选项填涂到答题卡上)
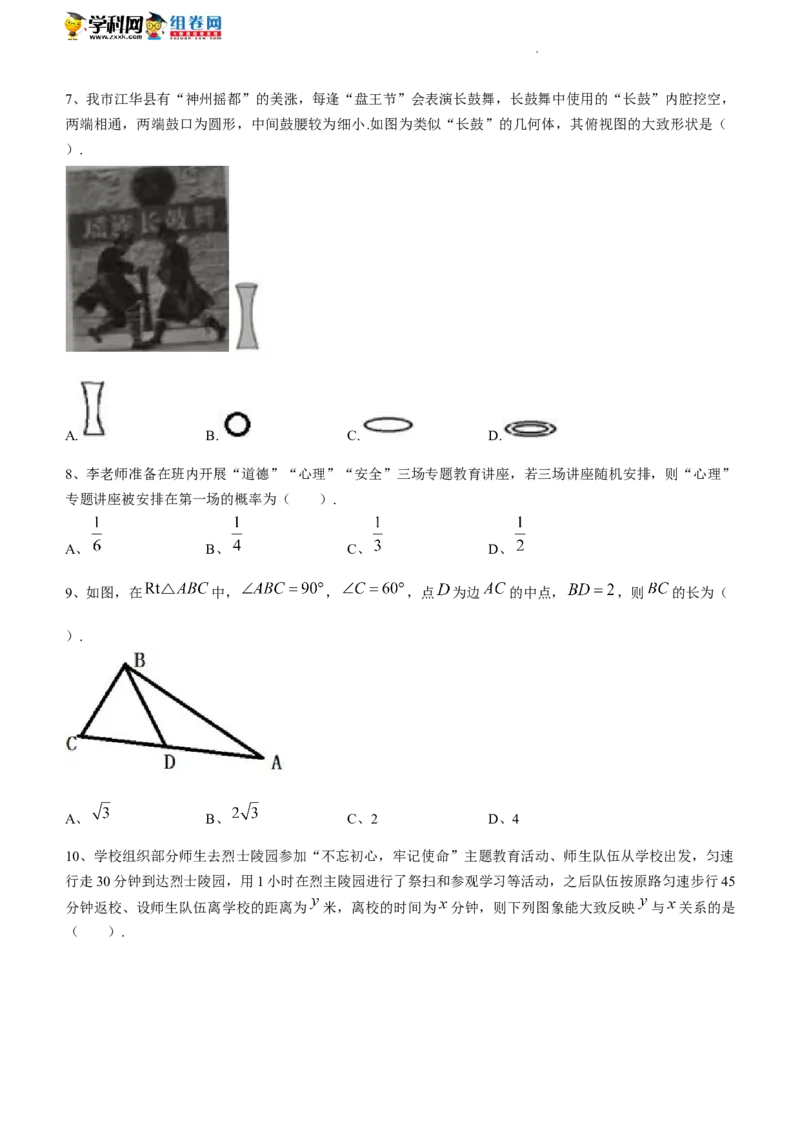
1、如图,数轴上点 对应的实数是( ).
A. B. C.1 D.2
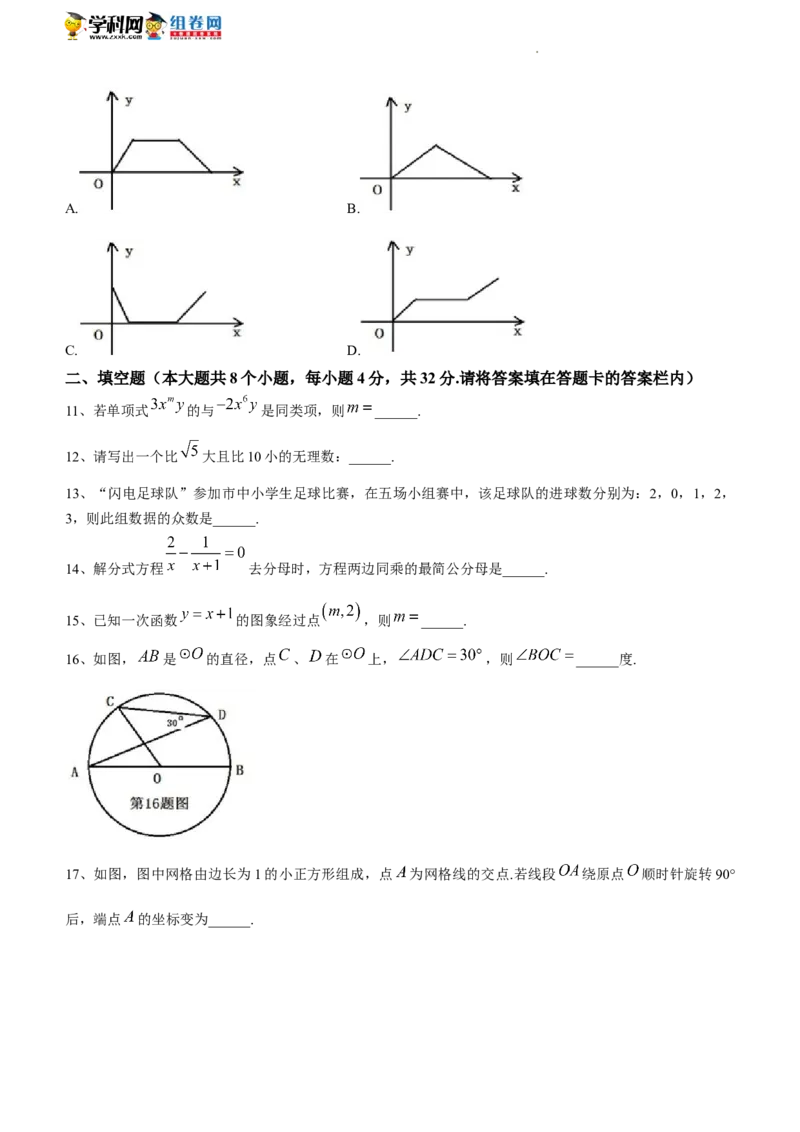
2、下列多边形具有稳定性的是( )
A. B. C. D.
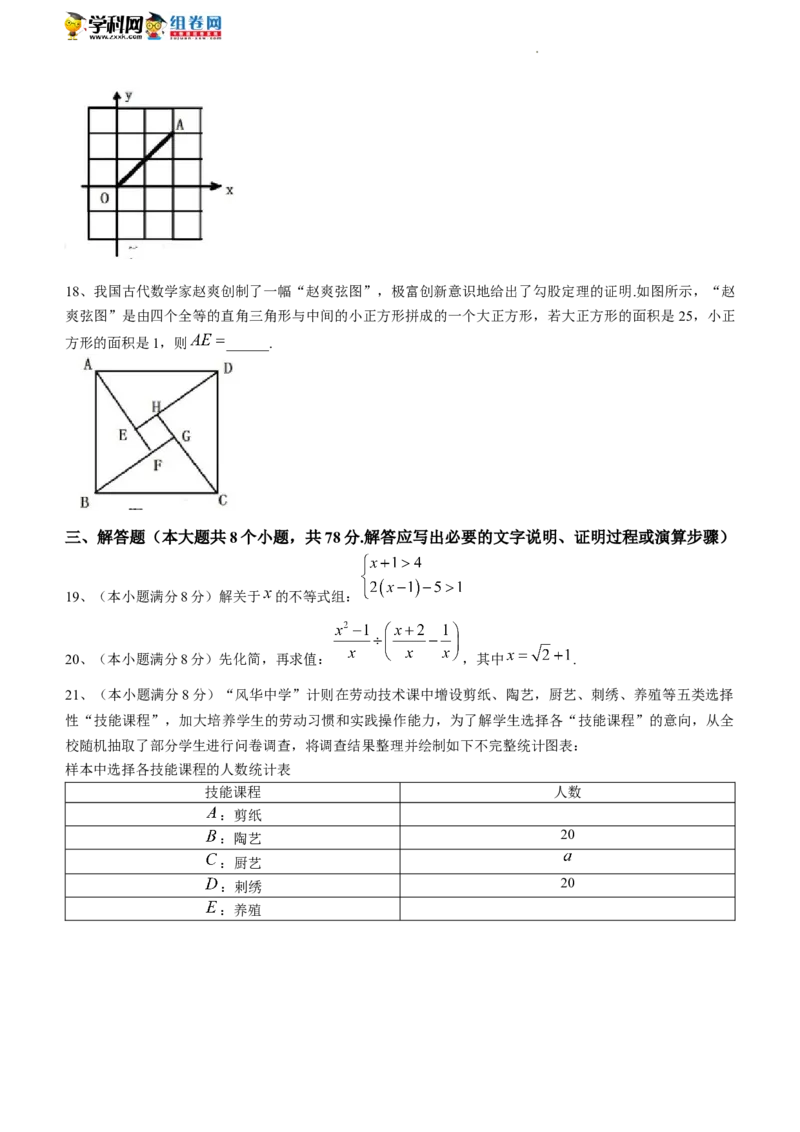
3、剪纸是我国具有独特艺术风格的民间艺术,反映了劳动人民对现实生活的深刻感悟.下列剪纸图形中,是
中心对称图形的有( )
① ② ③ ④
A、①②③ B、①②④ C、①③④ D、②③④
4、水州市大力发展“绿色养殖”,单生猪养殖2021年共出栏7791000头,同比增长29.33%,成为湖南省生
猪产业发展高地和标杆、将数7791000用科学记数法表示为( ).
A、 B、 C、 D、
5、下列各式正确的是( ).
A、 B、 C、 D、
6、下列因式分解正确的是( )
A、 B、
C、 D、
学科网(北京)股份有限公司7、我市江华县有“神州摇都”的美涨,每逢“盘王节”会表演长鼓舞,长鼓舞中使用的“长鼓”内腔挖空,
两端相通,两端鼓口为圆形,中间鼓腰较为细小.如图为类似“长鼓”的几何体,其俯视图的大致形状是(
).
A. B. C. D.
8、李老师准备在班内开展“道德”“心理”“安全”三场专题教育讲座,若三场讲座随机安排,则“心理”
专题讲座被安排在第一场的概率为( ).
A、 B、 C、 D、
9、如图,在 中, , ,点 为边 的中点, ,则 的长为(
).
A、 B、 C、2 D、4
10、学校组织部分师生去烈士陵园参加“不忘初心,牢记使命”主题教育活动、师生队伍从学校出发,匀速
行走30分钟到达烈士陵园,用1小时在烈主陵园进行了祭扫和参观学习等活动,之后队伍按原路匀速步行45
分钟返校、设师生队伍离学校的距离为 米,离校的时间为 分钟,则下列图象能大致反映 与 关系的是
( ).
学科网(北京)股份有限公司A. B.
C. D.
二、填空题(本大题共8个小题,每小题4分,共32分.请将答案填在答题卡的答案栏内)
11、若单项式 的与 是同类项,则 ______.
12、请写出一个比 大且比10小的无理数:______.
13、“闪电足球队”参加市中小学生足球比赛,在五场小组赛中,该足球队的进球数分别为:2,0,1,2,
3,则此组数据的众数是______.
14、解分式方程 去分母时,方程两边同乘的最简公分母是______.
15、已知一次函数 的图象经过点 ,则 ______.
16、如图, 是 的直径,点 、 在 上, ,则 ______度.
17、如图,图中网格由边长为1的小正方形组成,点 为网格线的交点.若线段 绕原点 顺时针旋转90°
后,端点 的坐标变为______.
学科网(北京)股份有限公司18、我国古代数学家赵爽创制了一幅“赵爽弦图”,极富创新意识地给出了勾股定理的证明.如图所示,“赵
爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,若大正方形的面积是 25,小正
方形的面积是1,则 ______.
三、解答题(本大题共8个小题,共78分.解答应写出必要的文字说明、证明过程或演算步骤)
19、(本小题满分8分)解关于 的不等式组:
20、(本小题满分8分)先化简,再求值: ,其中 .
21、(本小题满分8分)“风华中学”计则在劳动技术课中增设剪纸、陶艺,厨艺、刺绣、养殖等五类选择
性“技能课程”,加大培养学生的劳动习惯和实践操作能力,为了解学生选择各“技能课程”的意向,从全
校随机抽取了部分学生进行问卷调查,将调查结果整理并绘制如下不完整统计图表:
样本中选择各技能课程的人数统计表
技能课程 人数
:剪纸
:陶艺 20
:厨艺
:剌绣 20
:养殖
学科网(北京)股份有限公司请根据上述统计数据解决下列问题:
(1)扇形统计图中 ______
(2)厅抽取样本的样本容量是______.频数统计表中 ______.
(3)若该校有2000名学生,请你估计全校有意向选择“养殖”技能课程的人数.
22、(本小题满分10分)受第24届北京冬季奥林匹克运动会的形响,小勇爱上了雪上运动.一天,小勇在滑
雪场训练滑雪,第一次他从滑雪道 端以平均 米/秒的速度滑到 端,用了24秒;第二次从滑雪道
端以平均 米/秒的速度滑到 端,用了20秒.
(1)求 的值;
(2)设小勇从滑雪道 端滑到 瑞的平均速度为 米/秒,所用时间为 秒,请用含 的代数式表示 (不要
求写出 的取值范围).
23、(本小题满分10分)如图, 是平行四边形 的对角线, 平分 ,交 于点 .
(1)请用尺规作 的角平分线 ,交 于点 (要求保留作图痕迹,不写作法,在确认答案后,
请用黑色笔将作图痕迹再填涂一次):
(2)根据图形猜想四边形 为平行四边形,请将下面的证明过程补充完整.
证明:∵四边形 是平行四边形,
∴
∵ ______.(两线平行,内错角相等).
又∵ 平分 , 平分 ,
学科网(北京)股份有限公司∴ ,
∴ .
∴ ______(______)(填推理的依据)
又∵四边形 是平行四边形.
∴ .
∴四边形 为平行四边形(______)(填推理的依据),
24、(本小题满分10分)为提高耕地灌溉效率,小明的爸妈准备在耕地 、 、 、 四个位置安装四个
自动喷酒装置(如图1所示), 、 、 、 四点恰好在边长为50米的正方形的四个顶点上,为了用水
管将四个自动喷洒装置相互连通,爸妈设计了如下两个水管铺设方案(各图中实线为铺设的水管).
方案一:如图2所示,沿正方形 的三边铺设水管;
方案二:如图3所示,沿正方形 的两条对角线铺设水管.
(1)请通过计算说明上述两方案中哪个方案铺设水管的总长度更短:
(2)小明看了爸妈的方案后,根据“蜂集原理”重新设计了一个方案(如图4所示),
满足 , , 、请将小明的方案与爸妈的方案比较,
判断谁的方案中铺设水管的总长度更短,并说明理由.(参考数据: , )
25、(本小题满分12分)如图,已知 , 是 的直径, 是 的切线,点 在 的延长线
上, , 交于点 ,
(1)求证: ;
(2)求证: ;
(3)若 的面积 ,求四边形 的面积 .
学科网(北京)股份有限公司26、(本小题满分12分)已知关于 的函数 .
(1)若 ,函数的图象经过点 和点 ,求该函数的表达式和最小值;
(2)若 , , 时,函数的图象与 轴有交点,求 的取值范围.
(3)阅读下面材料:
设 ,函数图象与 轴有两个不同的交点 , ,若 , 两点均在原点左侧,探究系数 , , 应
满足的条件,根据函数图像,思考以下三个方面:
①因为函数的图象与 轴有两个不同的交点,所以 ;
②因为 , 两点在原点左侧,所以 对应图象上的点在 轴上方,即 ;
③上述两个条件还不能确保 , 两点均在原点左侧,我们可以通过抛物线的对称轴位置来进一步限制抛物
线的位置:即需 .
综上所述,系数 , , 应满足的条件可归纳为:
请根据上面阅读材料,类比解决下面问题:
若函数 的图象在直线 的右侧与 轴有且只有一个交点,求 的取值范围.
永州市 2022 年初中学业水平考试数学试卷
参考答案
一、选择题(本大题共10个小题,每小题4分,共40分.每个小题只有一个正确选项,请将正
学科网(北京)股份有限公司确的选项填涂到答题卡上)
1-5 ADACD 6-10 BBCCA
二、填空题(本大题共8个小题,每小题4分,共32分.请将答案填在答题卡的答案栏内)
11、6 12、 (答案不唯一) 13、2 14、
15、1 16、120 17、 18、3
三、解答题(本大题共8个小题,共78分.解答应写出必要的文字说明、证明过程或演算步骤)
19、解:解不等式(1)得 ,
解不等式(2),得
所以,原不等式组的解集是
20、解:原式
当 时,原式
21、(1)20 (2)200 50
(3)解: (人)
答:全校有意向选择“养殖”技能课程的学生约200人.
22、解:(1)根据题意,得 解这个方程,得
(2)
23、证明:∵四边形 是平行四边形,
∴
∵ .(两线平行,内错角相等).
又∵ 平分 , 平分 ,
∴ ,
∴ .
∴ (内错角相等,两线平行)(填推理的依据)
又∵四边形 是平行四边形.
学科网(北京)股份有限公司∴ .
∴四边形 为平行四边形(两组对边分别平行的四边形是平行四边形)(填推理的依据)
24、解:(1)方案一: (米)
方案二: (米)
所以方案二总长度更短.
(2)如图,作 , ,垂足分别为 和 .则容易证明(省略)
∵ ,
∴ (米),
,
总长度: (米)
∵
所以小明的方案总长度最短.
25、证明:(1)∵ 是 的直径, 是 的切线,
∴ ,
∴
∴
(2)∵ ,∴
∵ ,
∴
∵ 是直径,∴
∵ ,∴
∴
(3)∵ ∴
学科网(北京)股份有限公司∴
∴
∵
∴ , ,
∴
26、解:(1)根据题意,得
解之,得 ,所以
函数的表达式 或 ,当 时, 的最小值是0
( 2 ) 根 据 题 意 , 得 而 函 数 的 图 象 与 轴 有 交 点 , 所 以
所以
(3)函数 的图象
图1: 即
所以, 的值不存在.
学科网(北京)股份有限公司图2: 即 的值 .
图3: 即
所以 的值不存在
图4: 即
所以 的值不存在.
图5:
即
所以 的值为
图6: 函数与 轴的交点为
所以 的值为0成立.
综上所述, 的取值范围是 或 .
学科网(北京)股份有限公司学科网(北京)股份有限公司