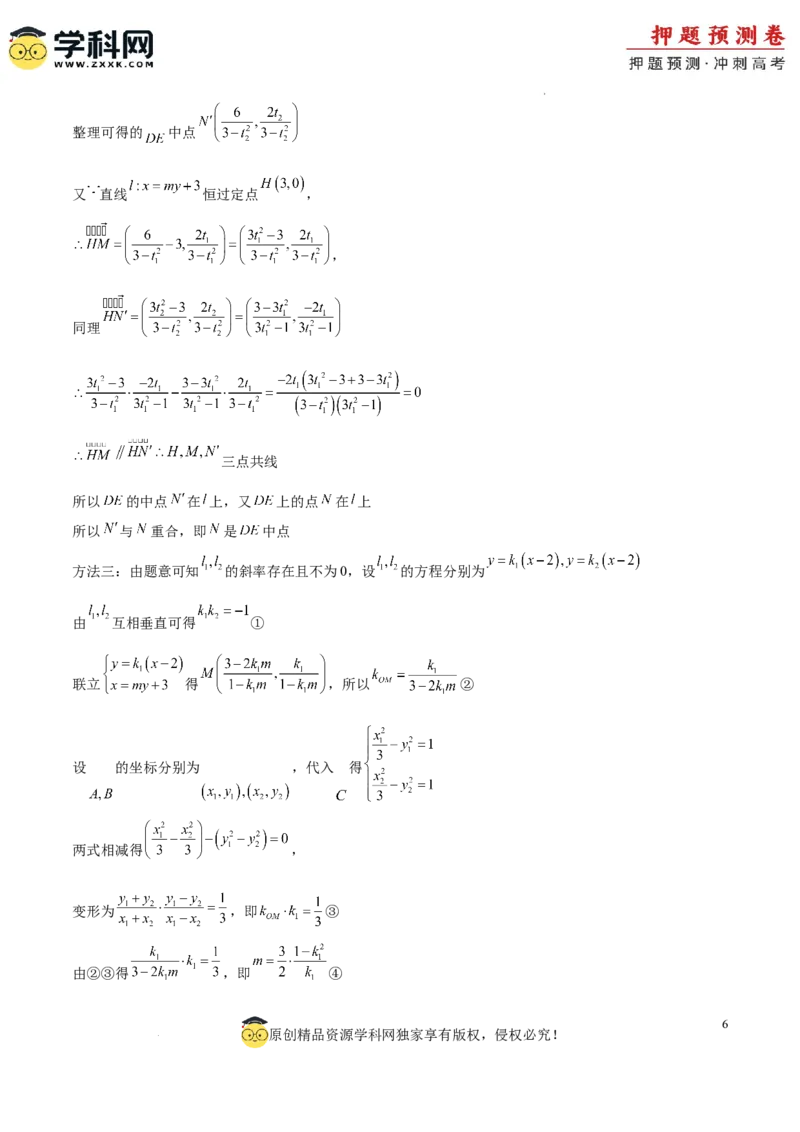文档内容
2024年高考押题预测卷03【全国卷】
数学(文科)·参考答案
第一部分(选择题 共60分)
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合要求
的。
1 2 3 4 5 6 7 8 9 10 11 12
B B C A A C D B B B C B
第二部分(非选择题 共90分)
二、填空题:本题共4小题,每小题5分,共20分。
13. 14. / 15. 16.
三、解答题:共70分,解答应写出必要的文字说明、证明过程及验算步骤.第17~21题为必考题,每个试
题考生都必须作答,第22、23题为选做题,考生根据要求作答。
(一)必考题:共60分.
17.(12分)
【详解】(1)平均数 ,
由 , ,
故中位数位于 ,设中位数为 ,则有 ,解得 ,
即平均数 ,中位数 ;
(2) ,
故有99.5%的把握认为能否获得“亚运达人”称号与性别有关.
18.(12分)
【详解】(1)因为 成等比数列,且 ,
所以 ,由 ,解得 ,
所以 .
1
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司(2)由 ,
得 ,
由 ,有 ,所以 ,得 .
19.(12分)
【详解】(1)在等腰梯形 中,因为 ,
所以 , ,
所以 ,所以 .
因为平面 平面 ,平面 平面 平面 ,
所以 平面 .
又 平面 ,所以 .
又 平面 ,所以 平面 .
又 平面 ,所以平面 平面 .
(2)如图,过点 作 于点 ,由(1)可知平面 平面 ,
又平面 平面 平面 ,所以 平面 ,故 .
在 中, ,所以 .
在 中, ,所以 .
又 ,所以 ,即四棱锥 的高为1.
2
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司由题意知,梯形 的高为 ,所以梯形 的面积为 ,
所以四棱锥 的体积为 .
20.(12分)
【详解】(1)由 可得 ,
则 ,所以曲线 在点 处的切线斜率为 ,
又因为 ,所以切线方程为: ,即 .
所以 .
(2)要证明 ,只要证 ,
设 ,则 ,
令 ,则 ,
所以 在 上单调递减,又 ,
所以当 时, ,则 在 上单调递增,
当 时, ,则 在 上单调递减,
所以 ,所以 .
21.(12分)
【详解】(1)由题意知 ,
所以 的方程为
3
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司直线 的倾斜角为 ,过点 直线 的方程为
设 ,联立 ,
得
与 互相垂直 的倾斜角为 由对称性可知
(2)方法一:由题意可知 的斜率存在且不为0,设 的方程分别为 由
互相垂直可得 ①
联立 得 ②
联立 ,
整理得
是 的中点 ③
4
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司由②③得 ,即 ④
同理联立 得 ⑤
由①④⑤得
⑥
联立 ,
得
取 中点 ,所以 ⑦
由⑥⑦得 与 重合,即 是 中点.
方法二:由题意可知 的斜率存在且不为0,设 的方程分别为
由 互相垂直可得
设 的坐标分别为
联立 ,
得 ,又
是 的中点
5
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司整理可得的 中点
又 直线 恒过定点 ,
,
同理
三点共线
所以 的中点 在 上,又 上的点 在 上
所以 与 重合,即 是 中点
方法三:由题意可知 的斜率存在且不为0,设 的方程分别为
由 互相垂直可得 ①
联立 得 ,所以 ②
设 的坐标分别为 ,代入 得
两式相减得 ,
变形为 ,即 ③
由②③得 ,即 ④
6
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司同理联立 得 ,
所以 ⑤
由①④⑤得 ,
所以 ⑥
取 中点 ,同理可证 ⑦
由⑥⑦得 .
结合 均在直线 上,所以 与 重合,即 是 中点.
(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做。则按所做的第一题记分.
22.(10分)
【详解】(1)由题设曲线 的参数方程,消参得 ,
由 ,且 得, ,化简得
,
C的普通方程为 ,l直角坐标方程为 .
(2)当 时, ,易知 ,设 ,
7
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司可得 , (a
是参数),
消参得方程为 且 ,
则圆心距离 得 ,
则两圆相交,故两圆存在公共点,联立方程组 ,
解得 或 ,故坐标为 .
23.(10分)
【详解】(1)不存在 , , ,使得 .理由如下:
因为 , , 都是正数,且 ,所以 ,
所以
,
当且仅当 ,即 时取等号,
即 的最小值为 ,
所以不存在 , , ,使得 .
(2)因为
8
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司,当且仅当 时等号成立,
所以 .
9
原创精品资源学科网独家享有版权,侵权必究!
学科网(北京)股份有限公司