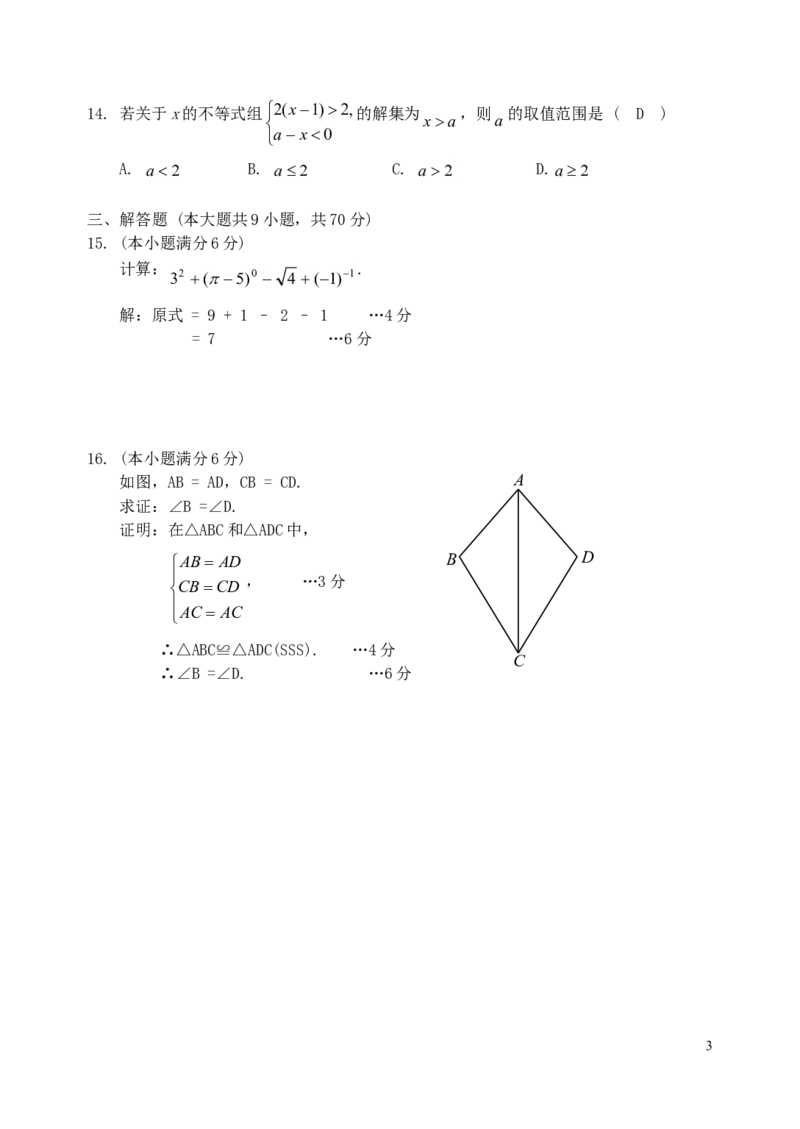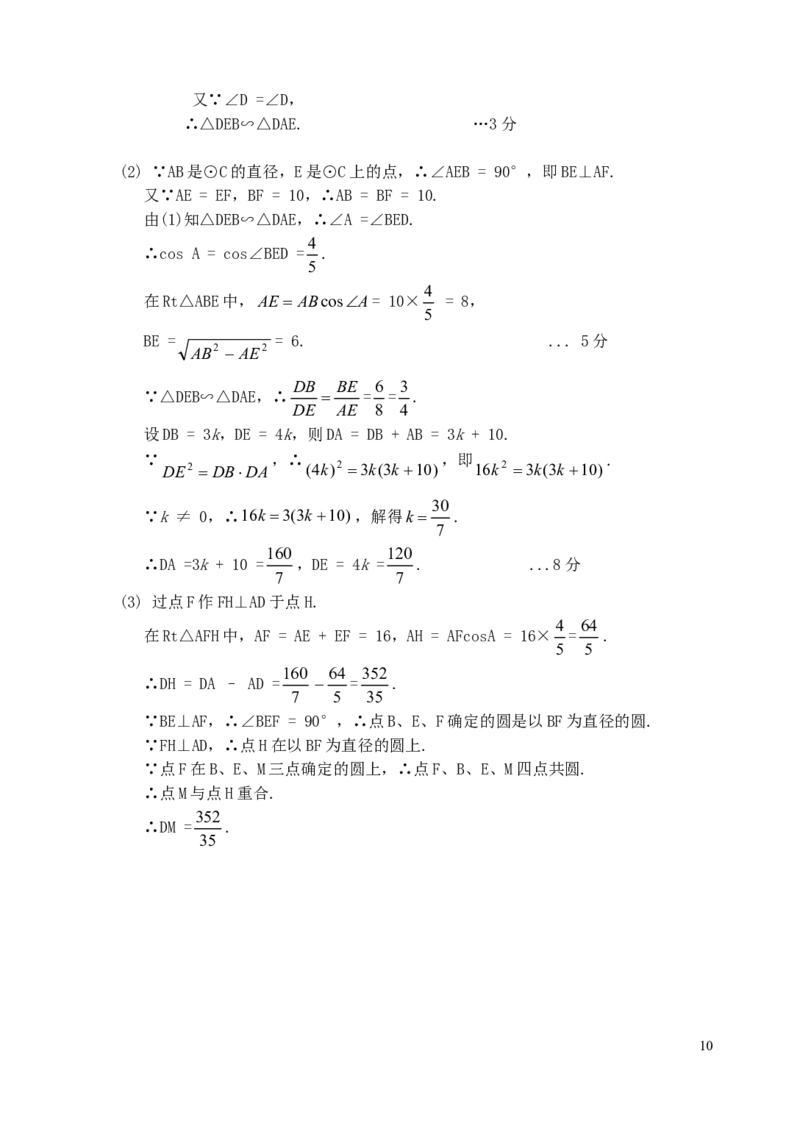云南省昆明市2019年中考数学真题试题_中考真题_2.数学中考真题2015-2024年_2019年全国中考数学206份

云南省2019年中考数学试卷 (全卷三个大题，共23题，共8页；满分120分，考试用时120分钟) 注意事项： 1. 本卷为试题卷，考生必须在答题卡上解题作答. 答案应写在答题卡的相应位置上，在 试题卷、草稿纸上作答无效. 2. 考试结束后，请将试卷和答题卡一并交回. 一、填空题 (本大题共6小题，每小题3分，共18分) 1. 若零上8°C记作 +8°C，则零下6°C记作 -6 °C. 2. 分解因式： = (x – 1 ) 2 . x2 2x1 1 A B 3. 如图，若AB∥CD，∠1= 40°， 2 C D 则∠2 = 140 度. k 4. 若点(3，5)在反比例函数y (k 0)的图象上，则k = 15 . x 5. 某中学九年级甲、乙两个班参加了一次数学考试，考试人数每班都为40人，每个班的 考试成绩分为A、B、C、D、E五个等级，绘制的统计图如下： 甲班数学成绩频数分布直方图 乙班数学成绩扇形统计图 人数 13 12 C B 35% 10% 8 A 5% 5 D E 20% 30% 2 O A B C D E 等级 根据以上统计图提供的信息，则D等级这一组人数较多的班是 甲班 . 6. 在平行四边形ABCD中，∠A= 30°，AD = ，BD = 4，则平行四边形ABCD的面 4 3 积等于 或 8 . 16 3 3 1D C D C A E B A E B 二、选择题 (本大题共8小题，每小题4分，共32分，每小题正确的选项只有一个) 7. 下列图形既是轴对称图形，又是中心对称图形的是 ( B ) A. B. C. D. 8. 2019年“五一“期间，某景点接待海内外游客共688000人次，688000这个数用科学 记数法表示为 ( C ) A. B. C. D. 68.8104 0.688106 6.88105 6.88106 9. 一个十二边形的内角和等于 ( D ) A. 2160° B. 2080° C. 1980° D. 1800° x1 10. 要使 有意义，则x的取值范围为 ( B ) 2 A. x0 B. x1 C. x0 D.x1 11. 一个圆锥的侧面展开图是半径为8的半圆，则该圆锥的全面积是 ( A ) A. 48π B. 45π C. 36π D. 32π 12. 按一定规律排列的单项式： ， ， ， ， ，……，第n个单项式是( C ) x3 x5 x7 x9 x11 A. B. (1)n1x2n1 (1)nx2n1 C. D. (1)n1x2n1 (1)nx2n1 13. 如图，△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F，且AB = 5，BC = 13，CA = 12，则阴影部分(即四边形AEOF)的面积是 ( A ) A E A. 4 B. 6.25 F C. 7.5 O D.9 B D C 214. 若关于x的不等式组2(x1)2,的解集为 ，则 的取值范围是 ( D )  xa a ax0 A. a2 B. a2 C. a2 D.a2 三、解答题 (本大题共9小题，共70分) 15. (本小题满分6分) 计算： . 32 (5)0  4 (1)1 解：原式 = 9 + 1 – 2 – 1 …4分 = 7 …6分 16. (本小题满分6分) 如图，AB = AD，CB = CD. A 求证：∠B =∠D. 证明：在△ABC和△ADC中， AB AD B D  ， …3分 CBCD  AC  AC  ∴△ABC≌△ADC(SSS). …4分 C ∴∠B =∠D. …6分 317. (本小题满分8分) 某公司销售部有营业员15人，该公司为了调动营业员的积极性，决定实行目标管 理，根据目标完成的情况对营业员进行适当的奖励，为了确定一个适当的月销售目标， 公司有关部门统计了这15人某月的销售量，如下表所示： 月销售量/件数 1770 480 220 180 120 90 人数 1 1 3 3 3 4 (1) 直接写出这15名营业员该月销售量数据的平均数、中位数、众数； (2) 如果想让一半左右的营业员都能达到月销售目标，你认为(1)中的平均数、中 位数、众数中，哪个最适合作为月销售目标？请说明理由. 温馨提示：确定一个适当的月销 售目标是一个关键问题，如果目标定 得太高，多数营业员完不成任务，会 使营业员失去信心；如果目标定得太 低，不能发挥营业员的潜力. 解：(1) 这15名营业员该月销售量数据的平均数、中位数、众数分别是 278，180，90. …6分 (2) 中位数最适合作为月销售目标，理由如下： 这15个人中，月销售量不低于278件的只有2人，远低于营业员的一半，月销售量 不低于180件的有8人，占营业员的一半左右，月销售量不低于90件的有15人，即所 有营业员，所以中位数最适合作为月销售目标. …8分 或说：因为从统计的数据来看，若目标定为平均数为278，能完成目标的只有2名 员工，根本达不到一半左右的营业员都能达到月销售目标；若目标定为众数94，所有 营业员都能达到月销售目标；若目标定为平均数180，大概有8人能达到月销售目标， 占营业员的一半左右，所以中位数最适合作为月销售目标. 418. (本小题满分6分) 为进一步营造扫黑除恶专项斗争的浓厚宣传氛围，推进平安校园建设，甲、乙两所 学校各租用一辆大巴车组织部分师生，分别从距目的地240千米和270千米的两地同 时出发，前往“研学教育“基地开展扫黑除恶教育活动，已知乙校师生所乘大巴车的 平均速度是甲校师生所乘大巴车的平均速度的1.5倍，甲校师生比乙校师生晚1小时 到达目的地，分别求甲、乙两所学校所乘大巴车的平均速度. 解：设甲学校所乘大巴车的平均速度为x千米/小时， 则乙学校所乘大巴车的平均速度为1.5x千米/小时， 240 270 依题意，得  1. …3分 x 1.5x 解得 x60. 经检验x60是所列方程的解. ∴x60，1.5x = 90. 答：甲、乙两所学校所乘大巴车的平均速度分别为60千米/小时和90千米/小时. …6分 19. (本小题满分7分) 甲、乙两同学玩一个游戏：在一个不透明的口袋中装有标号分别为1，2，3，4的四 个小球(除标号外无其它差异). 从口袋中随机摸出一个小球，记下标号后放回口袋中， 充分摇匀后，再从口袋中随机摸出一个小球，记下该小球的标号，两次记下的标号分别 用x、y表示，若x y为奇数，则甲获胜；若x y为偶数，则乙获胜. (1) 用列表法或树状图法(树状图也称树形图)中的一种方法，求(x，y)所有可能 出现的结果总数； (2) 你认为这个游戏对双方公平吗？请说明理由. 解：(1) 所有可能的结果如下表： y 1 2 3 4 x 1 (1，1) (1，2) (1，3) (1，4) 2 (2，1) (2，2) (2，3) (2，4) 3 (3，1) (3，2) (3，3) (3，4) 4 (4，1) (4，2) (4，3) (4，4) ∴(x，y)所有可能出现的结果总数为16种. …4分 5(2) 这个游戏对双方是公平的，理由如下： 共有16种等可能的结果，x y分别是2，3，4，5；3，4，5，6；4，5，6，7；5，6，7，8， x y为奇数的结果有8种；x y为偶数的结果有8种， ∴这个游戏对双方是公平的.(个人认为到此就可说明是公平的，但出题人不这样认为. 8 1 8 1 ∴P (甲获胜) =  ，P (乙获胜) =  ，∴P (甲获胜)= P (乙获胜). 16 2 16 2 ∴这个游戏对双方是公平的. …7分 20. (本小题满分8分) 如图，四边形ABCD中，对角线AC、BD相交于点O，AO = OC，BO = OD，且∠AOB = 2∠OAD. (1) 求证：四边形ABCD是矩形； (2) 若∠AOB：∠ODC = 4：3，求∠ADO的度数. A D (1) 证明：∵AO = OC，BO = OD， ∴四边形ABCD是平行四边形. …1分 O ∵∠AOB = 2∠OAD，∠AOB = ∠OAD+∠ODA， B C ∴∠OAD =∠ODA. …2分 ∴AO = DO. …3分 ∴AO = OC = BO = OD， ∴AC = BD. ∴四边形ABCD是矩形. …4分 (2) 设∠AOB = 4x°，∠ODC = 3x°，则∠COD = 4x°，∠OCD = 3x°. …5分 在△COD中，∠COD +∠OCD +∠ODC = 180°， …6分 ∴4x + 3x + 3x = 180， 解得x = 18，∴∠ODC = 3x° = 54°， …7分 ∴∠ADO = 90° - ∠ODC = 90° – 54° = 36°. …8分 621. (本小题满分8分) 已知k是常数，抛物线 的对称轴是y轴，并且与x轴有 yx2 (k2 k 6)x3k 两个交点. (1) 求k的值； (2) 若点P在抛物线 上，且P到y轴的距离是2，求点 yx2 (k2 k 6)x3k P的坐标. 解：(1) ∵抛物线 的对称轴是y轴。 yx2 (k2 k 6)x3k k2 k 3 ∴ 0，∴k2 k 60，解得k = -3或2. …2分 2 当k = -3时，抛物线为 ，与x轴有两个交点，符合题意； yx2 9 当k = 2时，抛物线为 ，与x轴没有交点，不符合题意，舍去. yx2 6 ∴k = -3. …4分 (2) 由(1)可知，抛物线为 . yx2 9 7∵P到y轴的距离是2，∴点P的横坐标为2或 – 2. ∴当x = 2或– 2时，y = – 5， …6分 ∴点P的坐标为(2，–5)或(–2，–5). …8分 22. (本小题满分9分) 某驻村扶贫小组实施产业扶贫，帮助贫困户进行西瓜种植和销售. 已知西瓜的成 本为6元/千克，规定销售单价不低于成本，又不高于成本的两倍. 经过市场调查发现， 某天西瓜的销售量y (千克)与销售单价x (元/千克)的函数关系如下图所示： (1) 求y与x的函数解析式(也称关系式)； (2) 求这一天销售西瓜获得的利润W的最大值. y 1000 200 O 6 8 10 12 x 解：(1) 当6 ≤ x ≤12时，由图可知，y是x的一次函数，设y = kx + b， 把(6，1000)，(10，200)分别代入，得 86k b1000，解得k 200，∴ . …2分   y200x2200 10k b200 b2200 当10 < x ≤ 12时， y = 200. ∴y与x的函数解析式为 200x2200 (6x10) . …4分 y 200 (10x12) (2) 若6 ≤ x ≤12， = . W (x6)(200x2200) 200(x8.5)2 1250 ∴当x = 8.5时，W = 1250 (元). …6分 max 若10 < x ≤ 12，W (x6)200=200x1200 ∵200 > 0，∴W随x的增大而增大， ∴x = 12，W = 1200 (元). …8分 max ∵1250 > 1200， ∴这一天销售西瓜获得的利润W的最大值为1250元. 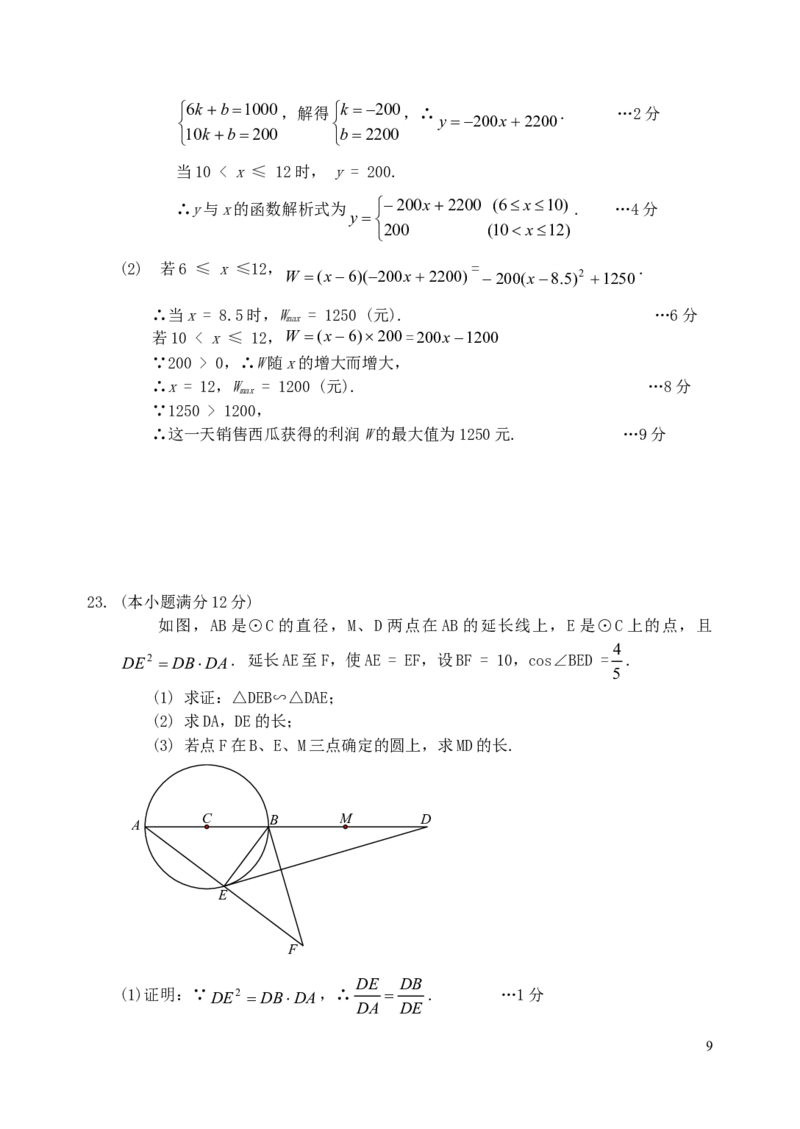…9分 23. (本小题满分12分) 如图，AB是⊙C的直径，M、D两点在AB的延长线上，E是⊙C上的点，且 4 DE2 DBDA. 延长AE至F，使AE = EF，设BF = 10，cos∠BED = . 5 (1) 求证：△DEB∽△DAE； (2) 求DA，DE的长； (3) 若点F在B、E、M三点确定的圆上，求MD的长. C B M D A E F DE DB (1)证明：∵DE2 DBDA，∴  . …1分 DA DE 9又∵∠D =∠D， ∴△DEB∽△DAE. …3分 (2) ∵AB是⊙C的直径，E是⊙C上的点，∴∠AEB = 90°，即BE⊥AF. 又∵AE = EF，BF = 10，∴AB = BF = 10. 由(1)知△DEB∽△DAE，∴∠A =∠BED. 4 ∴cos A = cos∠BED = . 5 4 在Rt△ABE中，AE  ABcosA= 10× = 8， 5 BE = = 6. ... 5分 AB2  AE2 DB BE 6 3 ∵△DEB∽△DAE，∴  = = . DE AE 8 4 设DB = 3k，DE = 4k，则DA = DB + AB = 3k + 10. ∵ ，∴ ，即 . DE2 DBDA (4k)2 3k(3k 10) 16k2 3k(3k 10) 30 ∵k ≠ 0，∴16k 3(3k 10)，解得k  . 7 160 120 ∴DA =3k + 10 = ，DE = 4k = . ...8分 7 7 (3) 过点F作FH⊥AD于点H. 4 64 在Rt△AFH中，AF = AE + EF = 16，AH = AFcosA = 16× = . 5 5 160 64 352 ∴DH = DA – AD =  = . 7 5 35 ∵BE⊥AF，∴∠BEF = 90°，∴点B、E、F确定的圆是以BF为直径的圆. ∵FH⊥AD，∴点H在以BF为直径的圆上. ∵点F在B、E、M三点确定的圆上，∴点F、B、E、M四点共圆. ∴点M与点H重合. 352 ∴DM = . 35 10C B H M D A E F 1112