文档内容
2024年高考押题预测卷
数学·参考答案
第一部分(选择题 共58分)
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要
求的。
1 2 3 4 5 6 7 8
C A D B C A B D
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部
选对的得6分,部分选对的得部分分,有选错的得0分.
9 10 11
AB AD ACD
第二部分(非选择题 共92分)
三、填空题:本题共3小题,每小题5分,共15分。
12.16 13.8 14.
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步棸。
15.【解析】(1)因为 ,所以 .
(2)样本空间 ,共有36个样本点.
记事件 “数字之和小于7”,事件 “数字之和等于7",事件 “数字之和大于7”.
, ,共15种,
故
,共6种,故 ;
, ,共15种,
1
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司故 ;
从而 的分布列为:
0 1 2
故
16.【解析】(1)由题得, 的定义域为 .
.
的图象在点 处的切线与直线l:2x 垂直,
,解得 .
(2)由(1)知 .
①当 时, 恒成立, 在 上为减函数,此时 无极值;
②当 时,由 ,得 ,由 ,得 ,
在 上单调递减,在 上单调递增,
故 的极小值为 .
综上可得,当 时, 在 上为减函数, 无极值;
当 时, 在 上单调递减,在 上单调递增.
的极小值为 ,无极大值.
2
原创精品资源学科网独家享有版权,侵权必究!
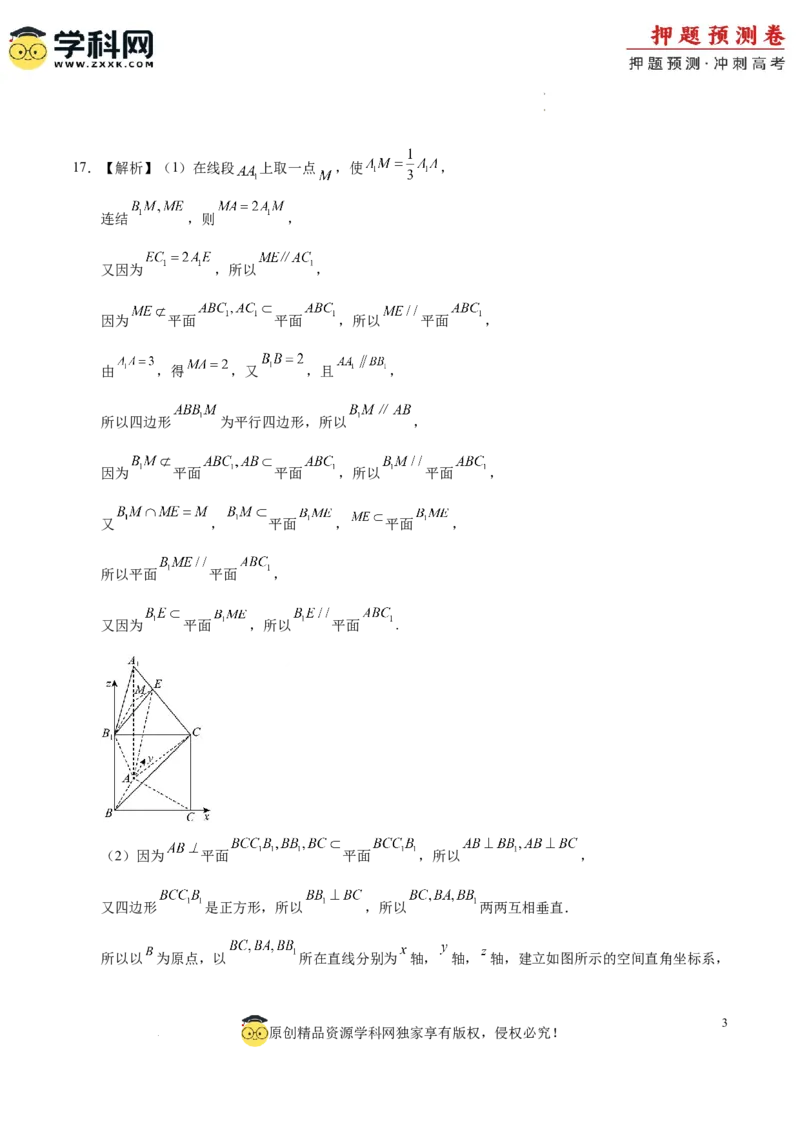
学学科科网网((北北京京))股股份份有有限限公公司司17.【解析】(1)在线段 上取一点 ,使 ,
连结 ,则 ,
又因为 ,所以 ,
因为 平面 平面 ,所以 平面 ,
由 ,得 ,又 ,且 ,
所以四边形 为平行四边形,所以 ,
因为 平面 平面 ,所以 平面 ,
又 , 平面 , 平面 ,
所以平面 平面 ,
又因为 平面 ,所以 平面 .
(2)因为 平面 平面 ,所以 ,
又四边形 是正方形,所以 ,所以 两两互相垂直.
所以以 为原点,以 所在直线分别为 轴, 轴, 轴,建立如图所示的空间直角坐标系,
3
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司由 ,得 ,
于是 , ,
设平面 的法向量为 ,则 ,得 ,即 ,
令 ,得 ,所以平面 的一个法向量 ,
设直线 与平面 所成的角为 ,
则 ,
所以直线 与平面 所成角的正弦值为 .
18.【解析】(1)由题意可得 ,
设 ,则 ,
∵ ,∴ ,化简得: ①,
又 在椭圆上, ②,
由①②得 ,
又 ,∴ ,故椭圆C的标准方程 ;
(2)设直线 的平行线与椭圆相交于点 、 ( 在上方),
直线 的平行线与椭圆相交于点 、 ( 在上方),
∴直线 的方程为 ,直线 的方程为 ,
4
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司又 ,∴ ,
联立 ,解得 ,∴ ,
联立 ,解得 ,∴ ,
设直线EF的倾斜角为 ,直线GH的倾斜角为 , ,
∴ ,
则 ,
,
∴四边形面积为:
,
故该四边形的面积为定值 .
5
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司19.【解析】(1) 中的最小元素为 .
(2)由题得 ,设 , .
①当 时, 或 或
或 或 或 .
经检验,当 时, ,符合题意,所以 .
②当 时, 或 或 或 .
经检验,当 时, ,符合题意,所以 .
③当 时,不符合题意.因此, 或10.
(3)设 ,则 ,其中 ,
,所以 ,
设 ,则 .
因为 ,
所以
.
6
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司因为 ,
所以 ,所以 ,
又因为 ,所以 .
7
原创精品资源学科网独家享有版权,侵权必究!
学学科科网网((北北京京))股股份份有有限限公公司司