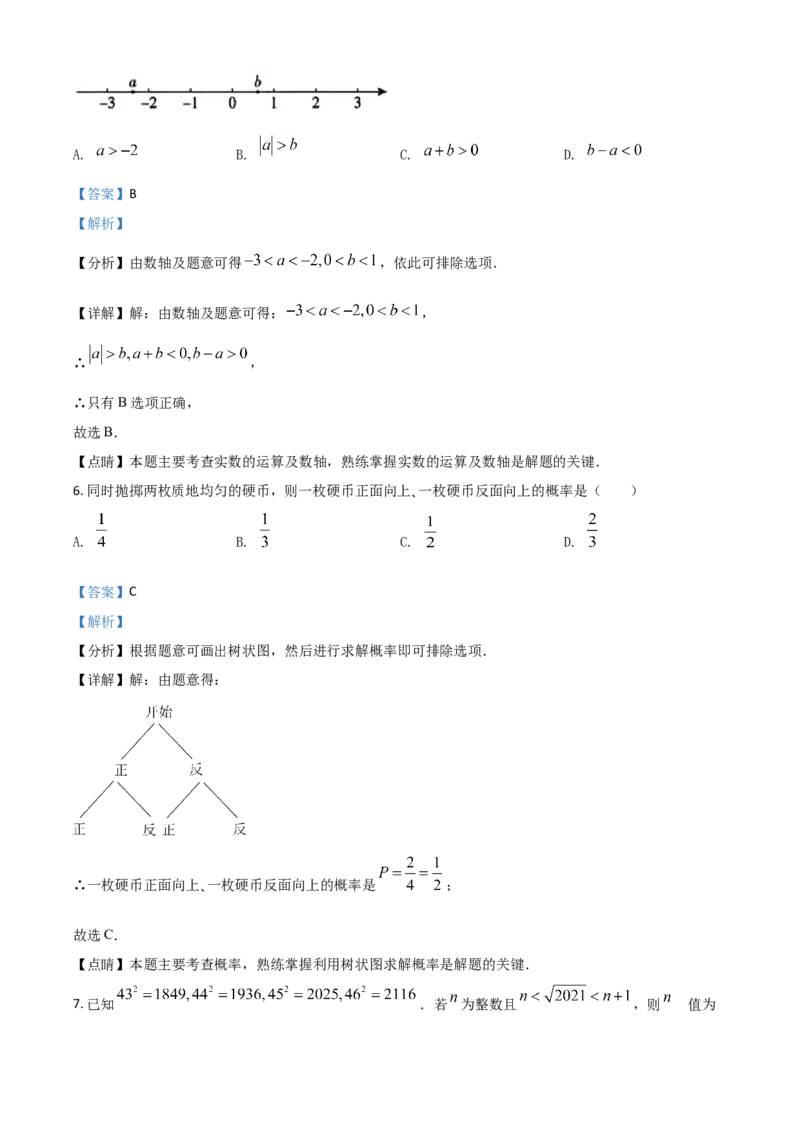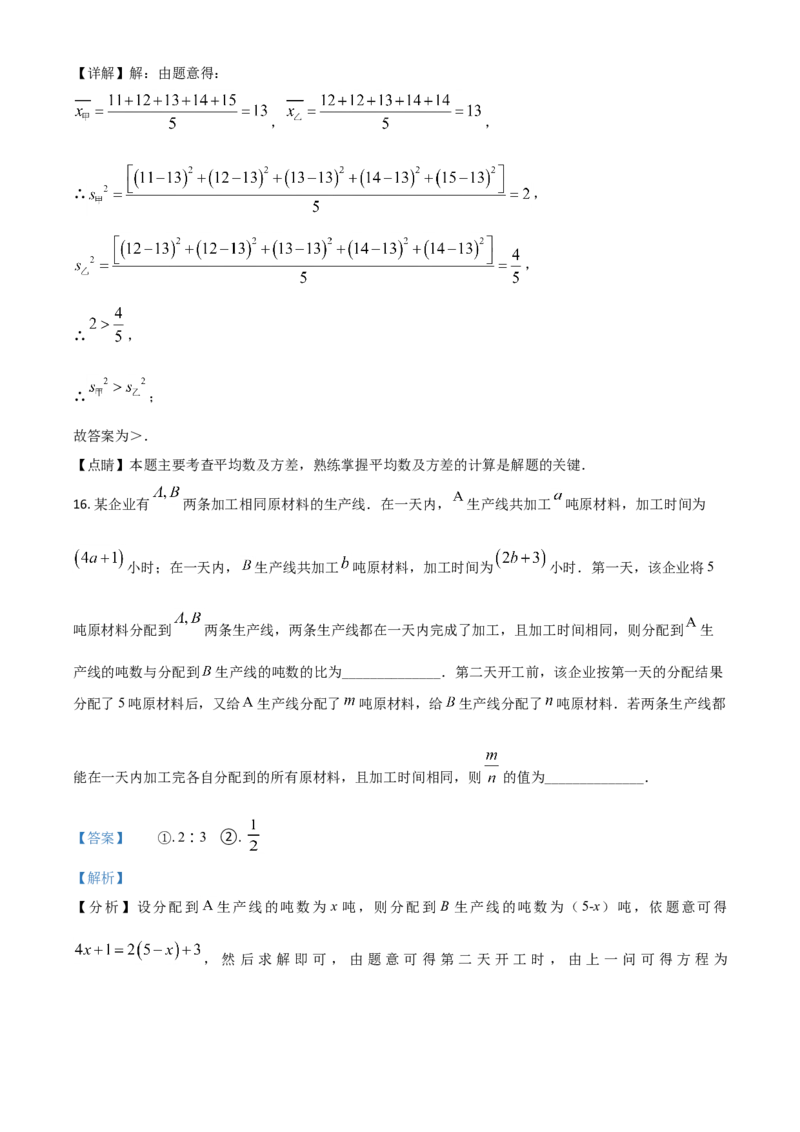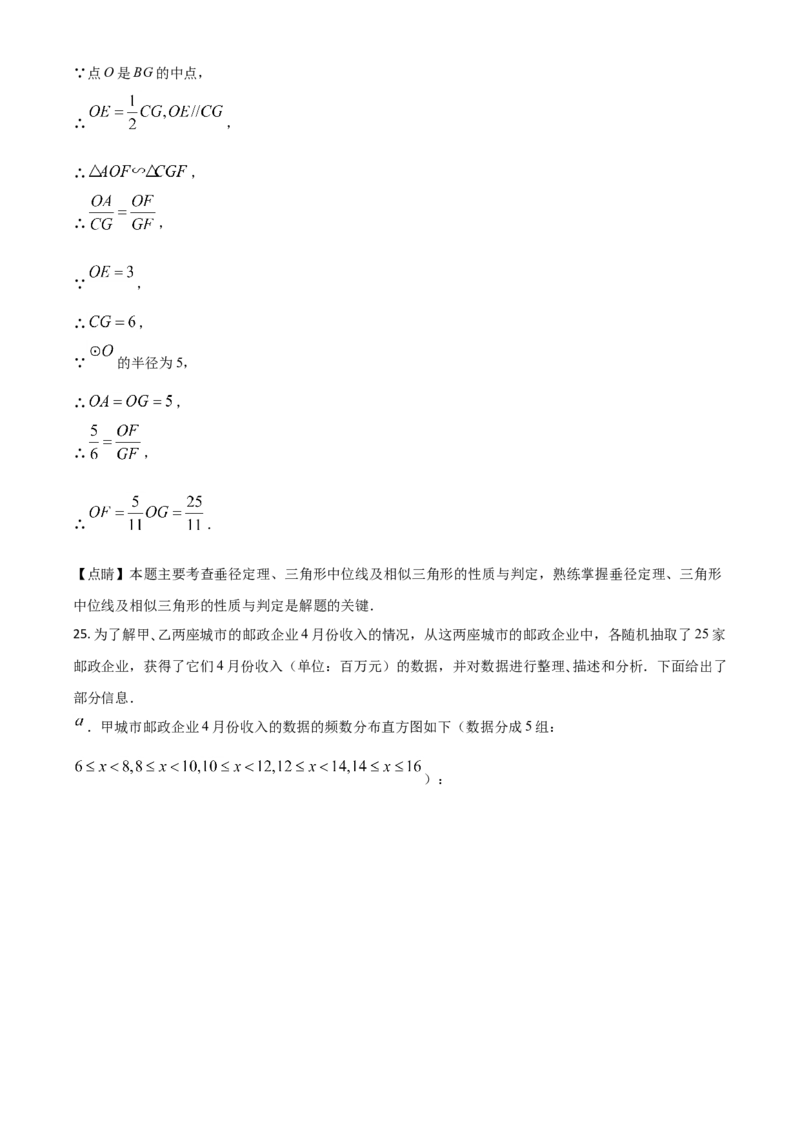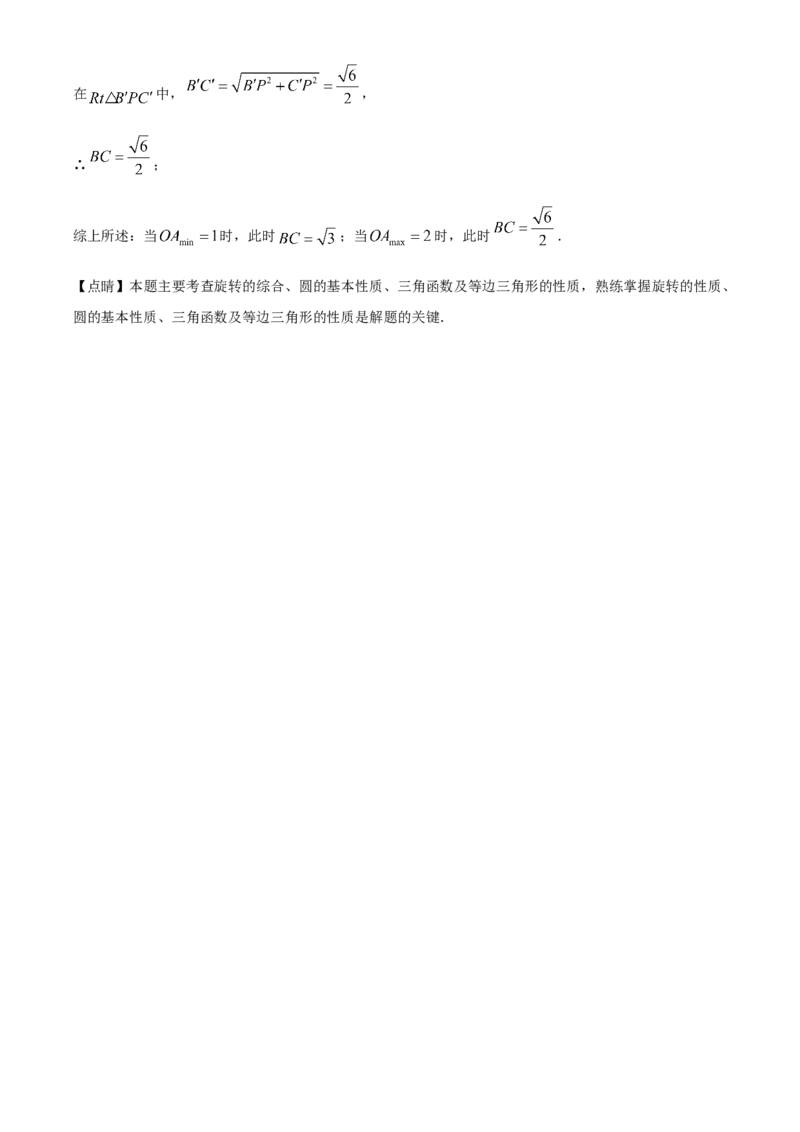文档内容
2021 年北京市中考数学试卷
一、选择题(共16分,每题2分)第1-8题均有四个选项,符合题意的选项只有一个.
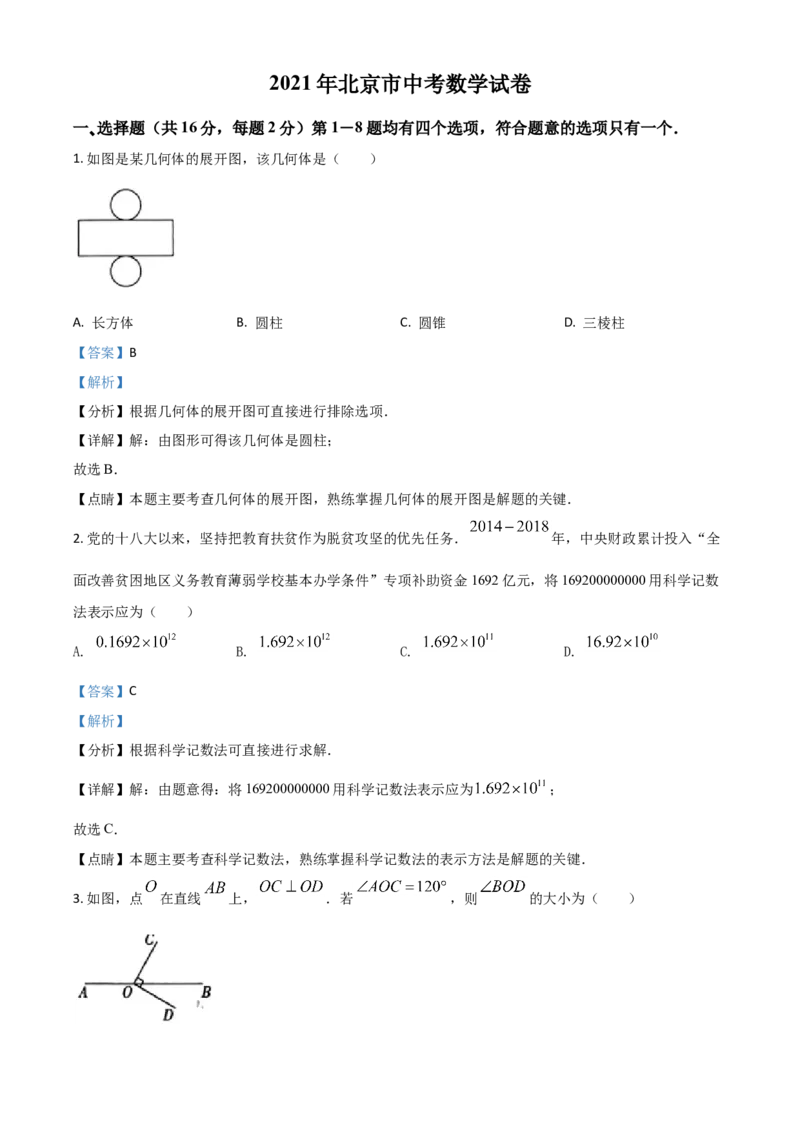
1. 如图是某几何体的展开图,该几何体是( )
A. 长方体 B. 圆柱 C. 圆锥 D. 三棱柱
【答案】B
【解析】
【分析】根据几何体的展开图可直接进行排除选项.
【详解】解:由图形可得该几何体是圆柱;
故选B.
【点睛】本题主要考查几何体的展开图,熟练掌握几何体的展开图是解题的关键.
2. 党的十八大以来,坚持把教育扶贫作为脱贫攻坚的优先任务. 年,中央财政累计投入“全
面改善贫困地区义务教育薄弱学校基本办学条件”专项补助资金1692亿元,将169200000000用科学记数
法表示应为( )
A. B. C. D.
【答案】C
【解析】
【分析】根据科学记数法可直接进行求解.
【详解】解:由题意得:将169200000000用科学记数法表示应为 ;
故选C.
【点睛】本题主要考查科学记数法,熟练掌握科学记数法的表示方法是解题的关键.
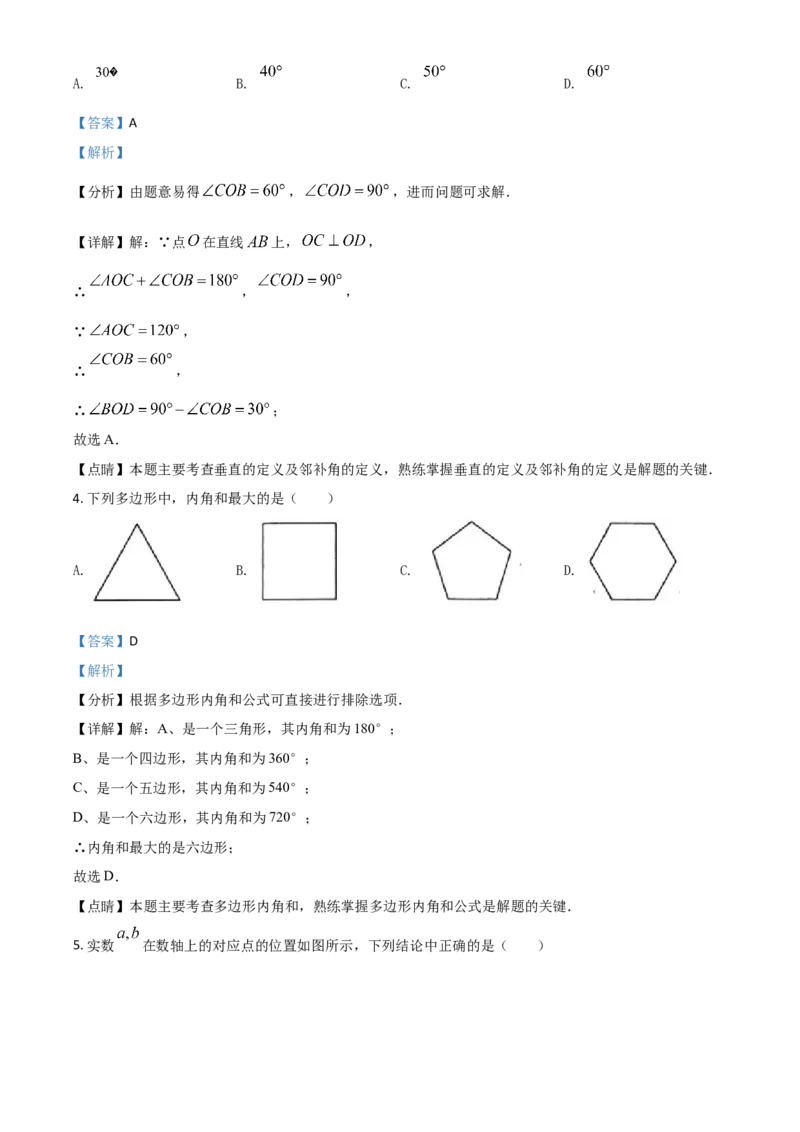
3. 如图,点 在直线 上, .若 ,则 的大小为( )A. B. C. D.
【答案】A
【解析】
【分析】由题意易得 , ,进而问题可求解.
【详解】解:∵点 在直线 上, ,
∴ , ,
∵ ,
∴ ,
∴ ;
故选A.
【点睛】本题主要考查垂直的定义及邻补角的定义,熟练掌握垂直的定义及邻补角的定义是解题的关键.
4. 下列多边形中,内角和最大的是( )
A. B. C. D.
【答案】D
【解析】
【分析】根据多边形内角和公式可直接进行排除选项.
【详解】解:A、是一个三角形,其内角和为180°;
B、是一个四边形,其内角和为360°;
C、是一个五边形,其内角和为540°;
D、是一个六边形,其内角和为720°;
∴内角和最大的是六边形;
故选D.
【点睛】本题主要考查多边形内角和,熟练掌握多边形内角和公式是解题的关键.
5. 实数 在数轴上的对应点的位置如图所示,下列结论中正确的是( )A. B. C. D.
【答案】B
【解析】
【分析】由数轴及题意可得 ,依此可排除选项.
【详解】解:由数轴及题意可得: ,
∴ ,
∴只有B选项正确,
故选B.
【点睛】本题主要考查实数的运算及数轴,熟练掌握实数的运算及数轴是解题的关键.
6. 同时抛掷两枚质地均匀的硬币,则一枚硬币正面向上、一枚硬币反面向上的概率是( )
A. B. C. D.
【答案】C
【解析】
【分析】根据题意可画出树状图,然后进行求解概率即可排除选项.
【详解】解:由题意得:
∴一枚硬币正面向上、一枚硬币反面向上的概率是 ;
故选C.
【点睛】本题主要考查概率,熟练掌握利用树状图求解概率是解题的关键.
的
7. 已知 .若 为整数且 ,则 值为( )
A. 43 B. 44 C. 45 D. 46
【答案】B
【解析】
【分析】由题意可直接进行求解.
【详解】解:∵ ,
∴ ,
∴ ,
∴ ;
故选B.
【点睛】本题主要考查算术平方根,熟练掌握算术平方根是解题的关键.
8. 如图,用绳子围成周长为 的矩形,记矩形的一边长为 ,它的邻边长为 ,矩形的面积为 .
当 在一定范围内变化时, 和 都随 的变化而变化,则 与 与 满足的函数关系分别是( )
A. 一次函数关系,二次函数关系 B. 反比例函数关系,二次函数关系
C. 一次函数关系,反比例函数关系 D. 反比例函数关系,一次函数关系
【答案】A
【解析】
【分析】由题意及矩形的面积及周长公式可直接列出函数关系式,然后由函数关系式可直接进行排除选项.
【详解】解:由题意得:
,整理得: ,
,
∴y与x成一次函数的关系,S与x成二次函数的关系;
故选A.
【点睛】本题主要考查一次函数与二次函数的应用,熟练掌握一次函数与二次函数的应用是解题的关键.二、填空题(共16分,每题2分)
9. 若 在实数范围内有意义,则实数 的取值范围是_______________.
【答案】
【解析】
【分析】根据二次根式有意义的条件可直接进行求解.
【详解】解:由题意得:
,
解得: ;
故答案为 .
【点睛】本题主要考查二次根式有意义的条件,熟练掌握二次根式有意义的条件是解题的关键.
10. 分解因式: ______________.
【答案】
【解析】
【分析】根据提公因式法及平方差公式可直接进行求解.
【详解】解: ;
故答案为 .
【点睛】本题主要考查因式分解,熟练掌握因式分解的方法是解题的关键.
11. 方程 的解为______________.
【答案】
【解析】
【分析】根据分式方程的解法可直接进行求解.
【详解】解:
,∴ ,
经检验: 是原方程 的解.
故答案为:x=3.
【点睛】本题主要考查分式方程的解法,熟练掌握分式方程的解法是解题的关键.
12. 在平面直角坐标系 中,若反比例函数 的图象经过点 和点 ,则 的
值为______________.
【答案】
【解析】
【分析】由题意易得 ,然后再利用反比例函数的意义可进行求解问题.
【详解】解:把点 代入反比例函数 得: ,
∴ ,解得: ,
故答案为-2.
【点睛】本题主要考查反比例函数的图象与性质,熟练掌握反比例函数的图象与性质是解题的关键.
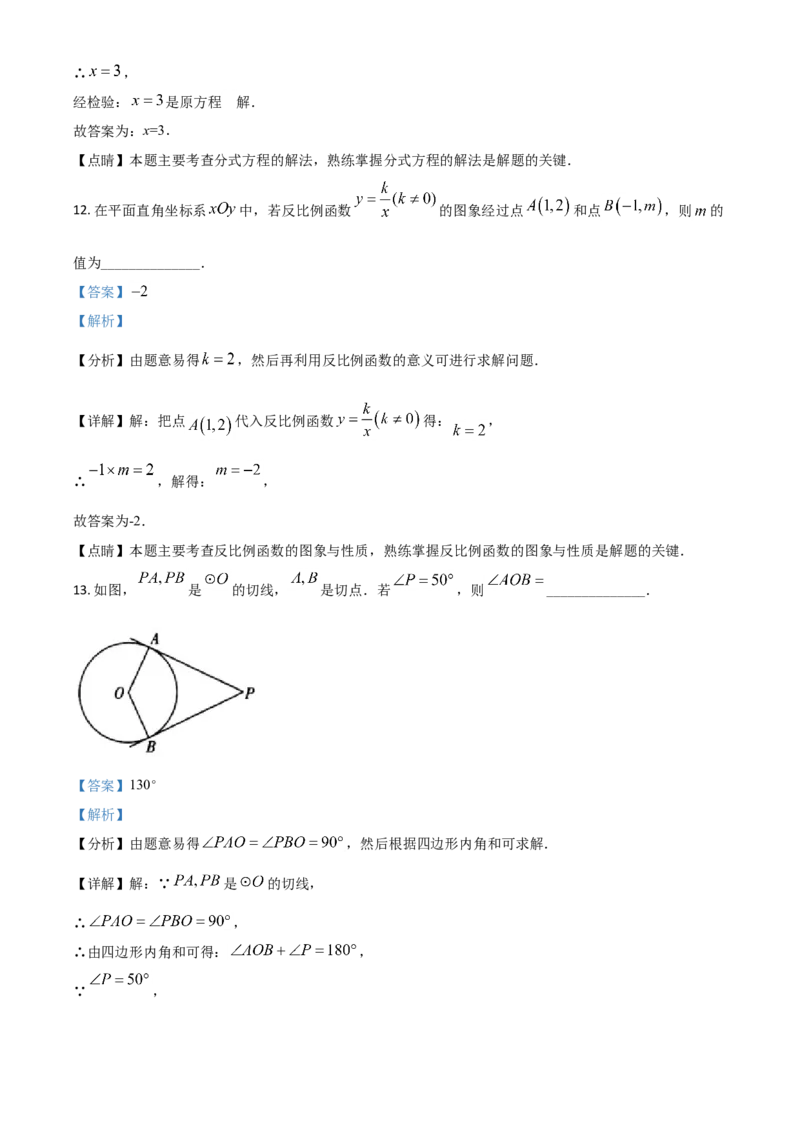
13. 如图, 是 的切线, 是切点.若 ,则 ______________.
【答案】130°
【解析】
【分析】由题意易得 ,然后根据四边形内角和可求解.
【详解】解:∵ 是 的切线,
∴ ,
∴由四边形内角和可得: ,
∵ ,∴ ;
故答案为130°.
【点睛】本题主要考查切线的性质及四边形内角和,熟练掌握切线的性质是解题的关键.
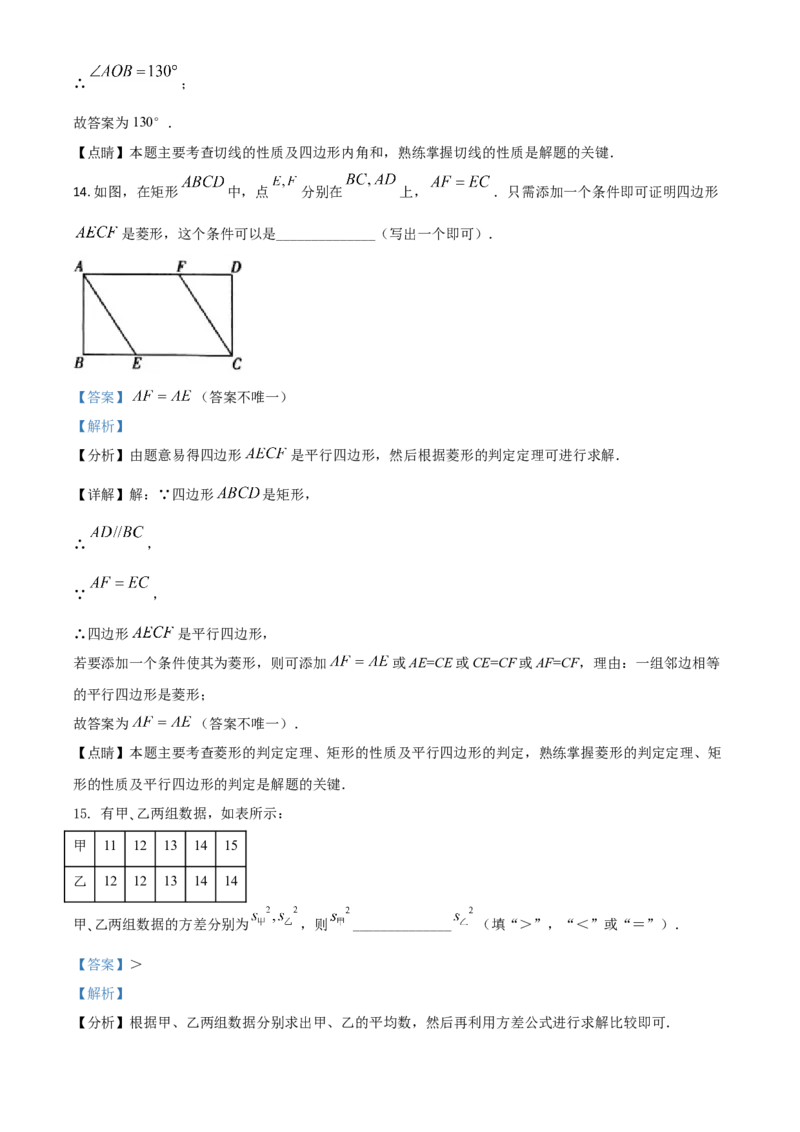
14. 如图,在矩形 中,点 分别在 上, .只需添加一个条件即可证明四边形
是菱形,这个条件可以是______________(写出一个即可).
【答案】 (答案不唯一)
【解析】
【分析】由题意易得四边形 是平行四边形,然后根据菱形的判定定理可进行求解.
【详解】解:∵四边形 是矩形,
∴ ,
∵ ,
∴四边形 是平行四边形,
若要添加一个条件使其为菱形,则可添加 或AE=CE或CE=CF或AF=CF,理由:一组邻边相等
的平行四边形是菱形;
故答案为 (答案不唯一).
【点睛】本题主要考查菱形的判定定理、矩形的性质及平行四边形的判定,熟练掌握菱形的判定定理、矩
形的性质及平行四边形的判定是解题的关键.
15. 有甲、乙两组数据,如表所示:
甲 11 12 13 14 15
乙 12 12 13 14 14
甲、乙两组数据的方差分别为 ,则 ______________ (填“>”,“<”或“=”).
【答案】>
【解析】
【分析】根据甲、乙两组数据分别求出甲、乙的平均数,然后再利用方差公式进行求解比较即可.【详解】解:由题意得:
, ,
∴ ,
,
∴ ,
∴ ;
故答案为>.
【点睛】本题主要考查平均数及方差,熟练掌握平均数及方差的计算是解题的关键.
16. 某企业有 两条加工相同原材料的生产线.在一天内, 生产线共加工 吨原材料,加工时间为
小时;在一天内, 生产线共加工 吨原材料,加工时间为 小时.第一天,该企业将5
吨原材料分配到 两条生产线,两条生产线都在一天内完成了加工,且加工时间相同,则分配到 生
产线的吨数与分配到 生产线的吨数的比为______________.第二天开工前,该企业按第一天的分配结果
分配了5吨原材料后,又给 生产线分配了 吨原材料,给 生产线分配了 吨原材料.若两条生产线都
能在一天内加工完各自分配到的所有原材料,且加工时间相同,则 的值为______________.
【答案】 ①. 2∶3 ②.
【解析】
【分析】设分配到 生产线的吨数为 x 吨,则分配到 B 生产线的吨数为(5-x)吨,依题意可得
, 然 后 求 解 即 可 , 由 题 意 可 得 第 二 天 开 工 时 , 由 上 一 问 可 得 方 程 为,进而求解即可得出答案.
【详解】解:设分配到 生产线 的吨数为x吨,则分配到B生产线的吨数为(5-x)吨,依题意可得:
,解得: ,
∴分配到B生产线的吨数为5-2=3(吨),
∴分配到 生产线的吨数与分配到 生产线的吨数的比为2∶3;
∴第二天开工时,给 生产线分配了 吨原材料,给 生产线分配了 吨原材料,
∵加工时间相同,
∴ ,
解得: ,
∴ ;
故答案为 , .
【点睛】本题主要考查一元一次方程、二元一次方程的应用及比例的基本性质,熟练掌握一元一次方程的
应用及比例的基本性质是解题的关键.
三、解答题(共68分,第17-20题,每题5分,第21-22题,每题6分,第23题5分,第
24题6分,第25题5分,第26题6分,第27-28题,每题7分)解答应写出文字说明、演算
步骤或证明过程.
17. 计算: .
【答案】
【解析】
【分析】根据特殊三角函数值、零次幂及二次根式的运算可直接进行求解.
【详解】解:原式= .
【点睛】本题主要考查特殊三角函数值、零次幂及二次根式的运算,熟练掌握特殊三角函数值、零次幂及
二次根式的运算是解题的关键.18. 解不等式组:
【答案】
【解析】
【分析】根据一元一次不等式组的解法可直接进行求解.
【详解】解:
由①可得: ,
由②可得: ,
∴原不等式组的解集为 .
【点睛】本题主要考查一元一次不等式组的解法,熟练掌握一元一次不等式组的解法是解题的关键.
19. 已知 ,求代数式 的值.
【答案】1
【解析】
【分析】先对代数式进行化简,然后再利用整体思想进行求解即可.
【详解】解:
=
= ,
∵ ,
∴ ,
代入原式得:原式= .
【点睛】本题主要考查整式的乘法运算及完全平方公式,熟练掌握利用整体思想进行整式的化简求值是解
题的关键.
20. 《淮南子・天文训》中记载了一种确定东西方向的方法,大意是:日出时,在地面上点 处立一根杆,
在地面上沿着杆的影子的方向取一点 ,使 两点间的距离为10步(步是古代的一种长度单位),在点 处立一根杆;日落时,在地面上沿着点 处的杆的影子的方向取一点 ,使 两点间的距离为10
步,在点 处立一根杆.取 的中点 ,那么直线 表示的方向为东西方向.
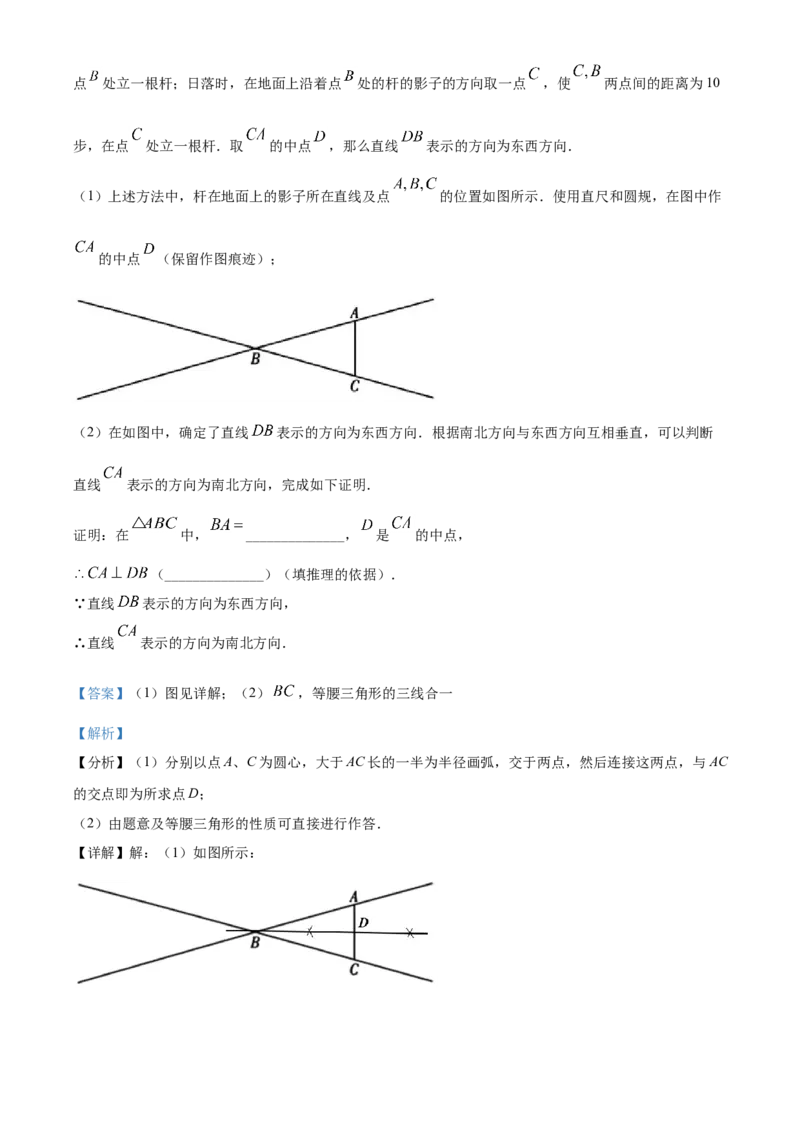
(1)上述方法中,杆在地面上的影子所在直线及点 的位置如图所示.使用直尺和圆规,在图中作
的中点 (保留作图痕迹);
(2)在如图中,确定了直线 表示的方向为东西方向.根据南北方向与东西方向互相垂直,可以判断
直线 表示的方向为南北方向,完成如下证明.
证明:在 中, ______________, 是 的中点,
(______________)(填推理的依据).
∵直线 表示的方向为东西方向,
∴直线 表示的方向为南北方向.
【答案】(1)图见详解;(2) ,等腰三角形的三线合一
【解析】
【分析】(1)分别以点A、C为圆心,大于AC长的一半为半径画弧,交于两点,然后连接这两点,与AC
的交点即为所求点D;
(2)由题意及等腰三角形的性质可直接进行作答.
【详解】解:(1)如图所示:(2)证明:在 中, , 是 的中点,
(等腰三角形的三线合一)(填推理的依据).
∵直线 表示的方向为东西方向,
∴直线 表示的方向为南北方向;
故答案为 ,等腰三角形的三线合一.
【点睛】本题主要考查垂直平分线的尺规作图及等腰三角形的性质,熟练掌握垂直平分线的尺规作图及等
腰三角形的性质是解题的关键.
21. 已知关于 的一元二次方程 .
(1)求证:该方程总有两个实数根;
(2)若 ,且该方程的两个实数根的差为2,求 的值.
【答案】(1)见详解;(2)
【解析】
【分析】(1)由题意及一元二次方程根的判别式可直接进行求证;
(2)设关于 的一元二次方程 的两实数根为 ,然后根据一元二次方程根与系数
的关系可得 ,进而可得 ,最后利用完全平方公式代入求解即可.
【详解】(1)证明:由题意得: ,
∴ ,
∵ ,
∴ ,
∴该方程总有两个实数根;
(2)解:设关于 的一元二次方程 的两实数根为 ,则有:
,∵ ,
∴ ,
解得: ,
∵ ,
∴ .
【点睛】本题主要考查一元二次方程根的判别式及根与系数的关系,熟练掌握一元二次方程根的判别式及
根与系数的关系是解题的关键.
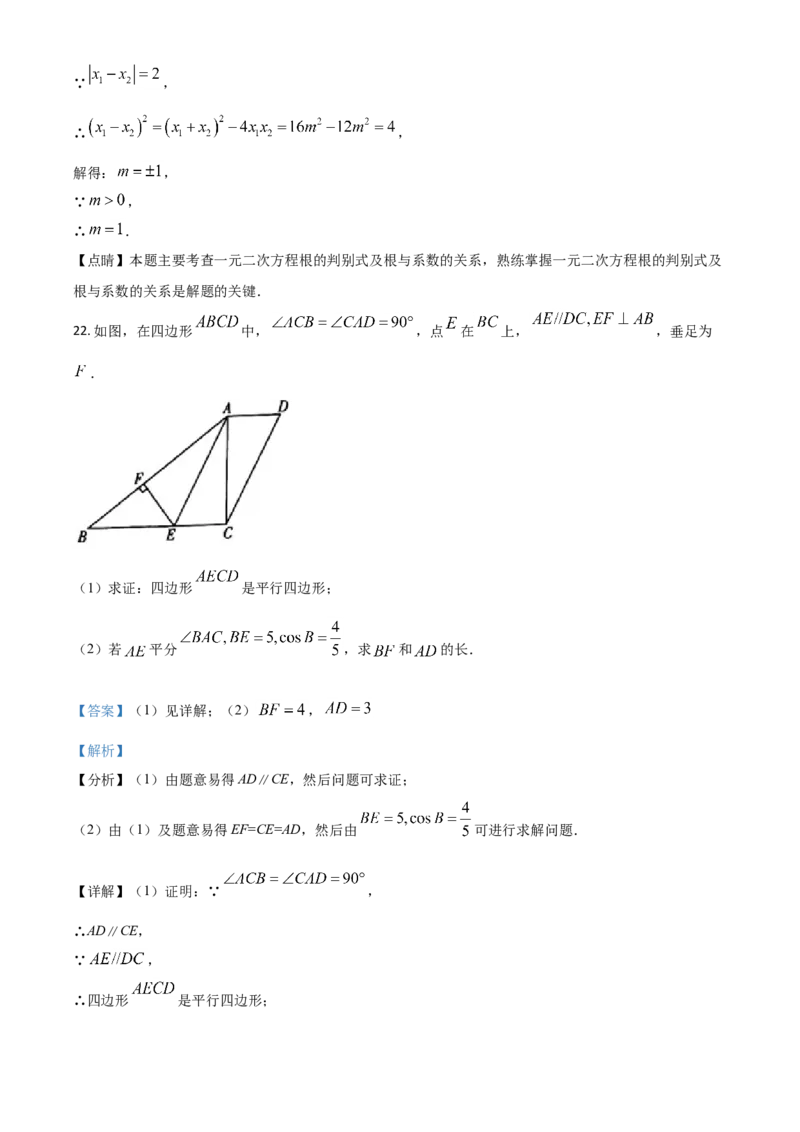
22. 如图,在四边形 中, ,点 在 上, ,垂足为
.
(1)求证:四边形 是平行四边形;
(2)若 平分 ,求 和 的长.
【答案】(1)见详解;(2) ,
【解析】
【分析】(1)由题意易得AD∥CE,然后问题可求证;
(2)由(1)及题意易得EF=CE=AD,然后由 可进行求解问题.
【详解】(1)证明:∵ ,
∴AD∥CE,
∵ ,
∴四边形 是平行四边形;(2)解:由(1)可得四边形 是平行四边形,
∴ ,
∵ , 平分 , ,
∴ ,
∴EF=CE=AD,
∵ ,
∴ ,
∴ ,
∴ .
【点睛】本题主要考查平行四边形的性质与判定、勾股定理、角平分线的性质定理及三角函数,熟练掌握
平行四边形的性质与判定、勾股定理、角平分线的性质定理及三角函数是解题的关键.
23. 在平面直角坐标系 中,一次函数 的图象由函数 的图象向下平移1个单位
长度得到.
(1)求这个一次函数的解析式;
(2)当 时,对于 的每一个值,函数 的值大于一次函数 的值,直接写出
的取值范围.
【答案】(1) ;(2)
【解析】
【分析】(1)由图象的平移及题意可直接求得一次函数的解析式;
(2)由题意可先假设函数 与一次函数 的交点横坐标为 ,则由(1)可得:
,然后结合函数图象可进行求解.【详解】解:(1)由一次函数 的图象由函数 的图象向下平移1个单位长度得到
可得:一次函数的解析式为 ;
(2)由题意可先假设函数 与一次函数 的交点横坐标为 ,则由(1)可得:
,解得: ,
函数图象如图所示:
∴当 时,对于 的每一个值,函数 的值大于一次函数 的值时,根据一次
函数的k表示直线的倾斜程度可得当 时,符合题意,当 时,则函数 与一次函
数 的交点在第一象限,此时就不符合题意,
综上所述: .
【点睛】本题主要考查一次函数的图象与性质,熟练掌握一次函数的图象与性质是解题的关键.
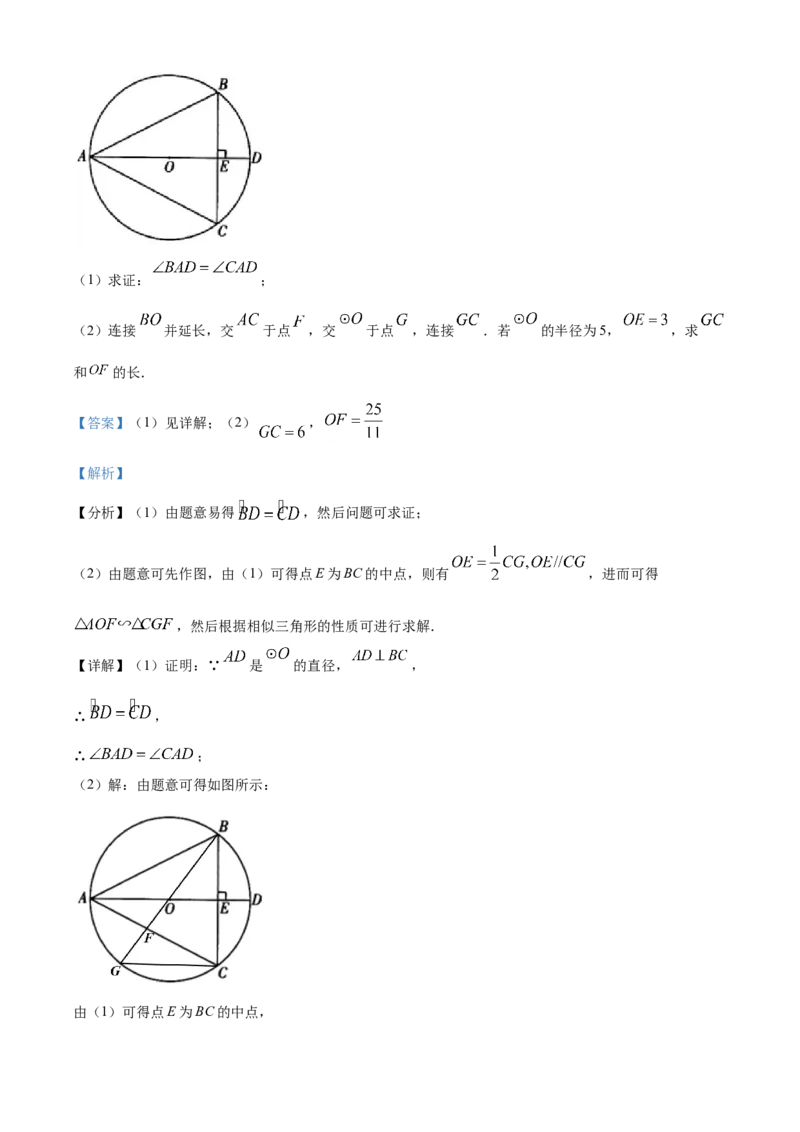
24. 如图, 是 的外接圆, 是 的直径, 于点 .(1)求证: ;
(2)连接 并延长,交 于点 ,交 于点 ,连接 .若 的半径为5, ,求
和 的长.
【答案】(1)见详解;(2) ,
【解析】
【分析】(1)由题意易得 ,然后问题可求证;
(2)由题意可先作图,由(1)可得点E为BC的中点,则有 ,进而可得
,然后根据相似三角形的性质可进行求解.
【详解】(1)证明:∵ 是 的直径, ,
∴ ,
∴ ;
(2)解:由题意可得如图所示:
由(1)可得点E为BC的中点,∵点O是BG的中点,
∴ ,
∴ ,
∴ ,
∵ ,
∴ ,
∵ 的半径为5,
∴ ,
∴ ,
∴ .
【点睛】本题主要考查垂径定理、三角形中位线及相似三角形的性质与判定,熟练掌握垂径定理、三角形
中位线及相似三角形的性质与判定是解题的关键.
25. 为了解甲、乙两座城市的邮政企业4月份收入的情况,从这两座城市的邮政企业中,各随机抽取了25家
邮政企业,获得了它们4月份收入(单位:百万元)的数据,并对数据进行整理、描述和分析.下面给出了
部分信息.
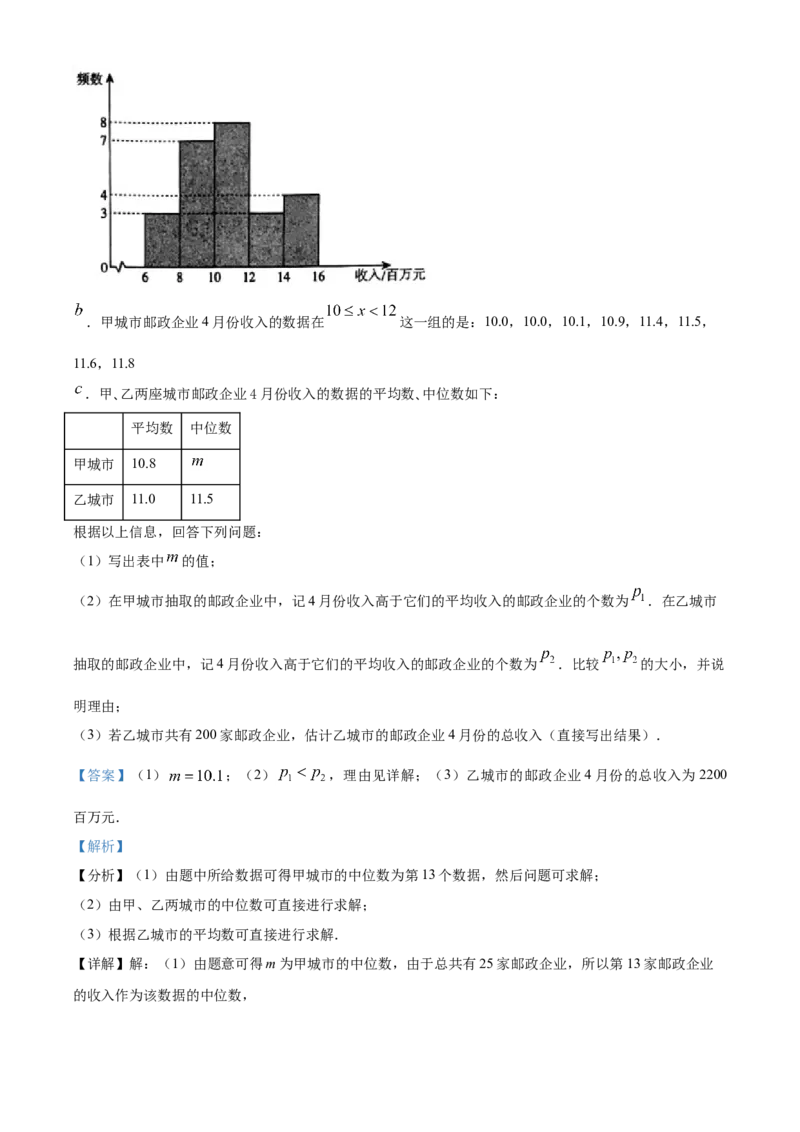
.甲城市邮政企业4月份收入的数据的频数分布直方图如下(数据分成5组:
):.甲城市邮政企业4月份收入的数据在 这一组的是:10.0,10.0,10.1,10.9,11.4,11.5,
11.6,11.8
.甲、乙两座城市邮政企业4月份收入的数据的平均数、中位数如下:
平均数 中位数
甲城市 10.8
乙城市 11.0 11.5
根据以上信息,回答下列问题:
(1)写出表中 的值;
(2)在甲城市抽取的邮政企业中,记4月份收入高于它们的平均收入的邮政企业的个数为 .在乙城市
抽取的邮政企业中,记4月份收入高于它们的平均收入的邮政企业的个数为 .比较 的大小,并说
明理由;
(3)若乙城市共有200家邮政企业,估计乙城市的邮政企业4月份的总收入(直接写出结果).
【答案】(1) ;(2) ,理由见详解;(3)乙城市的邮政企业4月份的总收入为2200
百万元.
【解析】
【分析】(1)由题中所给数据可得甲城市的中位数为第13个数据,然后问题可求解;
(2)由甲、乙两城市的中位数可直接进行求解;
(3)根据乙城市的平均数可直接进行求解.
【详解】解:(1)由题意可得m为甲城市的中位数,由于总共有25家邮政企业,所以第13家邮政企业
的收入作为该数据的中位数,∵ 有3家, 有7家, 有8家,
∴中位数落在 上,
∴ ;
为
(2)由(1)可得:甲城市中位数低于平均数,则 最大 12个;乙城市中位数高于平均数,则 至少
为13个,
∴ ;
(3)由题意得:
(百万元);
答:乙城市的邮政企业4月份的总收入为2200百万元.
【点睛】本题主要考查中位数、平均数及统计与调查,熟练掌握中位数、平均数及统计与调查是解题的关
键.
26. 在平面直角坐标系 中,点 和点 在抛物线 上.
(1)若 ,求该抛物线的对称轴;
(2)已知点 在该抛物线上.若 ,比较 的大小,并说明理由.
【答案】(1) ;(2) ,理由见解析
【解析】
【分析】(1)由题意易得点 和点 ,然后代入抛物线解析式进行求解,最后根据对称轴公式进
行求解即可;
(2)由题意可分当 时和当 时,然后根据二次函数的性质进行分类求解即可.
【详解】解:(1)当 时,则有点 和点 ,代入二次函数 得:
,解得: ,
∴抛物线解析式为 ,∴抛物线的对称轴为 ;
(2)由题意得:抛物线 始终过定点 ,则由 可得:
①当 时,由抛物线 始终过定点 可得此时的抛物线开口向下,即
,与 矛盾;
②当 时,
∵抛物线 始终过定点 ,
∴此时抛物线的对称轴的范围为 ,
∵点 在该抛物线上,
∴它们离抛物线对称轴的距离的范围分别为 ,
∵ ,开口向上,
∴由抛物线的性质可知离对称轴越近越小,
∴ .
【点睛】本题主要考查二次函数的综合,熟练掌握二次函数的图象与性质是解题的关键.
27. 如图,在 中, 为 的中点,点 在 上,以点 为中心,将线
段 顺时针旋转 得到线段 ,连接 .
(1)比较 与 的大小;用等式表示线段 之间的数量关系,并证明;(2)过点 作 的垂线,交 于点 ,用等式表示线段 与 的数量关系,并证明.
【答案】(1) , ,理由见详解;(2) ,理由见详解.
【解析】
【分析】(1)由题意及旋转的性质易得 , ,然后可证 ,
进而问题可求解;
(2)过点E作EH⊥AB,垂足为点Q,交AB于点H,由(1)可得 , ,易证
,进而可得 ,然后可得 ,最后根据相似三角形的性质可求
证.
【详解】(1)证明:∵ ,
∴ ,
∴ ,
由旋转的性质可得 ,
∵ ,
∴ ,
∴ ,
∵点M为BC的中点,
∴ ,
∵ ,
∴ ;
(2)证明: ,理由如下:
过点E作EH⊥AB,垂足为点Q,交AB于点H,如图所示:∴ ,
由(1)可得 ,
∴ , ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∵ ,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,
∴ .
【点睛】本题主要考查全等三角形的性质与判定、相似三角形的性质与判定及等腰三角形的性质、旋转的
性质,熟练掌握全等三角形的性质与判定、相似三角形的性质与判定及等腰三角形的性质、旋转的性质是
解题的关键.
28. 在平面直角坐标系 中, 的半径为1,对于点 和线段 ,给出如下定义:若将线段 绕点 旋转可以得到 的弦 ( 分别是 的对应点),则称线段 是 的以点 为中心
的“关联线段”.
(1)如图,点 的横、纵坐标都是整数.在线段 中, 的以点
为中心的“关联线段”是______________;
(2) 是边长为1的等边三角形,点 ,其中 .若 是 的以点 为中心的“关联
线段”,求 的值;
(3)在 中, .若 是 的以点 为中心的“关联线段”,直接写出 的最小
值和最大值,以及相应的 长.
【答案】(1) ;(2) ;(3)当 时,此时 ;当 时,此时
.
【解析】
【分析】(1)以点A为圆心,分别以 为半径画圆,进而观察是否与 有
交点即可;
(2)由旋转的性质可得 是等边三角形,且 是 的弦,进而画出图象,则根据等边三角形
的性质可进行求解;(3)由 是 的以点 为中心的“关联线段”,则可知 都在 上,且
,然后由题意可根据图象来进行求解即可.
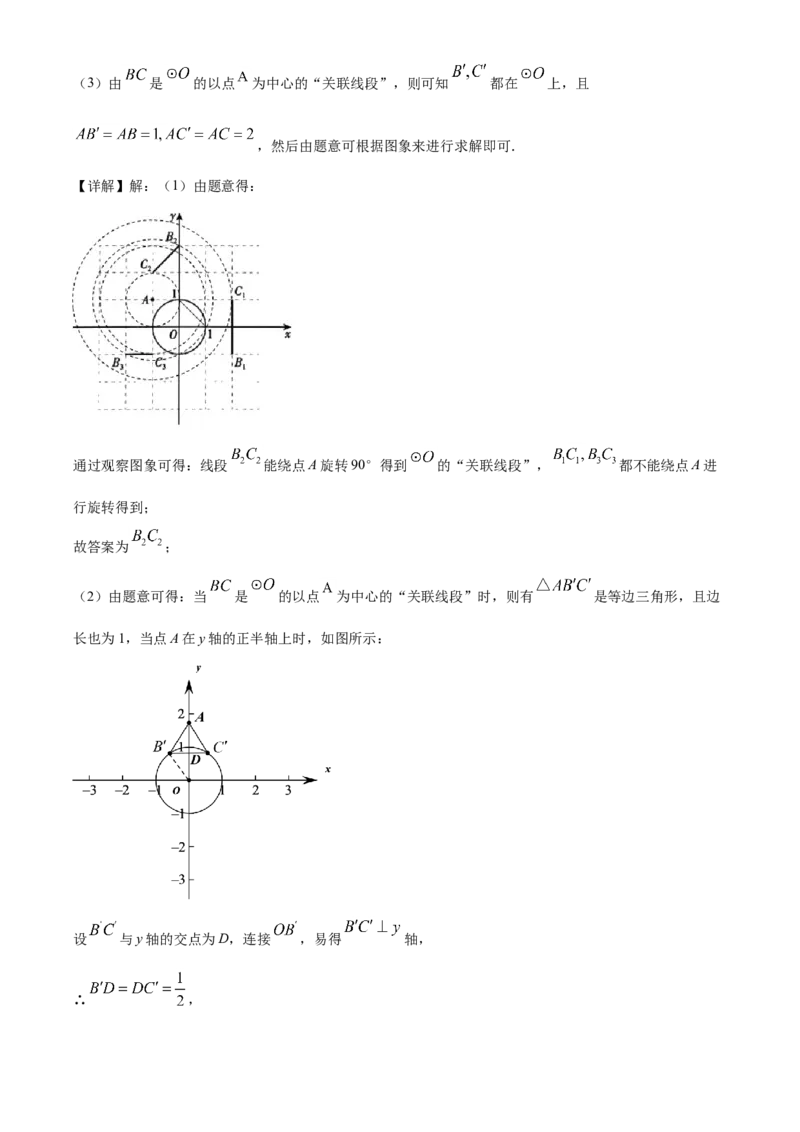
【详解】解:(1)由题意得:
通过观察图象可得:线段 能绕点A旋转90°得到 的“关联线段”, 都不能绕点A进
行旋转得到;
故答案为 ;
(2)由题意可得:当 是 的以点 为中心的“关联线段”时,则有 是等边三角形,且边
长也为1,当点A在y轴的正半轴上时,如图所示:
设 与y轴的交点为D,连接 ,易得 轴,
∴ ,∴ , ,
∴ ,
∴ ;
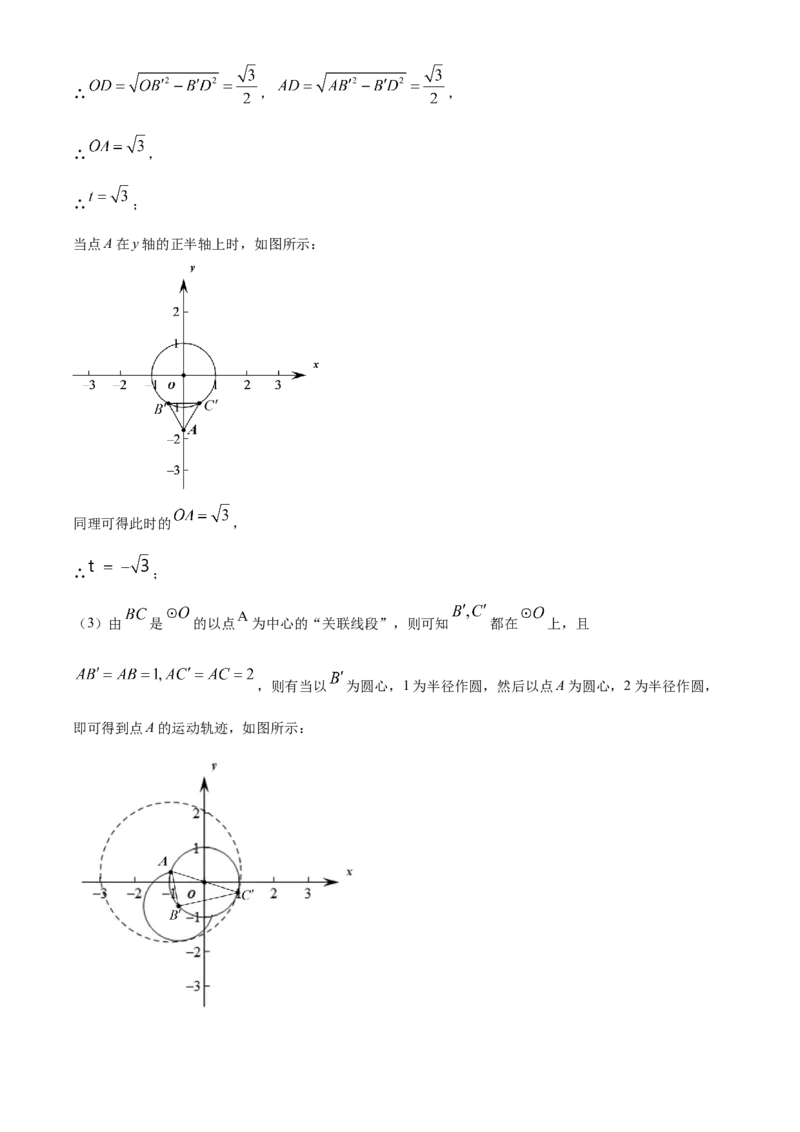
当点A在y轴的正半轴上时,如图所示:
同理可得此时的 ,
∴ ;
(3)由 是 的以点 为中心的“关联线段”,则可知 都在 上,且
,则有当以 为圆心,1为半径作圆,然后以点A为圆心,2为半径作圆,
即可得到点A的运动轨迹,如图所示:由运动轨迹可得当点A也在 上时为最小,最小值为1,此时 为 的直径,
∴ ,
∴ ,
∴ ;
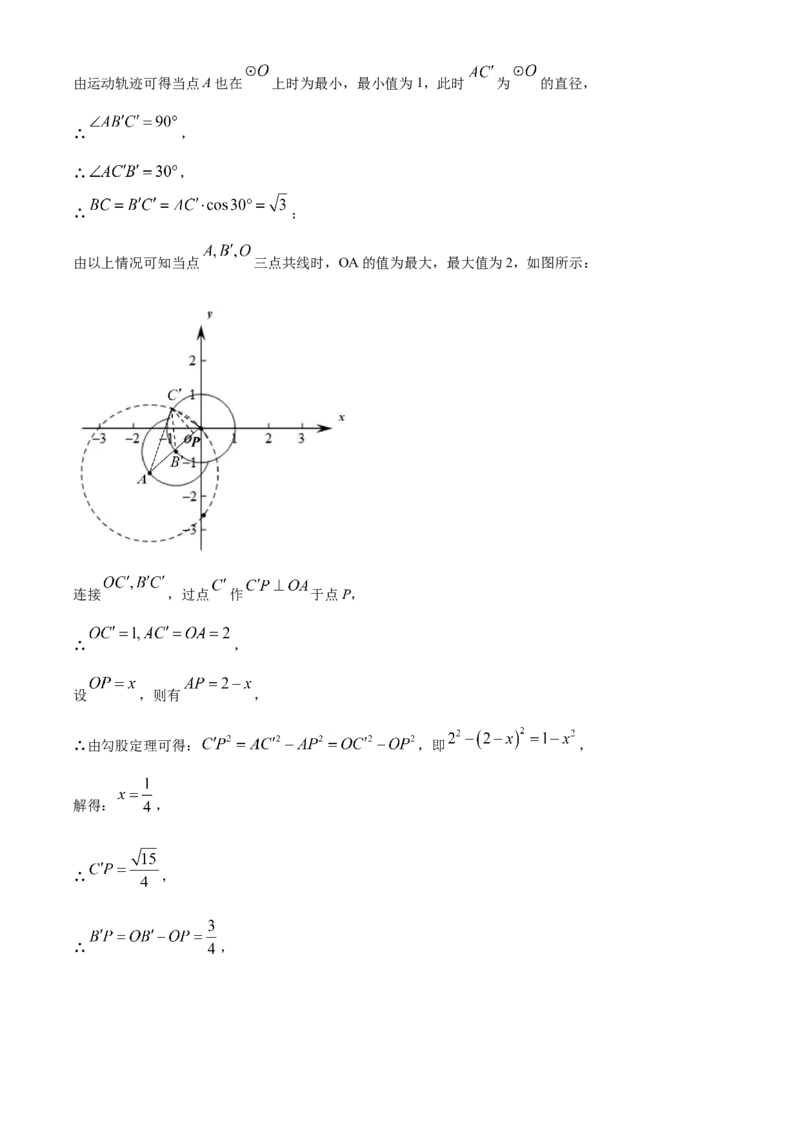
由以上情况可知当点 三点共线时,OA的值为最大,最大值为2,如图所示:
连接 ,过点 作 于点P,
∴ ,
设 ,则有 ,
∴由勾股定理可得: ,即 ,
解得: ,
∴ ,
∴ ,在 中, ,
∴ ;
综上所述:当 时,此时 ;当 时,此时 .
【点睛】本题主要考查旋转的综合、圆的基本性质、三角函数及等边三角形的性质,熟练掌握旋转的性质、
圆的基本性质、三角函数及等边三角形的性质是解题的关键.