数学（新高考Ⅱ卷）（全解全析）_2023高考押题卷_学易金卷-2023学科网押题卷（各科各版本）_2023学科网押题卷-学易金卷-数学_数学（新高考Ⅱ卷）-学易金卷：2023年高考考前押题密卷

2023 年高考考前押题密卷 数学·全解全析 一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个选项是符 合题目要求的． 1．【改编】设集合 ，则 （ ） A． B． C． D． 【答案】B 【解析】由题设可得 ，故 ，故选：B. 2．已知 ， 为虚数单位，则 （ ） A． B． C． D． 【答案】C 【解析】因为 ，则 .故选：C. 3．将向量 绕坐标原点O顺时针旋转 得到 ，则 （ ） A．0 B． C．2 D． 【答案】D 【解析】根据题意可知 ．故选：D 4．黄地绿彩云龙纹盘是收藏于中国国家博物馆的一件明代国宝级瓷器.该龙纹盘敞口，弧壁，广底，圈足. 器内施白釉，外壁以黄釉为地，刻云龙纹并填绿彩，美不胜收.黄地绿彩云龙纹盘可近似看作是圆台和圆柱 的组合体，其口径22.5cm，足径14.4cm，高3.8cm，其中底部圆柱高0.8cm，则黄地绿彩云龙纹盘的侧面 积约为（ ）（附：圆台的侧面积 ， ， 为两底面半径， 为母线长，其中 的值取3， ） A． B． C． D． 【答案】A 【解析】设该圆台的母线长为 ，两底面圆半径分别为 ， （其中 ）， 则 ， ， ， 所以 ， 故圆台部分的侧面积为 ， 圆柱部分的侧面积为 ， 故该黄地绿彩云龙纹盘的侧面积约为 .故选：A. 5．某病毒暴发，全省支援，需要从我市某医院某科室的4名男医生（含一名主任医师）､5名女医生（含 一名主任医师）中分别选派3名男医生和2名女医生，则在有一名主任医师被选派的条件下，两名主任医 1 学科网（北京）股份有限公司师都被选派的概率为（ ） A． B． C． D． 【答案】D 【解析】记“选派3名男医生和2名女医生，有一名主任医生被选派”为事件A， 则 ， 记“选派3名男医生和2名女医生，两名主任医师都被选派”为事件B, 则 ，故选：D 6．已知 ，且 ，则 （ ） A． B． C． D． 【答案】A 【解析】因为 ，所以 ， 即 ，所以 ， 所以 ，解得 或 ， 因为 ，所以 ， 所以 .故选：A 7．已知 ， ， ，则（ ） A． B． C． D 【答案】C 【解析】设 ，求导 ，所以当 时， ， 单调递增， 故 ，即 ，所以 ； 设 ，求导 ， 所以当 时， ， 单调递增， 2 学科网（北京）股份有限公司，所以 ，故 .故选：C 8．已知函数 及其导函数 定义域均为R，满足 ，记 ，其导 函数为 且 的图象关于原点对称，则 （ ） A．0 B．1 C．4 D．3 【答案】B 【解析】由 关于原点对称，则 关于 轴对称，且 ， 所以 关于 对称， 关于 对称，且 ， 又 ，即 ，则 关于 对称， 综上， ， ，则 ， 所以 ，而 ，故 ， 又 ，则 关于 对称，即 ， 所以 ，则 ， 所以 .故选：B 二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求， 全部选对的得5分，部分选对的得2分，有选错的得0分． 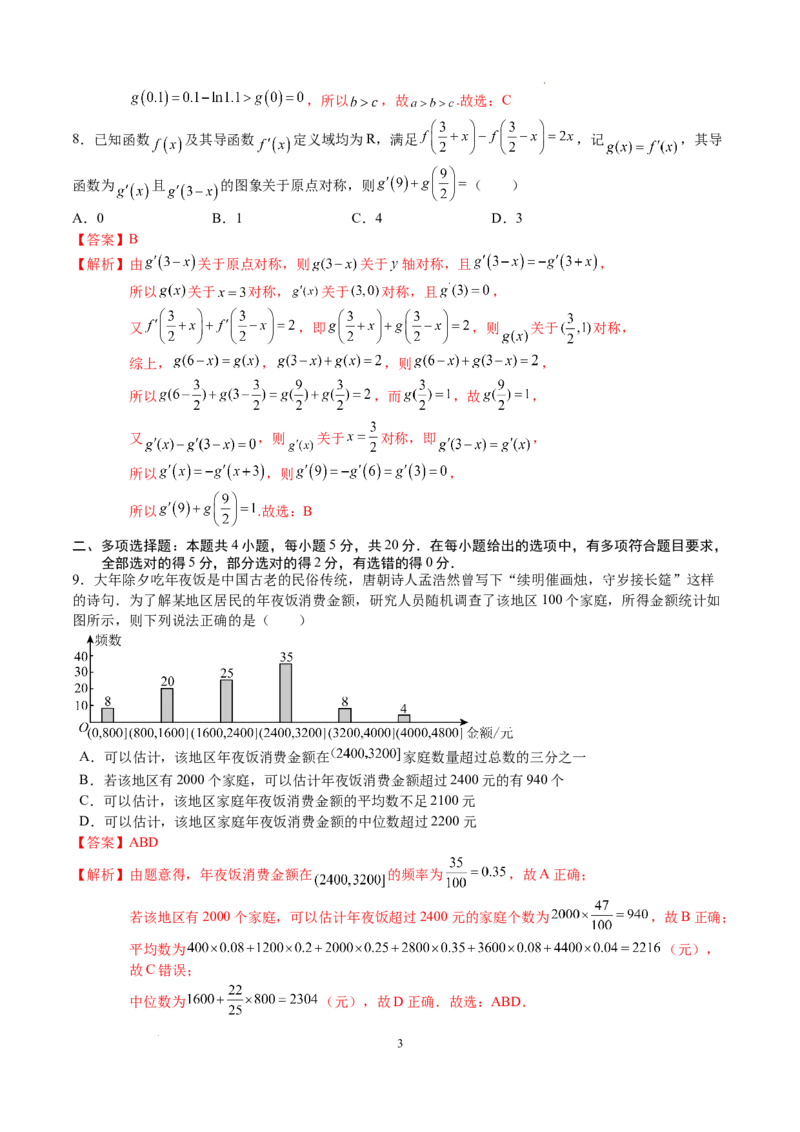9．大年除夕吃年夜饭是中国古老的民俗传统，唐朝诗人孟浩然曾写下“续明催画烛，守岁接长筵”这样 的诗句．为了解某地区居民的年夜饭消费金额，研究人员随机调查了该地区100个家庭，所得金额统计如 图所示，则下列说法正确的是（ ） A．可以估计，该地区年夜饭消费金额在 家庭数量超过总数的三分之一 B．若该地区有2000个家庭，可以估计年夜饭消费金额超过2400元的有940个 C．可以估计，该地区家庭年夜饭消费金额的平均数不足2100元 D．可以估计，该地区家庭年夜饭消费金额的中位数超过2200元 【答案】ABD 【解析】由题意得，年夜饭消费金额在 的频率为 ，故A正确； 若该地区有2000个家庭，可以估计年夜饭超过2400元的家庭个数为 ，故B正确； 平均数为 （元）， 故C错误； 中位数为 （元），故D正确．故选：ABD． 3 学科网（北京）股份有限公司10．已知双曲线 的左、右焦点分别为 ， ，抛物线 的焦点与双曲线 的焦 点重合，点 是这两条曲线的一个公共点，则下列说法正确的是（ ） A．双曲线 的渐近线方程为 B． C． 的面积为 D． 【答案】AB 【解析】由已知，抛物线的焦点坐标为 ，所以双曲线右焦点 ，即 . 又 ，所以 ，所以，双曲线的方程为 . 对于A项，双曲线的 的渐近线方程为 ，故A项正 确； 对于B项，联立双曲线与抛物线的方程 ， 整理可得， ，解得 或 （舍去负值）， 所以 ，代入 可得， . 设 ，又 ，所以 ，故B项正确； 对于C项，易知 ，故C项错误； 对于D项，因为 ， 所以，由余弦定理可得， ，故D项错误. 故选：AB. 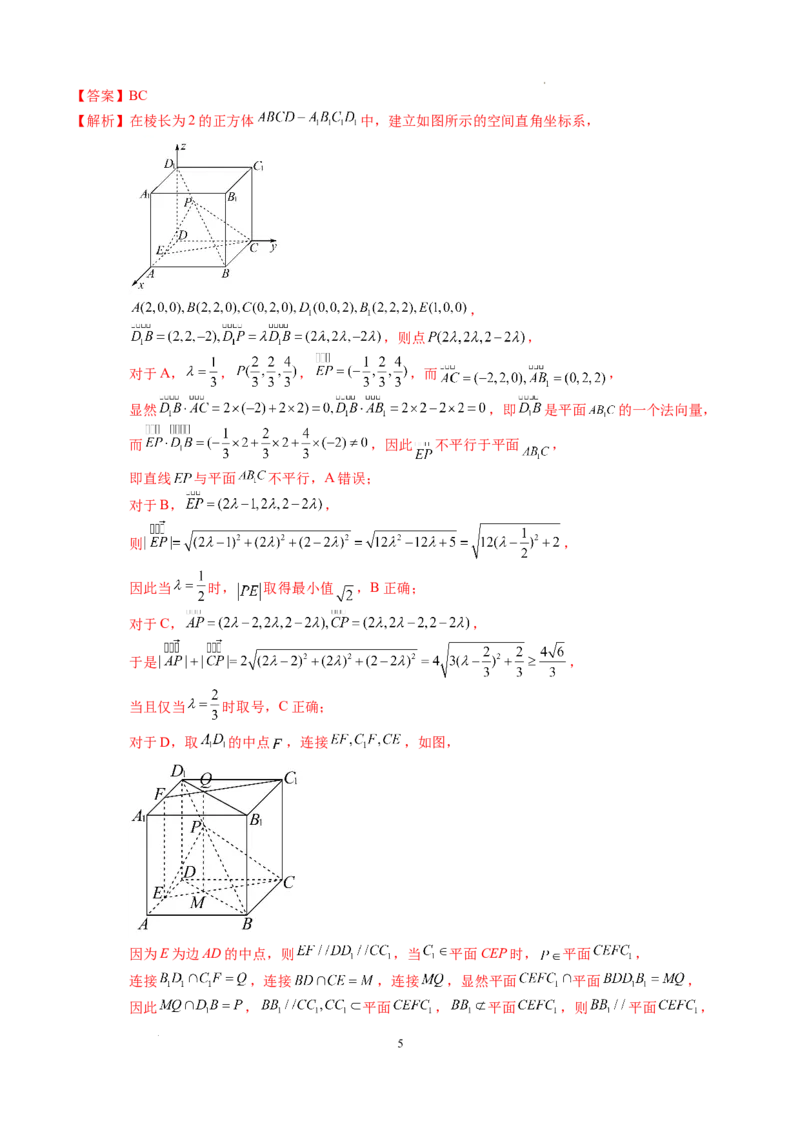11．如图，在棱长为2的正方体 中，E为边AD的中点，点P为线段 上的动点，设 ，则（ ） A．当 时，EP//平面 B．当 时， 取得最小值，其值为 C． 的最小值为 D．当 平面CEP时， 4 学科网（北京）股份有限公司【答案】BC 【解析】在棱长为2的正方体 中，建立如图所示的空间直角坐标系， ， ，则点 ， 对于A， ， ， ，而 ， 显然 ，即 是平面 的一个法向量， 而 ，因此 不平行于平面 ， 即直线 与平面 不平行，A错误； 对于B， ， 则 ， 因此当 时， 取得最小值 ，B正确； 对于C， ， 于是 ， 当且仅当 时取号，C正确； 对于D，取 的中点 ，连接 ，如图， 因为E为边AD的中点，则 ，当 平面CEP时， 平面 ， 连接 ，连接 ，连接 ，显然平面 平面 ， 因此 ， 平面 ， 平面 ，则 平面 ， 5 学科网（北京）股份有限公司即有 ，而 ，所以 ，D错误.故选：BC 12．记 、 分别为函数 、 的导函数，若存在 ，满足 且 ，则称 为函数 与 的一个“ 点”，则下列说法正确的为（ ） A．函数 与 存在唯一“ 点” B．函数 与 存在两个“ 点” C．函数 与 不存在“ 点” D．若函数 与 存在“ 点”，则 【答案】ACD 【解析】令 . 对于A选项， ，则 ， 由 可得 ，由 可得 ， 所以，函数 在 上单调递减，在 上单调递增， 所以， ，所以， ， 此时，函数 与 存在唯一“ 点”，A对； 对于B选项， ，则 ， 函数 的定义域为 ，令 可得 ，且 ， 所以，函数 与 不存在“ 点”，B错； 对于C选项， ，则 ， 令 可得 ，解得 或 ，但 ， ， 此时，函数 与 不存在“ 点”，C对； 对于D选项， ，其中 ，则 ， 若函数 与 存在“ 点”，记为 ， 则 ，解得 ，D对.故选：ACD. 三、填空题：本题共4小题，每小题5分，共20分． 13．【改编】在 的展开式中x的系数为______． 【答案】 6 学科网（北京）股份有限公司【解析】 的展开式中x的项为 ， 所以展开式中 的系数为 ． 故答案为： . 14．曲线 在点 处的切线方程为___________. 【答案】 【解析】因为 ， 所以 ， 所以切线方程为： ，即： . 故答案为： . 15．已知圆 及圆 ，若圆 上任意一点 ，圆 上均存在一点 使得 ，则实数 的取值范围是______. 【答案】 【解析】由 ，即 在 上运动，而 为圆 上任意一点， 要使圆 上存在一点 使 ， 即过 点相互垂直的两直线与圆 有交点且 与两条垂线的夹角均为 即可， 所以，只需 为射线 与圆 交点时， 使过 点相互垂直的两直线与圆 有交点且 与两条垂线的夹角均为 ， 如上图，上述两条垂线刚好与圆 相切为满足要求的临界情况， 所以，只需 ， 为圆 半径，即 ， 又 ，故 ，可得 . 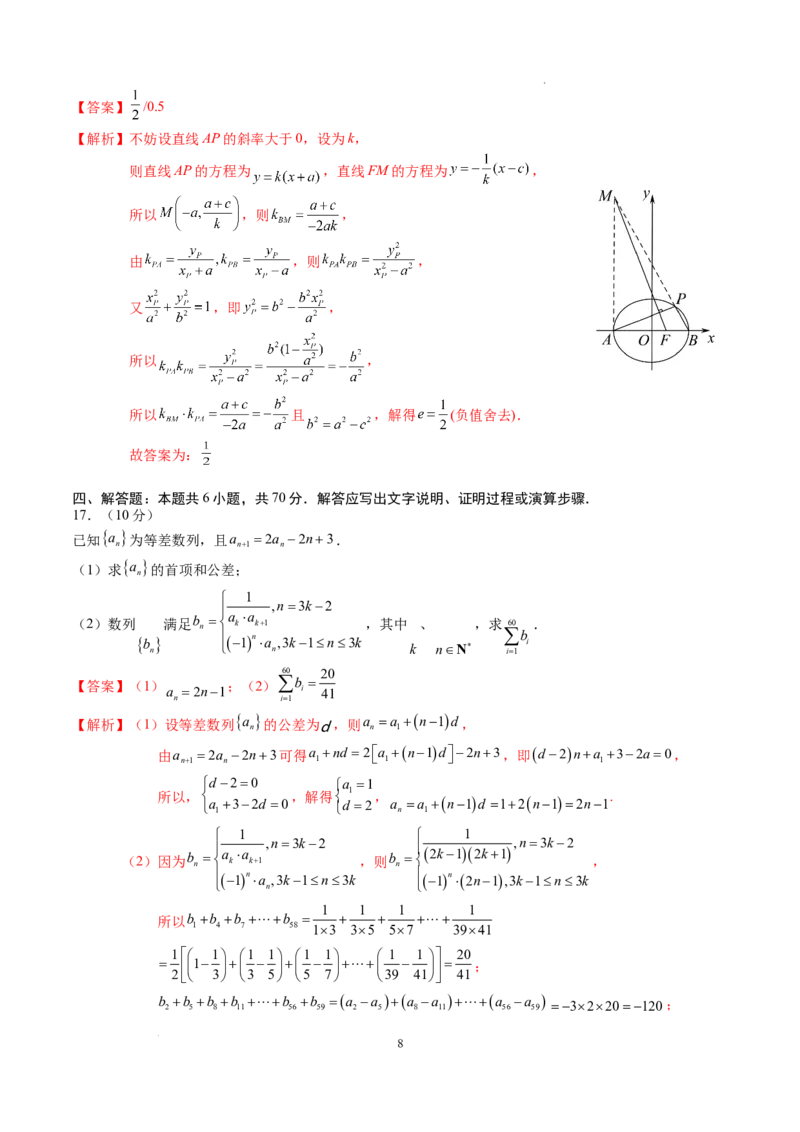故答案为： 微信搜索“高中试卷君”公众号 领取押题卷联考卷 16．已知椭圆 的右焦点为F，左右顶点分别为A，B，点P是椭圆G上异于A，B的动 点，过F作直线AP的垂线交直线BP于点 ，若 ，则椭圆G的离心率为__________． 7 学科网（北京）股份有限公司【答案】 /0.5 【解析】不妨设直线AP的斜率大于0，设为k， 则直线AP的方程为 ，直线FM的方程为 ， 所以 ，则 ， 由 ，则 ， 又 ，即 ， 所以 ， 所以 且 ，解得 (负值舍去)． 故答案为： 四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（10分） 已知 a  为等差数列，且a 2a 2n3． n n1 n （1）求 a  的首项和公差； n  1 ,n3k2  （2）数列 b n  满足b n     a  k 1   a n k  1 a n ,3k1n3k ，其中 k 、 nN ，求  i 6  0 1 b i ． 60 20 【答案】（1） ；（2） b  a 2n1 i 41 n i1 【解析】（1）设等差数列 a n  的公差为d，则a n a 1 n1d， 由a n1 2a n 2n3可得a 1 nd 2  a 1 n1d  2n3，即d2na 1 32a0， d20 a 1 所以， ，解得 1 ， . a 1 32d 0 d 2 a n a 1 n1d 12n12n1  1  1 ,n3k2 ,n3k2 （2）因为b n    a k a k1 ，则b n    2k12k1 ， 1n a ,3k1n3k  1n 2n1,3k1n3k  n  1 1 1 1 所以b b b b     1 4 7 58 13 35 57 3941 1 1 1 1 1 1  1 1  20  1         ； 2 3 3 5 5 7 39 41 41 b 2 b 5 b 8 b 11 b 56 b 59 a 2 a 5 a 8 a 11 a 56 a 59  3220120； 8 学科网（北京）股份有限公司b 3 b 6 b 9 b 12 b 57 b 60 a 3 a 6 a 9 a 12 a 57 a 60  3220120. 60 因此， b b b b b b b b b b b b b  i 1 4 7 58 2 5 8 59 3 6 9 60 i1 20 20  120120 . 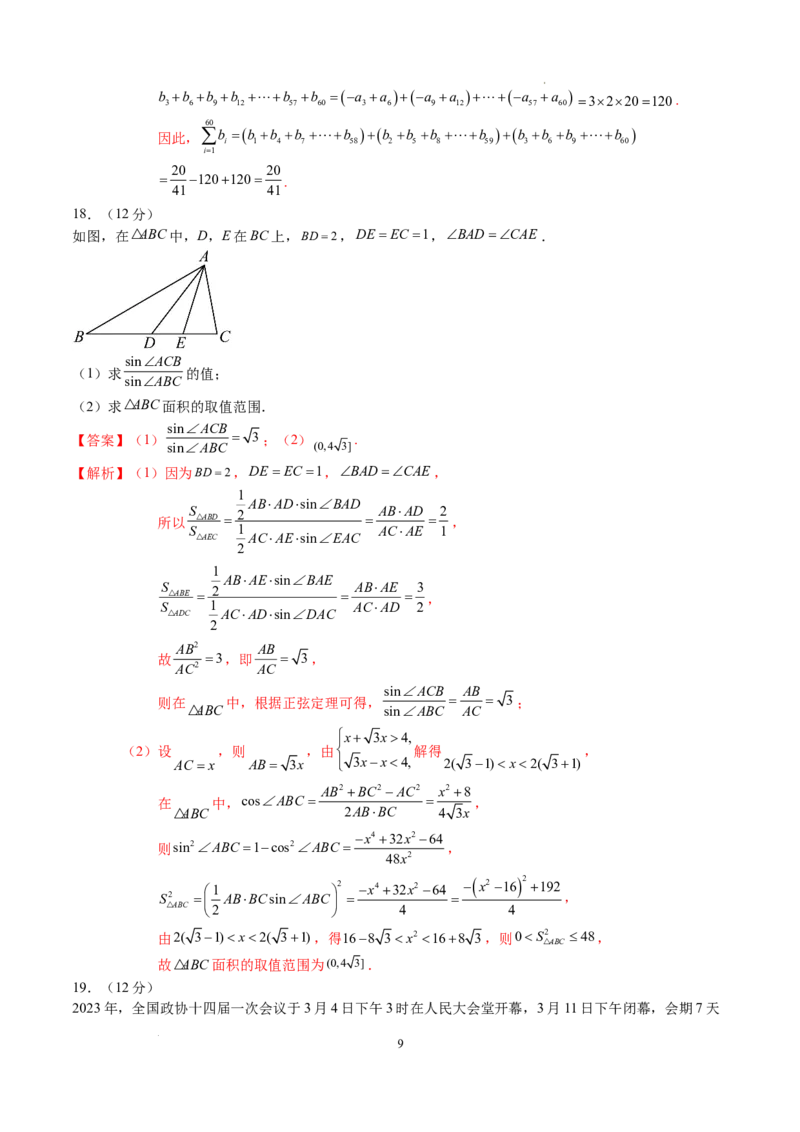41 41 18．（12分） 如图，在ABC中，D，E在BC上，BD2，DEEC 1，BADCAE． sinACB （1）求 的值； sinABC （2）求ABC面积的取值范围． sinACB 【答案】（1）  3；（2） . sinABC (0,4 3] 【解析】（1）因为BD2，DEEC 1，BADCAE， 1 ABADsinBAD S 2 ABAD 2 所以 ABD    ， S 1 ACAE 1 AEC ACAEsinEAC 2 1 ABAEsinBAE S 2 ABAE 3 ABE    ， S 1 ACAD 2 ADC ACADsinDAC 2 AB2 AB 故 3，即  3， AC2 AC sinACB AB 则在 中，根据正弦定理可得，   3； ABC sinABC AC  x 3x4, （2）设 ，则 ，由 解得 ， AC x AB 3x  3xx4, 2( 31)x2( 31) AB2BC2AC2 x28 在 中，cosABC   ， ABC 2ABBC 4 3x x432x264 则sin2ABC 1cos2ABC  ， 48x2 1  2 x432x264   x216 2 192 S2  ABBCsinABC   ， ABC 2  4 4 由2( 31)x2( 31)，得168 3x2 168 3，则0S2 48， ABC 故ABC面积的取值范围为(0,4 3]． 19．（12分） 2023年，全国政协十四届一次会议于3月4日下午3时在人民大会堂开幕，3月11日下午闭幕，会期7天 9 学科网（北京）股份有限公司半；十四届全国人大一次会议于3月5日上午开幕，13日上午闭幕，会期8天半.为调查学生对两会相关知 识的了解情况，某高中学校开展了两会知识问答活动，现从全校参与该活动的学生中随机抽取320名学生， 他们的得分（满分100分）的频率分布折线图如下. （1）若此次知识问答的得分X N  ,2 ，用样本来估计总体，设，分别为被抽取的320名学生得 分的平均数和标准差，求P50.5 X 94 的值； （2）学校对这些被抽取的320名学生进行奖励，奖励方案如下：用频率估计概率，得分小于或等于55的 学生获得1次抽奖机会，得分高于55的学生获得2次抽奖机会.假定每次抽奖抽到价值10元的学习用品的 3 1 概率为 ，抽到价值20元的学习用品的概率为 .从这320名学生中任取一位，记该同学在抽奖活动中获 4 4 得学习用品的价值总额为元，求的分布列和数学期望（用分数表示），并估算此次抽奖要准备的学习 用品的价值总额. 微信搜索“高中试卷君”公众号 领取押题卷联考卷 参考数据：P X 0.6827，P2 X 20.9545， 3 P3 X 30.9973， 210 14.5 ，0.375 8 . 325 【答案】（1） ；（2）分布列见解析， ， 元 0.8186 16 6500 【解析】（1）由折线图可知： 350.025450.15550.2650.25750.225850.1950.0565， 2 356520.025456520.15556520.20 756520.225856520.1956520.05210， 所以14.5，X N  65,14.52 ， 0.9545 0.6827 所以P50.5 X 94P X 2  0.8186. 2 2 （2）由题意可知的可能取值为10，20，30，40， 3 5 则PX 55 ，PX 55 ， 8 8 3 3 9 3 1 5 3 3 57 P10   ，P20      ， 8 4 32 8 4 8 4 4 128 5 1 3 15 5 1 1 5 P30   2 ，P40    ， 8 4 4 64 8 4 4 128 所以的分布列为 10 学科网（北京）股份有限公司 10 20 30 40 9 57 15 5 P 32 128 64 128 9 57 15 5 325 E10 20 30 40  ， 32 128 64 128 16 325 故此次抽奖要准备的学习用品的价值总额约为320 6500元. 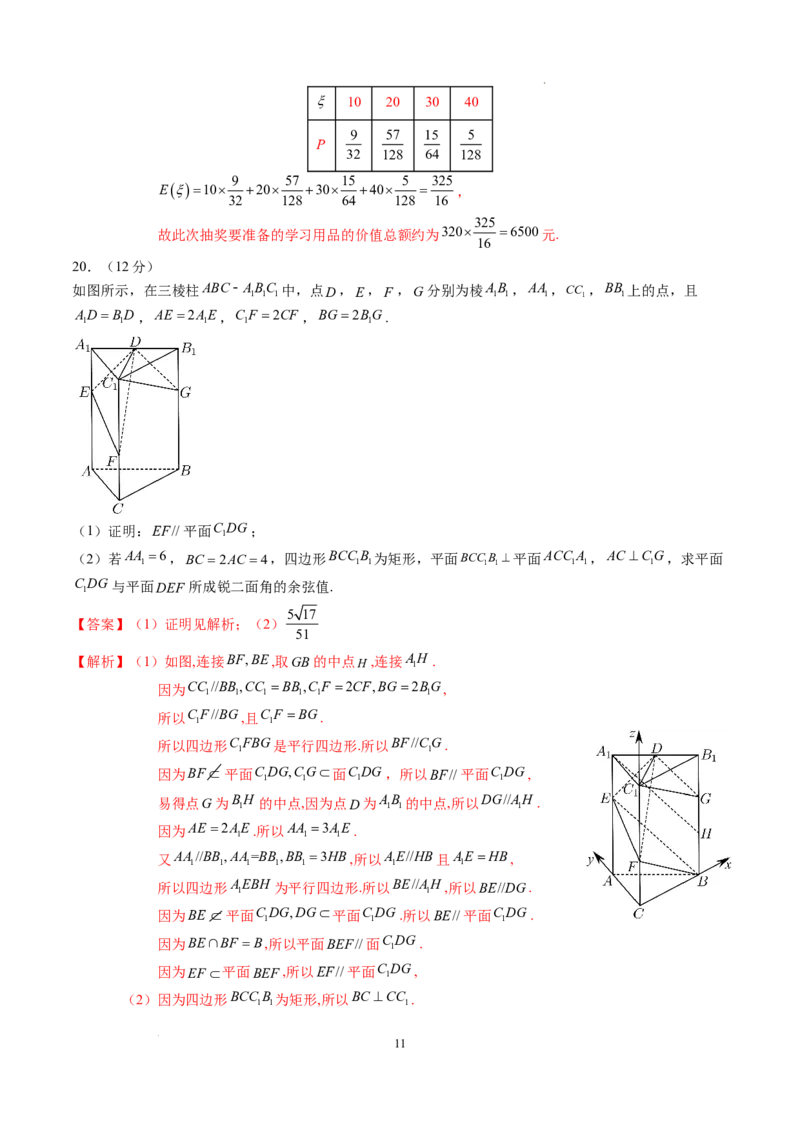16 20．（12分） 如图所示，在三棱柱ABC- A 1 B 1 C 1 中，点D，E，F ，G分别为棱A 1 B 1 ，AA 1 ，CC 1 ，BB 1 上的点，且 ADBD，AE 2AE，CF 2CF ，BG2BG. 1 1 1 1 1 （1）证明：EF//平面CDG； 1 （2）若AA 6，BC 2AC 4，四边形BCCB 为矩形，平面BCCB 平面ACC A ，AC CG，求平面 1 1 1 1 1 1 1 1 C 1 DG与平面DEF 所成锐二面角的余弦值. 5 17 【答案】（1）证明见解析；（2） 51 【解析】（1）如图,连接BF,BE,取GB的中点H ,连接A 1 H . 因为CC //BB,CC BB,CF 2CF,BG2BG, 1 1 1 1 1 1 所以CF//BG,且CF BG. 1 1 所以四边形CFBG是平行四边形.所以BF//CG. 1 1 因为BF 平面CDG,CG面CDG，所以BF//平面CDG, 1 1 1 1 易得点G为B 1 H 的中点,因为点D为A 1 B 1 的中点,所以DG//A 1 H . 因为AE 2AE.所以AA 3AE. 1 1 1 又AA//BB,AA=BB,BB 3HB,所以AE//HB且AEHB, 1 1 1 1 1 1 1 所以四边形AEBH 为平行四边形.所以BE//AH,所以BE//DG. 1 1 因为BE  平面CDG,DG平面CDG.所以BE//平面CDG. 1 1 1 因为BEBF B,所以平面BEF//面CDG. 1 因为EF 平面BEF,所以EF//平面C 1 DG, （2）因为四边形BCCB 为矩形,所以BC CC . 1 1 1 11 学科网（北京）股份有限公司因为平面BCCB 平面ACC A ,平面BCCB 平面ACC A CC ,所以BC平面ACC A ， 1 1 1 1 1 1 1 1 1 1 1 因为AC平面ACC A ,所以BC  AC， 1 1 因为AC CG,所以AC BF. 1 因为BFBC B,BF 平面BCCB ， BC平面BCCB ，所以AC 平面BCCB . 1 1 1 1 1 1 又CC 平面BCCB ,所以AC CC . 1 1 1 1 (cid:6) (cid:6) (cid:6) 以C为原点,CB,CA,CC 1 的方向分别为x轴、y轴、 z 轴的正方向, 建立如图所示的空间直角坐标系， 则C (0,0,6),D(2,1,6),G(4,0,4),E(0,2,4),F(0,0,2), 1 (cid:6) (cid:6) (cid:6) (cid:6) 所以CD(2,1,0),CG(4,0,2),ED(2,1,2),EF (0,2,2)， 1 1 (cid:6) 设平面CDG的法向量为nx,y ,z  , 1 1 1 1 (cid:6) (cid:6)  nCD2x y 0, 则(cid:6)  1 (cid:6) 1 1 令 ,得 . nCG4x 2z 0, x 1 z 2,y 2 1 1 1 1 1 1 (cid:6) 所以平面CDG的一个法向量为n(1,2,2). 1 (cid:6) 设平面DEF 的法向量为mx 2 ,y 2 ,z 2  , (cid:6) (cid:6)  mED2x y 2z 0, 则(cid:6) (cid:6) 2 2 2 令 ,得z 1,x  3 . mEF 2y 2 2z 2 0, y 2 1 2 2 2 (cid:6) 3  所以平面 的一个法向量为m ,1,1. DEF 2  设平面C 1 DG与平面DEF 所成的锐二面角为, 3 (cid:6) (cid:6) 22 (cid:6)(cid:6) |nm| 2 5 17 则cos|cosn,m| (cid:6) (cid:6)   , |n||m| 9 51 144 11 4 5 17 所以平面 与平面 所成锐二面角的余弦值为 . C 1 DG DEF 51 21．（12分） x2 y2 已知点M为双曲线C:  1(a0)右支上除右顶点外的任意点，C的一条渐近线与直线 a2 a22 x 3y20互相垂直． （1）证明：点M到C的两条渐近线的距离之积为定值； 1 （2）已知C的左顶点A和右焦点F，直线 与直线l:x 相交于点N．试问是否存在常数 ，使得 AM 2  AFM AFN？若存在，请求出的值；若不存在，请说明理由． 【答案】（1）证明见解析；（2）存在2，理由见解析 【解析】（1）因为双曲线C的一条渐近线与直线x 3y20互相垂直， a22 所以其中一条渐近线的斜率为 ，则  3，则 ． 3 a a1 12 学科网（北京）股份有限公司y2 所以双曲线C的方程为x2 1． 3 y2 设点M的坐标为x 0 ,y 0 ，则x 0 2 3 0 1，即 3x 0 2y 0 2 3 ． 双曲线的两条渐近线l ，l 的方程分别为 3x y0, 3x y0， 1 2 3x  y 3x  y 则点M到两条渐近线的距离分别为d  0 0 ,d  0 0 ， 1 2 2 2 则dd  3x 0  y 0  3x 0  y 0  3x 0 2 y 0 2  3 ． 1 2 2 2 4 4 所以点M到双曲线C的两条渐近线的距离之积为定值． （2）存在2． ①当x  2时， MF  AF 3，又N是AM 的中点， 0 所以AFN MFN 45，所以AFM 2AFN ，此时2． ②当x 2时． 0 y k  0 ⅰ）当M在x轴上方时，由 A1,0,Mx ,y ，可得 AM x 1 ， 0 0 0 y 所以直线 的直线方程为y 0 x1 ， x 1 AM 0 1 3y  把x 1 代入得N 2 , 2x  0 1   ． 2  0  3 y  0 2 x 1 y 所以k  0  0 ，则 y ． NF 1 x 1 tanAFN  0 2 0 x 1 2 0 y 2 0 x 1 2x 1y y tan2AFN  0  0 0  0 由二倍角公式可得  y  2 x 12  y2 2x ． 1 0  0 0 0 x 1 0 y 因为直线 的斜率k  0 及 ， MF x 2 tanAFM k MF 0 MF y 所以tanAFM  0 ，则 ． 2x tanAFM tan2AFN 0  π 因为AFM0,π,AFN0, ，所以 ．  2 AFM 2AFN ⅱ）当M在x轴下方时，同理可得AFM 2AFN ． 故存在2，使得AFM 2AFN ． 22．（12分）微信搜索“高中试卷君”公众号 领取押题卷联考卷 已知函数 f xln1x ，gxax2x. （1）当x1时， f x gx ，求实数a的取值范围； 13 学科网（北京）股份有限公司1 1 1 （2）已知 ，证明：sin sin sin ln2. nN* n1 n2 2n 【答案】（1）a0；（2）证明见解析 1 x 【解析】（1）令hxlnx1xx1，则hx 1 ， x1 x1 当1x0时，hx0，则函数hx 在 1,0 上单调递增， 当x0时，hx0，则函数hx 在 0, 上单调递减， 所以，hx h00，即lnx1x， max 所以，当a0时，lnx1xax2x，即 f x gx ， 1 当 时，取x  0， a<0 0 a  1 2 1 由于 ln1x 0 ln10 ，而ax 0 2x 0 a   a    a 0，得 lnx 0 1ax 0 2x 0 ， 故 f x gx  ，不合乎题意. 0 0 综上所述，a0. （2）证明：当a0时，由（1）可得lnx1x，则lnxx1， 可得ln 1  1 1，即lnx 1 1，即lnx1 1 x1 ， x x x x 1 1 t t 1 1 令 1 ，所以，x ，所以，ln  ，即lntlnt1 t1 ， t x t1 t1 t t 1 所以， nk lnnklnnk1 ，k0,1,2,,n， 令gxxsinxx0 ，则gx1cosx0，且gx 不恒为零， 所以，函数gx 在 0, 上单调递增，故gxg00，则sinxxx0， 1 1 所以，sin nk  nk lnnklnnk1 ，k0,1,2,,n， 1 1 1 所以，sin sin sin n1 n2 2n 2n   lnn1lnn    lnn2lnn1    ln2nln2n1  ln2nlnnln n 2. 14 学科网（北京）股份有限公司15 学科网（北京）股份有限公司