越秀区广州华侨外国语学校2024-2025学年九年级数学_广州九上月考+期中+期末+一模二模+中考真题_九上月考_初三上十月考

2024 学年第一学期九年级适应性调研 数学问卷 （时间：90分钟，分值：120分） 一、选择题（31030分） 1. 方程x(x-6)=0的解是（ ） A. x=6 B. x =0，x =6 C. x=-6 D. x =0，x =-6 1 2 1 2 x x2 3xm0 2. 已知关于 的方程 的一个根是2，则此方程的另一根为（ ） A. 0 B. 1 C. 2 D. 3 3. 每年春秋季节流感盛行，极具传染性如果一人得流感，不加干预，则经过两轮后共有81人得流感，则 x 每人每轮平均会感染几人？设每人每轮平均感染 人，则下列方程正确的是（ ） 1xx2 81 x12 81 A. B. 1xx12 81 1x11x2 81 C. D. m x2 6x20 2m2 12m 4. 已知 是方程 的一个根，则 的值为（ ） A. 4 B. 4 C. 2 D. 2 y 5x2 5. 若将抛物线 先向右平移2个单位，再向上平移1个单位，得到的新抛物线的表达式为（ ） y 5x22 1 y 5x22 1 A B. . y 5x22 1 y 5x22 1 C. D. x x2 4xk 0 k 6. 关于 的一元二次方程 有两个实数根，则 的取值范围是（ ） A. k 4 B. k 4 C. k 4 D. k 4 7. 已知x 、x 、是一元二次方程x2+x-2=0的两个根，则x +x +x x 的值为（ ） 1 2 1 2 1 2 A. 1 B. -3 C. 3 D. -2 y x22 2 的 8. 抛物线 与y轴 交点坐标是（ ） 2，2 0，6 0，2 0，4 A. B. C. D. y ax2 bx y bxa 9. 抛物线 和直线 在同一坐标系内的图像如图，其中正确的是（ ） 第1页/共4页 学科网（北京）股份有限公司A. B. C. D. Pm,n Q3,0 y kxb k 0 10. 已知点 ， 都在一次函数 （k，b是常数， ）图象上，（ ） mn 9 mn 9 A. 若 有最大值4，则k的值为 B. 若 有最小值4，则k的值为 mn 9 mn 9 C. 若 有最大值 ，则k的值为4 D. 若 有最小值 ，则k的值为4 二、填空题（3618分） y  x2 4x5的 11. 抛物线 顶点坐标是________． y (x2)2 12. 把二次函数 的图像沿y轴向上平移1个单位长度，与y轴的交点为C，则C点坐标是 ． 13. 某药品原价是100元，经连续两次降价后，价格变为64元，如果每次降价的百分率是一样的，那么每 次降价的百分率是_______ A1,y ,B1,y ,C4,y  y x32 k y ,y ,y 14. 已知 1 2 3 三点都在二次函数 的图象上，则 1 2 3的大小 关系为___________ kx2 2x10 15. 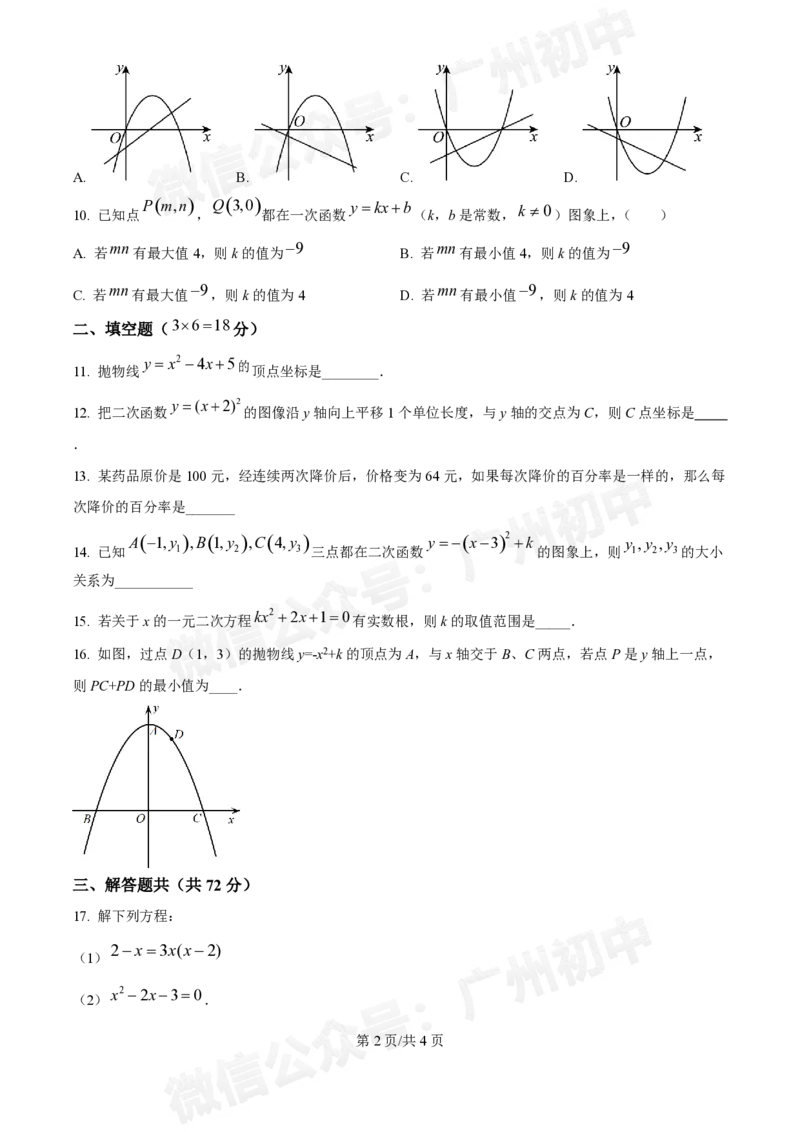若关于x的一元二次方程 有实数根，则k的取值范围是_____． 16. 如图，过点D（1，3）的抛物线y=-x2+k的顶点为A，与x轴交于B、C两点，若点P是y轴上一点， 则PC+PD的最小值为____． 三、解答题共（共72分） 17. 解下列方程： 2x 3x(x2) （1） x2 2x30 （2） ． 第2页/共4页 学科网（北京）股份有限公司18. 已知关于x的方程：x2﹣（6+m）x+9+3m＝0． （1）求证：无论m为何值，方程都有实数根． （2）若该方程的两个实数根恰为斜边为5的直角三角形的两直角边长，求m的值． y ax2 bxc 19. 抛物线 上部分点的横坐标x，纵坐标y，的对应值如下表： 2 x … 1 0 1 2 … 4 4 y … 0 0 8 … （1）根据上表填空： ①抛物线经过点（3，__________），对称轴为__________； y0 ②当 时，x取值范围是 __________； y ax2 bxc （2）求该抛物线 的解析式． 20. 第二十届省运会将于2022年在泰州举行，运动会纪念徽章在网上进行销售．平均每天可售出100枚， 每枚售价20元．为了扩大销售，现采取了降价措施，在每枚售价不少于15元的前提下，销售一段时间后， a 发现销售单价每降低1元，平均每天可多售出10枚，若每枚商品降价 元． a a （1）降价后平均每天销售数量为 枚（用含 的代数式表示）， 的取值范围是 ； a （2）若该网店每天销售额为2160元时，求 的值． 的 x2 (2m1)xm2 20 21. 已知关于x 一元二次方程 ． （1）若该方程有两个实数根，求m的最小整数值； x ,x x x 2 m2 21 （2）若方程的两个实数根为 1 2，且 1 2 ，求m的值． ABCD 22. 园林部门计划在某公园建一个长方形苗圃 ，苗圃的一面靠墙（墙最大可用长度为14米）．另三 边用木栏围成，中间也用垂直于墙的木栏隔开，分成两个区域，并在如图所示的两处各留2米宽的门（门 ABCD CD 不用木栏），建成后所用木栏总长32米，设苗圃 的一边 长为x米． 第3页/共4页 学科网（北京）股份有限公司ABCD 96m2 （1）若苗圃 的面积为 ，求x的值； ABCD （2）当x为何值时，苗圃 的面积最大，最大面积为多少？ y (xm)(xm2) m0 23. 在平面直角坐标系中，设二函数 1 ，其中 ． y （1）求证：函数 1与x轴有交点； y mxn y （2）若函数 2 经过函数 1的顶点，求实数n的最大值； P(3,a),Qx ,b y ab x （3）已知点 1 在函数 1的图象上，若 ，求 1的取值范围． 第4页/共4页 学科网（北京）股份有限公司