越秀区第十六中学2024-2025学年九年级数学10月月考试题（答案解析）_广州九上月考+期中+期末+一模二模+中考真题_九上月考_初三上十月考

2024 学年第一学期十六中教育集团阶段教学质量反馈 九年级数学（问卷） 一、选择题（每小题3分，共30分） 1. 下列图标中，既是轴对称图形，又是中心对称图形的是（ ） A. B. C. D. 【答案】D 【解析】 【分析】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折 180 叠后可重合，中心对称图形是要寻找对称中心，旋转 后与原图重合．根据轴对称图形和中心对称图形 的概念对各选项分析判断即可得解． 【详解】解：A．是轴对称图形，不是中心对称图形，故本选项不合题意； B、既不是轴对称图形，也不是中心对称图形，故本选项不合题意； C、是轴对称图形，不是中心对称图形，故本选项不符合题意； D、是轴对称图形，也是中心对称图形，故本选项符合题意． 故选∶D． y 2(x1)2 6 2. 抛物线 的顶点坐标为（ ） (1,6) (1,6) (1,6) (1,6) A. B. C. D. 【答案】B 【解析】 【分析】本题考查二次函数的性质，根据抛物线的顶点式，可以直接写出顶点坐标． y 2(x1)2 6 【详解】解：∵抛物线 ， 第1页/共23页 学科网（北京）股份有限公司(1,6) ∴该抛物线的顶点坐标为 ， 故选：B． x2 x10 3. 一元二次方程 的根的情况是（ ） A. 没有实数根 B. 有两个相等的实数根 C. 有两个不相等的实数根 D. 有一个实数根 【答案】A 【解析】 【分析】根据一元二次方程根的判别式进行计算即可求解． x2 x10 a1,b1,c1 【详解】解：∵一元二次方程 中， b2 4ac1430 ∴ ， 该方程没有实数根， 故选A． ax2 bxc0 a 0，a，，b c b2 4ac 【点睛】本题考查了一元二次方程 ( 为常数)的根的判别式 ，  0 理解根的判别式对应的根的三种情况是解题的关键．当 时，方程有两个不相等的实数根；当  0 0 时，方程有两个相等的实数根；当 时，方程没有实数根． x2 2x50 4. 用配方法解方程 时，原方程应变形为（ ） x12 6 x12 6 x22 9 x22 9 A. B. C. D. 【答案】B 【解析】 【分析】本题主要考查了配方法解一元二次方程，先把常数项移到方程右边，再把方程两边同时加上一次 项系数一半的平方进行配方即可得到答案． x2 2x50 【详解】解： ， x2 2x5 ， x2 2x16 ， x12 6 ， 故选：B． 5. 某同学在用描点法画二次函数的图象时，列出了下面的表格： 第2页/共23页 学科网（北京）股份有限公司2 x …… 1 0 1 2 3 …… 3 4 3 y …… 5 0 m …… 那么m的值为（ ） A. 3 B. 4 C. 0 D. 5 【答案】C 【解析】 【分析】本题考查了二次函数的图象的性质．根据题目提供的满足二次函数解析式的x、y的值，确定二次 函数的对称轴，利用对称轴找到一个点的对称点的纵坐标即可． 0，3 2，3 【详解】解：由上表可知函数图象经过点 和点 ， 02 x 1 ∴对称轴为 2 ， ∴当x1时的函数值等于当 x3 时的函数值， ∵当x1时， y0 ， ∴当 x3 时，m0． 故选：C． y 5x2 的 6. 把抛物线 向左平移2个单位，再向上平移3个单位，得到 抛物线是（ ） y5x22 3 y5x22 3 y5x22 3 y5x22 3 A. B. C. D. 【答案】C 【解析】 【分析】按照“左加右减，上加下减”的规律进行解答即可． y 5x2 y5x22 3 【详解】把抛物线 向左平移2个单位，再向上平移3个单位，得到的抛物线是 故选C． 【点睛】本题考查了抛物线的平移及抛物线解析式的变化规律：左加右减、上加下减． 7. 若  ，  是方程x2 2x10的两根，则  的值为（ ） A. 1 B. -1 C. 3 D. -3 第3页/共23页 学科网（北京）股份有限公司【答案】A 【解析】 2,1 【详解】根据韦达定理，得： ，  则 =2-1=1. 故选：A. 8. 有两个直角三角形纸板，一个含45°角，另一个含30°角，如图①所示叠放，先将含30°角的纸板固 定不动，再将含45°角的纸板绕顶点A顺时针旋转，使BC∥DE，如图②所示，则旋转角∠BAD的度数 为（ ） A. 15° B. 30° C. 45° D. 60° 【答案】B 【解析】 【分析】由平行线的性质可得∠CFA＝∠D＝90°，由外角的性质可求∠BAD的度数． 【详解】解：如图，设AD与BC交于点F， ∵BC∥DE， ∴∠CFA＝∠D＝90°， ∵∠CFA＝∠B+∠BAD＝60°+∠BAD， ∴∠BAD＝30° 故选：B． 【点睛】本题考查了平行线的性质以及外角的性质，熟知以上知识点是解题的关键． 第4页/共23页 学科网（北京）股份有限公司9. 如图，幼儿园计划用30m的围栏靠墙围成一个面积为100m2的矩形小花园（墙长为15m），则与墙垂直 的边x为（ ） A. 10m或5m B. 5m或8m C. 10m D. 5m 【答案】C 【解析】 【分析】设与墙垂直的边长x米，则与墙平行的边长为（30﹣2x）米，根据矩形的面积公式结合矩形小花 园的面积为100m2，即可得出关于x的一元二次方程，解之取其较大值即可得出结论． 【详解】设与墙垂直的边长x米，则与墙平行的边长为（30﹣2x）米， 根据题意得：（30﹣2x）x＝100， 整理得：x2﹣15x+50＝0， 解得：x ＝5，x ＝10． 1 2 当x＝5时，30﹣2x＝20＞15， ∴x＝5舍去． 故选C． 【点睛】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键． △BCD BC 10. 如图，BD为矩形ABCD的对角线，将△BCD沿BD翻折得到 ， 与边AD交于点E．若 AB＝x ，BC＝2x ，DE＝3，其中x 、x 是关于x的方程x2﹣4x+m＝0的两个实根，则m的值是（ 1 2 1 2 ） 16 12 5 5 A. B. C. 3 D. 2 【答案】A 【解析】 1 1 的 2 2 【分析】利用根与系数 关系得到x ＋x ＝4，x x ＝m，AB＋ BC＝4，m＝AB× BC，再利用折叠的 1 2 1 2 第5页/共23页 学科网（北京）股份有限公司性质和平行线的性质得到∠EBD＝∠EDB，则EB＝ED＝3，所以AE＝AD−DE＝5−2AB，利用勾股定理得 102 5 102 5 204 5 到AB2＋（5−2AB）2＝32，解得AB＝ 5 或AB＝ 5 （舍去），则BC＝ 5 ，然后计 算m的值． 【详解】∵x 、x 是关于x的方程x2−4x＋m＝0的两个实根， 1 2 ∴x ＋x ＝4，x x ＝m， 1 2 1 2 1 1 2 2 即AB＋ BC＝4，m＝AB× BC， ∵△BCD沿BD翻折得到△BC′D，BC′与边AD交于点E， ∴∠CBD＝∠EBD， ∵AD∥BC， ∴∠CBD＝∠EDB， ∴∠EBD＝∠EDB， ∴EB＝ED＝3， 在Rt△ABE中，AE＝AD−DE＝BC−3＝8−2AB−3＝5−2AB， 102 5 102 5 ∴AB2＋（5−2AB）2＝32，解得AB＝ 5 或AB＝ 5 （舍去）， 204 5 ∴BC＝8−2AB＝ 5 ， 1 102 5 204 5 16 ∴m＝ 2 × 5 × 5 ＝ 5 ． 故选：A． 的 【点睛】本题考查了根与系数 关系：若x ，x 是一元二次方程ax2＋bx＋c＝0（a≠0）的两根时， 1 2 b c a a x ＋x ＝− ，x x ＝ ．也考查了矩形的性质和折叠的性质． 1 2 1 2 二、填空题（每小题3分，共18分） x2 y  11. 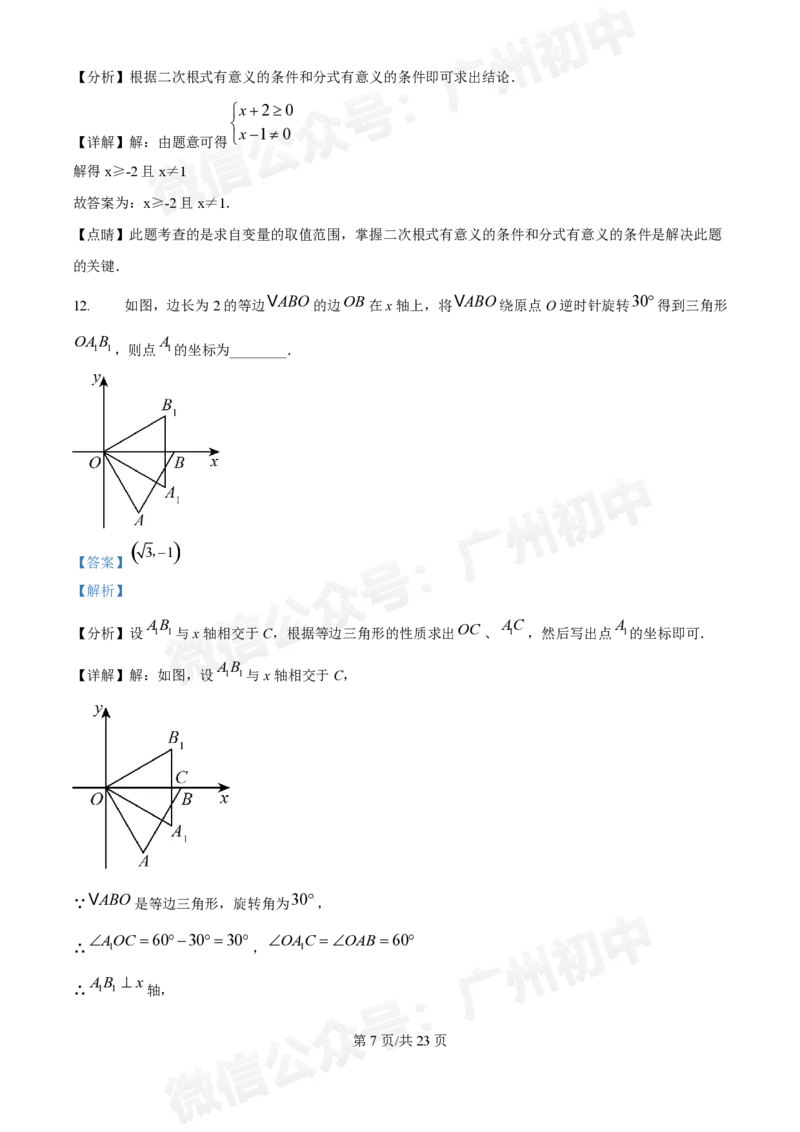函数 x1 中，自变量x的取值范围是__________． 【答案】x≥-2且x≠1 【解析】 第6页/共23页 学科网（北京）股份有限公司【分析】根据二次根式有意义的条件和分式有意义的条件即可求出结论． x20  x10 【详解】解：由题意可得 解得x≥-2且x≠1 故答案为：x≥-2且x≠1． 【点睛】此题考查的是求自变量的取值范围，掌握二次根式有意义的条件和分式有意义的条件是解决此题 的关键． VABO OB VABO 30 12. 如图，边长为2的等边 的边 在x轴上，将 绕原点O逆时针旋转 得到三角形 OAB A 1 1，则点 1的坐标为________．   3，1 【答案】 【解析】 AB AC A 【分析】设 1 1与x轴相交于C，根据等边三角形的性质求出OC、 1 ，然后写出点 1的坐标即可． AB 【详解】解：如图，设 1 1与x轴相交于C， VABO 30 ∵ 是等边三角形，旋转角为 ， AOC 603030 OAC OAB 60 ∴ 1 ， 1 AB  x ∴ 1 1 轴， 第7页/共23页 学科网（北京）股份有限公司VABO ∵等边 的边长为2， OA OA2 ∴ 1 ， AOC 30 ∵ 1 ， AC 1 OC  OA2 AC2  3 ∴ 1 ， 1 1 ， A 又∵ 1在第四象限，   A 3，1 ∴点 1的坐标为   3，1 故答案为： ． 【点睛】本题考查了坐标与图形变化−旋转，直角三角形的性质，等边三角形的性质，熟记等边三角形的 性质是解题的关键． 13. 若y=（a-1）x3a2−1是关于x的二次函数，则a=________ 【答案】-1 【解析】 【详解】由二次函数的定义可知自变量的最高指数为2，且系数不等于0，可得3a2-1=2；解得a=±1；又 因a-1≠0；即a≠1；最终可求得a=-1． 故答案为-1. 点睛：此题主要考查了二次函数的概念，由二次函数的定义可知自变量的最高指数为2，且系数不等于 0，列出方程与不等式解答是关键. 14. 抛物线 y 2x2 bx3 的对称轴是直线 x1 ，则b的值为___． 【答案】4 【解析】 【分析】根据抛物线的对称轴公式即可求解． Q y2x2 bx3 x1 【详解】解： ，对称轴是直线 ， b b  1  1  2a ，即 4 ，解得 b4 ． 故答案为：4． b x 【点睛】本题考查了二次函数的性质，掌握抛物线y＝ax2＋bx＋c（a≠0）的对称轴是直线 2a 是解 题的关键． 第8页/共23页 学科网（北京）股份有限公司x2 x10 20262a2 2a 15. 若a是方程 的一个根，则代数式 的值是__________． 2024 【答案】 【解析】 【分析】本题考查一元二次方程的解：能使一元二次方程左右两边相等的未知数的值称为一元二次方程的 20262a2 2a 20262  a2 a  a2 a 1 解．由题意得 ，根据 ，利用整体思想即可求解． a2 a10 【详解】解：由题意得： ， a2 a 1 ∴ ， 20262a2 2a 20262  a2 a  2026212024 ∴ ． 2024 故答案为： ． y ax2 bxca0 3,0 x  2 16. 如图，抛物线 的对称轴为直线 ，抛物线与x轴的一个交点在 和 4,0 之间，其部分图象如图所示．有下列结论： 4ab0 c0 3ac0 ① ；② ；③ ；  9   5   1   ,y  ,y  ,y        2 1   2 2   2 3  y  y  y ④若 ， ， 是该抛物线上的三点，则 1 2 3； 4a2bat2 bt ⑤ （t为实数）． 其中正确结论的序号有__________． 【答案】①③⑤ 【解析】 【分析】此题主要考查了二次函数的图象与系数之间的关系，解答此题的关键是熟练掌握二次函数图象的 开口方向、顶点坐标、对称轴、与坐标轴的交点坐标． x 根据抛物线的对称轴可对结论①进行判断；根据抛物线与 轴的两个交点坐标的位置可判断出抛物线与 第9页/共23页 学科网（北京）股份有限公司y x 轴交点的位置，进而可对结论②进行判断；根据抛物线与 轴的两个交点坐标的位置可判断出点 (1,abc) x  2 的位置，进而可对结论③进行判断；根据抛物线的开口向下，且对称轴为直线 可知： 在抛物线上离对称轴水平距离越小，函数的值就越大，据此可对结论④进行判定；根据抛物线的对称轴可 (2,4a2bc) y 4a2bc 求出顶点坐标为 ，由此可判定 为抛物线的最大值，据此可对结论⑤进行判 断，进而可得出答案． 【详解】解：① Q抛物线的对称轴为直线 x  2 ， b  2  2a ， 4ab0，故结论①正确； ② Q抛物线的开口向下，与 x 轴的一个交点在 (3,0) 和 (4,0) 之间， 抛物线与 x 轴的另一个交点在 (1,0) 和 (0,0) 之间， y 抛物线与 轴的交点在负半轴上， c0 ，故结论②错误； ③对于 y ax2 bxc ，当x1时， y abc ， Q抛物线与 x 轴的另一个交点在 (1,0) 和 (0,0) 之间，开口向下， (1,abc) 点 在第二象限， abc0 ， 4ab0 由① ， b4a ， a4ac0 3ac0 ，即： ，故结论③正确； ④ Q抛物线的开口向下，且对称轴为直线 x  2 ， 观察函数的图象可知：在抛物线上离对称轴水平距离越小，函数的值就越大， y  y  y 2 3 1，故结论④不正确． y ax2 bxc x  2 y 4a2bc xt(t y at2 btc ⑤对于 ，当 时， ，当 为实数）时， ， Q抛物线的对称轴为直线 x  2 ， 第10页/共23页 学科网（北京）股份有限公司点 (2,4a2bc) 为抛物线的顶点， 又Q抛物线的开口向下， y 4a2bc 为抛物线的最大值， 4a2bcat2 btc，即： 4a2bat2 bt ，故结论⑤正确； 综上所述：正确的结论是①③⑤． 故答案为：①③⑤． 三、解答题（本大题共9题，共72分） x2 4x30 17. 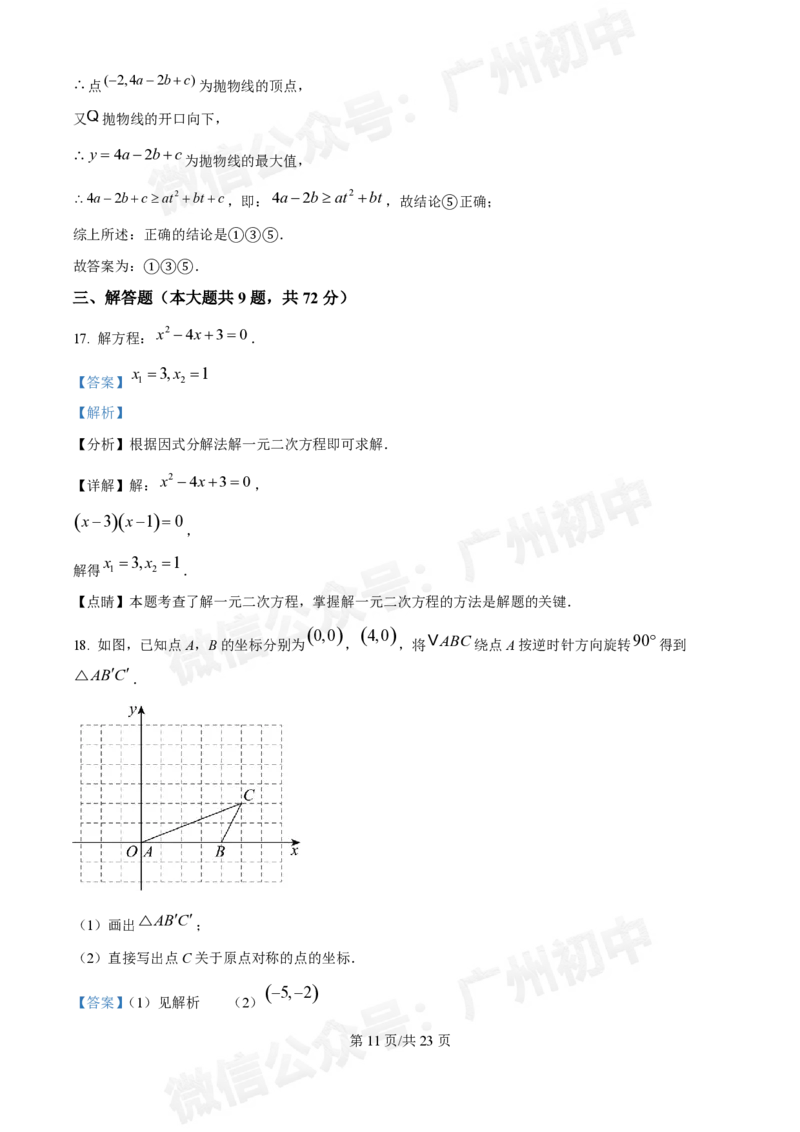解方程： ． x 3,x 1 【答案】 1 2 【解析】 【分析】根据因式分解法解一元二次方程即可求解． x2 4x30 【详解】解： ， x3x10 ， x 3,x 1 解得 1 2 ． 【点睛】本题考查了解一元二次方程，掌握解一元二次方程的方法是解题的关键． 0,0 4,0 18. 如图，已知点A，B的坐标分别为 ， ，将 VABC绕点A按逆时针方向旋转 90 得到 △ABC ． （1）画出△ABC ； （2）直接写出点C关于原点对称的点的坐标． 5,2 【答案】（1）见解析 （2） 第11页/共23页 学科网（北京）股份有限公司【解析】 【分析】本题主要考查了旋转作图、关于原点中心对称的性质，根据题意画出旋转后的图形是解题的关 键． （1）将点C，B的坐标分别绕点A按逆时针方向旋转 90 得到对应点 C ，B，顺次连接各点即可得到 △ABC ； （2）根据关于原点对称的点的坐标特点求解即可． 【小问1详解】 解：如图所示，△ABC 即为所求； 【小问2详解】 C5,2 解：∵ ， 5,2 ∴点C关于原点对称的点的坐标为 ． 19. 某市为减少汽车尾气污染，改善空气质量，鼓励市民选择新能源汽车作为出行的交通工具，并大力推 进新能源汽车充电基础设施建设．据统计，该市2020年新建100座充电站，2022年新建169座，求该市 这两年新建充电站的数量的年平均增长率． 30% 【答案】 【解析】 【分析】本题考查了一元二次方程的应用，解题的关键是：找准等量关系，正确列出一元二次方程，难度 不大． x 设该市这两年新建充电站的数量的年平均增长率为 ，，根据该市2020年底和2022年底的充电站数，即 x 可得出关于 的一元二次方程，解之取其正值即可得出结论． x 【详解】解：设新建充电站的数量的年平均增长率为 ， 100(1x)2 169 根据题意得： ． 第12页/共23页 学科网（北京）股份有限公司x 0.330% x 2.3 解得： 1 ， 2 （舍去）． 30% 答：该市这两年新建充电站的数量的年平均增长率为 ． y ax2 bxca 0 20. 已知二次函数 ，函数y与自变量x的部分对应值如下表： 2 x …… 1 0 1 2 …… 3 4 3 y …… 5 0 …… （1）求该二次函数的表达式； y ax2 bxc ax2 bxc0 （2）根据二次函数 图象，直接写出不等式 的x的取值范围． y=x22x3 【答案】（1） x3 x1 （2） 或 【解析】 【分析】本题考查了二次函数与不等式（组），待定系数法求函数解析式，关键是求出函数的解析式． （1）利用待定系数法确定函数关系式； x （2）根据函数的图象，求 的取值范围即可． 【小问1详解】 1,4 解：由表格可知抛物线的顶点坐标为 ． y ax12 4 设抛物线的解析式为 ， 1,0 Q抛物线过点 ， 0a112 4 ， a1， y x12 4 x2 2x3 ∴ y=x22x3 二次函数的表达式为 ； 【小问2详解】 解：Q抛物线开口向上，对称轴为直线 x1 ， 第13页/共23页 学科网（北京）股份有限公司1,0 3,0 点 的对称点为 ， 不等式 ax2 bxc0 的 x 的取值范围是 x3 或 x1 ． 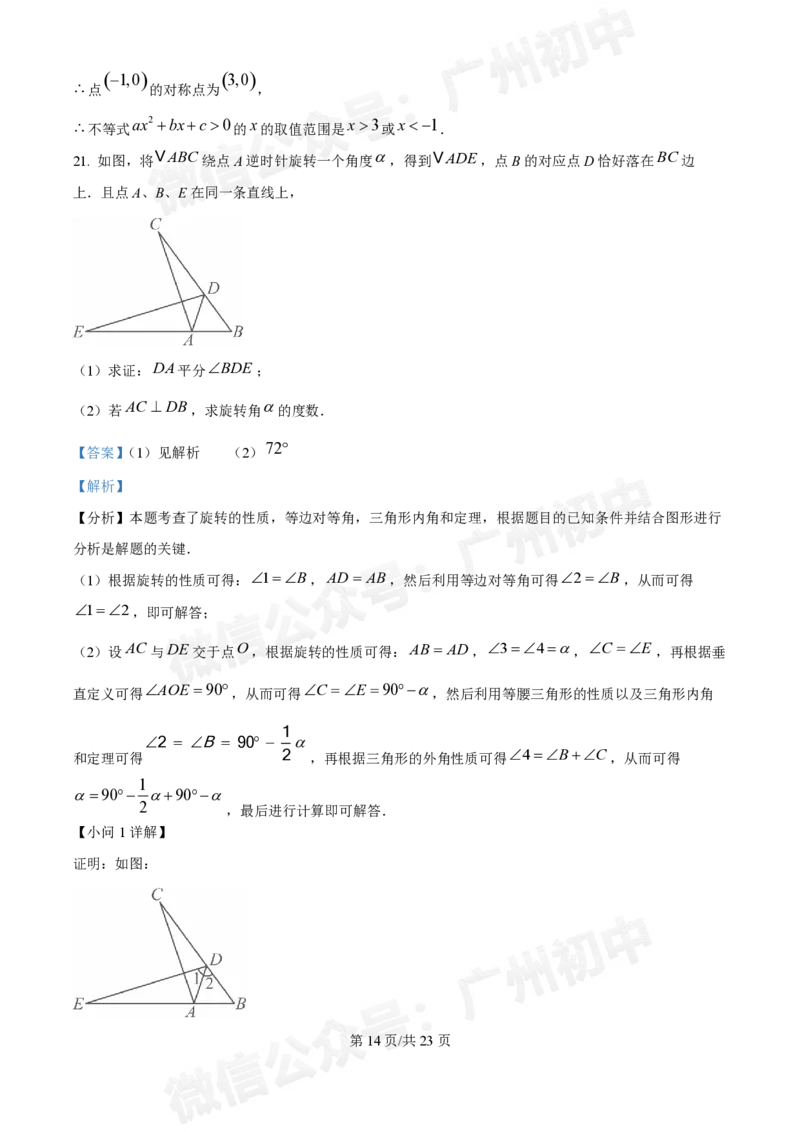21. 如图，将 VABC绕点A逆时针旋转一个角度  ，得到VADE，点B的对应点D恰好落在BC边 上．且点A、B、E在同一条直线上， （1）求证：DA平分BDE； AC  DB  （2）若 ，求旋转角 的度数． 72 【答案】（1）见解析 （2） 【解析】 【分析】本题考查了旋转的性质，等边对等角，三角形内角和定理，根据题目的已知条件并结合图形进行 分析是解题的关键． （1）根据旋转的性质可得：1B，AD AB，然后利用等边对等角可得2B，从而可得 12，即可解答； （2）设 AC 与DE交于点 O ，根据旋转的性质可得：AB AD，34， C E ，再根据垂 AOE 90 C E 90 直定义可得 ，从而可得 ，然后利用等腰三角形的性质以及三角形内角 1 2  B 90   和定理可得 2 ，再根据三角形的外角性质可得4BC，从而可得 1 90 90 2 ，最后进行计算即可解答． 【小问1详解】 证明：如图： 第14页/共23页 学科网（北京）股份有限公司由旋转得：1B，AD AB， 2B， 12， DA平分EDB； 【小问2详解】 解：如图，设 AC 与DE交于点 O ， 由旋转得：AB AD，34， C E ， QAC  DE ， AOE 90， C E 90490 ， Q AB AD， 1803 180 1 2B  90  2 2 2 ， Q4是 VABC的一个外角， 4BC ， 1 90 90 2 ， 72 解得： ， 旋转角  的度数为 72 ． x2 2k1xk2 k 0 22. 已知关于x的一元二次方程 （1）求证：方程有两个不相等的实数根； （2）若△ABC的两边AB、AC的长是方程的两个实数根，第三边BC的长为5．当△ABC是等腰三角形时， 求k的值 【答案】（1）详见解析 （2）k 4或k 5 第15页/共23页 学科网（北京）股份有限公司【解析】 【分析】（1）先计算出△=1，然后根据判别式的意义即可得到结论； （2）先利用公式法求出方程的解为x =k，x =k+1，然后分类讨论：AB=k，AC=k+1，当AB=BC或AC=BC 1 2 时△ABC为等腰三角形，然后求出k的值． 【详解】（1）证明：∵△=（2k+1）2-4（k2+k）=1＞0， ∴方程有两个不相等的实数根； 2k1 1 （2）解：一元二次方程x2-（2k+1）x+k2+k=0的解为x= 2 ， 即x =k，x =k+1， 1 2 ∵k＜k+1， ∴AB≠AC． 当AB=k，AC=k+1，且AB=BC时，△ABC是等腰三角形，则k=5； 当AB=k，AC=k+1，且AC=BC时，△ABC是等腰三角形，则k+1=5，解得k=4， 所以k的值为5或4． 【点睛】本题考查了：1．根的判别式；2．解一元二次方程；3．三角形三边关系；4．等腰三角形的性 质． 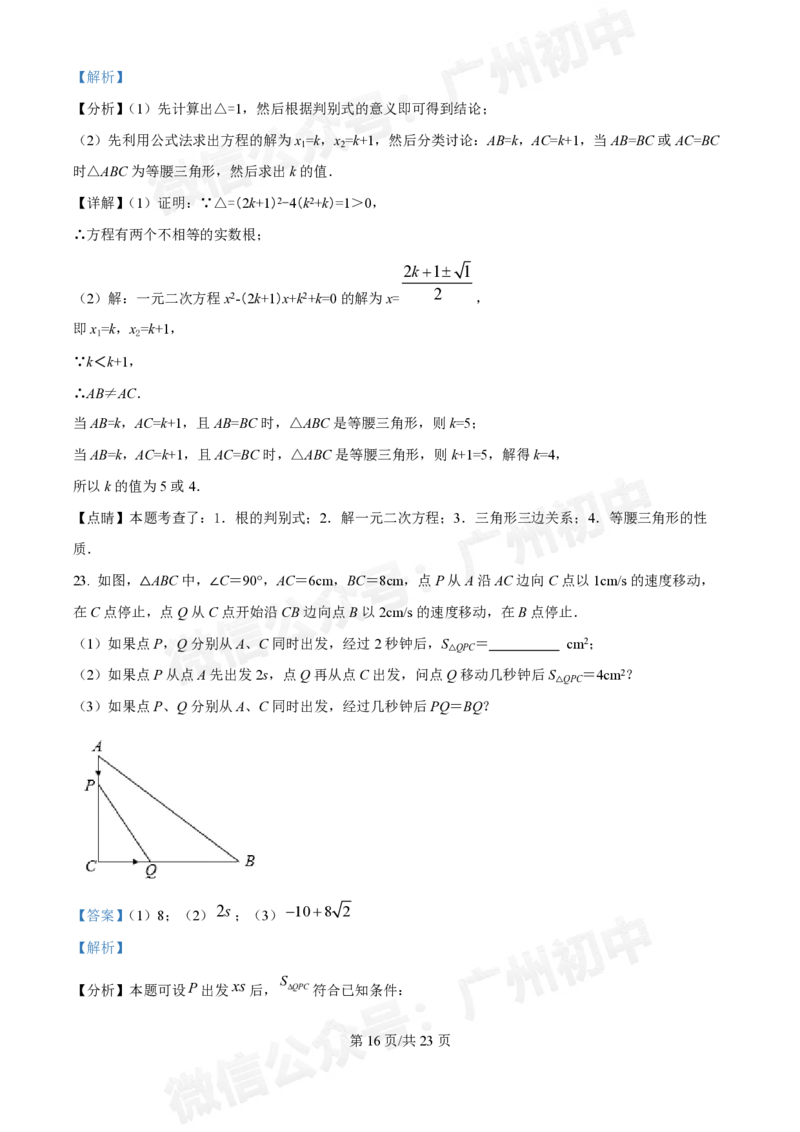23. 如图，△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P从A沿AC边向C点以1cm/s的速度移动， 在C点停止，点Q从C点开始沿CB边向点B以2cm/s的速度移动，在B点停止． （1）如果点P，Q分别从A、C同时出发，经过2秒钟后，S ＝ cm2； △QPC （2）如果点P从点A先出发2s，点Q再从点C出发，问点Q移动几秒钟后S ＝4cm2？ △QPC （3）如果点P、Q分别从A、C同时出发，经过几秒钟后PQ＝BQ？ 【答案】（1）8；（2） 2s ；（3）108 2 【解析】 【分析】本题可设P出发 xs 后， S QPC符合已知条件： 第16页/共23页 学科网（北京）股份有限公司1 S  (6x)g2x 在（1）中， AP xm ， PC (6x)m ， QC 2xm ，得出 QPC 2 ，即可求出经过2秒钟后的 面积； AP xm PC (6x)m QC 2(x2)m 在（2）中， ， ， ，进而可列出方程，求出答案； PC (6x)m QC 2xm BQ82x PQ BQ 在（3）中， ， ， ，利用勾股定理和 列出方程，求出答 案． 1 S  (6x)g2x 【详解】解：（1）P、 Q 同时出发，经过 x 秒钟， QPC 2 ， x2 当 ， 1 1 S  (6x)g2x 448 QPC 2 2 ， 故答案是：8． （2）设P出发 ts 时 S QPC 4cm2 ，则 Q 运动的时间为 (x2) 秒，由题意得： 1 (6x)g2(x2)4 2 ， x2 8x160， x  x 4 解得： 1 2 因此经4秒点P离A点 144cm ，点 Q 离C点 2(42)4cm ，符合题意． 答：P先出发 2s ， Q 再从C出发 2s 后， S QPC 4cm2 ． x PQ BQ PC (6x)m QC 2xm BQ82x （3）设经过 秒钟后 ，则 ， ， ， (6x)2 (2x)2 (82x)2 ， x 108 2 x 108 2 解得 1 ， 2 （不合题意，舍去） 答：经过108 2 秒钟后 PQ BQ ． 【点睛】本题考查一元二次方程的实际运用，解题的关键是弄清图形与实际问题的关系，另外，还要注意 解的合理性，从而确定取舍． x x2 2bxc0 24. 已知关于 的方程 有两个相等的实数根． b1 c （1）若 ，求 的值；  1 1 B b , b0 （2）在 VABC中，已知点 A0,c ，点   b c   ，点C在 x 轴上，且该方程的解是点C的横 第17页/共23页 学科网（北京）股份有限公司坐标． ①过点C作CDx轴，交边AB于点D，求证： CD 的长为定值； ②求 VABC面积的最小值． 【答案】（1）1 （2）①1；②1 【解析】 【分析】（1）利用根的判别式计算即可． （2）①根据方程确定点C的横坐标，判定点C的位置，统一字母表示，确定直线AB的解析式，再确定 CD 点D的坐标，计算 的长即可． 2  1  1 1 1 b  0 b0, 0   b 2 S = CD´ B ②根据 b 得到  b  即 b ，结合 VABC 2 x ，计算即可． 【小问1详解】 x x2 2bxc0 ∵关于 的方程 有两个相等的实数根， 2b2 4c0 ∴ ， b2 c ∴ ， b1 当 时， cb2 1 ． 【小问2详解】 x x2 2bxc0 ①∵关于 的方程 有两个相等的实数根， b 2b x  b ∴ 2a 2 ， Cb,0 点 ，  1 1 B b , b0    b c ∵点 ， 1 b b ∴ b ， ∴点C在点B的左侧， A0,c b2 c ∵ ， ， 第18页/共23页 学科网（北京）股份有限公司 1 1  A  0,b2 B   b b , b2   b0 ∴ ，点 ， y kxb2 设直线AB的解析式为 ， 1  1 k b b2   b2  b ∴ ， 1 k  b 解得 b ， 1  y  b xb2   ∴直线AB的解析式为 b  ， 1  y  b bb2 1   当xb时， b  ， Db,1 ∴ ， CD101 ∴ ，是定值． 1 b0, 0 ②∵ b ， 2  1  1 b  0   b 2 ∴  b  即 b ， 1 1æ 1ö 1 S = CD´ B = ç çb+ ÷ ÷³ ´ 2=1 VABC 2 x 2 çè b ÷ø 2 ∴ ， ∴ VABC面积的最小值为1． 【点睛】本题考查了一元二次方程根的判别式，求方程的解，一次函数的解析式，完全平方式的性质，熟 练掌握根的判别式，解析式的确定，完全平方式的非负性是解题的关键． 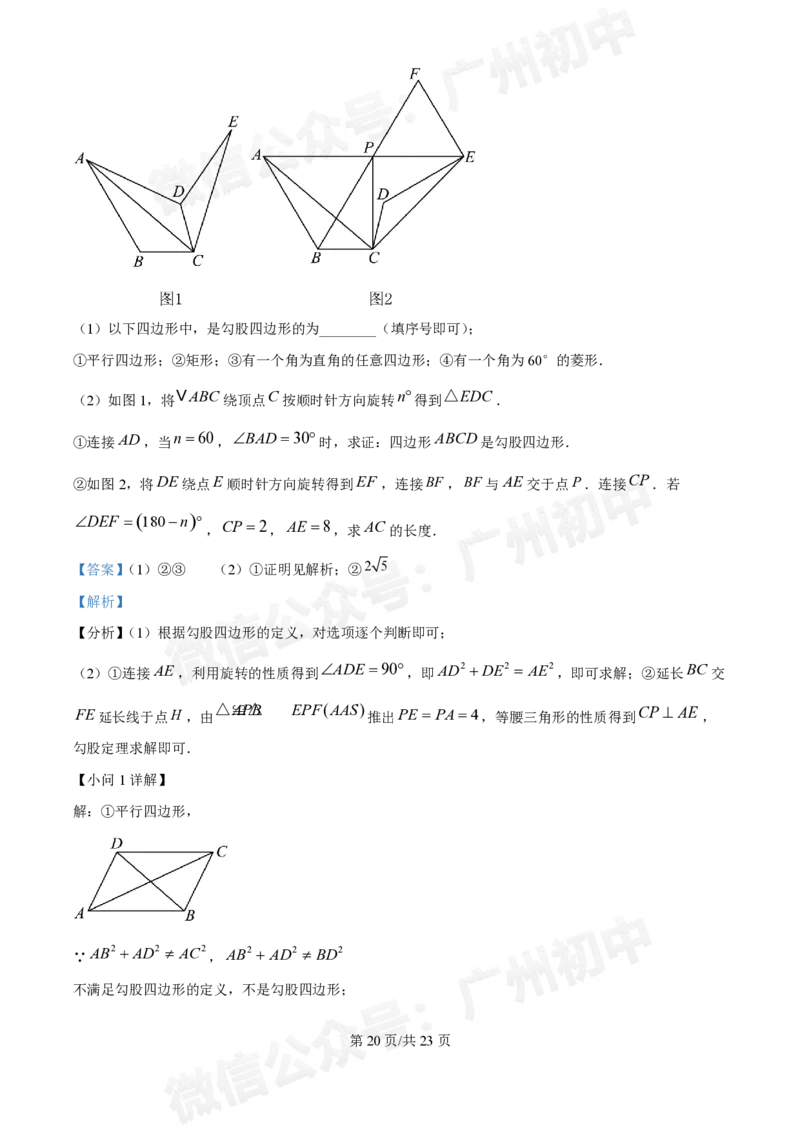25. 给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股 四边形． 第19页/共23页 学科网（北京）股份有限公司（1）以下四边形中，是勾股四边形的为________（填序号即可）； ①平行四边形；②矩形；③有一个角为直角的任意四边形；④有一个角为60°的菱形． （2）如图1，将 VABC绕顶点C按顺时针方向旋转 n 得到 △EDC ． ①连接AD，当 n60 ， BAD30 时，求证：四边形 ABCD 是勾股四边形． ②如图2，将DE绕点E顺时针方向旋转得到EF ，连接BF ，BF 与AE交于点P．连接 CP ．若 DEF 180n CP2 AE 8 AC ， ， ，求 的长度． 【答案】（1）②③ （2）①证明见解析；②2 5 【解析】 【分析】（1）根据勾股四边形的定义，对选项逐个判断即可； （2）①连接AE，利用旋转的性质得到 ADE 90 ，即AD2 DE2  AE2 ，即可求解；②延长BC交 FE延长线于点H ，由 △≌AP△B EPF(AAS) 推出PE  PA4，等腰三角形的性质得到 CP AE ， 勾股定理求解即可． 【小问1详解】 解：①平行四边形， ∵ AB2  AD2  AC2 ，AB2  AD2  BD2 不满足勾股四边形的定义，不是勾股四边形； 第20页/共23页 学科网（北京）股份有限公司②矩形，由矩形的性质可得： A90 ，所以AB2  AD2  BD2 满足勾股四边形的定义，是勾股四边形； ③有一个角为直角的任意四边形，如图， ÐB=90° AB2 BC2  AC2 则： 满足勾股四边形的定义，是勾股四边形； ④有一个角为60°的菱形， ∵ AB2  AD2  AC2 ，AB2  AD2  BD2 的 不满足勾股四边形 定义，不是勾股四边形； 故答案为：②③ 【小问2详解】 ①连接AE，如图： 由旋转的性质可得： BCDACE 60 ， ABC EDC ， AC CE ，AB DE △ACE 为 AC CE  AE ∴ 等边三角形，即 第21页/共23页 学科网（北京）股份有限公司ABCBCDADCBAD 360 由四边形的内角和性质可得： ABCADC 270 ∴ EDCADC 270 ∴ ADE 90 ∴ ∴AD2 DE2  AE2 ，即 AB2  AD2  AC2 ABCD ∴四边形 是勾股四边形 ②延长BC交FE延长线于点H ，如图： 由题意可得：ABC CDE，DE  EF  AB DEF 180n DCH (180n) ∵ ， DCH DEF ∴ DEF DEH 180 ∵ ， DCH DEH 180 ∴ CDEH 180 ∴ ∵ABC CDE ABCH 180 ∴ ∴AB∥FH ∴F ABP ∵DE  EF  AB，EPF APB △≌AP△B EPF(AAS) ∴ ∴PE  PA4 第22页/共23页 学科网（北京）股份有限公司CACE ∵ CP AE ∴ ∴APC 90， AC  AP2 PC2 2 5 ∴ 【点睛】此题是几何变换综合题，考查了勾股定理、旋转的性质、等边三角形的判定和性质、全等三角形 的判定和性质、平行线的判定和性质等知识，解题的关键是理解勾股四边形的定义，学会添加常用辅助线， 构造全等三角形解决问题． 第23页/共23页 学科网（北京）股份有限公司