越秀区广州华侨外国语学校2024-2025学年九年级数学（答案解析）_广州九上月考+期中+期末+一模二模+中考真题_九上月考_初三上十月考

2024 学年第一学期九年级适应性调研 数学问卷 （时间：90分钟，分值：120分） 一、选择题（31030分） 1. 方程x(x-6)=0的解是（ ） A. x=6 B. x =0，x =6 C. x=-6 D. x =0，x =-6 1 2 1 2 【答案】B 【解析】 【分析】利用因式分解法解一元二次方程即可． xx60 【详解】解： ， ∴x60， x0 ， x 0，x 6 ∴ 1 2 ； 故答案为：B． 【点睛】本题考查了一元二次方程的解法，解题关键是熟练运用因式分解法解一元二次方程． x x2 3xm0 2. 已知关于 的方程 的一个根是2，则此方程的另一根为（ ） A. 0 B. 1 C. 2 D. 3 【答案】B 【解析】 x 2x 3 【分析】设方程另一个根为 1，根据根与系数的关系得到 1 ，从而得到方程的另一个根． x 【详解】解：设方程另一个根为 1， ∵a 1， b3 ， b 2x  3 ∴ 1 a ， x 1 解得 1 ， 即此方程的另一个根为1． 故选：B． x x ax2bxc0(a0) 【点睛】本题考查了根与系数的关系：若 1， 2是一元二次方程 的两根时， 第1页/共17页 学科网（北京）股份有限公司b c x x  x x  1 2 a 1 2 a ， ． 3. 每年春秋季节流感盛行，极具传染性如果一人得流感，不加干预，则经过两轮后共有81人得流感，则 x 每人每轮平均会感染几人？设每人每轮平均感染 人，则下列方程正确的是（ ） 1xx2 81 x12 81 A. B. 1xx12 81 1x11x2 81 C. D. 【答案】B 【解析】 【分析】设每人每轮平均感染x人，根据“两轮传染后共有81人患了流感”列出方程即可． x 【详解】设每人每轮平均感染 人，由题意得， x（x+1）+x+1=81， x12 81 即 ． x12 81 故答案为： ． 【点睛】本题考查了一元二次方程的运用，关键是读懂题意，找出题目中的等量关系，列出方程，本题的 等量关系是两轮传染后共有81人患了流感． m x2 6x20 2m2 12m 4. 已知 是方程 的一个根，则 的值为（ ） A. 4 B. 4 C. 2 D. 2 【答案】B 【解析】 m x2 6x20 m2 6m2 2m2 12m 【分析】把 代入 可得， ，然后代入 求解即可． m x2 6x20 m2 6m20 【详解】解：把 代入 得， ， m2 6m2 ∴ ， 2  m2 6m  4 2m2 12m ∴ = ， 故选B． 【点睛】本题考查了一元二次方程的根，以及求代数式的值，运用整体代换，往往能使问题得到简化． y 5x2 5. 若将抛物线 先向右平移2个单位，再向上平移1个单位，得到的新抛物线的表达式为（ ） y 5x22 1 y 5x22 1 A. B. 第2页/共17页 学科网（北京）股份有限公司y 5x22 1 y 5x22 1 C. D. 【答案】A 【解析】 【分析】根据二次函数“上加下减，左加右减”的平移规律进行求解． y 5x2 【详解】解：将抛物线 先向右平移2个单位，再向上平移1个单位，得到的新抛物线的表达式为 y 5x22 1 ， 故选A． 【点睛】本题主要考查了二次函数图象的平移，熟知二次函数图象的平移规律是解题的关键． x x2 4xk 0 k 6. 关于 的一元二次方程 有两个实数根，则 的取值范围是（ ） A. k 4 B. k 4 C. k 4 D. k 4 【答案】B 【解析】 【分析】根据一元二次方程根的判别式可直接进行求解． x x2 4xk 0 【详解】∵关于 的一元二次方程 有实数根，可得： b2 4ac164k 0 ∴ ， k 4 解得： ； 故选：B． 【点睛】本题主要考查一元二次方程根的判别式，熟练掌握一元二次方程根的判别式是解题的关键． 7. 已知x 、x 、是一元二次方程x2+x-2=0的两个根，则x +x +x x 的值为（ ） 1 2 1 2 1 2 A 1 B. -3 C. 3 D. -2 . 【答案】B 【解析】 【分析】根据根与系数的关系求得x +x +，x x 的值，然后将其代入所求的代数式进行求值即可. 1 2 1 2 的 【详解】.解：∵x 、x 、是一元二次方程x2+x-2=0 两个根 1 2 ∴x +x =-1，x ·x =-2 1 2 1 2 ∴原式=-1-2=-3. 故答案为：B. 【点睛】本题考查了根与系数的关系，将根与系数的关系与代数式变形相结合解题是一种经常使用的解题 第3页/共17页 学科网（北京）股份有限公司方法. y x22 2 8. 抛物线 与y轴的交点坐标是（ ） 2，2 0，6 0，2 0，4 A. B. C. D. 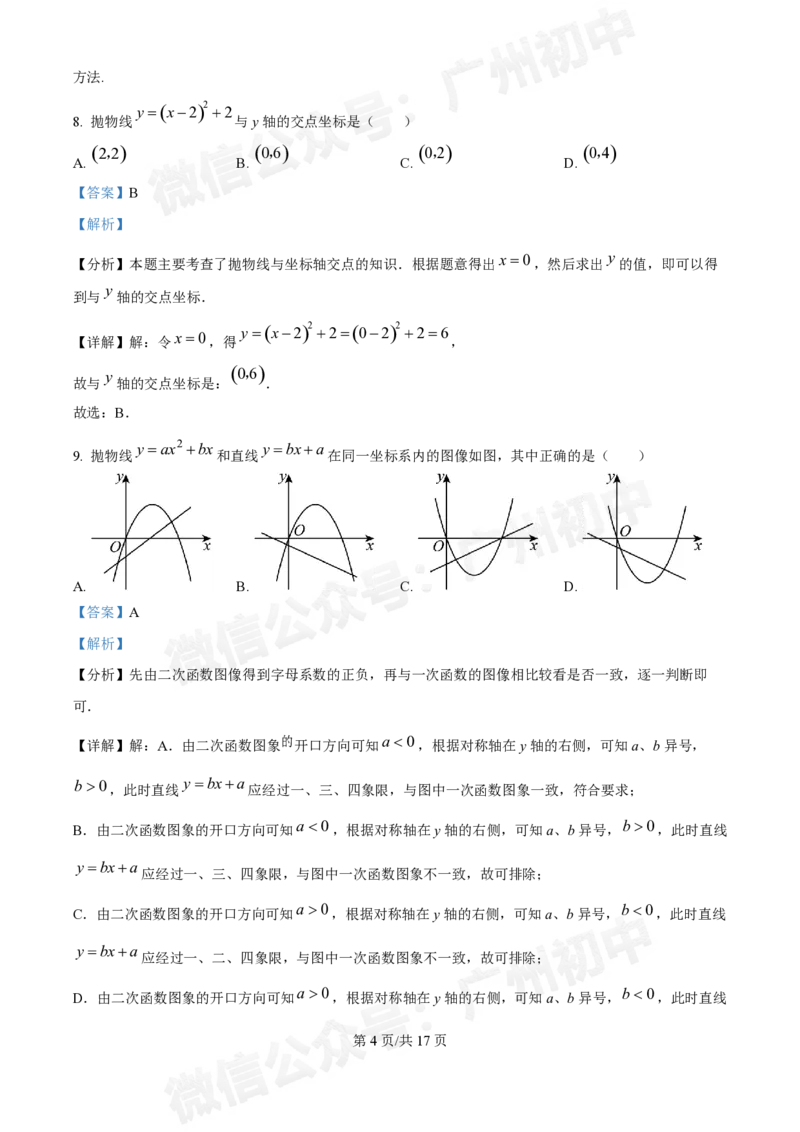【答案】B 【解析】 x0 y 【分析】本题主要考查了抛物线与坐标轴交点的知识．根据题意得出 ，然后求出 的值，即可以得 y 到与 轴的交点坐标． y x22 2022 26 x0 【详解】解：令 ，得 ， y 0，6 故与 轴的交点坐标是： ． 故选：B． y ax2 bx y bxa 9. 抛物线 和直线 在同一坐标系内的图像如图，其中正确的是（ ） A. B. C. D. 【答案】A 【解析】 【分析】先由二次函数图像得到字母系数的正负，再与一次函数的图像相比较看是否一致，逐一判断即 可． 【详解】解：A．由二次函数图象 的 开口方向可知a0，根据对称轴在y轴的右侧，可知a、b异号， b0 y bxa ，此时直线 应经过一、三、四象限，与图中一次函数图象一致，符合要求； B．由二次函数图象的开口方向可知a0，根据对称轴在y轴的右侧，可知a、b异号， b0 ，此时直线 y bxa 应经过一、三、四象限，与图中一次函数图象不一致，故可排除； C．由二次函数图象的开口方向可知 a0 ，根据对称轴在y轴的右侧，可知a、b异号，b0，此时直线 y bxa 应经过一、二、四象限，与图中一次函数图象不一致，故可排除； D．由二次函数图象的开口方向可知 a0 ，根据对称轴在y轴的右侧，可知a、b异号，b0，此时直线 第4页/共17页 学科网（北京）股份有限公司y bxa 应经过一、二、四象限，与图中一次函数图象不一致，故可排除； 故选D． 【点睛】本题主要考查一次函数、二次函数图像与系数的关系，解题的关键是能够根据函数图象判断解析 式中系数的正负． Pm,n Q3,0 y kxb k 0 10. 已知点 ， 都在一次函数 （k，b是常数， ）图象上，（ ） mn 9 mn 9 A. 若 有最大值4，则k的值为 B. 若 有最小值4，则k的值为 mn 9 mn 9 C. 若 有最大值 ，则k的值为4 D. 若 有最小值 ，则k的值为4 【答案】D 【解析】 【分析】本题考查一次函数图象上点的坐标特征，二次函数的最值问题，由题意得到 3 9 mnm（k）m（）3k k m2 3m k(m )2  k 2 4 ，当k 0， mn 有最小值，求出k的值，当 k 0 ， mn 有最大值，求出k的值，即可解决问题． Pm,n Q3,0 y kxb k 0 【详解】解：∵点 ， 都在一次函数 （k，b是常数， ）图象上 kmbn,3kb0 ∴ ， b3k, ∴ nkmbkm3k, ∴ 3 9 mnm（）km（）3k k m2 3m k(m )2  k 2 4 ∴ ， 9  k 当 k 0 时， mn 有最大值 4 ， 9 16  k=4 k  若 mn 有最大值4， 4 ，则 9 ，故A不符合题意； 9  k=9 若 mn 有最大值 9 ， 4 ，则k 4，此时k＞ 0，故C不符合题意； 9  k 当k 0时， mn 有最小值 4 ， 第5页/共17页 学科网（北京）股份有限公司9 16  k 4 k  若 mn 有最小值4， 4 ，则 9 ，故B不符合题意； 9  k=9 若 mn 有最小值 9 ， 4 ，则k 4，故D符合题意． 故选：D． 二、填空题（3618分） y  x2 4x5 11. 抛物线 的顶点坐标是________． 【答案】(2, 1) 【解析】 【分析】利用配方法得出二次函数顶点式形式，即可得出二次函数顶点坐标． y  x2 4x5 【详解】 x2 4x445 = x22 1 ， Q抛物线开口向上，当x= 2时，y = 1， 最小 顶点坐标是：(2, 1)， 故答案为：(2, 1)． 【点睛】此题主要考查了配方法求二次函数顶点坐标，根据题意正确的将二次函数进行配方是解决问题的 关键． y (x2)2 12. 把二次函数 的图像沿y轴向上平移1个单位长度，与y轴的交点为C，则C点坐标是 ． 0,5 【答案】 【解析】 【分析】本题考查二次函数图像的平移及其与坐标轴的交点，熟练掌握抛物线的平移规律是解题的关 键．先根据抛物线的平移规律得到平移后的二次函数的解析式，即可求得图像与y轴的交点C的坐标． y (x2)2 【详解】解：把二次函数 的图像沿y轴向上平移1个单位长度得到新图像的解析式为： 𝑦=(𝑥+2)2+1 y 022 15 x0 当 时， ， 0,5 所以C点坐标是 ． 第6页/共17页 学科网（北京）股份有限公司13. 某药品原价是100元，经连续两次降价后，价格变为64元，如果每次降价的百分率是一样的，那么每 次降价的百分率是_______ 【答案】20％ 【解析】 【分析】此题可设每次降价的百分率为x，第一次降价后价格变为100（1-x）元，第二次在第一次降价后 的基础上再降，变为100（1-x）（1-x），即100（1-x）2元，从而列出方程，求出答案． 【详解】设每次降价的百分率为x，第二次降价后价格变为100（1-x）2元． 根据题意，得100（1-x）2=64， 即（1-x）2=0.64， 解得x =1.8，x =0.2． 1 2 因为x=1.8不合题意，故舍去， 所以x=0.2． 即每次降价的百分率为0.2，即20%． 故答案为20%． A1,y ,B1,y ,C4,y  y x32 k y ,y ,y 14. 已知 1 2 3 三点都在二次函数 的图象上，则 1 2 3的大小 关系为___________ y  y  y y  y  y 【答案】 1 2 3## 3 2 1 【解析】 x3 【分析】本题考查了根据二次函数的图象和性质，根据解析式可得二次函数的对称轴为直线 ，二次 函数图象开口向下，进而根据点距离对称轴越远，函数值越小，即可求解． 10 【详解】解：∵ ， ∴二次函数图象开口向下， y x32 k ∵ ， x3 ∴二次函数的对称轴为直线 ， y x32 k A1,y ,B1,y ,C4,y  ∵抛物线 的图象上有三个点 1 2 3 ， 13 4,13 2, 43 1 ， y  y  y ∴ 1 2 3， 第7页/共17页 学科网（北京）股份有限公司y  y  y 故答案为： 1 2 3 kx2 2x10 15. 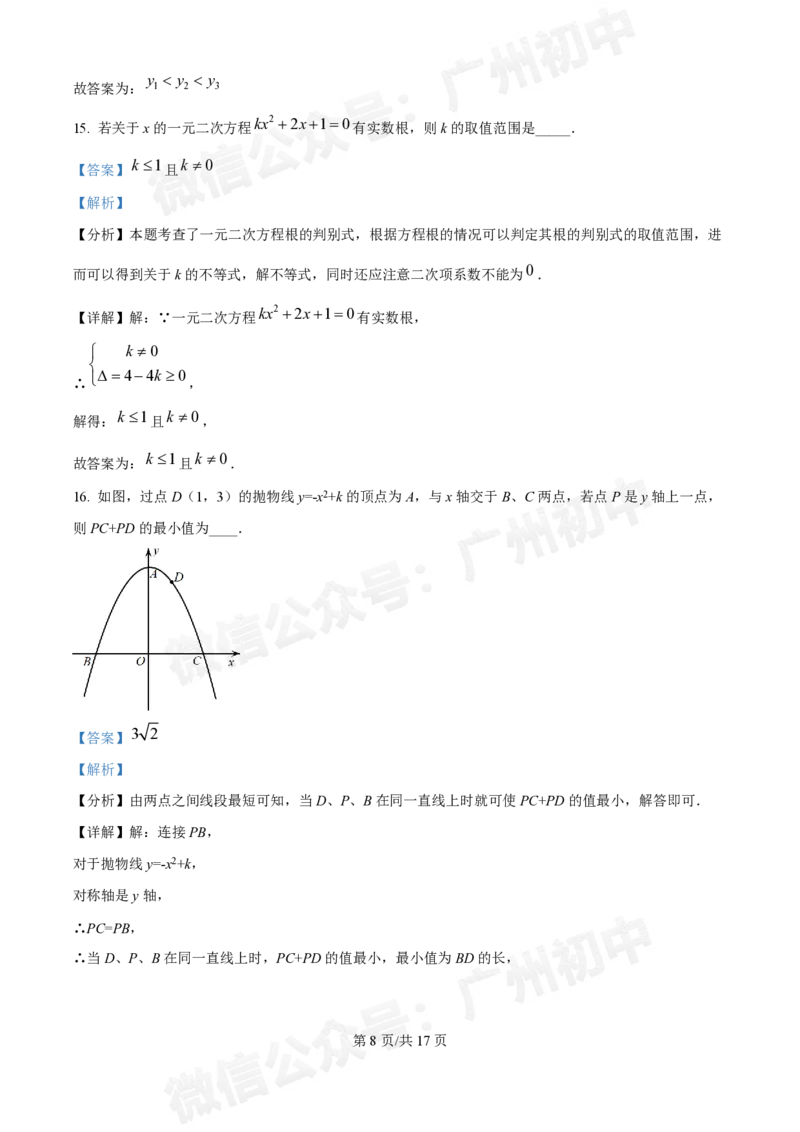若关于x的一元二次方程 有实数根，则k的取值范围是_____． k 1 k 0 【答案】 且 【解析】 【分析】本题考查了一元二次方程根的判别式，根据方程根的情况可以判定其根的判别式的取值范围，进 0 而可以得到关于k的不等式，解不等式，同时还应注意二次项系数不能为 ． kx2 2x10 【详解】解：∵一元二次方程 有实数根，  k 0  44k 0 ∴ ， k 1 k 0 解得： 且 ， k 1 k 0 故答案为： 且 ． 16. 如图，过点D（1，3）的抛物线y=-x2+k的顶点为A，与x轴交于B、C两点，若点P是y轴上一点， 则PC+PD的最小值为____． 3 2 【答案】 【解析】 【分析】由两点之间线段最短可知，当D、P、B在同一直线上时就可使PC+PD的值最小，解答即可． 【详解】解：连接PB， 对于抛物线y=-x2+k， 对称轴是y轴， ∴PC=PB， ∴当D、P、B在同一直线上时，PC+PD的值最小，最小值为BD的长， 第8页/共17页 学科网（北京）股份有限公司∵抛物线y=-x2+k过点D（1，3）， ∴把x=1，y=3代入y=-x2+k，解得：k=4， 把y=0代入y=-x2+4，解得：x=2或x=-2， 所以点B的坐标为（-2，0）， (21)2 32 3 2 所以BD= ， 3 2 故答案为： ． 【点睛】本题考查了抛物线与x轴的交点，轴对称－最短路线问题，找到P点是本题的关键． 三、解答题共（共72分） 17. 解下列方程： 2x 3x(x2) （1） x2 2x30 （2） ． 1 x  【答案】（1） 1 3， x 2 2 x 3 x 1 （2） 1 ， 2 【解析】 【分析】本题考查了解一元二次方程，解题的关键在于灵活选取适当的方法解方程． （1）利用因式分解法法求解即可； （2）利用因式分解法法求解即可. 【小问1详解】 2x 3x(x2) 解： 3x(x2)(x2)0 方程化为： ，， (3x1)(x2)0 ∴ ， 第9页/共17页 学科网（北京）股份有限公司3x10 x20 ∴ 或 ； 1 x  ∴ 1 3， x 2 2 ． 【小问2详解】 x2 2x30 解： (x3)(x1)0 ∴ ， x30 x10 ∴ 或 ， x 3 x 1 ∴ 1 ， 2 ． 18. 已知关于x的方程：x2﹣（6+m）x+9+3m＝0． （1）求证：无论m为何值，方程都有实数根． （2）若该方程的两个实数根恰为斜边为5的直角三角形的两直角边长，求m的值． 【答案】（1）见解析；（2）m的值是1． 【解析】 【分析】（1）求出根的判别式，再根据非负数的性质即可证明； （2）根据一元二次方程根与系数的关系即可求得方程两根的和与两根的积，两根的平方和可以用两根的 和与两根的积表示，即可得到一个关于m的方程，求得m的值． 【详解】（1）证明：对于关于x的方程x2-（6+m）x+9+3m=0， a 1 b（6）m c93m ∵ ， ， ， Vb2 4ac ∴ =（6+m）2-4（9+3m）=m2≥0， ∴无论m为何值方程都有两个实数根； （2）解：∵直角三角形的两直角边AB、AC的长是该方程的两个实数根， ∴AB+AC=m+6，AB•AC=9+3m， ∵△ABC是直角三角形， ∴AB2+AC2=BC2， ∴（AB+AC）2-2AB•AC=BC2， 即（m+6）2-2×（9+3m）=52， 解得：m=-7或m=1， 又∵AB•AC=9+3m，m为正数， 第10页/共17页 学科网（北京）股份有限公司∴m的值是1． 【点睛】本题主要考查了勾股定理，一元二次方程的根与系数的关系，根的判别式以及运用公式法解一元 二次方程，考查的知识点较多，但难度不大． y ax2 bxc 19. 抛物线 上部分点的横坐标x，纵坐标y，的对应值如下表： 2 x … 1 0 1 2 … 4 4 y … 0 0 8 … （1）根据上表填空： ①抛物线经过点（3，__________），对称轴为__________； y0 ②当 时，x取值范围是__________； y ax2 bxc （2）求该抛物线 的解析式． 1 x 【答案】（1）①8，直线 2；② 2