越秀区第十六中学2024-2025学年九年级数学10月月考试题_广州九上月考+期中+期末+一模二模+中考真题_九上月考_初三上十月考

2024 学年第一学期十六中教育集团阶段教学质量反馈 九年级数学（问卷） 一、选择题（每小题3分，共30分） 1. 下列图标中，既是轴对称图形，又是中心对称图形的是（ ） A B. . C. D. y 2(x1)2 6 2. 抛物线 的顶点坐标为（ ） (1,6) (1,6) (1,6) (1,6) A. B. C. D. x2 x10 3. 一元二次方程 的根的情况是（ ） A. 没有实数根 B. 有两个相等的实数根 C. 有两个不相等的实数根 D. 有一个实数根 x2 2x50 4. 用配方法解方程 时，原方程应变形为（ ） x12 6 x12 6 x22 9 x22 9 A. B. C. D. 5. 某同学在用描点法画二次函数的图象时，列出了下面的表格： 2 x …… 1 0 1 2 3 …… 3 4 3 y …… 5 0 m …… 那么m的值为（ ） A. 3 B. 4 C. 0 D. 5 第1页/共6页 学科网（北京）股份有限公司y 5x2 6. 把抛物线 向左平移2个单位，再向上平移3个单位，得到的抛物线是（ ） y5x22 3 y5x22 3 y5x22 3 y5x22 3 A. B. C. D. 7. 若  ，  是方程x2 2x10的两根，则  的值为（ ） A. 1 B. -1 C. 3 D. -3 8. 有两个直角三角形纸板，一个含45°角，另一个含30°角，如图①所示叠放，先将含30°角的纸板固 定不动，再将含45°角的纸板绕顶点A顺时针旋转，使BC∥DE，如图②所示，则旋转角∠BAD的度数 为（ ） A 15° B. 30° C. 45° D. 60° . 9. 如图，幼儿园计划用30m的围栏靠墙围成一个面积为100m2的矩形小花园（墙长为15m），则与墙垂直 的边x为（ ） A. 10m或5m B. 5m或8m C. 10m D. 5m △BCD BC 10. 如图，BD为矩形ABCD的对角线，将△BCD沿BD翻折得到 ， 与边AD交于点E．若 AB＝x ，BC＝2x ，DE＝3，其中x 、x 是关于x的方程x2﹣4x+m＝0的两个实根，则m的值是（ 1 2 1 2 ） 16 12 5 5 A. B. C. 3 D. 2 二、填空题（每小题3分，共18分） 第2页/共6页 学科网（北京）股份有限公司x2 y  11. 函数 x1 中，自变量x的取值范围是__________． VABO OB VABO 30 12. 如图，边长为2的等边 的边 在x轴上，将 绕原点O逆时针旋转 得到三角形 OAB A 1 1，则点 1的坐标为________． 13. 若y=（a-1）x3a2−1是关于x的二次函数，则a=________ 14. 抛物线 y 2x2 bx3的 对称轴是直线 x1 ，则b的值为___． x2 x10 20262a2 2a 15. 若a是方程 的一个根，则代数式 的值是__________． y ax2 bxca0 3,0 x  2 16. 如图，抛物线 的对称轴为直线 ，抛物线与x轴的一个交点在 和 4,0 之间，其部分图象如图所示．有下列结论： 4ab0 c0 3ac0 ① ；② ；③ ；  9   5   1   ,y  ,y  ,y        2 1   2 2   2 3  y  y  y ④若 ， ， 是该抛物线上的三点，则 1 2 3； 4a2bat2 bt ⑤ （t为实数）． 其中正确结论的序号有__________． 三、解答题（本大题共9题，共72分） x2 4x30 17. 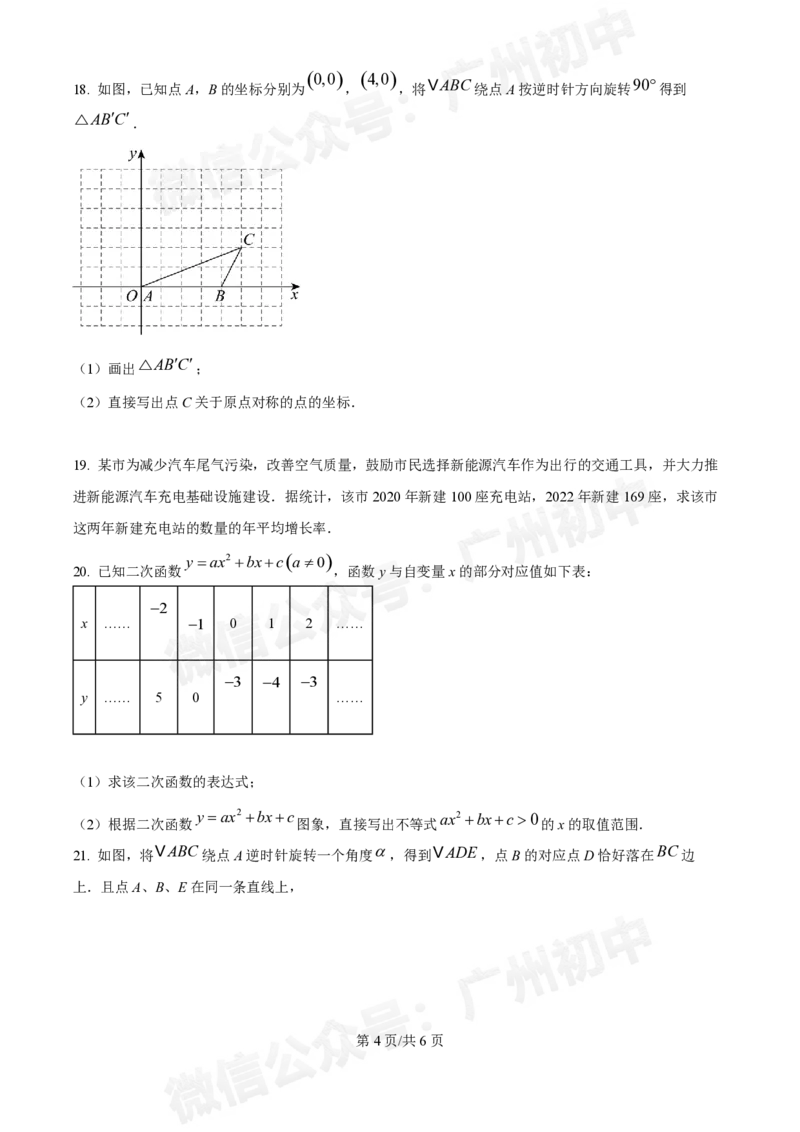解方程： ． 第3页/共6页 学科网（北京）股份有限公司0,0 4,0 18. 如图，已知点A，B的坐标分别为 ， ，将 VABC绕点A按逆时针方向旋转 90 得到 △ABC ． （1）画出△ABC ； （2）直接写出点C关于原点对称的点的坐标． 19. 某市为减少汽车尾气污染，改善空气质量，鼓励市民选择新能源汽车作为出行的交通工具，并大力推 进新能源汽车充电基础设施建设．据统计，该市2020年新建100座充电站，2022年新建169座，求该市 这两年新建充电站的数量的年平均增长率． y ax2 bxca 0 20. 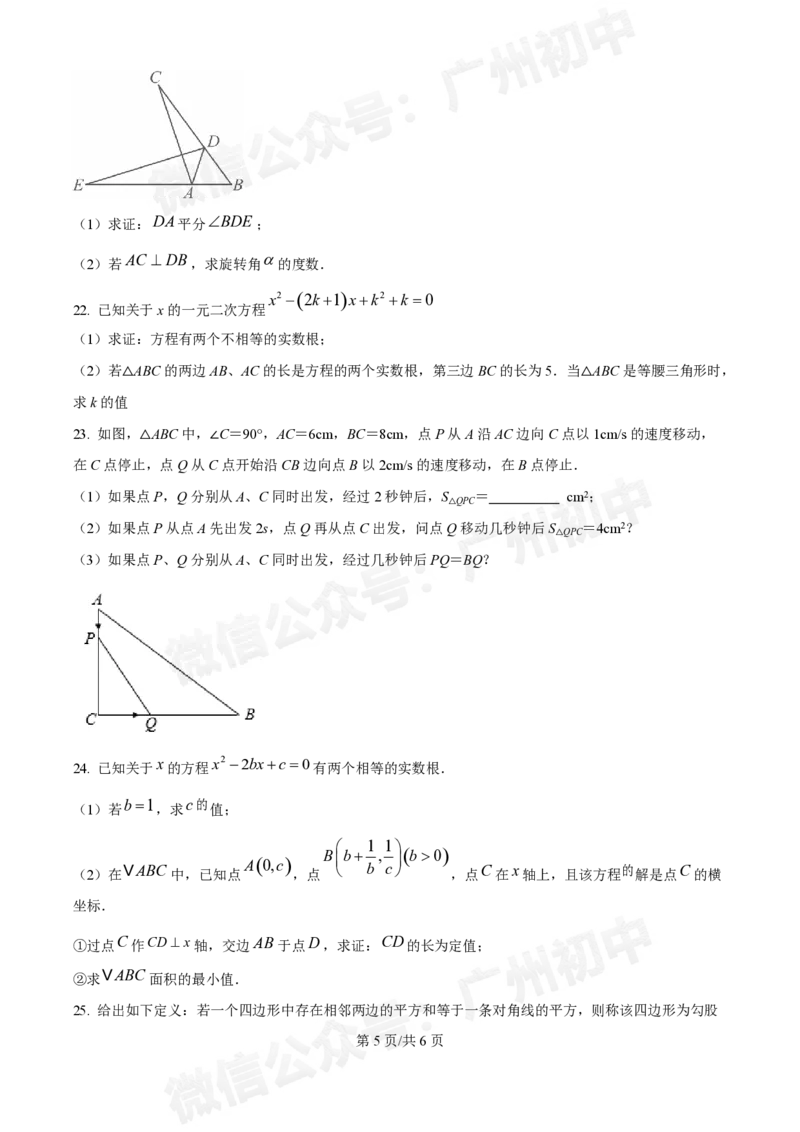已知二次函数 ，函数y与自变量x的部分对应值如下表： 2 x …… 1 0 1 2 …… 3 4 3 y …… 5 0 …… （1）求该二次函数的表达式； y ax2 bxc ax2 bxc0 （2）根据二次函数 图象，直接写出不等式 的x的取值范围． 21. 如图，将 VABC绕点A逆时针旋转一个角度  ，得到VADE，点B的对应点D恰好落在BC边 上．且点A、B、E在同一条直线上， 第4页/共6页 学科网（北京）股份有限公司（1）求证：DA平分BDE； AC  DB  （2）若 ，求旋转角 的度数． x2 2k1xk2 k 0 22. 已知关于x的一元二次方程 （1）求证：方程有两个不相等的实数根； （2）若△ABC的两边AB、AC的长是方程的两个实数根，第三边BC的长为5．当△ABC是等腰三角形时， 求k的值 23. 如图，△ABC中，∠C＝90°，AC＝6cm，BC＝8cm，点P从A沿AC边向C点以1cm/s的速度移动， 在C点停止，点Q从C点开始沿CB边向点B以2cm/s的速度移动，在B点停止． （1）如果点P，Q分别从A、C同时出发，经过2秒钟后，S ＝ cm2； △QPC （2）如果点P从点A先出发2s，点Q再从点C出发，问点Q移动几秒钟后S ＝4cm2？ △QPC （3）如果点P、Q分别从A、C同时出发，经过几秒钟后PQ＝BQ？ x x2 2bxc0 24. 已知关于 的方程 有两个相等的实数根． b1 c的 （1）若 ，求 值；  1 1 B b , b0 （2）在 VABC中，已知点 A0,c ，点   b c   ，点C在 x 轴上，且该方程 的 解是点C的横 坐标． ①过点C作CDx轴，交边AB于点D，求证： CD 的长为定值； ②求 VABC面积的最小值． 25. 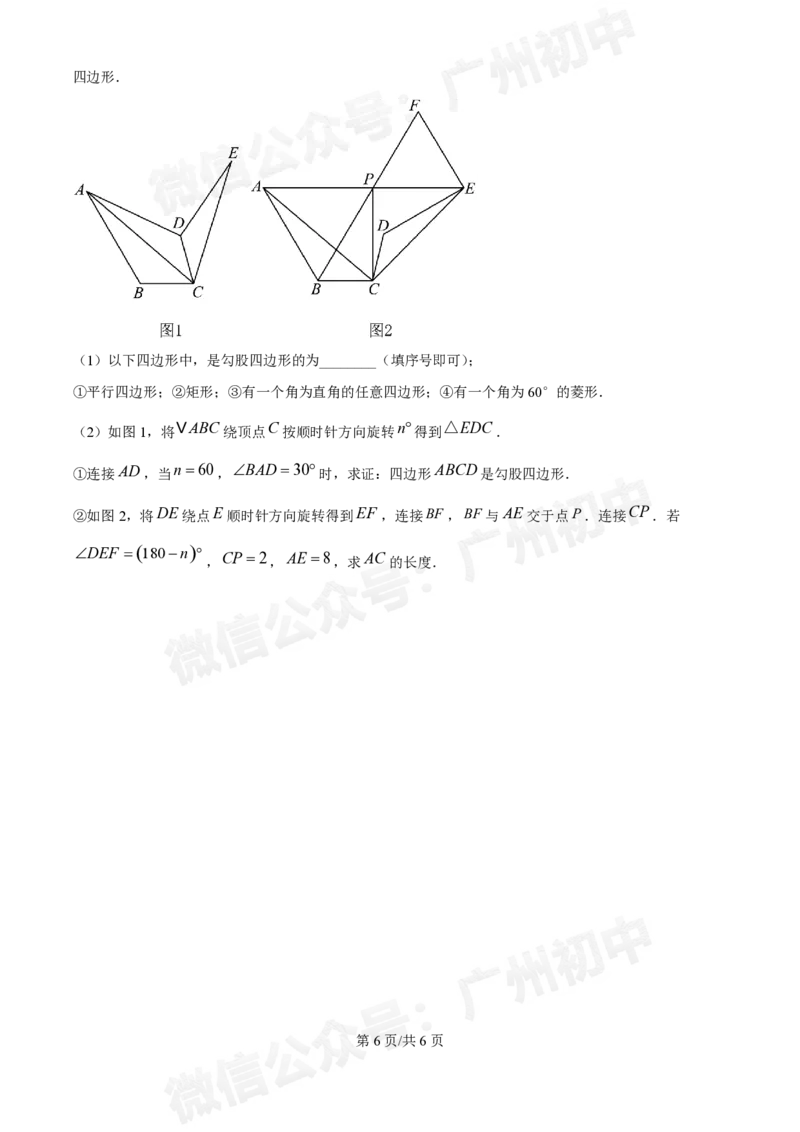给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股 第5页/共6页 学科网（北京）股份有限公司四边形． （1）以下四边形中，是勾股四边形的为________（填序号即可）； ①平行四边形；②矩形；③有一个角为直角的任意四边形；④有一个角为60°的菱形． （2）如图1，将 VABC绕顶点C按顺时针方向旋转 n 得到 △EDC ． ①连接AD，当 n60 ， BAD30 时，求证：四边形 ABCD 是勾股四边形． ②如图2，将DE绕点E顺时针方向旋转得到EF ，连接BF ，BF 与AE交于点P．连接 CP ．若 DEF 180n CP2 AE 8 AC ， ， ，求 的长度． 第6页/共6页 学科网（北京）股份有限公司