文档内容
方法精讲-资料 2
(笔记)
主讲教师:戚七
授课时间:2024.03.14
粉笔公考·官方微信方法精讲-资料 2(笔记)
学习任务:
1.课程内容:一般增长率、增长量
2.授课时长:3小时
3.对应讲义:第167~180页
4.重点内容:
(1)增长率相关术语的联系与区别
(2)一般增长率的题型识别及计算公式
(3)一般增长率的比较技巧
(4)增长量的计算与比较技巧
【注意】昨天讲解了速算和基期现期,对资料分析打了基础。今天讲解一般
增长率和增长量,难度不大,但是比较细、比较多,所以一定要跟着老师的思维。
第三节 一般增长率
基本术语:
一般增长率
1.基本术语
(1)增长率
(2)百分数与百分点
(3)增长率与倍数
(4)成数与翻番
(5)增幅、降幅与变化幅度
2.一般增长率计算
3.一般增长率比较
【解析】一般增长率:非常重要。
1.基本术语:
(1)增长率。
1(2)百分数与百分点。
(3)增长率与倍数。
(4)成数与翻番。
(5)增幅、降幅与变化幅度。
2.一般增长率计算。
3.一般增长率比较。
增长率
增长率是用来表述基期量与现期量变化的相对量。增长率又称增速、增幅或
者增长幅度、增值率等,增长率为负时表示下降,下降率也可直接写成负的增长
率。
【解析】增长率(常用r表示):
1.增长率表述现期量与基期量变化的相对量,是一个比值,增长率就是现期
相对基期而言的幅度,一般用r 表示。增长率r=增长量/基期量。
2.增长率又称增速、增幅或者增长速度、增长幅度、增值率等。增幅中的“幅”
是幅度,对应比值,所以也对应增长率。
3.增长率为负时表示下降,下降率也可直接写成负的增长率。
4.例:下降5%。本质含义就是增长率是-5%。
百分数与百分点
百分数:用来反映量之间的比例关系。
百分点:用来反映百分数的变化。
【解析】百分数与百分点:平时生活中提到百分数比较多。
1.百分数(%)表示两个量的比例关系,用除法计算。
引例:甲班共有50人,女生人数30人,问女生占全班人数的比重?
答:结合生活常识,谁占谁的比重,用部分除以整体,即30/50=60%,是除
法形式。
2.百分点表示百分数的变化,用加减法计算。
引例:甲班女生占全班人数的比重为 60%,乙班女生占比为 30%,问甲班女
2生所占比重比乙班多几个百分点?
答:平时比较习惯说 60%-30%=30%,但是这样表示不严谨,而是相差 30 个
百分点;题目出现百分点,本质是百分数之间的差值,一般用加减法计算。
增长率与倍数
增长率指比基期量多出的比率,倍数指两数的直接比值。
若A是B的n倍,则n=r+1(r指A相对于B的增长率)。
【解析】倍数与增长率:
1.倍数:两数的直接比值。A 是B的多少倍,两个数字直接做除法,倍数=A/B。
2.增长率:现期比基期多出的比率。
(1)A比B多/增长多少(%),增长量=A-B,则增长率=A-B/B=A/B-B/B=A/B-1,
和 A/B 中间差 1,则倍数和增长率之间差 1,如果题干给出增长率为 30%,则倍
数为30%+1=1.3倍。如果给出今年是去年的2.5倍,问增长率是多少,对应150%。
(2)A比B多/增长多少倍,增长倍数=是几倍-1=A/B-1,而增长率也是A/B-1,
则增长+倍数,就是增长率问题。题干出现倍数,需要看清楚,如果是“是几倍”,
就是增长率+1,如果题干问增长+倍数,就是增长率问题;比如今年比去年增长
1.3倍,增长率就是1.3,即130%;今年是去年的1.3+1=2.3倍。
3.例:今年1500元,去年500 元。
(1)今年是去年的()倍。
答:1500/500=3倍。
(2)今年比去年增长了()%。
答:(1500-500)/500=200%,则增长率为200%。
(3)今年比去年增长/多了()倍。
答:今年是去年的3倍,则去年是 1,今年是3,多了3-1=2倍。
成数与翻番
成数:几成相当于十分之几。
翻番:翻一番为原来的2倍,翻两番为原来的4倍,以此类推,翻n番为原
来的2n倍。
3【解析】成数与翻番:
1.成数:几成相当于十分之几。比如增长几成,谁占谁几成;十分之几就是
百分之几十,比如增长2成,对应2/10,即20%;比如占比占了3成,比重就是
30%。
2.翻番:翻n番是原来的2n倍。
3.翻1番:需要在原来的基础上乘以一个2,是原来的2倍;翻2番:是在
原来的基础上乘以两个2,是原来的2*2倍;翻3番:是在原来的基础上乘以2*2*2,
是原来的2*2*2倍。对于番数,题干问几番,需要先找到现期和基期的倍数,再
看倍数可以转化为2的几次方。
4.例:从200到1600,翻了几番?
答:出现翻番先找倍数,倍数=1600/200=8倍,是2³,则是翻三番。
增幅、降幅与变化幅度
增幅一般就是指增长率,有正有负。
降幅指下降的幅度,降幅比较大小时,只比较增长率的绝对值(前提必须为
下降)。
变化幅度指增长或下降的绝对比率,变化幅度比较大小时,用增幅(降幅)
的绝对值。
【解析】“增幅”、“降幅”、“变化幅度”:
1.增幅(=增长率=增速),(r可正可负、r带着符号比),增幅就是增长率,
对应r,增长可以是正增长,也可以是负增长,则是可正可负的,比较的过程中,
正数大于负数,则增幅比较是带着符号比较的,比如3%>-5%。
2.降幅(r=-30%→降幅为30%)。(r 必须为负、比较 r的绝对值)。“降”对
应“下降”,生活中没有描述正下降和负下降的,则出现“降”,增长率是小于0
的,比如增长率是-30%,可以表述为下降30%,或者降幅为30%,“降”表示负数;
比如一个是减少 10%,另一个是减少 20%,比较的时候会发现 20%更快,即比较
的时候看绝对值。
3.变化幅度(r可正可负、比较 r 的绝对值)。变化可以是上升,也可以是
下降,所以是可正可负的,上升 10%,变化幅度是 10%,下降 10%,变化幅度也
4是10%,所以变化幅度中,正负不重要,只看绝对值。
4.在增长率A.10%、B.-20%、C.30%、D.-40%中:
(1)增幅最大的是(),最小的是()。
答:有两个正的,两个负的,正的大于负的,再比较两个正数,30%>10%,
则增幅最大的是 C 项;找增幅最小的,需要看两个负数,-40%<-20%,对应 D
项。
(2)降幅最大的是(),最小的是()。
答:在选项中,A、C 项不参与比较,因为是正数,不能参与降幅比较,再
比较B、D项,看绝对值,B项对应 20%,D项对应 40%,则降幅最大的是 D项,
降幅最小的是B项。
(3)变化幅度最大的是(),最小的是()。
答:在绝对值中,-40%绝对值最大,10%绝对值最小,则变化幅度最大的是
D项,最小的是A项。
5.降幅必须为负,所以增幅必须为正:是错误的,降幅限定了必须是下降,
但是增幅有正增长和负增长,所以增幅是可正可负的。降幅是增幅的一个部分。
6.不可以表述为降幅为-30%,降幅中的“降”就表示负号了,所以不能是-30%。
7.总结:平时用的最多的是增幅,即增长率,增长率的比较是可正可负的,
需要带着符号比较;如果题目出现降幅或者变化幅度,重点关注绝对值比较。
一般增长率
1.基本术语辨析
2.一般增长率计算
3.一般增长率比较
一、计算
增长率计算
识别:增长/下降+%、几成、几倍;
增长速度、增长幅度
题型:①已知一个百分数和百分点
5②已知具体量(现期量、基期量、增长量中至少两个)
识别:给一个增长率和百分点,求另一个增长率
方法:“增长率”直接带符号进行“高减低加”运算
①2020年同比增长30%,增长率比上年提高10个百分点,问:2019年的增
长率?
②2020年同比增长30%,增长率比上年降低10个百分点,问:2019年的增
长率?
③2020年同比增长-30%,增长率比上年提高10个百分点,问:2019年的增
长率?
遇到“提高”类描述用减法、遇到“回落”类描述用加法,简称“高减低加”
【注意】增长率计算:
1.识别:增长/下降+%、几成(百分之几十)、几倍(百分之几百);增长速
度(增长率)、增长幅度(增幅)。
2.题型:根据题干给出的数据不同,选择方法。
(1)已知一个百分数和百分点。
①做法:“增长率”直接带符号进行“高减低加”运算。
②例:
a.2020年同比增长30%,增长率比上年提高10个百分点,问:2019年的增
长率?
答:增长率在 30%的基础上,比上年提高,求上年,需要减去,则 2019年
增长率是30%-10%=20%;出现“提高”,用减法计算。
b.2020年同比增长30%,增长率比上年降低10个百分点,问:2019年的增
长率?
答:2020年增长率是30%,比去年降低,求去年,需要加上,即出现“降低”,
做加法,30%+10%=40%。
c.2020年同比增长-30%,增长率比上年提高10个百分点,问:2019年的增
长率?
答:提高10个百分点,需要做减法,题干给出“增长率比上年提高10个百
分点”,增长率需要带着符号,则 2020 年的增长率 r=-30%,2019 年增长率
6=-30%-10%=-40%。
(2)已知具体量(现期量、基期量、增长量中至少两个)。
3.注意:遇到“提高”类描述用减法、遇到“回落”类描述用加法,简称“高
减低加”。
2021年H省商品、服务类电子商务交易额为11526.13亿元,比上年同期增
长 21.8%,高于全国增速 2.3 个百分点。H 省跨境电商进出口交易额为 2018.3
亿元,其中,出口 1475.5 亿元,同比增长 15.7%;进口 542.8 亿元,同比增长
16.0%。H 省网上零售额为 2948.2亿元,同比增长 12.5%,其中,实物商品网上
零售额为2426.4亿元,同比增长10.1%。
【例1】(2023国考)2021年,全国商品、服务类电子商务交易额同比增长
了:
A.17.2% B.19.5%
C.21.8% D.24.1%
【解析】1.题干出现增长+%,求增长率,主题词是全国商品、服务类电子商
务交易额,对应材料中“2021年H省商品、服务类电子商务交易额为11526.13
亿元,比上年同期增长 21.8%,高于全国增速 2.3 个百分点”,给出 H 省的增长
率,高于全国增速2.3个百分点,即给出百分数(现期增长率)和百分点,求基
期增长率,“高于”用减法,列式:全国增长率=21.8%-2.3%=19.5%,对应 B项。
【选B】
【注意】
1.易错项D项,D项就是21.8%+2.3%,这是出题人的坑。
2.给增长率和百分点,求基期增长率,对应“高减低加”。
增长率计算(给百分点)——高减低加
易错点区分——降幅变化
①2020年同比下降30%,降幅比去年扩大10个百分点。则2019年的增长率
为:
7问:2020年降幅(),2019年的降幅(),2019年增长率()
②2020年同比下降30%,降幅比去年收窄10个百分点。则2019年的增长率
为:
问:2020年降幅(),2019年的降幅(),2019年增长率()
【注意】易错点区分——降幅变化:
1.例:2020年同比下降30%,降幅比去年扩大10个百分点。则2019年的增
长率为?
答:给出“降幅比去年扩大 10个百分点”,2020年降幅是30%(因为“降”
表示负号),出现“扩大”,用减法,2019 年的降幅=30%-10%=20%,题干问增长
率,加负号,2019年的增长率=-20%。
2.例:2020年同比下降30%,降幅比去年收窄10个百分点。则2019年的增
长率为:
答:今年的降幅是30%,“收窄”是降低的表述,用加法,2020年降幅是30%,
2019年的降幅=30%+10%=40%,2019年的增长率=-40%。
3.“降幅”先用r的绝对值进行“高减低加”运算,算出降幅;再添“负号”
表示增长率。
4.注意:遇到“提高”类描述用减法、遇到“回落”类描述用加法,简称“高
减低加”。
2020年全年,汽车产销降幅收窄至2%以内。汽车产量为2522.5万辆,销量
为2531.1万辆,同比分别下降2.0%和1.9%,降幅分别比2020年上半年收窄14.8
和15.0个百分点。2020年全年,新能源汽车销量为136.7万辆,同比增长10.9%。
【例2】(2021联考)2020年上半年汽车销量降幅估计在:
A.10个百分点以内 B.10~12个百分点
C.12~14个百分点 D.15个百分点以上
【解析】2.问题时间是2020年上半年,材料时间是2020年全年,时间不一
致,圈出时间,问降幅,是增长率的一类,主体是汽车销量,材料给出“汽车产
量为 2522.5万辆,销量为 2531.1万辆,同比分别下降 2.0%和 1.9%,降幅分别
比2020年上半年收窄14.8和15.0 个百分点”,不要错找产量,即销量全年下降
81.9%,降幅比 2020 年上半年收窄了 15 个百分点,计算 2020 年上半年的降幅,
“收窄”用加法,列式:2020年上年降幅=1.9%+15%=16.9%,题干问的就是降幅,
对应D项。【选D】
【注意】如果本题问增长率是多少,需要添负号,则增长率对应-16.9%。
增长率计算(给百分点)——高减低加
“增长率”直接带符号进行“高减低加”运算。
“降幅”先用r的绝对值进行“高减低加”运算,算出降幅;再添“负号”
表示增长率。
常见变化描述积累:
“提高”:上升、增加、扩大、提升等——用“-”
“降低”:下降、减少、缩小、收窄等——用“+”
是否带符号计算,不是增长率的正负决定,而是取决于描述增幅还是降幅在
发生变化
【注意】增长率计算(给百分点):总结,高减低加。
1.“增长率”直接带符号进行“高减低加”运算。
2.“降幅”先用 r的绝对值进行“高减低加”运算,算出降幅;再添“负号”
表示增长率。
3.常见变化描述积累:
(1)“提高”:上升、增加、扩大、提升等——用“-”。
(2)“降低”:下降、减少、缩小、收窄等——用“+”。
4.注意:是否带符号计算,不是增长率的正负决定,而是取决于描述增幅还
是降幅在发生变化。
增长率计算(给具体量)
识别:给现期量/基期量/增长量中至少两个量,求增长率
公式:增长率r=增长量/基期量
【变型】=增长量/(现期量-增长量)=(现期量-基期量)/基期量=现期量/
9基期量-1
速算技巧:截位直除
【注意】增长率计算(给具体量):更常见。
1.识别:给现期量/基期量/增长量中至少两个量,求增长率。
2.公式:增长率 r=增长量/基期量=增长量/(现期量-增长量)=(现期量-
基期量)/基期量=现期量/基期量-1。如果题目给出增长量和现期量,计算增
长率,需要有基期量,可以直接表示增长量/(现期量-增长量);如果题干给
出现期量和基期量,计算增长率,可以用(现期量- 基期量)/基期量,不需
要记公式的变形。
3.速算技巧:截位直除。
【例3】(2023安徽)2021年,全国羊肉产量同比增长率约为:
A.2.4% B.3.4%
C.4.4% D.5.4%
【解析】3.题干时间是2021 年,材料给出了,问同比增长率,同比是和上
一年比较,即和2020年比较,给出现期和基期,求增长率,列式:增长率=增长
量/基期量=(514.1-492.3)/492=21.8/492.3,选项差距大,首位是4,对应C
项。【选 C】
【注意】是否可以列式现期/基期-1:如果用这个公式,列式很简单,是
514.1/492.3-1,但是不好计算,无法一步得出答案,还需要减 1,除法需要计
10算到第三位,很浪费时间。(514.1-492.3)/492计算量远远低于514.1/492.3-1。
【例4】(2020国考)2013~2018年间中国集成电路产业销售额增速最高的
年份,当年集成电路进口金额同比约增加:
A.5% B.10%
C.15% D.20%
【解析】4.题干给出时间段,出现增加+%,是增长率问法,主题词是集成电
路进口金额,题干前面限定了年份,“2013~2018年间中国集成电路产业销售额
增速最高的年份”,销售额对应图二,增速最高的年份是 2017 年,即问 2017 年
集成电路进口金额同比增长多少,给出现期和基期,增长率=增长量/基期=
(2601.4-2270.7)/2270.7≈330/2270,首位商 1,次位接近商 5,对应 C 项。
【选C】
11【例5】(2021江苏)2019年末江苏省金融机构各项存款额度比上年末增长:
A.8.5% B.9.4%
C.10.2% D.10.8%
【解析】5.题干时间是2019年,材料时间也是2019年,出现增长+%,是增
长率问题,主题词是“江苏省金融机构各项存款额度”,给出了现期和增长量,
计算增长率,题干没有给出基期,现期量和增长量的差值就是基期,列式:增长
量/基期量=13089.6/(152837.3-13089.6),一步除法,可以先截位,C、D项选
项差距小,需要截三位,13089.6/(152000-13000),转化为 13089.6/140,首
位商9,次位商4,对应B项。【选B】
【注意】
1.加减法截位需要考虑位数对齐。
2.易错项A项:式子列错为13089.6/152837.3,公式错了,错用增长量/现
期了。
【例6】(2020国考)2011~2018年间,我国海洋主题公园非门票收入同比
12增速超过10%的年份有几个?
A.5 B.6
C.3 D.4
【解析】6.给了时间段2011~2018年,问同比增速超过10%的年份有几个,
主题词是非门票收入,需要计算8个增长率,此类题目是有技巧的。
方法一:做减法:现期-基期>基期量*10%。从 2011 年开始分析,2011 年
是以2010年作为基期的,问非门票收入,对应柱体灰色部分。验证:2011年:
问同比增速,是和2010年比较,9.46-8.20=1+>8.2*10%=0.8+,满足;2012年:
10.32-9.46=0.8+ < 9.4*10%=0.9+ , 不 满 足 ; 2013 年 : 10.86-10.32=1- <
10.32*10%=1+,不满足;2014年:13.05-10.86=2+>10.86*10%=1+,满足;2015
年:14.58-13.05=1.5+>13.05*10%=1.3+,满足;2016 年:15.61-14.58=1.0+<
14.58*10%=1.4+,不满足;2017年:17.45-15.61=1.8+>15.61*10%=1.5+,满足;
2018年:21.18-17.45=3.0+>17.45*10%=1.7+,满足。共有 2011 年、2014 年、
2015年、2017年、2018年5个年份满足,对应 A项。
方法二:做加法:现期量>基期量*1.1(错位相加)。2011年:基期是2010
年,8.20+0.82=9.0+<9.46,满足;2012 年:9.46+0.946=10.40+>10.32,不满
足;2013 年:10.32+1.032=11+>10.86,不满足;2014 年:10.86+1.086=11+<
13.05 , 满 足 ; 2015 年 : 13.05+1.3=14.3+ < 14.58 , 满 足 ; 2016 年 :
14.58+1.458=15.9+>15.61,不满足;2017年:15.61+1.5≈17.1<17.45,满足;
2018年:17.45+1.745=20-<21.18,满足。共有2011年、2014年、2015年、2017
年、2018年5个年份满足,对应A项。【选A】
常见问法技巧总结
问题:增长率超过10%的有几个?
思路:增长率=(现期-基期)/基期>10%
转化:①现期-基期>基期*10
②现期>基期*1.1(错位相加)
回顾:A*1.1速算技巧——错位相加
1234.5*1.1=
13【注意】常见问法技巧总结:多数据与具体数值比较,先变形化简,再比较。
1.问题:增长率超过10%的有几个?
2.思路:增长率=(现期- 基期)/基期>10%。
3.转化:用加法或者减法,看自己平时做题习惯。
(1)做减法:现期- 基期>基期量*10%。一个数*10%,小数点往前挪一位。
例:9月为24,10月为27.9,11月为29.8,增长率超过10%的月份有几个?
答:10 月:27.9-24=3.9>24*10%=2.4,满足;11 月:29.8-27.9=2-<
27.9*10%=2.79,不满足。
(2)做加法:现期量>基期量*1.1(错位相加)。
①A*1.1速算技巧→错位相加。
②比如1234.5*1.1=1234.5*1+1234.5*0.1=1234.5+123.45=1357.95。
一般增长率
1.基本术语辨析
2.一般增长率计算
3.一般增长率比较
二、比较
一般增长率比较
识别:增长最快/最慢;增速、增幅、增长率最高(大)/最低(小)。
公式:r=增长量/基期量=(现期量-基期量)/基期量=现期量/基期量-1
方法:①当“现期量/基期量”倍数明显,用“现期量/基期量”比较(计算
量小,优先使用)
②当“现期量/基期量”倍数不明显,用“增长量/基期量”比较
14速算:分数比较
【注意】一般增长率比较:
1.识别:增长最快/最慢(生活中一般用快慢形容速度,增长速度谁大谁小,
即增速就是增长率);增速、增幅、增长率最高(大)/最低(小)。
2.公式:r=增长量/基期量=(现期量- 基期量)/基期量=现期量/基期量-1。
题目中很少同时给出增长量和基期量,一般会给出现期量和基期量,比较增长率,
可以简化比较思路。现期量/基期量-1,比较时都“-1”,可以直接比较“现期量
/基期量”。
3.方法:倍数关系是否明显不是绝对判定,而是相对的。
(1)当“现期量/基期量”倍数明显(一般超过2倍),用“现期量/基期量”
比较(计算量小,优先使用)。
(2)当“现期量/基期量”倍数不明显,用“增长量/基期量”比较。
4.速算:分数比较。
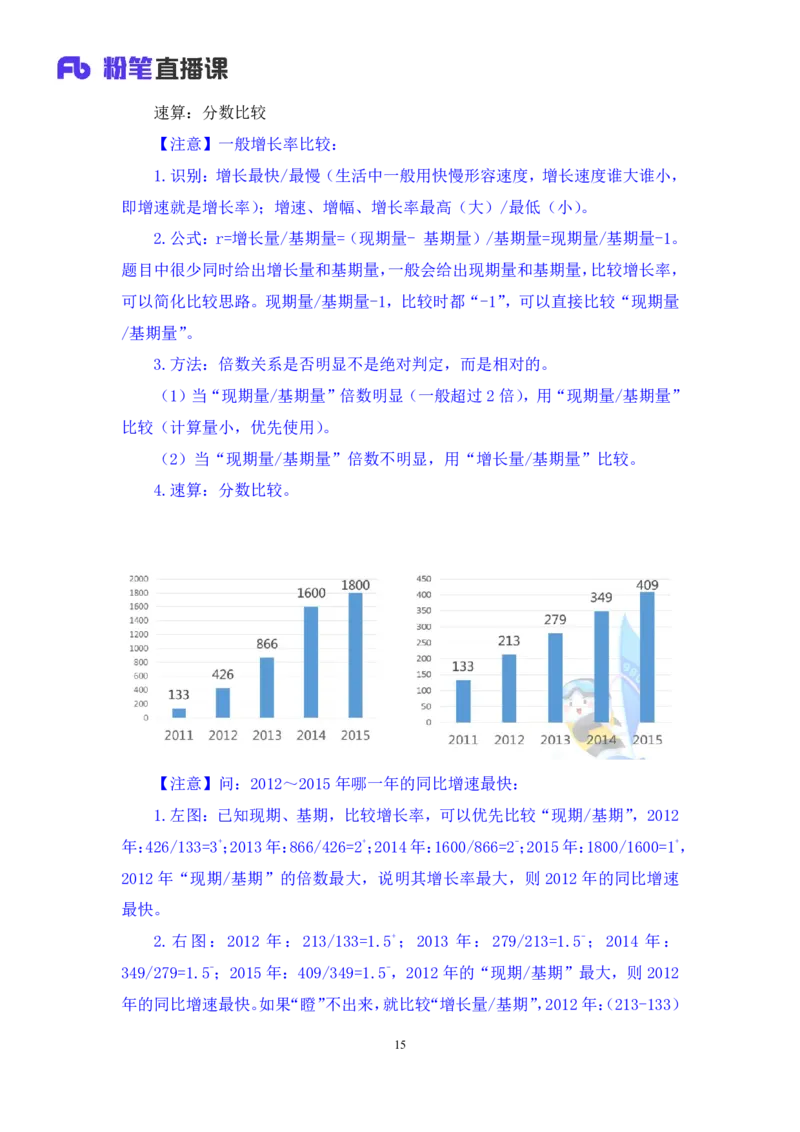
【注意】问:2012~2015年哪一年的同比增速最快:
1.左图:已知现期、基期,比较增长率,可以优先比较“现期/基期”,2012
年:426/133=3+;2013年:866/426=2+;2014年:1600/866=2-;2015年:1800/1600=1+,
2012 年“现期/基期”的倍数最大,说明其增长率最大,则 2012 年的同比增速
最快。
2.右图:2012 年:213/133=1.5+;2013 年:279/213=1.5-;2014 年:
349/279=1.5-;2015年:409/349=1.5-,2012年的“现期/基期”最大,则2012
年的同比增速最快。如果“瞪”不出来,就比较“增长量/基期”,2012年:(213-133)
15/133=80/133;2013年:(279-213)/213=66/213;2014年:(349-279)/279=70/279;
2015 年:(409-349)/349=60/349,四个分数比较,“80/133”的分子最大、分
母最小,即钱多人少分数大,则分数值最大,2012年的同比增速最快。
3.计算能力比较强,可以直接“瞪”,如果计算敏感度不高,可以比较增长
量/基期。
4.很多同学看左图,认为 2014年增速最快,这是因为看了柱子高度差,而
柱子高度差对应的是增长量,无法直接看增长率。
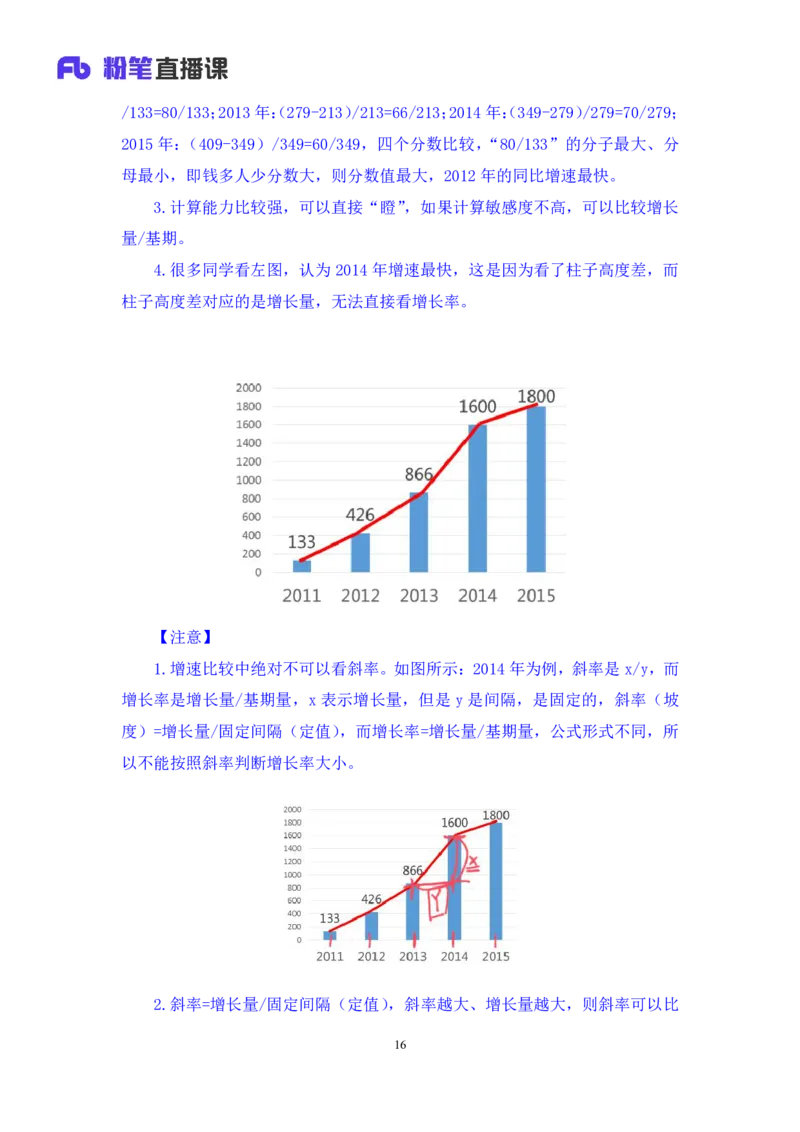
【注意】
1.增速比较中绝对不可以看斜率。如图所示:2014年为例,斜率是x/y,而
增长率是增长量/基期量,x 表示增长量,但是 y 是间隔,是固定的,斜率(坡
度)=增长量/固定间隔(定值),而增长率=增长量/基期量,公式形式不同,所
以不能按照斜率判断增长率大小。
2.斜率=增长量/固定间隔(定值),斜率越大、增长量越大,则斜率可以比
16较增长量,但是没必要,与其比较斜率,不如直接比较高度差(更明显)。
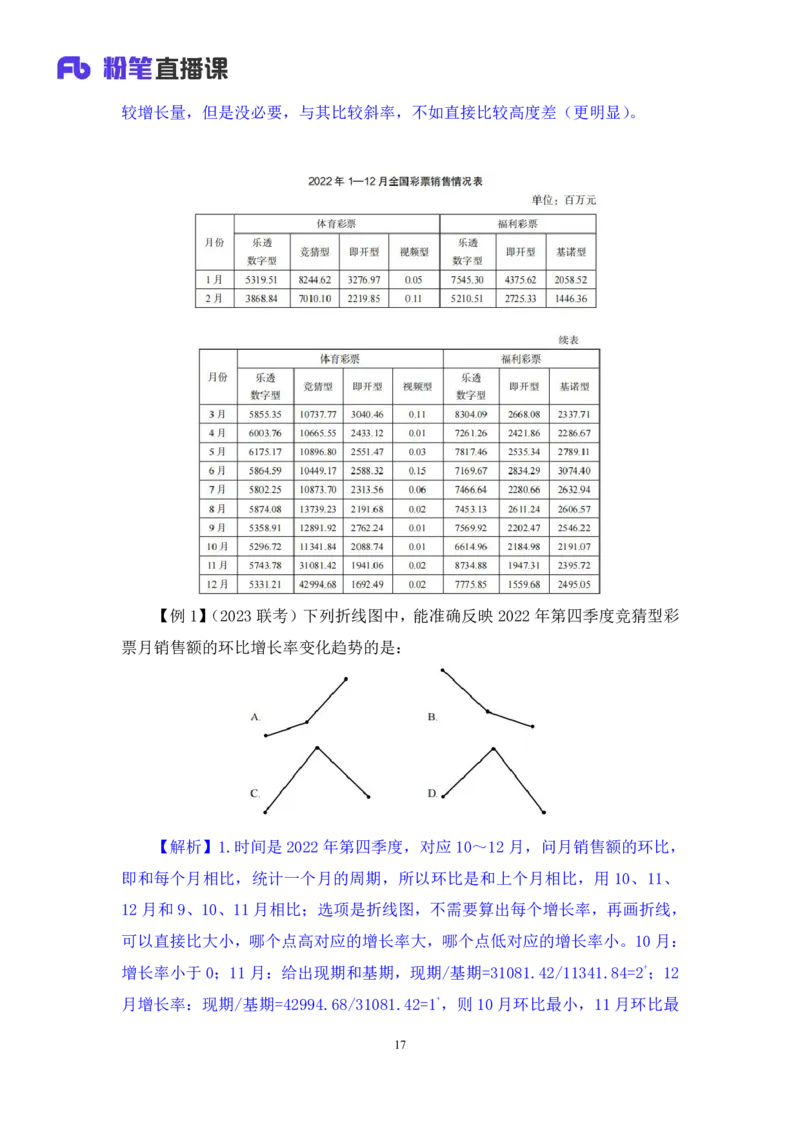
【例1】(2023联考)下列折线图中,能准确反映2022年第四季度竞猜型彩
票月销售额的环比增长率变化趋势的是:
【解析】1.时间是2022年第四季度,对应10~12月,问月销售额的环比,
即和每个月相比,统计一个月的周期,所以环比是和上个月相比,用 10、11、
12月和9、10、11月相比;选项是折线图,不需要算出每个增长率,再画折线,
可以直接比大小,哪个点高对应的增长率大,哪个点低对应的增长率小。10月:
增长率小于0;11月:给出现期和基期,现期/基期=31081.42/11341.84=2+;12
月增长率:现期/基期=42994.68/31081.42=1+,则 10月环比最小,11月环比最
17大,对应C项。【选C】
注:部分数据因四舍五入,存在总计与分项合计不等的情况。
【例2】(2022广东)按不重复距离计算,以下年份中,国际航线里程同比
增速最快的是:
A.2017年 B.2018年
C.2019年 D.2020年
【解析】2.增长率比较问题。时间是2017、2018、2019、2020年,问同比,
是和上一年相比,看现期/基期的倍数,2020年:是负增长,对应的增长率最小,
排除;A、B、C项:现期/基期倍数关系不明显,用增长量/基期,2017年:42/282.8;
2018年:35/324.6;2019年:42/359.9,42/282.8分子大,分母小,对应的分
数大,所以2017年同比增速最快,对应A项。【选A】
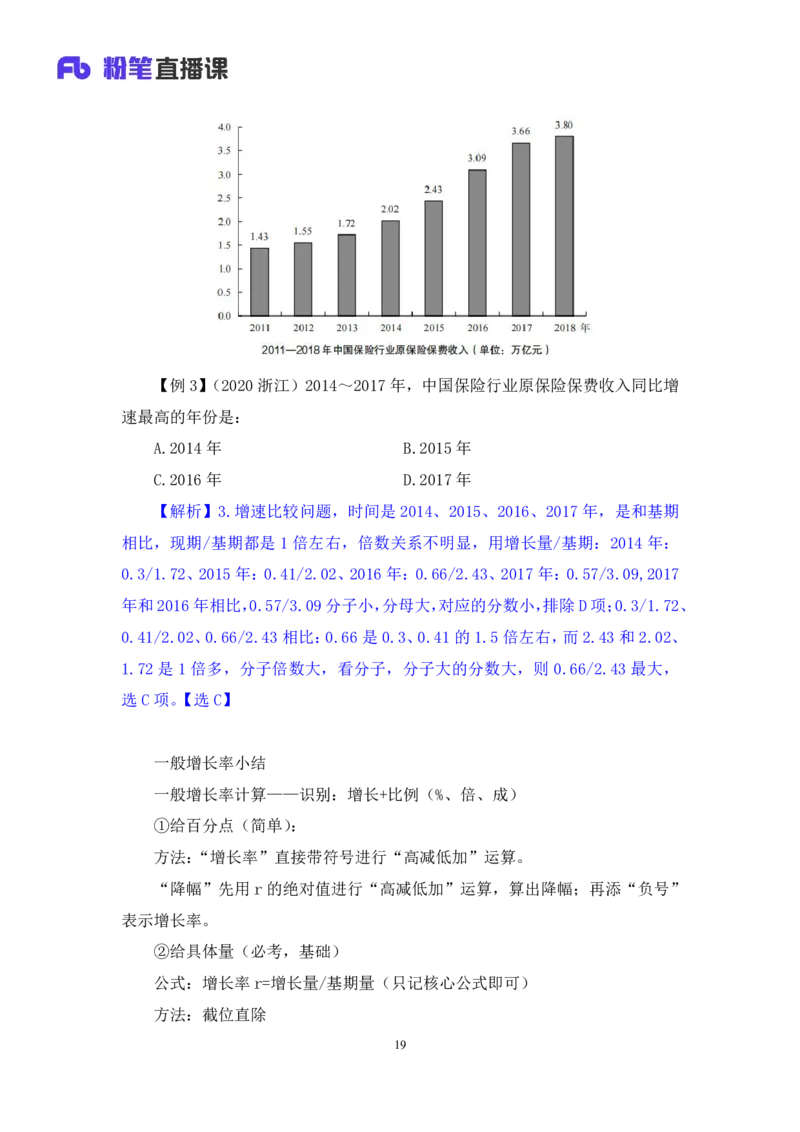
18【例3】(2020浙江)2014~2017年,中国保险行业原保险保费收入同比增
速最高的年份是:
A.2014年 B.2015年
C.2016年 D.2017年
【解析】3.增速比较问题,时间是 2014、2015、2016、2017 年,是和基期
相比,现期/基期都是 1 倍左右,倍数关系不明显,用增长量/基期:2014 年:
0.3/1.72、2015年:0.41/2.02、2016年:0.66/2.43、2017年:0.57/3.09,2017
年和2016年相比,0.57/3.09分子小,分母大,对应的分数小,排除D项;0.3/1.72、
0.41/2.02、0.66/2.43相比:0.66是0.3、0.41的1.5倍左右,而2.43和2.02、
1.72 是 1 倍多,分子倍数大,看分子,分子大的分数大,则 0.66/2.43 最大,
选C项。【选C】
一般增长率小结
一般增长率计算——识别:增长+比例(%、倍、成)
①给百分点(简单):
方法:“增长率”直接带符号进行“高减低加”运算。
“降幅”先用r的绝对值进行“高减低加”运算,算出降幅;再添“负号”
表示增长率。
②给具体量(必考,基础)
公式:增长率r=增长量/基期量(只记核心公式即可)
方法:截位直除
19一般增长率比较——识别:增长最快/慢
①给现期量、基期量(常考,技巧性强)
方法:优先看“现期量/基期量”的倍数,直接比。
无法判定答案,则比较“(现期量- 基期量)/基期量”。
技巧:分数比较
小题型:判断多个年份/主体的增速超过10%
技巧①现期- 基期>基期*10%
技巧②现期>基期*1.1
【注意】一般增长率小结:
1.一般增长率计算——识别:增长+比例(%、倍、成)。
(1)给百分点(简单):
①方法:
a.“增长率”直接带符号进行“高减低加”运算。
b.“降幅”先用r的绝对值进行“高减低加”运算,算出降幅;再添“负号”
表示增长率。
(2)给具体量(必考,基础):
①计算公式:增长率r=增长量/基期量,只记住核心公式即可。
②方法:截位直除。
2.一般增长率比较——识别:增长最快/慢(速度描述)。
(1)给现期量、基期量(常考,技巧性强)。
(2)方法:分数比较。
①优先看“现期量/基期量”的倍数,直接比。
②无法判定答案,则比较“(现期量- 基期量)/基期量”。
(3)小题型:判断多个年份/主体的增速超过10%。先变型、再比较。
①技巧一:现期- 基期>基期*10%。
②技巧二:现期>基期*1.1(错位相加)。
20第四节 增长量
增长量是用来表述现期量与基期量变化的绝对量
1.增长量计算类
2.增长量比较类
【注意】增长量:用来表述现期量与基期量变化的绝对量,即现期量与基期
量的差值。
1.增长量计算类。
2.增长量比较类。
一、计算
增长量计算类
识别:增长+具体单位
①已知现期量、基期量
公式:增长量=现期量- 基期量
例:2018年小跑的体重为8斤,2022年为10斤。与2018年相比,2022年
小跑的体重增长了多少斤?
【注意】增长量计算类:
1.识别:增长+具体单位(比如元/人/斤)。对比:上升/下降+%,考查增长
率的计算。
2.已知现期量、基期量:
(1)公式:增长量=现期量- 基期量。
21(2)例:2018年小跑的体重为8斤,2022 年为10斤。与2018年相比,2022
年小跑的体重增长了多少斤?
答:增长+单位,求增长量,增长量=10-8=2斤。
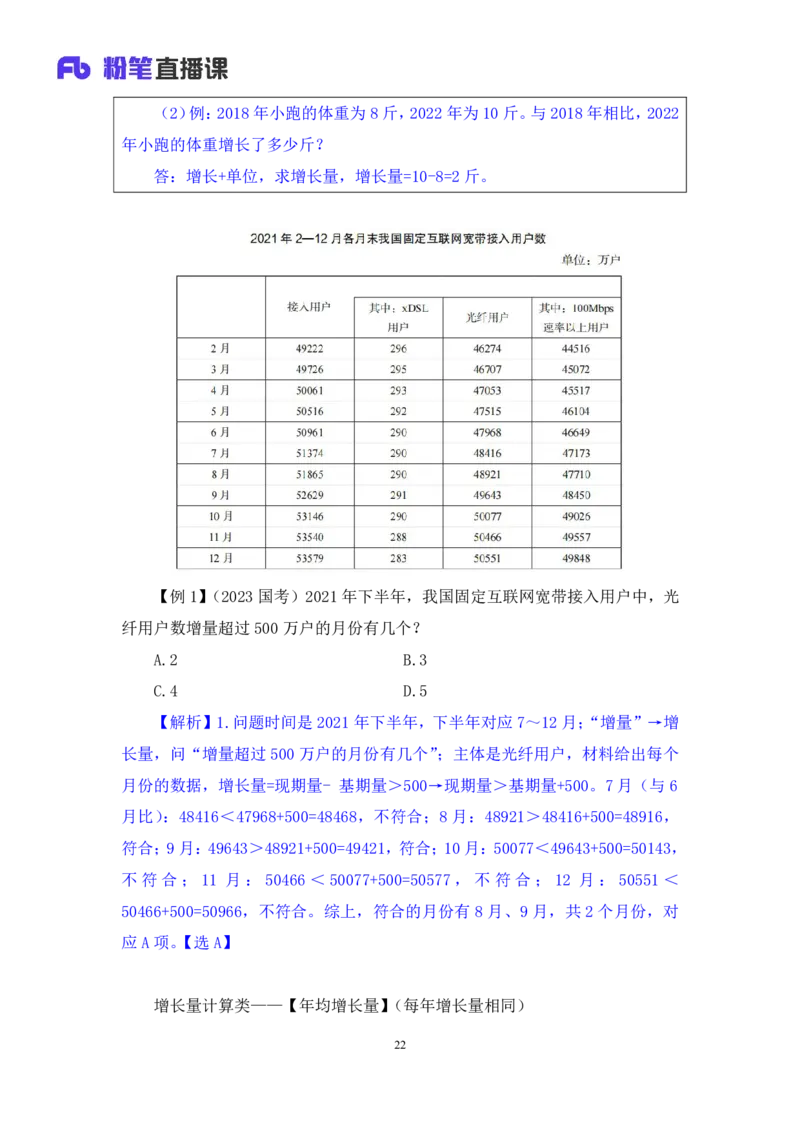
【例1】(2023国考)2021年下半年,我国固定互联网宽带接入用户中,光
纤用户数增量超过500万户的月份有几个?
A.2 B.3
C.4 D.5
【解析】1.问题时间是2021年下半年,下半年对应7~12月;“增量”→增
长量,问“增量超过 500万户的月份有几个”;主体是光纤用户,材料给出每个
月份的数据,增长量=现期量- 基期量>500→现期量>基期量+500。7月(与6
月比):48416<47968+500=48468,不符合;8 月:48921>48416+500=48916,
符合;9 月:49643>48921+500=49421,符合;10月:50077<49643+500=50143,
不符合;11 月: 50466<50077+500=50577,不符合; 12 月:50551<
50466+500=50966,不符合。综上,符合的月份有 8 月、9 月,共 2 个月份,对
应A项。【选A】
增长量计算类——【年均增长量】(每年增长量相同)
22识别:年均(平均每年)+增长+具体单位
①已知现期量、基期量,公式:年均增长量=(现期量- 基期量)/年份差N
例:2018年小跑的体重为 8 斤,2022 年为 10斤。2018年~2022 年小跑的
体重平均每年增长了多少斤?
【注意】增长量计算类——年均增长量(假设每年增长量相同):
1.识别:年均(平均每年)+增长+具体单位。
2.已知现期量、基期量:
(1)公式:年均增长量=(现期量- 基期量)/年份差N。
(2)例:2018年小跑的体重为8斤,2022年为10斤。2018~2022年小跑
的体重平均每年增长了多少斤?
答:假设平均每年增长 a 斤,一共增长了 4 个a,即 8+4a=10→a=(10-8)
/4=0.5;a 是年均增长量,10 是现期(时间靠后的数据)、8 是基期(时间靠前
的数据),4是增长的次数(年份差)→2022-2018=4。
年均增长问题——年份差N 的确定
年份差N=现期时间- 基期时间(没有差异)
一般情况(包括浙江、国考),2016年~2020年:两个时间直接相减
现期:2020年,基期:2016年→年份差N:4
五年规划(全国都一样),十三五期间(2016年~2020年):年份差为5
现期:2020年,年份差N:5→基期:2015年
江苏省考,2016年~2020年:基期往前推一年
现期:2020年,基期:2015年→年份差N:5
时间段以2016年~2020年为例:
23注:
1.江苏省考或出现“五年规划”描述,基期往前推一年
2.浙江省考、国考属于一般情况,基期不前推
【注意】年均增长问题——年份差 N 的确定:年份差 N=现期时间- 基期时
间(没有差异)。
1.一般情况(常规考法,包括浙江、国考):给出时间段,没有特殊描述,
默认时间靠后的是现期、时间靠前的是基期。2016~2020年:现期→2020年,
基期→2016年,两个时间直接相减→年份差N:4。
2.五年规划(全国都一样):“十三五”期间(2016~2020年),“五”→年
份差(N)为5。现期:2020 年;如果基期为 2016 年,2020-2016=4,则基期往
前推一年→基期为2015 年。理解:“十三五”讨论五年的数据变化,和“十二
五”相比,“十三五”的期末 2020 年与“十二五”的期末 2015年进行比较,则
年份差为5。拓展:“十四五”为 2021年~2025年,目前还没有结束,大概率不
会出现“十四五”的数据;现阶段,重点掌握“十三五”、“十二五”即可。
3.江苏省考(了解即可):默认基期往前推一年。2016~2020年:现期→2020
年,基期→2015年,年份差N为 5。
4.时间段以2016~2020年为例:
5.注:
(1)江苏省考或出现“五年规划”描述,基期往前推一年。
(2)浙江省考、国考属于一般情况,基期不前推。
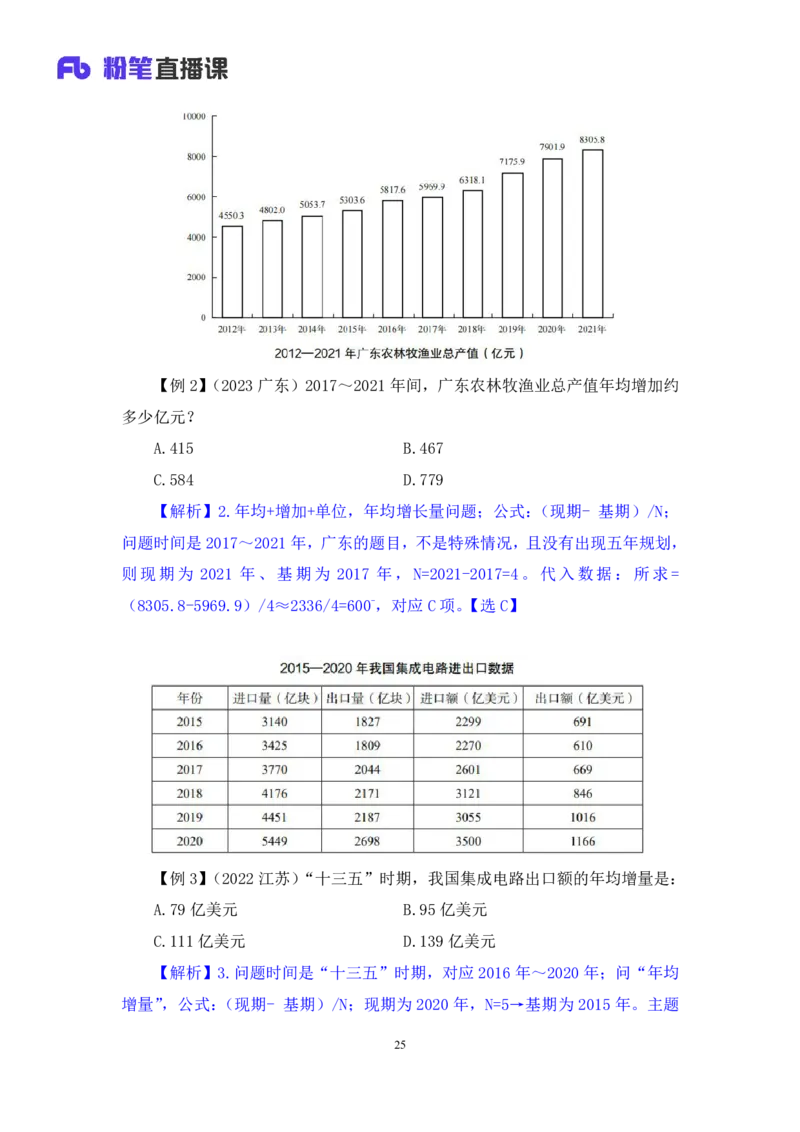
24【例2】(2023广东)2017~2021年间,广东农林牧渔业总产值年均增加约
多少亿元?
A.415 B.467
C.584 D.779
【解析】2.年均+增加+单位,年均增长量问题;公式:(现期- 基期)/N;
问题时间是2017~2021年,广东的题目,不是特殊情况,且没有出现五年规划,
则现期为 2021 年、基期为 2017 年,N=2021-2017=4。代入数据:所求=
(8305.8-5969.9)/4≈2336/4=600-,对应C项。【选C】
【例3】(2022江苏)“十三五”时期,我国集成电路出口额的年均增量是:
A.79亿美元 B.95亿美元
C.111亿美元 D.139亿美元
【解析】3.问题时间是“十三五”时期,对应2016年~2020年;问“年均
增量”,公式:(现期- 基期)/N;现期为 2020 年,N=5→基期为 2015 年。主题
25词是“集成电路出口额”,所求=(1166-691)/5=400+/5=80+,排除A项;结果到
不了100,排除C、D项,选择B项。【选B】
增长量计算类
识别:增长+具体单位
②已知现期量、增长率r
【补例 1】2022 年小跑的体重为 10 斤,比 2018 年增长 25%。求:与 2018
年相比,2022年小跑的体重增长了多少斤?
公式推导其实不重要:r=增长量/基期量→增长量=基期量*r=现期量/(1+r)
*r。
速算:
①增长率百化分,|r|=1/n
②增长量=现期量/(n+1)
【注意】增长量计算类:
1.识别:增长+具体单位。
2.已知现期量、增长率r(重点):
(1)公式:增长量=现期量/(1+r)*r。
(2)公式推导(其实不重要):r=增长量/基期量→增长量=基期量*r=现期
量/(1+r)*r。
(3)补例:2022年小跑的体重为10斤,比2018年增长25%。求:与2018
年相比,2022年小跑的体重增长了多少斤?
答:可以利用“增长量=现期量- 基期量”计算,所求=10-10/(1+25%)=10-8=2;
但是,考试时的数据不整,则算得慢。或者利用“增长量=现期量/(1+r)*r”
计算,所求=10/(1+25%)*25%,仍然不好计算。考虑百化分,r=25%=1/4→n=4,
增长量=现期/(n+1)=10/(4+1)=10/5=2。
3.速算:
(1)增长率百化分,|r|=1/n。
(2)r>0,增长量=现期量/(n+1)。
(3)原理(不重要):r=1/n,增长量=现期量/(1+r)*r→增长量=现期÷
26(1+1/n)*(1/n)=现期÷[(n+1)/n]*(1/n)=现期/(n+1)。
【注意】百化分记忆:
1.不用背,我也会:50%=1/2,33.3%≈1/3,25%=1/4,20%=1/5,10%=1/10。
2.互为倒数,成对记忆(6&16、7&14、8&12、9&11):6.25%=1/16、16.7%
≈1/6;7.1%≈1/14、14.3%≈1/7;8.3%≈1/12、12.5%=1/8;9.1%≈1/11、11.1%
≈1/9。原理:9*11=99≈100,即9/100≈1/11、11/100≈1/9。
3.等差数列(5.0→3→6→9,20→19→18→17):5.0%=1/20,5.3%≈1/19,
5.6%≈1/18,5.9%≈1/17。
274.77老师腿长1米3(66同学身高 1米5):7.7%≈1/13,6.6%≈1/15。
国家能源局发布2022年1~7月,全社会用电量累计49303亿千瓦时,同比
增长3.4%。分产业看,第一产业用电量634亿千瓦时,同比增长11.1%;第二产
业用电量32552亿千瓦时,同比增长1.1%;第三产业用电量8531亿千瓦时,同
比增长 4.6%;城乡居民生活用电量 7586 亿千瓦时,同比增长 12.5%。7 月份,
全社会用电量8324亿千瓦时,同比增长 6.3%。分产业看,第一产业用电量121
亿千瓦时,同比增长 14.3%;第二产业用电量 5132亿千瓦时,同比下降 0.1%;
第三产业用电量1591亿千瓦时,同比增长11.5%;城乡居民生活用电量1480亿
千瓦时,同比增长26.8%。
【例4】(2023联考)2022年 1~7月份,全国城乡居民生活用电量比2021
年1~7月份约多:
A.672亿千瓦时 B.843亿千瓦时
C.925亿千瓦时 D.1020亿千瓦时
【解析】4.多+单位(亿千瓦时),增长量问题。主题词是“城乡居民生活用
电量”,已知“城乡居民生活用电量7586亿千瓦时,同比增长12.5%”。r=12.5%=1/8,
增长量=现期/(n+1)=7586/(8+1)=7586/9,首位商8,对应B项。【选B】
2020年全国人口共141178万人,比2010年增长了约5.38%。从地区分布上
看,2020年东部地区人口占39.93%,中部地区占25.83%,西部地区占27.12%,
东北地区占6.98%。与2010年相比,东部地区人口所占比重上升2.15个百分点,
中部地区下降0.79个百分点,西部地区上升 0.22个百分点,东北地区下降1.20
个百分点。
【例 5】(2022 联考)2020 年全国人口比 2010 年全国人口增加的数量位于
以下哪个区间?
A.5000万~6000万人 B.6000万~7000万人
C.7000万~8000万人 D.8000万~9000万人
【解析】5.增加的数量+单位,增长量问题。主题词是全国人口,已知“2020
年全国人口共 141178 万人,比 2010 年增长了约 5.38%”;5.0%=1/20→5.38%≈
281/19,增长量=现期/(n+1)≈141178/(19+1)=141178/20,首位商7+,对应C
项。【选C】
【注意】如果将“n”看成20,141178/21→首位商7-,则会错选B项。
增长率百化分之倒数法(适用20%以内整数)
利用与背过的百分数的倒数关系,实现百化分
a*b=100,1/a=b%→a%=1/b
练习:
4%≈
15%≈
增长率百化分之放缩法(适用较大或较小数字)
利用与背过的百分数的倍数关系,实现百化分
练习:
3.3%≈
77%≈
22%≈
增长率百化分之取中法※※※
如果遇到百分数左右难取舍,且选项接近,取中间值即可
练习:
22%≈
18.4%≈
增长率百化分之公式法(浪费时间,慎用)
如果遇到百分数实在想不起来
硬除:n=100/百分号前的数字(保留小数点后一位)
练习:7.1%≈
【注意】百化分技巧:
1.增长率百化分之倒数法(适用20%以内整数):
(1)利用与背过的百分数的倒数关系,实现百化分。a*b=100,1/a=b%→
29a%=1/b。
(2)练习:
①4%:1/4=25%,4*25=100→4%=1/25。
②15%:1/15≈6.6%,则15%≈1/6.6。
2.增长率百化分之放缩法(适用较大或较小数字):
(1)利用与背过的百分数的倍数关系,实现百化分。
(2)练习:
①3.3%:33%≈1/3,则3.3%=1/10*33%≈1/3*(1/10)=1/30。
②77%:7.7%≈1/13,则77%=10*7.7%≈10*(1/13)=10/13=1/1.3。
③22%:11%≈1/9,则22%=2*11%≈1/9*2=2/9=1/4.5。
3.增长率百化分之取中法(用得最多):
(1)如果遇到百分数左右难取舍,且选项接近,取中间值即可。
(2)练习:
①22%:22%介于25%(1/4)与 20%(1/5)之间,则22%≈1/4.5。
②18.4%:18.4%介于20%(1/5)与16.7%(1/6)之间,则18.4%≈1/5.5。
4.增长率百化分之公式法(兜底的方法,需要动笔计算→浪费时间,慎用):
(1)如果遇到百分数实在想不起来,硬除:n=100/百分号前的数字(保留
小数点后一位)。
(2)练习:比如7.1%,100/7.1≈14.0,则7.1%≈1/14.0。
5.练习:利用微信小程序“粉笔快练”,数资速算→百分数与分数、首位计
算、尾数计算。
302023年4月份,我国社会消费品零售总额34910亿元,同比增长18.4%。其
中,除汽车以外的消费品零售额31290亿元,增长16.5%。
【例6】(2023河北事业单位)2023年4月,我国社会消费品零售总额同比
增加:
A.4678亿元 B.5425亿元
C.6414亿元 D.7212亿元
【解析】6.问题时间是2023年4月,与材料时间一致;增加+单位,增长量
问题。定位材料找数据,r=18.4%,介于 20%(1/5)与 16.7%(1/6)之间,则
18.4%≈1/5.5;增长量=现期量/(n+1)≈34910/(5.5+1)=34910/6.5,首位商
5+,对应B项。【选B】
2019年6月,全国发行地方政府债券8996亿元,同比增长68.37%,环比增
长195.63%。其中,发行一般债券3178亿元,同比减少28.33%,环比增长117.08%,
发行专项债券5818亿元,同比增长 540.04%,环比增长268.46%;按用途划分,
发行新增债券7170亿元,同比增长127.11%,环比增长332.71%,发行置换债券
和再融资债券1826亿元,同比减少 16.47%,环比增长31.75%。
【例 7】(2020 联考)2019 年 6 月,全国发行的地方政府债券比 2018 年 6
月多约:
A.6151亿元 B.5953亿元
C.3653亿元 D.3043亿元
【解析】7.问题时间是2019 年6月,与材料时间一致;问“多多少亿元”,
增长量问题;主体为“地方政府债券”,给出现期和 r,考虑百化分。
r=68.37%≈66%=10*6.6%≈10*(1/15)=10/15=1/1.5,或者68.37%≈66%=2*33%
≈2/3=1/1.5;增长量≈8996/(1.5+1)=8996/2.5。
方法一:直接计算。首位商3、次位商6,对应C项。
方法二:8996/2.5≈9000*(1/2.5)=9000*0.4,或者不看量级,有效数字
→9*4=36,对应C项。【选C】
31【注意】同比看头、环比看尾,本题是2019年6月与2018年6月相比→用
年做比较→同比;如果是2019年 6月与2019年5月相比,则为环比。
增长量计算类
识别:增长+具体单位
②已知现期量、增长率r
公式:增长量=现期量/(1+r)*r
速算:
①增长率百化分,|r|=1/n
②r>0,增长量=现期量/(n+1)
易错点注意:若r<0,则增长量=-现期量/(n-1)
【补例2】2023年小跑的体重为9斤,同比下降10%。求:2023年小跑的体
重减少了多少斤?
【注意】增长量计算类:
1.识别:增长+具体单位。
2.已知现期量、增长率r:
(1)公式:增长量=现期量/(1+r)*r。
(2)速算:
①增长率百化分,|r|=1/n。
②r>0,增长量=现期量/(n+1)。
③易错点注意:若r<0,则增长量=-现期量/(n-1),记忆→减少量=现期/
(n-1)。
3.补例:2023 年小跑的体重为 9 斤,同比下降 10%。求:2023 年小跑的体
重减少了多少斤?
答:下降10%→r=-10%,则|r|=|-10%|=1/10,减少量=9/(10-1)=1。
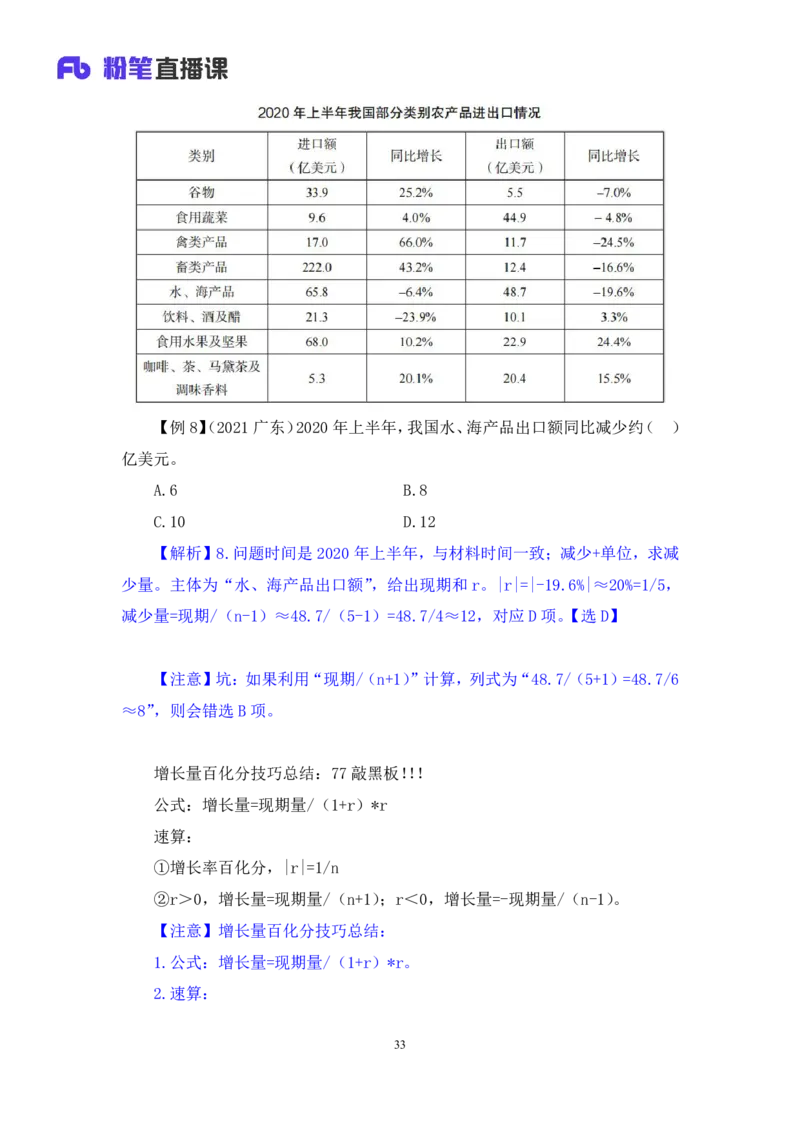
32【例8】(2021广东)2020年上半年,我国水、海产品出口额同比减少约( )
亿美元。
A.6 B.8
C.10 D.12
【解析】8.问题时间是2020年上半年,与材料时间一致;减少+单位,求减
少量。主体为“水、海产品出口额”,给出现期和r。|r|=|-19.6%|≈20%=1/5,
减少量=现期/(n-1)≈48.7/(5-1)=48.7/4≈12,对应D项。【选D】
【注意】坑:如果利用“现期/(n+1)”计算,列式为“48.7/(5+1)=48.7/6
≈8”,则会错选B项。
增长量百化分技巧总结:77 敲黑板!!!
公式:增长量=现期量/(1+r)*r
速算:
①增长率百化分,|r|=1/n
②r>0,增长量=现期量/(n+1);r<0,增长量=-现期量/(n-1)。
【注意】增长量百化分技巧总结:
1.公式:增长量=现期量/(1+r)*r。
2.速算:
33(1)增长率百化分,|r|=1/n。
(2)r>0,增长量=现期量/(n+1);r<0,增长量=-现期量/(n-1)。
(3)记忆:|r|=1/n,r>0→现期量/(n+1),r<0→现期量/(n-1)。
二、比较
增长量比较
识别:增长+多/少(增长最多/最少、下降最多/最少)
题型:
①已知现期量和基期量
②已知现期量和增长率r
【注意】增长量比较:
1.识别:增长+多/少(增长最多/最少、下降最多/最少)。对比:增长+快/
慢,增长率比较。
2.题型:
(1)已知现期量和基期量。
(2)已知现期量和增长率r。
增长量比较:
识别:增长+多/少(增长最多/最少、下降最多/最少)
①已知现期量、基期量:增长量=现期量- 基期量
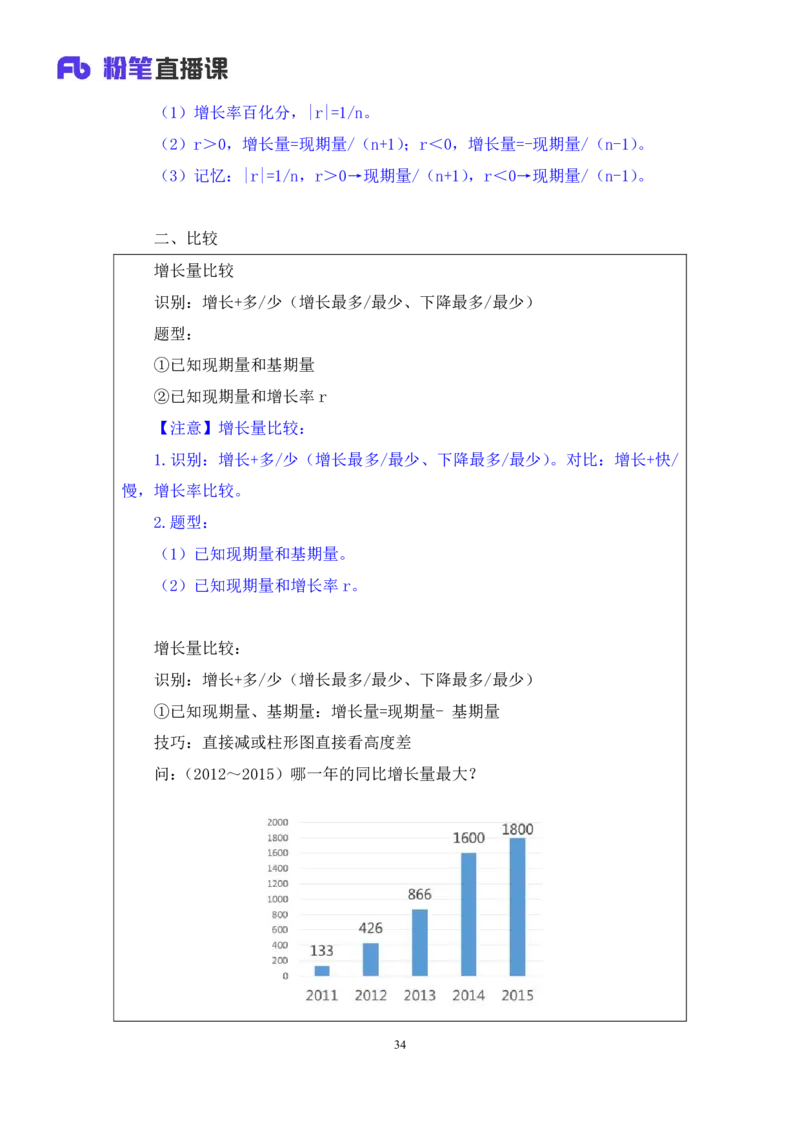
技巧:直接减或柱形图直接看高度差
问:(2012~2015)哪一年的同比增长量最大?
34A.2012 B.2013
C.2014 D.2015
【注意】增长量比较:
1.识别:增长+多/少(增长最多/最少、下降最多/最少)。
2.题型:
(1)已知现期量、基期量:增长量=现期量- 基期量。
①技巧:直接减或柱形图直接看高度差(高度差代表增长量的大小关系)。
②问:(2012~2015)哪一年的同比增长量最大?
A.2012 B.2013
C.2014 D.2015
答:材料给出柱状图,直接看高度差,2014年的高度差最大,选择C项。
(2)已知现期量和增长率r。
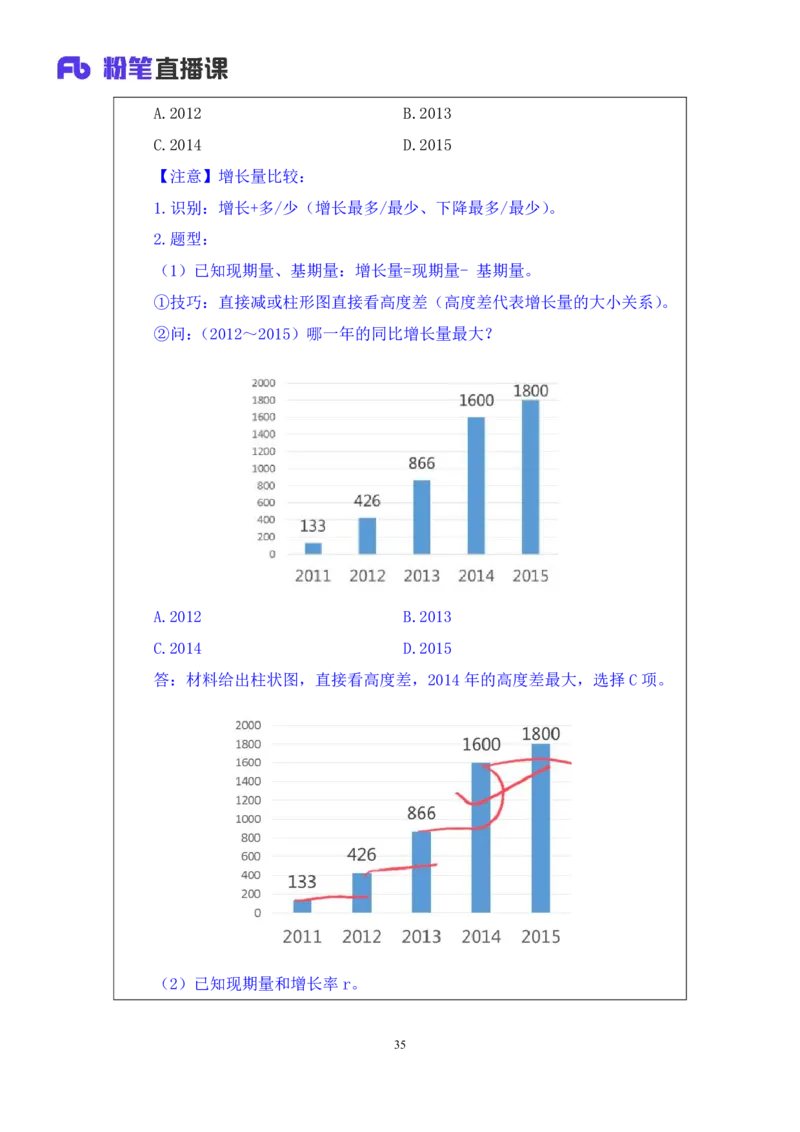
35【拓展】(2015山东)以下几个年份中,国有建设用地供应面积同比增量最
多的年份是:
A.2010 B.2011
C.2012 D.2013
【解析】拓展.“国有建设用地”对应标题,即四个部分相加为国有建设用
地。直接计算比较麻烦,四个数据相加就是柱子的总高度,则可以看高度差;2011
年的高度差最大,选择B项。【选B】
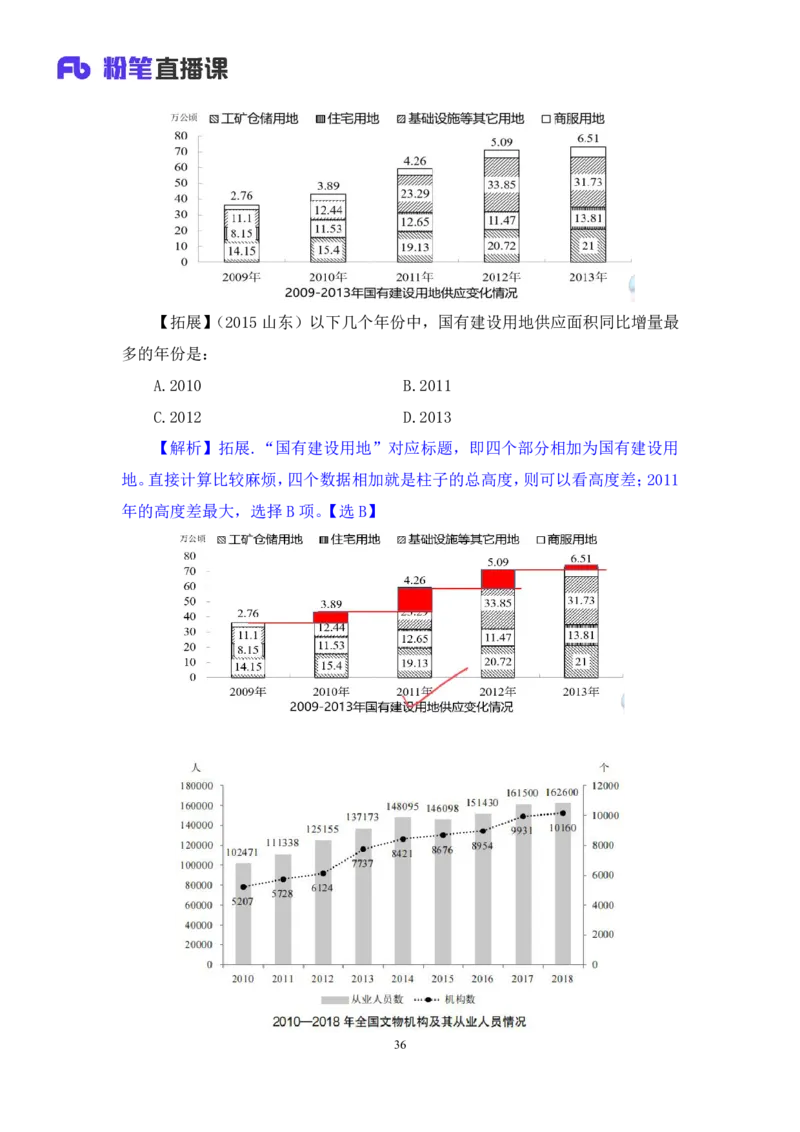
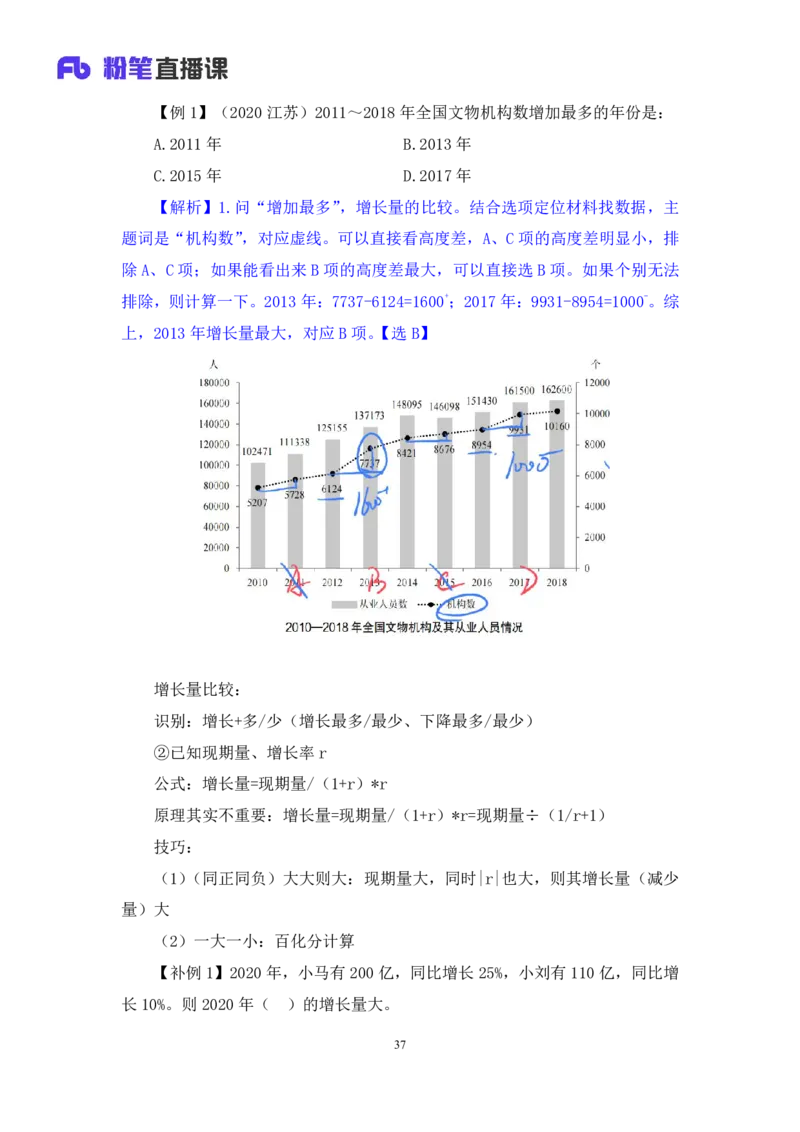
36【例1】(2020江苏)2011~2018年全国文物机构数增加最多的年份是:
A.2011年 B.2013年
C.2015年 D.2017年
【解析】1.问“增加最多”,增长量的比较。结合选项定位材料找数据,主
题词是“机构数”,对应虚线。可以直接看高度差,A、C项的高度差明显小,排
除A、C项;如果能看出来 B项的高度差最大,可以直接选 B项。如果个别无法
排除,则计算一下。2013年:7737-6124=1600+;2017年:9931-8954=1000-。综
上,2013年增长量最大,对应B 项。【选B】
增长量比较:
识别:增长+多/少(增长最多/最少、下降最多/最少)
②已知现期量、增长率r
公式:增长量=现期量/(1+r)*r
原理其实不重要:增长量=现期量/(1+r)*r=现期量÷(1/r+1)
技巧:
(1)(同正同负)大大则大:现期量大,同时|r|也大,则其增长量(减少
量)大
(2)一大一小:百化分计算
【补例1】2020年,小马有200亿,同比增长 25%,小刘有110亿,同比增
长10%。则2020年( )的增长量大。
37【补例2】2020年,小马有200亿,同比下降 25%,小刘有110亿,同比下
降10%。则2020年( )的减少量大。
【补例3】2020年,小马有 200亿,同比增长25%,小刘有110亿,同比增
长50%。则2020年( )的增长量大。
【补例4】2020年,小马有200亿,同比增长10%,小刘有200亿,同比减
少10%。则2020年( )的增长量大。( )的变化量大。
【注意】增长量比较:
1.识别:增长+多/少(增长最多/最少、下降最多/最少)。
2.已知现期量、增长率r:
(1)公式:增长量=现期量/(1+r)*r。
(2)技巧:
①(同正同负)大大则大:现期量大,同时|r|也大,则其增长量/减少量大。
a.原理其实不重要:增长量=现期量/(1+r)*r=现期量÷(1/r+1),r变大
→1/r变小→分母变小→分数值(增长量)变大。
b.补例1:2020年,小马有200亿,同比增长25%,小刘有110亿,同比增
长10%。则2020年( )的增长量大。
答:小马的现期大(200>110)、增长率大(25%>10%),大大则大,则小马
的增长量大。
c.补例2:2020年,小马有 200亿,同比下降25%,小刘有110亿,同比下
降10%。则2020年( )的减少量大。
答:增长率同负,小马的现期大(200>110)、降幅大(|-25%|>|-10%|),
大大则大,则小马的减少量大。
②一大一小:稳妥起见→百化分计算。
a.补例3:2020年,小马有 200亿,同比增长25%,小刘有110亿,同比增
长50%。则2020年( )的增长量大。
答:如果利用“现期量*r”计算,200*25%=50、110*50%=55,小刘的增长量
大,则是错误的。利用百化分计算,小马:25%=1/4,增长量=200/(4+1)=40;
小刘:50%=1/2,增长量=110/(2+1)=40-;综上,小马的增长量大。解释:增
长量=现期量/(1+r)*r,只计算“现期量*r”时,则忽略了“1+r”;现阶段,
38稳妥起见,建议利用完整的公式“现期量/(1+r)*r”进行分析。
b.补例4:2020年,小马有200亿,同比增长10%,小刘有200亿,同比减
少10%。则2020年( )的增长量大。( )的变化量大。
答:如果比较增长量,增长量可正可负,正的>负的→小马的增长量>小刘
的增长量。如果比较变化量,变化量可正可负,比较看绝对值;10%=1/10,小马
变化量=200/(10+1)<小刘变化量=200/(10-1),小刘的变化量大。解释:现
期量、|r|虽然是一样,但是基期不一样;小马基期小于 200→在不到 200 的数
上增长量 10%→增长量<20,小刘的基期大于 200→在大于 200 的数上减少 10%
→减少量>20,则二者的变化量不一样。
2018年木家具进口金额9.24 亿美元,增长3.6%,木框架坐具进口金额3.32
亿美元,增长 13.8%。刨花板 2016 年进口增幅 41%,2017 年增幅 21%,2018 年
进口 69.2 万吨,为负增长(-2.7%)。2018 年木制品出口金额仅增长 2%。2018
年木家具出口数量增长5.68%,金额负增长1.6%,木地板出口26.6万吨,3.85
亿美元,分别下降24.8%和下降25.9%。胶合板出口1137.8万立方米,55.56亿
美元,数量增长 5%,金额增长 9%,纤维板出口 179 万吨,38.35 亿美元,数量
下降 14.9%,金额增长 6.2%。木制品出口企业普遍效益下降。2018 年进口针叶
原木4159.7万立方米,金额57.86亿美元,同比分别增长8.8%和12.6%。
【例2】(2021新疆兵团)2018 年,下列三种产品出口金额增长值从大到小
的顺序排列正确的是:
A.木地板、胶合板、纤维板 B.胶合板、纤维板、木地板
C.木地板、纤维板、胶合板 D.胶合板、木地板、纤维板
【解析】2.问题时间是2018年,与材料时间一致,“增长值从大到小的顺序
排列”→增长量比较问题;定位材料找“金额”数据,木地板的增长率为负,纤
维板、胶合板的增长率为正,正的>负的,则木地板排在最后;结合选项,对应
B项。【选B】
按收入来源分,(2019年)前三季度,全国居民人均工资性收入13020元,
增长8.6%;人均经营净收入 3757 元,增长 9.3%;人均财产净收入 1949元,增
39长12.3%;人均转移净收入4157 元,增长7.2%。
【例3】(2021新疆兵团)2019年前三季度,四种收入来源中收入同比增量
最高的是:
A.人均工资性收入 B.人均经营净收入
C.人均财产净收入 D.人均转移净收入
【解析】3.问题时间是2019年前三季度,与材料时间一致,“同比增量最高”
→增长量比较问题。定位材料找数据,A、D项比较:A 项的现期量大(13020>
4157)、r 大(8.6%>7.2%),大大则大,A 项>D 项,排除 D 项。接下来考虑百
化分计算,A 项:8.6%≈1/12,增长量≈13020/13=1000+;B 项;9.3%≈1/11,
增长量≈3757/12=1000-;C项:12.3%≈1/8,增长量≈1949/9=1000-。综上,选
择A项。【选A】
2018年前三季度,S省物流相关行业实现总收入1912.8亿元,同比增长6.6%。
其中:运输环节收入1321.9亿元,同比增长6.0%;保管环节收入226.2亿元,
同比增长 6.4%;邮政业收入 82.8亿元,同比增长 16.7%;配送、加工、包装业
收入98.8 亿元,同比增长6.4%。
【例 4】(2020国考)将2018 年前三季度S省物流相关行业不同类型的收入
按照同比增量从高到低排列,以下正确的是:
A.运输收入>保管收入>邮政业收入>配送、加工、包装业收入
B.运输收入>配送、加工、包装业收入>邮政业收入>保管收入
C.运输收入>保管收入>配送、加工、包装业收入>邮政业收入
D.运输收入>邮政业收入>配送、加工、包装业收入>保管收入
【解析】4.问题时间是2018年前三季度,与材料时间一致;“同比增量从高
到低排列”→排序题,资料分析→选项为王。结合选项,发现运输收入都是排第
一,则不用比较。比较保管和配送:保管和配送增长率(6.4%)相同,保管现期
226.2>配送现期98.8,保管增长量>配送增长量,排除B、D项。剩余A、C项,
比较邮政和配送即可。
方法一:后期可以直接“瞪”。邮政:现期为 82.8、r 为 16.7%;配送:现
期为98.8、r为6.4%。现期很接近,r差距比较大,则r大的增长量大,邮政增
40长量>配送增长量,对应A项。
方法二:百化分。邮政:16.7%≈1/6,增长量≈82.8/(6+1)>10;配送:
6.4%≈1/16,增长量≈98.8/(16+1)<10;邮政增长量>配送增长量,对应 A
项。【选A】
增长量小结
增长量计算——识别:(年均)增长+具体单位
(1)已知现期量、基期量,公式:增长量=现期量- 基期量;年均增长量=
(现期量- 基期量)/年份差N。
(2)已知现期量、增长率r
方法:
①|r|=1/n
②r>0,增长量=现期量/(n+1);r<0,增长量=-现期量/(n-1)(少,容
易忽视)
增长量比较——识别:增长+多/少
(1)已知现期量、基期量(简单,考得少):
公式:增长量=现期量- 基期量
方法:减法,柱形图可看高度差
(2)已知现期量、增长率r
方法:
①同正同负,大大则大:r同号,现期值大,|r|也大,则其增长量/减少量
大
②其他情况,百化分
41【注意】增长量小结:
1.增长量计算——识别:(年均)增长+具体单位。
(1)已知现期量、基期量,公式:增长量=现期量- 基期量;年均增长量=
(现期量- 基期量)/年份差N。
(2)已知现期量、增长率r——方法:
①|r|=1/n,n为分母。
②r>0,增长量=现期量/(n+1);r<0,增长量=-现期量/(n-1)(少,容
易忽视)。
2.增长量比较——识别:增长+多/少。对比:增长+快/慢,增长率比较。
(1)已知现期量、基期量(简单,考得少):
①公式:增长量=现期量- 基期量。
②方法:减法,柱形图可看高度差。
(2)已知现期量、增长率r——方法:
①同正同负,大大则大:r同号,现期值大,|r|也大,则其增长量/减少量
大。
②其他情况,稳妥起见→百化分。
【练习1】(2018浙江)2016年该市上划中央收入同比约增长了:
A.37% B.44%
C.51% D.58%
【解析】练习1.课堂正确率为60%。增长+%,求增长率。主体是上划中央收
入,给出现期量、增长量;r=增长量/基期量=16.02/(47.57-16.02)
=16.02/31.X≈1/2=50%,最接近C项。【选C】
【注意】如果列式为16.02/47.57,首位商3,则会错选A项。
42【练习2】(2021江苏)在我国主要海洋产业中,2019年产值年增量最大的
是:
A.滨海旅游业 B.海洋船舶工业
C.海洋油气业 D.海洋工程建筑业
【解析】练习 2.课堂正确率为 89%。“增量最大”→增长量比较问题,结合
选项的主体定位材料找数据。A项滨海旅游业:18086、9.3%;B项海洋船舶工业:
1182、11.3%;C项海洋油气业:1541、4.7%;D项海洋工程建筑业:1732、4.5%。
A、C、D项比较:A项的现期量大、r大,排除C、D项。比较A、B项:两者的r
差不多,现期量之间有量级差距(18086/1182=10+倍),现期量大的增长量大,
则A项增长量大,对应A项。【选A】
【注意】
1.“滨海旅游业”在材料中排在最后,注意不要错选D项;选项和材料的顺
序不一致,需要注意顺序陷阱。
2.增长量比较:优先利用“大大则大”,如果现期量之间存在10+倍的关系(量
级的差距),直接根据现期量的量级进行判定。
作业:
431.巩固:今天的题下次课之前再做一遍
2.预习:比重、平均数
【答案汇总】
一般增长率计算1-5:BDCCB;6:A
一般增长率比较1-3:CAC
增长量计算1-5:ACBBC;6-8:BCD
增长量比较1-4:BBAA
44遇见不一样的自己
Be your better self
45