文档内容
方法精讲-资料 3
(笔记)
主讲教师:邓建
授课时间:2024.05.31
粉笔公考·官方微信方法精讲-资料 3(笔记)
资料分析 方法精讲3
学习任务:
1.课程内容:比重、平均数
2.授课时长:3小时
3.对应讲义:第 191~201页
4.重点内容:
(1)现期比重、基期比重的题型识别及计算公式
(2)两期比重的题型识别、升降判断及数值计算
(3)不同条件下的现期平均数、基期平均数计算及两期平均数问题
【注意】上节课课后作业回顾:
1.增长率计算题型识别:增长/下降+%;增长量计算题型识别:增长/下降+
单位(例如元、万、人)。
2.已知今年增长率和去年增长率相比提高了 x个百分点,求去年增长率用减
法;已知今年增长率和去年增长率相比降低了 x个百分点,求去年增长率用加法
(高减低加)。
3.已知现期量和基期量,增长率计算公式为(现期- 基期)/基期;r 的核
心公式→增长量/基期。已知现期量和增长量,增长率计算公式为增长量/(现期
-增长量)。
4.增长率比较题型识别:问增长最快/慢;增长量比较题型识别:问增长最
多/少。
5.增长率比较,先看“现期/基期”的倍数(谁的倍数大→谁的增长率大),
看不出来(若都是 1+倍)再比较增长量/基期(分数比较→钱多人少的思维)。
增长量在变大,基期在变小,则 r变大。
6.若增长率为 r,则现期量是基期量的 r+1倍。倍数=r+1、r=倍数-1。例如
今年比去年增长 30%,则今年是去年的 1.3倍。
17.已知现期量和基期量,增长量计算公式为现期- 基期;已知现期量和增长
率,求增长量:百化分,先将|r|=1/n,则增长量等于现期/(n+1),下降量等
于现期/(n-1)。
8.年均增长量计算公式为(现期- 基期)/n;一般情况,对于 2011~2015
年间,现期为2015 年,基期为2011年,年份差为4;“十二五”期间(再如“十
三五”期间→2016~2020 年,现期为 2020 年,基期为 2015 年),现期为 2015
年,基期为 2010 年,年份差为5(“十几五”规划期间年份差一定是 5)。
9.增长量的比较,若现期量大、r 大,则增长量大;若一大一小,则百化分
(最稳妥)或看倍数(两者倍数差距明显,倍数大的说得算;若两者倍数接近,
例如都是1+、2+倍,就用百化分),实际做题看倍数可以搞定。
第五节 比重
基本术语:
比重
比重指部分在整体中所占的比率,贡献率、利润率等也可以看成比重。
增长贡献率
增长贡献率指部分增量在整体增量中所占的比例。
利润率
资料分析中的利润率特指利润在收入中的占比。
【注意】本节课是整个资料分析中最核心的部分,占据资料分析的半壁江山,
比例相关的变形方式很多,考查很灵活。
关键字:占
一、现期比重(必考、简单)
二、基期比重(考得少、分析)
三、两期比重(常考、技巧强)
【注意】比重:关键词→“占”,部分在总体中所占比例,例如男生比重→
男生(1000 人)/总人数(4000 人)=1/4=25%、女生比重→女生/总人数(4000
人)。
21.现期比重(考查最多、必考、简单)。
2.基期比重(考得少、分析)。
3.两期比重(常考、技巧强)。
一、现期比重
题型识别:求现在,出现“占”
①A 占B的比重:湖北人口数占全国的比重
②在 B中,A占的比重:在全班总人数中,男生所占的比重
公式:比重=部分(A)/总体(B)
【注意】现期比重:
1.识别:求现在(问题时间与材料时间一致),出现“占”,求今年的占比,
或求今年的部分量、总体时会利用到占比。
(1)A占B 的比重:例如湖北人口数占全国的比重→比重=“占”前/“占”
后=湖北/全国。
(2)在B中 A所占的比重:例如在全班总人数中,男生所占的比重→男生/
全班,用“小的量/大的量”。
2.公式:比重=部分(A)/总体(B)。本节课思维导图中很多公式都与 A
和 B 相关,在数学中 A、B 就是英文字母,而资料分析中人为的定义→所有的一
步除法都有用“A/B”的结构表示“分子/分母”,因此不同的公式中含义一样,
A→分子对应的量,B→分母对应的量。
3【例 1】(2024 联考)2023 年 6 月 J 省深圳证券交易所证券当期成交金额
占上半年的比重为:
A.不到 15% B.15%~20%
C.20%~25% D.超过25%
【解析】1.主体为 J 省深圳证券交易所证券当期成交金额,6 月比重=6 月/
上半年(1~6月),注意不要将表格中的 1月、……、6月全部相加计算上半年
(约 970),289/970 会误选 D 项,累计→2023 年 6 月的累计即是 1~6 月,资
料分析中看到“累计”要警惕,表格中的 5 月代表 1~5 月的值,则实际的 6 月
=1~6月-1~5 月≈289-240=49,所求≈49/290,首位商1,排除 C、D项;49/29
的首位商1,次位商 5,结果=15+%,对应 B项。【选B】
【注意】本题材料中的数据有规律→每个月都在升高,表格中的 11 月是 1
月的十几倍,逐渐升高说明是累加上去的,再关注表格的横纵标目,发现的确是
累计数据。
2023 年前 5 个月,天津口岸出口汽车约 17.2 万辆,同比增长 29.5%,总价
值约100.1 亿元人民币,同比增长 40.2%。
2023 年前 5 个月,汽车出口带动天津口岸整体出口同比增加。汽车出口占
同期天津口岸出口商品总值的 2.2%,较上年同期提升 0.3 个百分点。1~5 月民
营企业出口活力明显,民营企业出口约 10.6 万辆,同比增长 64.3%,占同期天
津口岸汽车出口总量的 61.6%,占比较上年同期提升 13 个百分点。新能源汽车
出口成为新的增长点,出口约 11万辆,同比增长 50.2%。
【例 2】(2024联考)2023年1~5月,天津口岸出口商品总值在以下哪个
范围内?
A.不到 4000 亿元 B.4000~4400亿元之间
C.4400~4800 亿元之间 D.4800亿元以上
【解析】2.问题时间与材料时间一致,为现期时间;根据“汽车出口带动天
津口岸整体出口同比增加。汽车出口占同期天津口岸出口商品总值的 2.2%”、
“总价值约100.1 亿元人民币”可知,汽车出口/出口总值=2.2%→所求(出口总
4值)≈100/2.2%,不要将2.2%看成1/50,100*50=5000,从而错选 D项;100/2.2%
的首位商 4,B、C、D项均为4开头,需要确定是4千几,次位商 5,结果45开
头,对应 C项。【选 C】
【注意】比重=部分/总体、总体=部分/比重。
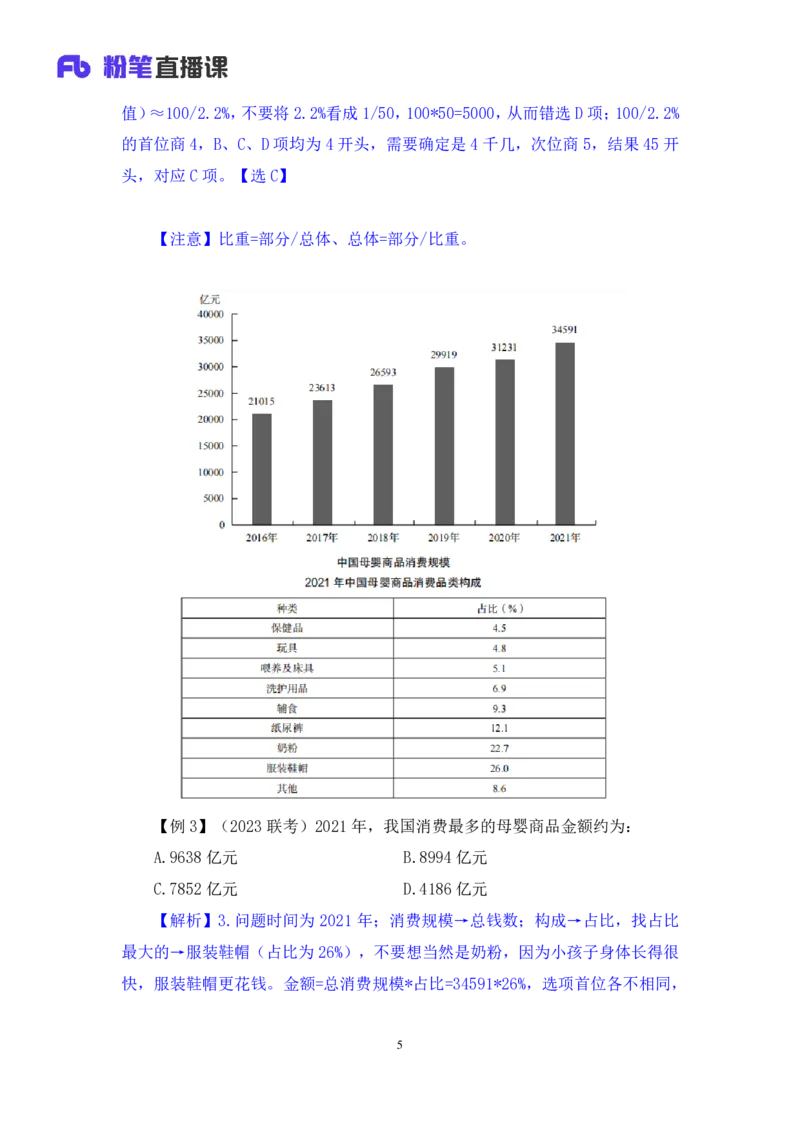
【例 3】(2023联考)2021年,我国消费最多的母婴商品金额约为:
A.9638 亿元 B.8994亿元
C.7852 亿元 D.4186亿元
【解析】3.问题时间为 2021 年;消费规模→总钱数;构成→占比,找占比
最大的→服装鞋帽(占比为26%),不要想当然是奶粉,因为小孩子身体长得很
快,服装鞋帽更花钱。金额=总消费规模*占比=34591*26%,选项首位各不相同,
5选项差距大,结合百化分,26%≈25%=1/4,所求≈34591/4,首位商 8,结果 8
开头,对应 B项。【选 B】
【注意】
1.只有精确的加减法(不存在四舍五入的情况下)才用尾数法,除法几乎没
有能整除的,乘法几乎存在四舍五入,故乘除法不能用尾数法。例如本题
34591*0.26,结果会有小数点后两位,但选项中没有小数点后两位。
2.百化分不是公式,而是数字本身的规律(所有百分数都能转化为分数),
求增长量时将百化分套到公式里化简出新的公式,与增长量计算捆绑最深,但实
际其他地方涉及到百分数的乘除运算都可以用百化分简化计算,例如111/14.3%,
14.3%≈1/7,原式→111*7=777。
3.本题的误差分析:34000*1%=300+,而选项差距是几千,因此将 26%看成
1/4不影响选答案。乘法的计算→如果选项差距大时,近似取整估算,结合选项、
范围选答案;如果选项差距小时,需要算得更精确,利用百化分结合拆分。如果
将本题的选项改为 8648、8994、8852、8768,选项差距小,26%=25%+1%=1/4+1%,
34591/4+34591*1%=8600++345=8900+,选择B项。再如34%=33.3%(1/3)+0.7%。
2020 年前三季度,G 省智能机器人产业实现营业收入 326.62 亿元,同比增
长超40%,四大行业营业收入均实现正增长,经济效益好于全部规模以上工业企
业。
【例 4】(2021 广东)2020 年前三季度,G 省智能机器人产业的总体利润率
(利润率=利润总额/营业收入)约为:
A.-0.6% B.4.6%
C.9.6% D.14.6%
【解析】4.问题时间与材料时间一致,为现期时间;问 G省智能机器人产业
6的总体利润率,利润率=利润总额/营业收入(资料分析统计收入利润率;数量关
系→利润率=利润/成本),相当于求现期比重。已知“2020 年前三季度,G 省智
能机器人产业实现营业收入 326.62 亿元”,材料没有总利润,表格给出四个利
润,资料分析常见总分结构、和差关系,机器人产业分为四大行业(若没说有其
他的就默认是这四个,不放心可以将这四个的收入加起来验证是否是 326.62,
验证后是正确的),四个利润之和是总体的利润,有正有负,加和要抵消,
(-8.61+0.22+40.74-0.9)/326.62,0.74、0.22 和-0.90 近似抵消,分子≈
40-8.6=31.4,原式≈31.4/326>0,排除 A 项;资料分析是选择题,不要“死”
算,326*10%=32.6,分子 31.4 接近 32.6,且只小一点点,说明结果比 10%小一
点点,最接近 C 项。【选C】
【注意】截位是计算的方法,有选项,能不算就不算。
2022 年中国锂电池出货量 658GWh,同比增长101.1%。2022 年中国动力锂电
池装车量达 294.6GWh,同比增长 90.7%,高于全球同比增速 18.9 个百分点,占
全球动力锂电池装车量的 56.9%。
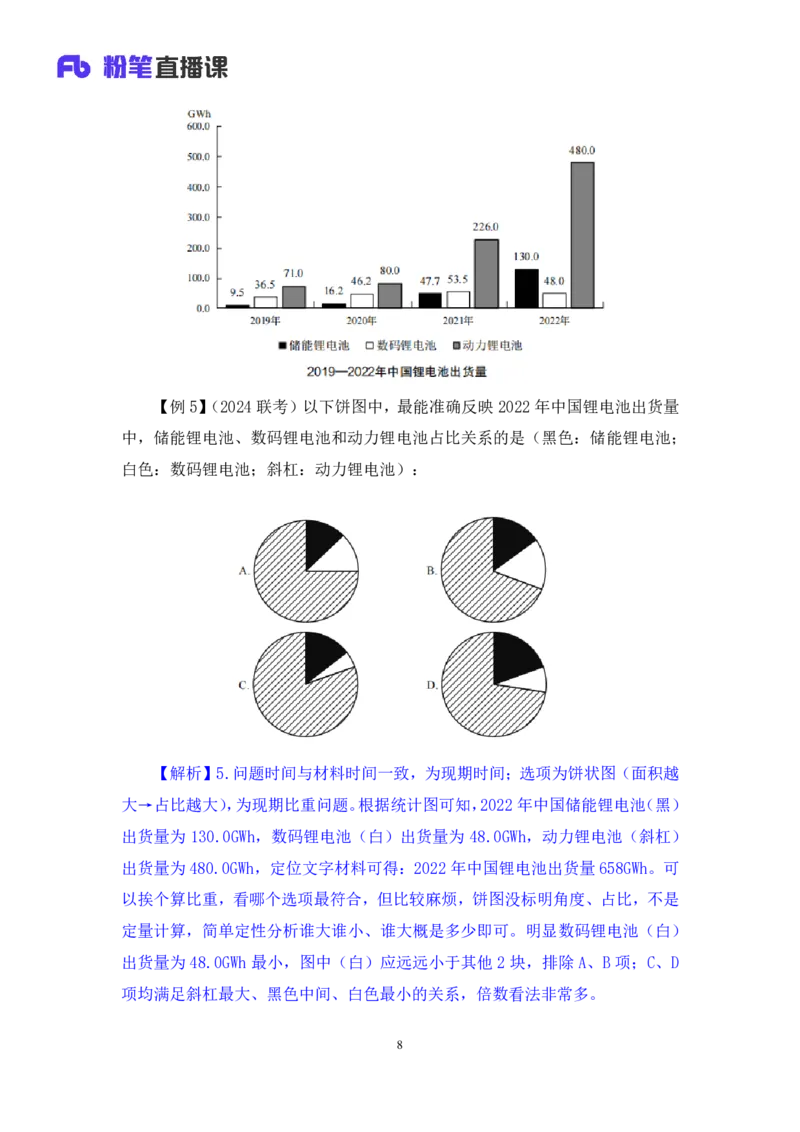
7【例 5】(2024 联考)以下饼图中,最能准确反映 2022 年中国锂电池出货量
中,储能锂电池、数码锂电池和动力锂电池占比关系的是(黑色:储能锂电池;
白色:数码锂电池;斜杠:动力锂电池):
【解析】5.问题时间与材料时间一致,为现期时间;选项为饼状图(面积越
大→占比越大),为现期比重问题。根据统计图可知,2022年中国储能锂电池(黑)
出货量为 130.0GWh,数码锂电池(白)出货量为 48.0GWh,动力锂电池(斜杠)
出货量为480.0GWh,定位文字材料可得:2022年中国锂电池出货量 658GWh。可
以挨个算比重,看哪个选项最符合,但比较麻烦,饼图没标明角度、占比,不是
定量计算,简单定性分析谁大谁小、谁大概是多少即可。明显数码锂电池(白)
出货量为 48.0GWh 最小,图中(白)应远远小于其他 2 块,排除 A、B 项;C、D
项均满足斜杠最大、黑色中间、白色最小的关系,倍数看法非常多。
8角度 1:480/130=3+→斜杠>黑色*3(直接用手比划),C 项能画出5、6倍,
排除,对应D项。
角度 2:斜杠/白色=480/48=10,可以用量角器量,但比较浪费时间,不建
议用量角器。
角度 3:C、D 项最大的区别是黑+白一个是锐角,一个是钝角,看占比是否
超过 1/4(90°),总量 658/4=160+<130+48=178,故黑+白的占比超过 1/4,饼
图上是>90°,对应 D项。【选D】
【注意】本题还可以看3/4或斜杠是否超过(黑+白)的 3倍。
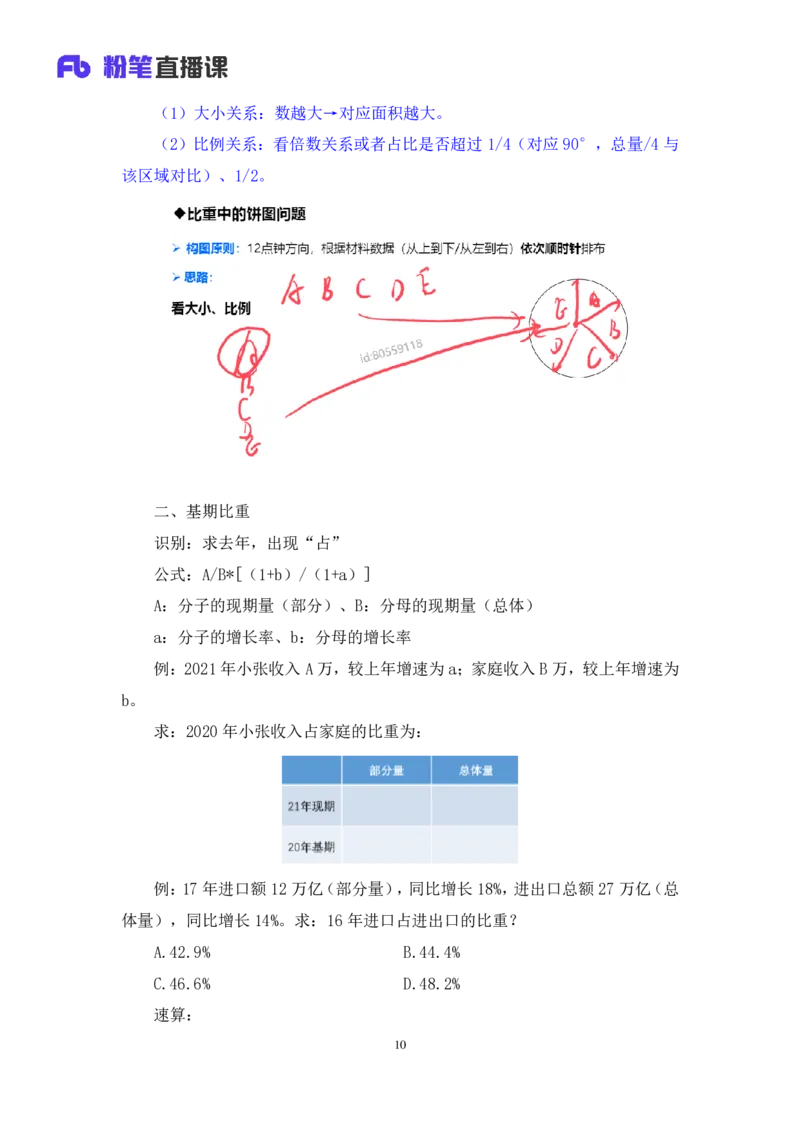
比重中的饼图问题
构图原则:12点钟方向,根据材料数据(从上到下/从左到右)依次顺时针
排布。
思路:看大小、比例
【注意】比重中的饼图问题:
1.构图原则:12点钟方向,根据材料数据(从上到下/从左到右)依次顺时
针排布。用作图软件画图,例如数据的输入顺序从左到右是 A、B、C、D、E,从
12点钟方向,根据输入数据的顺序,顺时针依次排布(依次对应第 1、2、3、4、
5块)。例如数据的输入顺序从上到下是A、B、C、D、E,从 12点钟方向,根据
输入数据的顺序,顺时针依次排布(依次对应第 1、2、3、4、5块)。
2.思路:看大小、比例。
9(1)大小关系:数越大→对应面积越大。
(2)比例关系:看倍数关系或者占比是否超过1/4(对应 90°,总量/4与
该区域对比)、1/2。
二、基期比重
识别:求去年,出现“占”
公式:A/B*[(1+b)/(1+a)]
A:分子的现期量(部分)、B:分母的现期量(总体)
a:分子的增长率、b:分母的增长率
例:2021年小张收入 A万,较上年增速为 a;家庭收入 B万,较上年增速为
b。
求:2020年小张收入占家庭的比重为:
例:17年进口额 12万亿(部分量),同比增长18%,进出口总额 27万亿(总
体量),同比增长 14%。求:16年进口占进出口的比重?
A.42.9% B.44.4%
C.46.6% D.48.2%
速算:
10一般先计算 A/B(现期比重,材料可能给出)
再看右边(1+b)/(1+a)与1的大小关系,结合选项分析
【注意】基期比重(难点):
1.识别:求去年,出现“占”。
2.公式:A/B*[(1+b)/(1+a)]。A:分子的现期量(部分)、B:分母的
现期量(总体)、a:分子的增长率、b:分母的增长率。
3.推导:2021 年小张收入A万,较上年增速为 a;家庭收入 B万,较上年增
速为b。求:2020 年小张收入占家庭的比重为:
答:问题时间在材料时间之前,为基期时间;问“……占……的比重”,为
基期比重问题。2020 年小张收入=A/(1+a),2020 年家庭总收入=B/(1+b),
所求占比=A/(1+a)÷[B/(1+b)]=A/(1+a)*[(1+b)/B]=A/B*[(1+b)/(1+a)]。
4.例:17年进口额 12万亿(部分量),同比增长 18%,进出口总额 27万亿
(总体量),同比增长 14%。求:16年进口占进出口的比重?
A.42.9% B.44.4%
C.46.6% D.48.2%
答:问题时间在材料时间之前,为基期时间;问“……占……的比重”,为
基期比重问题;公式:A/B*[(1+b)/(1+a)]。比重=进口(对应A、a)/进出
口(对应B、b),列式:12/27*(1+14%)/(1+18%)。多步乘除,选项差距很
小,可以截3位硬算,但浪费时间。复杂的基期的和差、乘除→分析答案的范围
→算一半,看选项。先算现期比重→12/27=4/9,1/9≈11.1%→4/9≈44.4%→B
项是现期坑,以坑治坑,排除 B 项;(1+14%)/(1+18%)的分子<分母,分数
值小于1,结果→44.4%*1-<44.4%,仅 A项符合。
5.速算:资料分析→重在分析,不招计算器。
(1)一般先计算 A/B(现期比重,材料可能给出)。
(2)再看右边(1+b)/(1+a)与 1 的大小关系,结合选项分析(范围)。
若有多个符合,一定会在选项和数据上设置逻辑让考生进行分析。
2018 年,针叶原木从新西兰进口 1729.4 万立方米,同比增长 23.2%;俄罗
斯 795.3 万立方米,下降 10.1%;美国 502.8 万立方米,增长 2.3%;澳大利亚
11413.4万立方米,下降 3.7%;乌拉圭 209万立方米,增长 175.4%;日本 92.3万
立方米,增长 23%。2018 年进口针叶锯材 2488 万立方米,金额 49.91 亿美元,
分别下降 0.7%和增长 2.3%。其中来自俄罗斯针叶锯材 1567.4 万立方米,增长
9.7%,占进口针叶锯材 63%,从加拿大进口 417.4 万立方米,大幅下降 18.2%,
占进口针叶锯材的 17%。
【例 1】(2021 新疆)2017 年从加拿大进口的针叶锯材占总进口的比重约
为:
A.62.70% B.40.25%
C.34.68% D.20.37%
【解析】1.问题时间在材料时间之前,为基期时间;问“……占……的比重”,
为基期比重问题;公式:A/B*[(1+b)/(1+a)]。比重=加拿大进口(对应 A、
a)/总进口(对应 B、b),不要如此列式:417.4/2488*[(1-0.7%)/(1-18.2%)],
根据“2018年……从加拿大进口……,占进口针叶锯材的 17%”可知,直接给出
A/B=17%,选项均>17%,一定会设置逻辑进行分析。若数字敏感度高,发现
1-0.7%=99.3%是1-18.2%≈82%的1倍多一点,直接选D项;或者发现C项(34.68%)
约是17%的2倍,就分析(1-0.7%)/(1-18.2%)是否到2,99.3%和81.8%一定
不到2倍关系,故结果一定<34%,仅 D项满足。【选D】
【注意】Tips:现在出题人往往喜欢给出现期比重,注意利用材料已有数据。
12【例 2】(2024 黑龙江)2021 年农村公路交通固定资产投资额占公路交通
固定资产投资额的比重为:
A.15.7% B.16.5%
C.17.4% D.19.5%
【解析】2.问题时间在材料时间之前,为基期时间;问“……占……的比重”,
为基期比重问题;公式:A/B*[(1+b)/(1+a)]。比重=农村(对应A、a)/公
路总和(对应B、b),代入数据,所求=4733/28527*[(1+9.7%)/(1+15.6%)],
公式中的a、b的位置不要记错,选项差距小,只能老老实实地算,先算4733/28527,
一步除法,分母截 3位转化为4733/285,首位商 1,次位商 6,计算到这就可以
了,A/B=16.X%,对应 B 项,这是现期坑,排除 B 项;(1+9.7%)/(1+15.6%)
的分子<分母→(1+9.7%)/(1+15.6%)<1,结果=16.X%*1-<16.X%,仅 A 项
满足。【选A】
【注意】
1.选项差距大→多步乘除→分子分母均截 2位;选项差距小→多步乘除→分
子分母均截3位,但对于本题,这样计算量较大。
2.若不放心,可以算出 4733/285 的第三位→商5,结果<16.5+%,仅A项满
足。
2018 年 1~10 月份,全国房地产开发投资 99325 亿元,同比增长 9.7%,增
速比1-9月份回落 0.2个百分点。其中,住宅投资 70370亿元,增长 13.7%,增
速回落0.3个百分点。住宅投资占房地产开发投资的比重为 70.8%。
【练习】(2019 青海)2017年1~10月,住宅投资占房地产开发投资的比重
约为:
A.68.4% B.70.8%
C.72.8% D.73.4%
【解析】拓展.问题时间 2017 年 1~10 月,出现“比重”,基期比重问题,
对应材料,A/B*[(1+b)/(1+a)]=70.8%*[(1+9.7%)/(1+13.7%)]=70.8%*1-
<70.8%,对应 A项。【选A】
13【注意】
1.现在出题人往往喜欢给出现期比重,注意利用材料已有数据。
2.变形:假设把a和b弄反,变为70.8%*[(1+13.7%)/(1+9.7%)]=70.8%*1+,
排除A、B项;(1+13.7%)/(1+9.7%)=(1+9.7%+4%)/(1+9.7%),原式=70.8%*[1+4%/
(1+9.7%)]≈70.8%+70.8%*4%/1.1≈70.8%+2.5%=73.3%,对应 D项。
三、两期比重
两期比重——比较
识别:两个时间+比重+升降
例:2021年,小马收入占家庭总收入的比重与去年相比:
A.提高 B.降低
C.不变
现期比重=A/B
基期比重=A/B*[(1+b)/(1+a)]
【注意】两期比重——比较:
1.识别:两个时间+比重+升降。
2.例:2021 年,小马收入占家庭总收入的比重与去年相比:
A.提高 B.降低
C.不变
答:问 2021 年和去年相比,比重是提高还是降低,两期比重的比较。
3.你的收入(a)/总收入(b),假设你的收入增长得很快,但是家庭的总
收入没怎么变,你的占比就会越来越高。假设你的收入没怎么涨,家庭的总收
入一直涨,则你的占比就越来越低。
4.现期比重=A/B,基期比重=A/B*[(1+b)/(1+a)]。
(1)如果 a>b,则A/B*1-<A/B→a>b,现期比重>基期比重。
(2)如果 a<b,则A/B*1+>A/B→a<b,现期比重<基期比重。
14判断方法:
a>b,比重比去年上升;
a<b,比重比去年下降;
a=b,比重不变。
比重=部分(A、a)/总体(B、b)
a:分子的增长率,b:分母的增长率
比较时需带正负号比较
练习:2019 年总收入 10 万元,同比增长 10%,工资收入 8 万,同比增长
5%。则 2019年工资收入占总收入的比重比上年上升还是下降?
【注意】两期比重——比较:
1.判断方法:
(1)a>b,比重比去年上升。
(2)a<b,比重比去年下降。
(3)a=b,比重不变。
2.比重=部分(A、a)/总体(B、b):
(1)a:分子的增长率,b:分母的增长率。
(2)比较时需带正负号比较。
3.练习:2019 年总收入 10 万元,同比增长 10%,工资收入 8 万,同比增
长5%。则 2019 年工资收入占总收入的比重比上年上升还是下降?
答:工资收入为 a,总收入为b,a=5%<b=10%,比重下降。
【例 1】(2023 联考)据对全国 6.4 万家规模以上文化及相关产业企业调查,
2021 年前三季度,上述企业实现营业收入 84205 亿元,按可比口径计算,同比
增长21.8%,两年平均增长 10.0%。
15分行业类别营业收入情况:新闻信息服务 9847 亿元,同比增长 22.1%;内
容创作生产 17693 亿元,同比增长18.6%;创意设计服务 13787 亿元,同比增长
24.0%;文化传播渠道 9309 亿元,同比增长 30.1%;文化投资运营 359 亿元,同
比增长 13.8%;文化娱乐休闲服务 916 亿元,同比增长 35.3%;文化辅助生产和
中介服务11441亿元,同比增长18.3%;文化装备生产4880亿元,同比增长17.8%;
文化消费终端生产 15974亿元,同比增长 22.0%。
与上一年相比,2021 年前三季度分行业类别中,占全国 6.4 万家规模以上
文化及相关产业企业营业总收入比重增加的行业个数是:
A.3 个 B.4个
C.5 个 D.6个
【解析】1.两个时间,问比重增加→a>b,比重上升;各种各样的行业类别
对应a,全国对应 b,对应材料,b=21.8%,就找大于21.8%的,有 5个满足,对
应C项。【选C】
【例 2】(2021 四川)2019 年,我国电信业务收入完成 1.31 万亿元,比上
年增长0.8%。其中:固定数据及互联网业务收入完成2175亿元,比上年增长5.1%;
移动数据及互联网业务收入6082亿元,比上年增长1.5%;固定增值业务收入1371
亿元,比上年增长 21.2%,其中,IPTV(网络电视)业务收入 294亿元,比上年
增长21.1%;物联网业务收入比上年增长 25.5%。
下列指标中,2019年的数值高于 2018年的有几项?
①固定数据及互联网业务收入占电信业务收入比重
②移动数据及互联网业务收入占电信业务收入比重
③IPTV 业务收入占固定增值业务收入比重
A.0 B.1
C.2 D.3
16【解析】2.要2019年比重要高于上年,比重上升→a>b,a是分子,b是分
母。
①固定业务 a=5.1%>电信业务b=0.8%,比重上升,满足。
②移动业务 a=1.5%>电信业务b=0.8%,比重上升,满足。
③IPTV 业务 a=21.1%<固定增值业务 b=21.2%,比重下降,不满足。对应 C
项。【选 C】
两期比重——计算:
识别:比重+上升/下降+几个百分点
例:2020年,邓同学的收入占家庭总收入的比重比上年同期:
A.上升了 1.1 个百分点 B.上升了5.1个百分点
C.下降了 1.1 个百分点 D.下降了5.1个百分点
公式:现期比重- 基期比重=A/B-A/B*[(1+b)/(1+a)]=A/B*[(a-b)/
(1+a)]。
方法:
1、判升降(a>b,上升;a<b,下降)
2、定大小:比重差<|a-b|
【例 1】a=8.5%,b=9.5%。
A.增加了 3 个百分点 B.减少了3个百分点
C.增加了 0.3 个百分点 D.减少了0.3个百分点
【例 2】a=13.8%,b=12.5%。
A.增加了 0.5 个百分点 B.增加了1.3个百分点
C.减少了 0.5 个百分点 D.减少了1.3个百分点
【例 3】a=-10%,b=5%。
A.增加了 15 个百分点 B.增加了1.3个百分点
C.减少了 15 个百分点 D.减少了1.3个百分点
【注意】两期比重——计算:
1.识别:比重+上升/下降+几个百分点。
2.例:2020 年,邓同学的收入占家庭总收入的比重比上年同期:
17A.上升了 1.1 个百分点 B.上升了5.1个百分点
C.下降了 1.1 个百分点 D.下降了5.1个百分点
答:比重问升降是两期比重的升降,如果还问了几个百分点,就是两期比重
计算。
3.公式:现期比重- 基期比重=A/B-A/B*[(1+b)/(1+a)]=A/B*[1-(1+b)
/(1+a)]=A/B*{[1+a-(1+b)]/(1+a)}=A/B*[(a-b)/(1+a)]。
4.方法:
(1)判升降(a>b,上升;a<b,下降)。
(2)定大小:比重差<|a-b|,就用大的-小的。
①假设 A/B=50%,a=10%,代入公式中,50%*[(a-b)/(1+10%)]=50%*(a-b)
/1.1→(a-b)*1-<a-b。
②极端情况会不成立,但是可以先不管,后面会补充。
5.练习:
(1)例1:a=8.5%,b=9.5%。
A.增加了 3 个百分点 B.减少了3个百分点
C.增加了 0.3 个百分点 D.减少了0.3个百分点
答:a<b,比重下降,排除 A、C 项;比重差<|8.5%-9.5%|,就用大-小,
结果<1 个百分点,对应 D项。
(2)例2:a=13.8%,b=12.5%。
A.增加了 0.5 个百分点 B.增加了1.3个百分点
C.减少了 0.5 个百分点 D.减少了1.3个百分点
答:a>b,比重上升,排除 C、D 项;大-小为 13.8%-12.5%=1.3%,选小于
的,对应A项。
(3)例3:a=-10%,b=5%。
A.增加了 15 个百分点 B.增加了1.3个百分点
C.减少了 15 个百分点 D.减少了1.3个百分点
答:a<b,比重下降,排除 A、B项;大-小为5%-(-10%)=15%,选小于的,
对应D项。
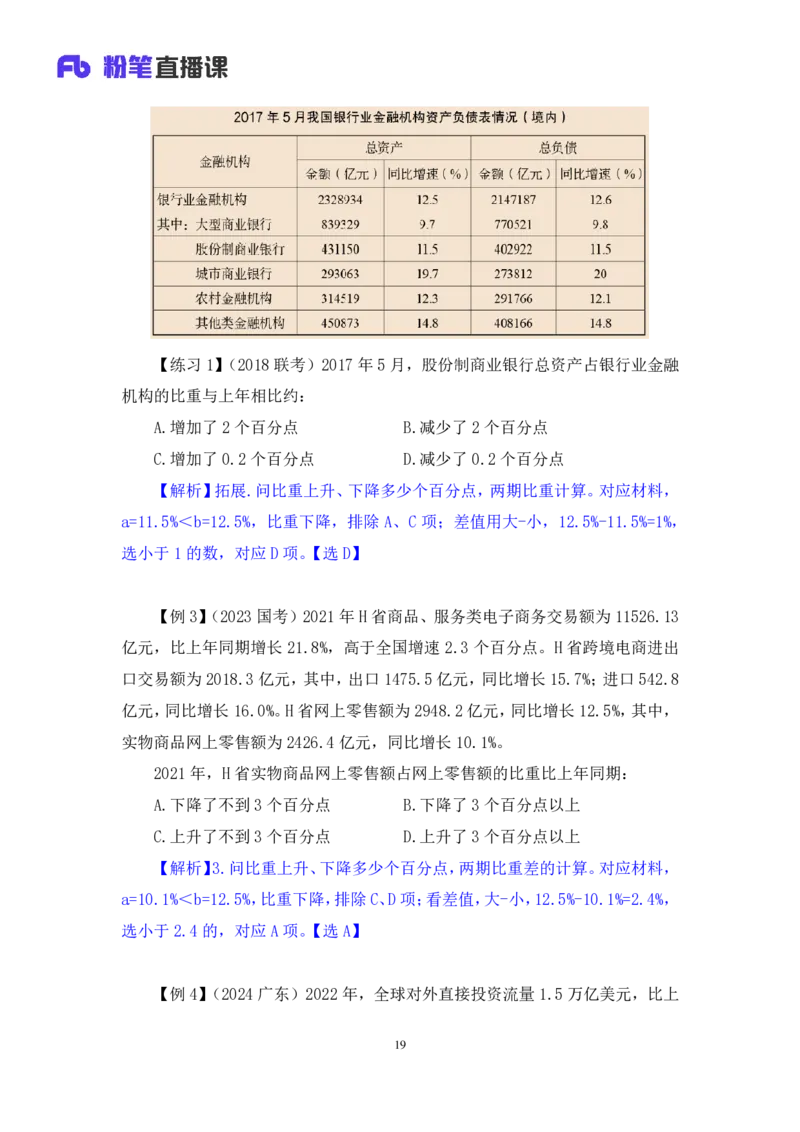
18【练习 1】(2018联考)2017年5 月,股份制商业银行总资产占银行业金融
机构的比重与上年相比约:
A.增加了 2 个百分点 B.减少了2个百分点
C.增加了 0.2 个百分点 D.减少了0.2个百分点
【解析】拓展.问比重上升、下降多少个百分点,两期比重计算。对应材料,
a=11.5%<b=12.5%,比重下降,排除 A、C 项;差值用大-小,12.5%-11.5%=1%,
选小于1的数,对应 D项。【选D】
【例 3】(2023 国考)2021年H省商品、服务类电子商务交易额为 11526.13
亿元,比上年同期增长 21.8%,高于全国增速 2.3 个百分点。H 省跨境电商进出
口交易额为2018.3 亿元,其中,出口 1475.5亿元,同比增长 15.7%;进口542.8
亿元,同比增长 16.0%。H省网上零售额为 2948.2亿元,同比增长 12.5%,其中,
实物商品网上零售额为2426.4亿元,同比增长 10.1%。
2021 年,H 省实物商品网上零售额占网上零售额的比重比上年同期:
A.下降了不到 3个百分点 B.下降了3个百分点以上
C.上升了不到 3个百分点 D.上升了3个百分点以上
【解析】3.问比重上升、下降多少个百分点,两期比重差的计算。对应材料,
a=10.1%<b=12.5%,比重下降,排除C、D项;看差值,大-小,12.5%-10.1%=2.4%,
选小于2.4的,对应 A项。【选A】
【例 4】(2024 广东)2022 年,全球对外直接投资流量 1.5万亿美元,比上
19年下降 14%。其中发达经济体对外直接投资 1.03 万亿美元,比上年下降 17.2%;
发展中经济体对外直接投资 4589亿美元,比上年下降 5.4%。
2022 年,中国对外直接投资流量 1631.2 亿美元,与上年历史次高值相比,
下降8.8%,占全球份额的 10.9%。
与 2021年相比,2022年中国对外直接投资流量在全球中的占比:
A.增加了不到 3个百分点 B.增加了超过3个百分点
C.减少了不到 3个百分点 D.减少了超过3个百分点
【解析】4.问比重的升降,先找 a 和 b,对应材料,a=-8.8%,b=-14%,负
得越少值越大,则 a>b,排除C、D项。差值为 14%-8.8%=5.2%,选比 5.2小的,
锁定不了答案。代入公式,A/B*[(a-b)/(1+a)]=10.9%*[(-8.8%)-(-14%)]/
(1-8.8%)=(10.9%*5.2%)/(1-8.8%)≈0.5%/0.912≈0.6%,增加了不到 3
个百分点,对应 A项。【选A】
三、两期比重——计算
识别:比重+上升/下降+几个百分点
公式:现期比重− 基期比重=A/B*[(1+b)/(1+a)]
方法:
1、判升降(a>b,上升;a<b,下降)
2、定大小:比重差<|a-b|
注:
①若选项中只有一个小于|a-b|,秒杀(80%的题目如此)
②若选项中有多个小于|a-b|或没有,代公式快速估算
【注意】
1.举例:A/B=10%,a=-20%,代入公式,10%*[(a-b)/(1-20%)]=(a-b)
*10%/80%=(a-b)*1-<a-b。
2.极端反例:在 2022 年广东省考出现过 1 次,因为那几年受到疫情影响,
还是航空相关的例子。A/B=90+%,a=-30+%,代入公式,90+%*[(a-b)/(1-30+%)]
≈(a-b)*90+%/70%=(a-b)*1+>a-b,此时就代入公式计算。
202022 年,我国电信业务收入累计完成 1.58万亿元,比上年增长 8%,较2018
年增长超2800 亿元。
2022 年移动数据流量业务收入 6397 亿元,比上年增长 0.3%,在电信业务收
入中占比约为40.5%……
【练习 2】(2023 广东)与 2021 年相比,2022 年我国移动数据流量业务收
入在电信业务收入中的占比:
A.增加了约 3个百分点 B.减少了约3个百分点
C.增加了约 13个百分点 D.减少了约13个百分点
【解析】拓展.问占比增加减少几个百分点,先判断升降,a=0.3%<b=8%,
比重下降,排除 A、C 项;差值为8%-0.3%=7.7%,选小于7.7 的,对应 B项。【选
B】
第六节 平均数
关键字:平均每
题型:一、现期平均数(重点必考)
二、基期平均数(几乎不考)
三、两期平均数(常考,技巧性强)
【注意】
1.平均数的结构与比重一模一样,分为现期平均数、基期平均数和两期平均
数,除了平均数的增长率外,其他公式都与比重一模一样,故该部分更多讲解“运
用”,节奏会稍微轻快一点。
2.比重和平均数有一个关键性区别:比重关键词为“占比”,平均数的关键
词为“平均每”。
3.现期平均重点必考,基期平均考得非常少;两期平均与两期比重一样,常
考、技巧性较强。
一、现期平均数
识别:求现在+平均每(人均/单价)
公式:平均数=总数(A)/个数(B)
21计算形式:后/前
(1)人均收入=收入/人数
(2)单位面积产量=产量/面积
速算技巧:截位直除
【注意】
1.识别:求现在+平均每(人均/单价/单位面积/均/每/单)。
2.公式:平均数=总数/个数,如 100 亿分给 3920 人,则平均每人分的钱数
为100亿/3920 人。
3.现期平均数为一步直除,用“A/B”表示,A 表示分子、B表示分母,比重
中,A为部分、B为总体;平均数中无部分和总体,如果按照“部分/总体”进行
记忆,容易记混,建议直接记“A/B”,结合问题列出除法算式,就会知道谁是分
子、谁是分母。
4.计算形式:“后/前”。
(1)人均收入:收入在后、人数在前,列式为“收入/人数”。
(2)单位面积产量:产量在后、面积在前,列式为“产量/面积”。
5.速算技巧:若一眼看不出答案,就根据选项差距截位直除。
截至2020年底,全国基层群众性自治组织共计61.5万个,同比减少4.35%。
其中,村委会50.2 万个,占基层群众性自治组织的 81.63%,村民小组376.1万
个,村委会成员207.3万人;居委会11.3万个,占基层群众性自治组织的18.37%,
居民小组123.6 万个,居委会成员61.6 万人。2016~2020 年,我国村(居)委
会完成选举数分别为 9.7万个、18.2 万个、27.6万个、8.8 万个、6.1万个,其
中,2020 年村(居)委会登记选民数为 1.1 亿人,参与投票人数为 0.65 亿人。
【例 1】(2022 广东)2020 年,平均每个村委会下辖的村民小组约多少个?
A.3.5 B.5.5
C.7.5 D.9.5
【解析】1.问题时间与材料时间一致,出现“平均每”,为平均数问题,“下
辖”为动词,两个名词分别为“小组”和“村委会”,列式:小组/村委会=376.1/50.2,
首位商7,C项当选。【选C】
22【注意】每一个知识点都是由易到难,结合坑点进行适当补充。考试都是既
有简单题,又有难题。
2021 年上半年,湖北省 676家规上信息软件业企业中营业收入前 20的企业
共实现营业收入 355.46亿元,同比增长 8.3%,拉动规上服务业营业收入增长1.1
个百分点。
【例 2】(2022 湖北选调)2021年上半年湖北省规上信息软件业中营业收入
前20的企业,平均每家每月营业收入约为多少亿元?
A.1.18 B.2.25
C.2.32 D.2.96
【解析】2.平均每家营业收入=收入/企业数量,收入约为 355亿元,注意企
业数量不是676 家,平均数问题,分子好找,分母一定要找准,题干问的是“前
20 的企业”,则企业数量=20;注意本题还有一个细节,平均数问题最喜欢设置
的陷阱为“平均每月”,“355/20”是上半年的情况(上半年的总收入),要平均
到每个月,还需要除以 6,所求≈355/(20*6)=355/120≈3,D项当选。【选D】
【注意】
1.本题计算非常简单,要注意细节,平均数中有“每月”的设计,还要注意
分母的对应关系。
2.前半年是半年、6个月,不是一年。
【拓展】2013 年1~5月,保险业平均每月业务及管理费用约为多少亿元?
A.180 B.185
C.190 D.195
23【解析】拓展.求1~5月的平均值,列式:(1月+2月+3 月+4月+5月)/5,
这样做不好算。多个数加和后求平均值,考虑削峰填谷——在选项中挑一个夹在
中间、比较好算的数据,看每一个值比其多多少或少多少,最后再分析平均数。
选项居中的有185 和190,以185为基准,峰和谷分别为0、-19、+10、+4、+5,
0-19+10+4+5=0,正好抵消,则平均数=185,对应 B 项。这样除以一定比先加和
再除以5要简单得多。【选B】
【注意】多个数加和求平均值:削峰填谷(选一个选项中间好算的值)。
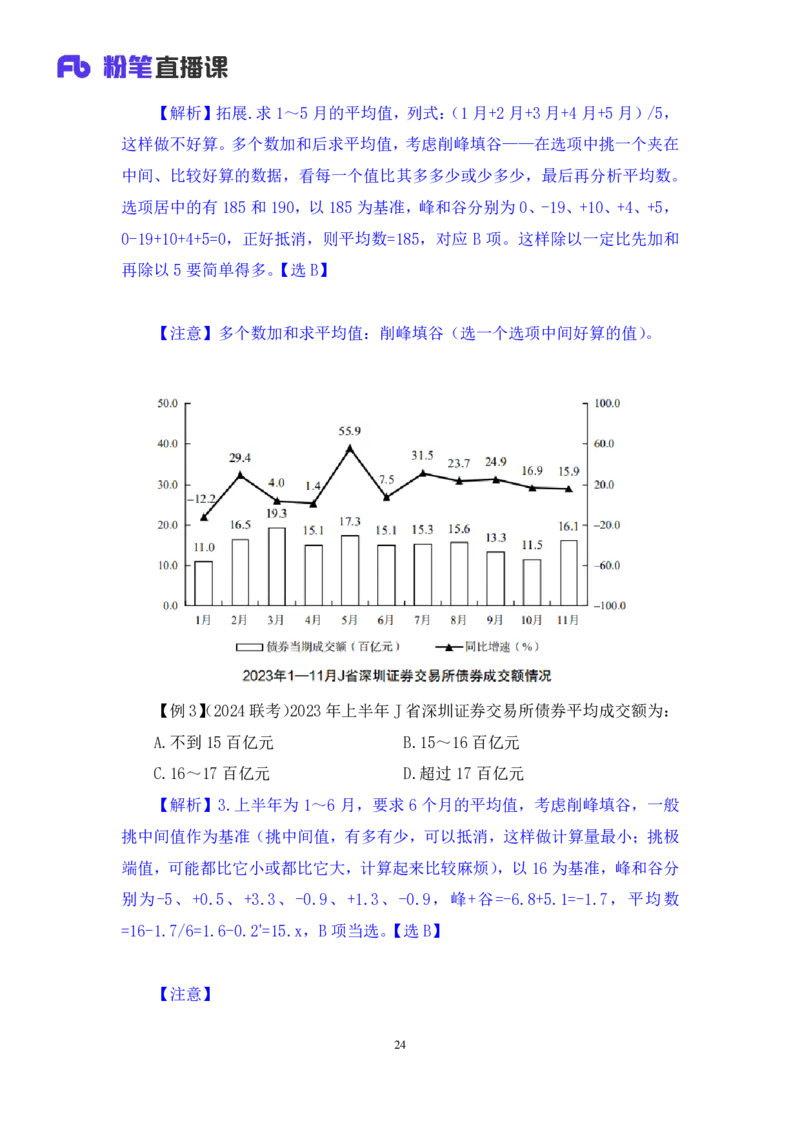
【例3】(2024联考)2023年上半年J省深圳证券交易所债券平均成交额为:
A.不到 15 百亿元 B.15~16百亿元
C.16~17百亿元 D.超过17百亿元
【解析】3.上半年为 1~6 月,要求 6 个月的平均值,考虑削峰填谷,一般
挑中间值作为基准(挑中间值,有多有少,可以抵消,这样做计算量最小;挑极
端值,可能都比它小或都比它大,计算起来比较麻烦),以 16 为基准,峰和谷分
别为-5、+0.5、+3.3、-0.9、+1.3、-0.9,峰+谷=-6.8+5.1=-1.7,平均数
=16-1.7/6=1.6-0.2+=15.x,B项当选。【选 B】
【注意】
241.基准可以是任意值,如本题,若基准定为 10,已知数据都比 10大,将峰
值全部加起来,与将原本的 6个数直接加和没有区别;如果能正负抵消,全部都
是个位数的口算的话,计算量就会小很多,故建议将基准定为选项中间比较整的
数。
2.平均数=基准+(峰+谷)/个数,峰、谷加和后得到的值是比总量多或少的
值,要求平均值,需要将其均摊到每个主体上,即需要除以数量。
3.本题可以将 11定为基准,此时只需要算 4个峰、谷。
【拓展】(2023国考)能够从上述资料中推出的是:
A.2016~2020 年,通用超算服务市场累计规模超过 160 亿元
【解析】拓展.A 项:累计规模=2016 年+2017 年+2018 年+2019 年+2020 年
=23.9+26.9+29.7+32.2+37.8,计算起来比较麻烦。要求 5 年之和>160 亿,等
价于平均每年>160/5=32 亿,若平均数>32 则总量>160,若平均数<32 则总
量<160。分析数据可知,仅 2020年比 32多 5.8、2019年约为 32,其他年份均
小于32(光是2016 年就比32就少了 8.1,2020年就已经补不起了),故平均数
<32,错误,不选。【不选】
【注意】
1.速算技巧:求 n年之和超过某个值时也可以比较平均数。
2.要求 10 年之和>500,10 个数据加和较麻烦,建议直接判断平均每年是
否超过50。
25二、基期平均数
识别:求去年+平均数
公式:A/B*[(1+b)/(1+a)](同基期比重公式)
A:分子现期量 B:分母现期量
a:分子增长率 b:分母增长率
速算:先计算现期平均 A/B,在观察(1+b)/(1+a)和 1 的关系,结合选
项分析
问:2016年人均收入
【注意】
1.基期平均数几乎不考、考得非常少,是考频很低的点,即使考了也没关系,
基期平均数与基期比重一模一样,因为现期比重=A/B、现期平均数=A/B,是一样
的形式,故基期比重、基期平均也都是一样的结构。
2.推导:给了 2017年的现期、r,要求 2016年的人均收入,人均收入=收入
/人数,收入对应 A、a,人数对应B、b,要求2016年的人均收入,需要将 2016
年的基期值表示出来,人均收入=收入/人数=A/(1+a)÷[B/(1+b)]=A/(1+a)
*[(1+b)/B]=A/B*[(1+b)/(1+a)],与基期比重的公式结构一模一样。
3.速算:先算 A/B,再看(1+b)/(1+a)是大于 1还是小于 1,结合选项选
答案。
2017年全国共有各级各类民办学校17.76万所,占全国学校总数的34.57%;
各类民办教育在校生达5120.47万人,比上年增长6.12%。其中:民办幼儿园16.04
万所,比上年增长 4.00%;在园儿童 2572.34 万人,比上年增长 5.53%。民办普
通小学 6107 所,比上年增长 2.21%;在校生 814.17 万人,比上年增长 7.65%。
民办初中5277 所,比上年增长3.78%;在校生 577.68万人,比上年增长 8.42%。
民办普通高中3002所,比上年增长7.71%;在校生306.26万人,比上年增长9.74%。
26民办中等职业学校 2069所,比上年下降 2.17%;在校生197.33 万人,比上年增
长7.16%。
【例 4】(2020 北京)2016 年平均每所民办中等职业学校在校生人数约为:
A.871 人 B.991人
C.1091 人 D.1181人
【解析】4.给 2017 年,问 2016 年,出现“平均每”,为平均数问题,平均
数=后/前=在校生人数/学校数,在校生人数对应 A、a,学校数对应 B、b。主体
为中等职业学校,根据公式:A/B*[(1+b)/(1+a)]≈197/2069*[(1-2.17%)
/(1+7.16%)]。选项差距比较小,197/2069 的分母截三位,化简为 197/207,
首位商9,最多到 B项;(1-2.17%)/(1+7.16%)→分子<分母→(1-2.17%)/
(1+7.16%)<1,B项*1-<B项,直接选 A项。【选A】
【注意】
1.若 B 项为 90x,则需要计算,但 B 项为 991,已经是选项中 9 开头的最大
数了,即只要确定首位商 9,最多取到 B 项,而(1-2.17%)/(1+7.16%)<1,
B项*1-<B项,有且只有 A项满足。
2.197/207,首位商9,次位商5,即 A/B≈950,排除B、C、D项;1-2.17%)
/(1+7.16%)<1,有且只有A项满足。
3.分子<分母→分数值<1;分子>分母→分数值>1,如 4/5<1、5/4>1。
4.课后一定要多看、多记几遍公式,课后也要做好预习和复习。
三、两期平均——比较(与两期比重升降方法相同)
识别:两个时间+平均数上升/下降
例:2019年,人均收入与 2018年相比?
A.上升 B.下降
C.不变 D.无法推出
方法:a>b,平均数上升;
a<b,平均数下降;
a=b,平均数不变。
27注:a:分子的增长率 b:分母的增长率
比较时需带正负号比较
【注意】
1.两期平均比较与两期比重升降方法相同,因为现期比重、现期平均数的公
式相同,基期比重、基期平均数的公式相同,可以类比记忆。
2.推导:假设收入增速为 a,人数增速为 b,若收入增长→a>0,人数不变
→b=0,每个人分到的钱变多→人均收入变高,即 a>b→平均数上升;若收入不
变→a=0,人数增加→b>0,人均收入降低,即 a<b→平均数下降;若收入不变
→a=0,人数不变→b=0,相当于一切都不变,则人均收入也不变,即 a=b→平均
数不变。
3.a、b为增长率,无论正负,同样适用,带着符号比大小即可。
2023 年一季度,新疆金属矿及矿砂、未锻轧铜及铜材、煤炭分别进口 35.5
亿元、11.4 亿元、3.7 亿元,同比分别增长 134.1%、65.3%、79.6%,进口量同
比分别增长102.5%、69.4%、78.8%。同期,进口农产品15.2亿元,同比增长20.5%。
【例 1】(2024 联考)不能从上述资料中推出的是:
A.略
B.2023 年一季度,新疆煤炭进口单价高于上年同期水平
C.略
D.略
【解析】1.B 项:结合生活实际分析,单价=钱/量,“量”可能是重量,也
可能是个数,要想单价高于上年,则 a>b,由材料可知,钱的增速 a=79.6%,进
口量的增长率 b=78.8%,a>b→平均数上升,正确,本题问“不能推出”,即问
不对的选项,故不选。【不选】
【注意】
1.每篇资料分析的最后一道题(类似于答题),通常给出 4 个选项,要求判
断哪个选项是正确的、哪个选项是错误的,做起来会稍微费点时间,是 4个基础
小题的结合,一定要将基础知识弄扎实。
282.平均数的升降判断很难出单题,故往往在综合分析中以一个选项的形式进
行呈现。
2022 年,全国共有 260家银行机构和 29家理财公司累计新发理财产品2.94
万只,同比下降38.23%,降幅比上年同期扩大7.22个百分点;累计募集资金89.62
万亿元,同比减少 32.57万亿元。
【例 2】(2024 联考)能够从上述资料中推出的是:
A.略
B.2022 年新发理财产品中平均每只产品募集资金低于 2021 年
C.略
D.略
【解析】2.B 项:出现“平均每”,问“低于”,则找 a<b,平均数=后/前=
募集资金/新发理财产品,新发理财产品 b=-38.23%,募集资金 a没有直接给出,
只需要快速估算,根据公式:r=增长量/基期=增长量/(现期-增长量)≈-32.57/
(90+32.57)=-32+/122+=-20+%,具体数据不需要算出来,能比较大小即可。负
数比较,负得越多值越小,a>b→平均数上升,错误,不选。【不选】
【注意】
1.r=增长量/基期=增长量/(现期-增长量),增长量减少、是负值,需要带
上负号计算。
2.比去年少/低,根据高减低加可知去年更高。
3.平均数的增长量已经很多年没有考了,联考这么多年,仅在 2020 年考了
1 次,是最低频的考点,国考从来没考过。平均数的增长量=现期平均数- 基期
平均数,与两期比重差公式相同。
4.本题选什么不重要,重点是通过选项学习知识点。
三、两期平均——计算:平均数的增长率
识别:平均数+增长+%
例:2015年 1~5月B区规模以上文化创意产业从业人员人均收入约比上年
29同期增长:
A.2.5% B.8.4%
C.10.8% D.13.4%
公式:r=(a-b)/(1+b)(a是分子的增长率,b是分母的增长率)
做题逻辑:找 a、b代入公式,非常简单
【注意】
1.平均数是具体的值,如人均收入为 50万,可以求增长率。
2.识别:平均数+增长+%→平均数+增长率。
3.公式:r=(a-b)/(1+b),是唯一分母为“1+b”的公式。
4.例:人均收入+增长+%,为平均数的增长率问题,直接代入公式,r=(a-b)
/(1+b),a 为分子增长率,b 为分母增长率,找到 a 和 b,代入公式即可得分,
公式非常简洁,计算量几乎没有。
公式推导
现期平均:A/B 基期平均:A/B*[(1+b)/(1+a)]
平均数增长率=(现期- 基期)/基期
={A/B-A/B*[(1+b)/(1+a)]}÷{A/B*[(1+b)/(1+a)]}
=[1-(1+b)/(1+a)]÷[(1+b)/(1+a)]
=[1+a-(1+b)]/(1+b)
=(a-b)/(1+b)
【注意】平均数的增长率,公式非常简洁,推导不重要,记住公式即可。
2023 年前 5 个月,天津口岸出口汽车约 17.2 万辆,同比增长 29.5%,总价
值约100.1 亿元人民币,同比增长 40.2%。
【例 3】(2024 联考)2023年1~5月,天津口岸出口汽车均价同比上涨:
A.8% B.12%
C.16% D.20%
【解析】3.“均价”为平均数,“上涨”即上升,问平均数+上升+%,为平均
数的增长率问题,根据公式:r=(a-b)/(1+b),找到a和 b,代入公式即可得
30分。均价=钱/量,钱的增速为 a,量的增速为 b,由材料可知 a=40.2%,b=29.5%,
代入数据:(40.2%-29.5%)/(1+29.5%)=10.7%/1+<10.7%,仅 A项满足。【选A】
【注意】
1.确定分子、分母(谁除以谁);代入公式:r=(a-b)/(1+b),平均数的
增长率是套路、代公式的送分题,基本上没有什么计算量,判断分母比 1大或比
1小,找到答案的范围即可,不要有畏难情绪。
2.比重差问的是“上升/下降+百分点”,百分点是两个百分数作差;增长率
是两个数的比例关系。
2018 年前三季度,S省社会物流总额 35357.26亿元,同比增长6.4%,增速
比上半年放缓 0.7 个百分点。其中,工业品物流总额 16636.15 亿元,同比增长
0.2%,增速比上半年放缓 2.1 个百分点;外部流入(含进口)货物物流总额
17357.31亿元,同比增长 12.1%,增速比上半年加快 0.8个百分点;农产品物流
总额 875.06 亿元,同比增长 11.6%,增速比上半年加快 0.5 个百分点;单位与
居民物品物流总额 457.86 亿元,同比增长 40.7%,增速比上半年放缓 3 个百分
点;再生资源物流总额 30.88 亿元,同比下降 7.0%,降幅比上半年扩大 4.3 个
百分点。
2018 年前三季度,S省社会物流总费用 2682.1亿元,同比增长 6.3%,比上
半年放缓0.9个百分点。其中:物流运输环节总费用1854.6亿元,同比增长6.3%;
保管环节总费用 612.4 亿元,同比增长 6.4%;管理环节总费用 214.9 亿元,同
比增长6.4%。
【例 4】(2020 国考)2018 年前三季度,平均每万元社会物流总额产生的物
流费用比上年同期:
A.上升了不到 1% B.上升了1%以上
C.下降了不到 1% D.下降了1%以上
【解析】4.出现“平均每”,为平均数问题;问上升/下降+%,为增长率问题,
结合可知本题为平均数的增长率问题,根据公式:r=(a-b)/(1+b)。“产生”
是动词,不是主语,平均数=后/前=物流费用/社会物流总额,物流费用 a=6.3%,
31社会物流总额b=6.4%,代入数据:(6.3%-6.4%)/(1+6.4%)=-0.1%/(1+6.4%)
<0→下降,排除 A、B项;0.1%/1+<0.1%,C项当选。【选 C】
【注意】平均数的增长率,无脑套公式,根据“后/前”找到 a和b。
2017 年,A 省完成客运总量148339 万人次,同比增长 5.4%,增幅比前三季
度提高 0.2 个百分点,比上年提高 0.5 个百分点;完成旅客周转总量 4143.84
亿人公里,增长 7.7%,增幅比前三季度提高 0.7 个百分点,比上年提高 1.8 个
百分点。
【拓展练习】(2019国考)2017年前三季度,A省平均每人次客运旅客运输
距离(旅客周转量/客运总量)同比:
A.下降了不到 2% B.下降了2%以上
C.上升了不到 2% D.上升了2%以上
【解析】拓展.做资料分析题,最容易掉的是时间坑,问题时间为 2017年前
三季度,材料已知增长率为全年的数据,不能直接用,增幅就是增长率,“高”
则减,故 a=7.7%-0.7%=7%,b=5.4%-0.2%=5.2%,根据公式:r=(a-b)/(1+b)
=1.8%/(1+5.2%)=1.8%/1+<1.8%,C 项当选。【选C】
【注意】
1.有同学认为 a=7.7%、b=5.4%,直接代入公式:(7.7%-5.4%)/(1+5.4%),
因此误选D项。
2.可以先根据 a、b判升降,但没有意义,还是需要代入公式计算具体值。
3.增长率通过正负体现上升或下降,r>0→上升、r<0→下降。
4.平均数的增长率不能用“<|a-b|”秒杀,若b>0,则平均数的增长率<
a-b;若 b<0,则平均数的增长率>a-b,没有什么规律,直接代公式,简单计
算即可得分,并不难。
对比总结
【问法 1】(2021江苏)2019年保费收入占江苏省总保费收入比重同比增加
32的险种是:
【问法 2】(2018联考)2017年5 月,股份制商业银行总资产占银行业金融
机构的比重与上年相比约:
A.增加了 2 个百分点
【问法 3】(2022江苏)2021年上半年,我国集成电路出口平均价格同比有
所提高
【问法 4】(2019北京)2016年全社会餐饮业平均每个经营单位的从业人数
比上年约:
A.减少了 2% B.减少了15%
C.增加了 2% D.增加了15%
【注意】
1.问法 1:出现“比重”,为比重类问题;问“增加”,即上升,为比重上升
/下降,为两期比重升降判断或两期比重比较,a>b→比重上升,a<b→比重下
降,a=b→比重不变,是送分题。“同比”就是和去年相比。
2.问法 2:出现“比重”,问增加/减少+百分点,比重是百分数的形式,百
分数作差必须用百分点严谨表述,故为两期比重差计算问题,两步走,判断上升
或下降(a>b→比重上升,a<b→比重下降,a=b→比重不变);定大小,<|a-b|;
如果不行,就代公式,A/B*[(a-b)/(1+a)]。
3.问法 3:出现“平均”,问提高,问两期平均升降判断或两期平均比较,a
>b→平均数上升,a<b→平均数下降,a=b→平均数不变。
4.问法 4:出现“平均每”,问增加/减少+%,为平均数的增长率问题,没有
结论和技巧,直接套公式,r=(a-b)/(1+b)。
课后作业
33课后作业两件事
①复习:知识点填空,讲义题目独立过一遍,整理课堂笔记
②预习:202 页~212页(倍数和特殊增长率)
把题做一遍,有时间的同学可以自己尝试推导思维导图的公式
不求快,重要的是过程
明天晚上 6:55提前5分钟开课,一起回顾本节课知识点
明天最后会梳理资料分析所有重难点(考情、公式、技巧等)以及复习策略
【答案汇总】
比重:现期比重 1-5:BCBCD;基期比重 1-2:DA;两期比重 1-4:CCAA
平均数:现期平均数与基期平均数 1-4:CDBA;两期平均数 1-4:不选、不
选、AC
34遇见不一样的自己
Be your better self
35