文档内容
方法精讲-资料 4
(笔记)
主讲教师:张小飞
授课时间:2024.06.01
粉笔公考·官方微信方法精讲-资料 4(笔记)
【注意】资料 3课后作业:
1.比重,部分在总体中所占的比率;平均数,总数除以个数,后除以前。比
重的关键词是“占”字,平均数的关键词是“每、平均”,要记住题型特征。
2.现期比重公式:部分/总体;现期平均数公式:后/前。
3.基期比重公式(问题时间在前为基期时间):A/B*[(1+b)/(1+a)];基
期平均数公式:A/B*[(1+b)/(1+a)]。若选项差距大,可以截位直除,也可
以用第二种方法;若选项差距小,先算 A/B,再看(1+b)/(1+a)与 1的关系,
从而排除选项。
4.两期比重题型识别:题干中有两个时间,问题中有占、比重;两期平均数
题型识别:有两个时间,问题中有均、每、单位。比重和平均数的区别在于关键
词不同。
15.两期比重判升降:a>b,比重上升;a<b,比重下降;a=b,比重不变。a
→部分增长率,b→总体增长率。
6.两期平均数判升降:a>b,平均数上升;a<b,平均数下降;a=b,平均
数不变。a→分子增长率,b→分母增长率。平均数=后(a)/前(b)。
7.两期比重差计算公式:若无法根据“两期比重差<|a-b|”确定最终答案,
需要代入公式计算,A/B*[(a-b)/(1+a)]。
8.平均数增长率题型识别:平均数增长/下降+%;计算公式:(a-b)/(1+b)。
目录
第七节 倍数
第八节 特殊增长率
第九节 广东特色直接找数
【注意】本节课讲解倍数、特殊增长率和广东特色找数问题(看似是 2024
年新增加的模块,但之前也涉及过,是很简单的题目)
资料分析 方法精讲 4
学习任务:
1.课程内容:倍数、特殊增长率、广东特色直接找数
2.授课时长:3小时
3.对应讲义:第 158~171页
4.重点内容:
(1)倍数与增长率的相互转化
(2)间隔增长率的对应公式
(3)年均增长率的比较技巧
(4)混合增长率的两个结论
(5)广东特色直接找数的解题思维
第七节 倍数
基本术语:
2倍数用来表示两个量的相对关系。
A是 B的n倍:n=A/B。
A比 B增长(多)r倍:r=A/B-1。
一、现期倍数
二、基期倍数
【注意】倍数:考查较少,难度较低,问 A 是 B 的几倍→A/B;A 与 B 之比
为多少→A/B,两者含义相同,根据时间不同分为现期倍数和基期倍数。比重问
题也分为现期比重和基期比重;平均数问题也分为现期平均数和基期平均数,问
题时间相同为现期,,问题时间在前为基期问题,两期倍数几乎没有涉及过,但
如果考查也要会,要学会举一反三,若两期倍数判断升降,问 2021 年 a 是 b 的
倍数与 2020 年相比上升还是下降,找分子增长率(a)、分母增长率(b),若 a
>b→上升,a<b→下降,a=b→不变,若问两期倍数升降判断,与两期比重、两
期平均数的升降判断一致,只是考查较少,如果考查到也能应对。
一、现期倍数
题型识别:问题时间与材料一致+倍、比
计算公式:
(1)A是B的几倍、A与B之比是几倍=A/B
500 元是100元的多少倍?
(2)A比B多/增长/高几倍多几倍=r=A/B-1
500 元比100元多几倍?
(3)A超过B 的N倍A>B*N
201 元是否超过 100元的2倍?
速算技巧:截位直除
【解析】现期倍数:
1.题型识别:问题时间与材料一致+倍、比。
2.计算公式:
(1)A是B的几倍、A与B之比。
3①是几倍=A/B。
②500 元是100 元的多少倍?500元是 100元的5倍。
(2)A比B多/增长/高几倍。
①多几倍=r=A/B-1。
②500 元比100 元多几倍?500元比100 元多400元,400元/100 元=4倍,
故500元比 100元多 4倍,或500/100-1=5-1=4。故多几倍=是几倍-1,多几倍=
增长率。增长率=是几倍-1,如200元比100 元多1倍,200元比100元增长 100%,
100%=1,因此多几倍=增长率=是几倍-1,此处常常会挖坑,没有看到问的是多几
倍,而习惯性的认为是几倍,忘记“-1”,会掉“坑”,不仅模考喜欢这样设置
选项,真题也会这样设置选项,所有的模考题目都是参考真题设置的。
(3)A超过B 的N倍。资料分析的题干中出现超过就是“>”的意思。
①A>B*N。
②201 元是否超过 100元的2倍?
答:超过→>,201 元>100*2=200 元,201 元超过 100 元的 2 倍。超过 2
倍→>2 倍,但大于 2倍不一定是3倍,2.01 倍是大于2倍,2.00001 倍也是大
于2倍的意思。
3.速算技巧:截位直除。
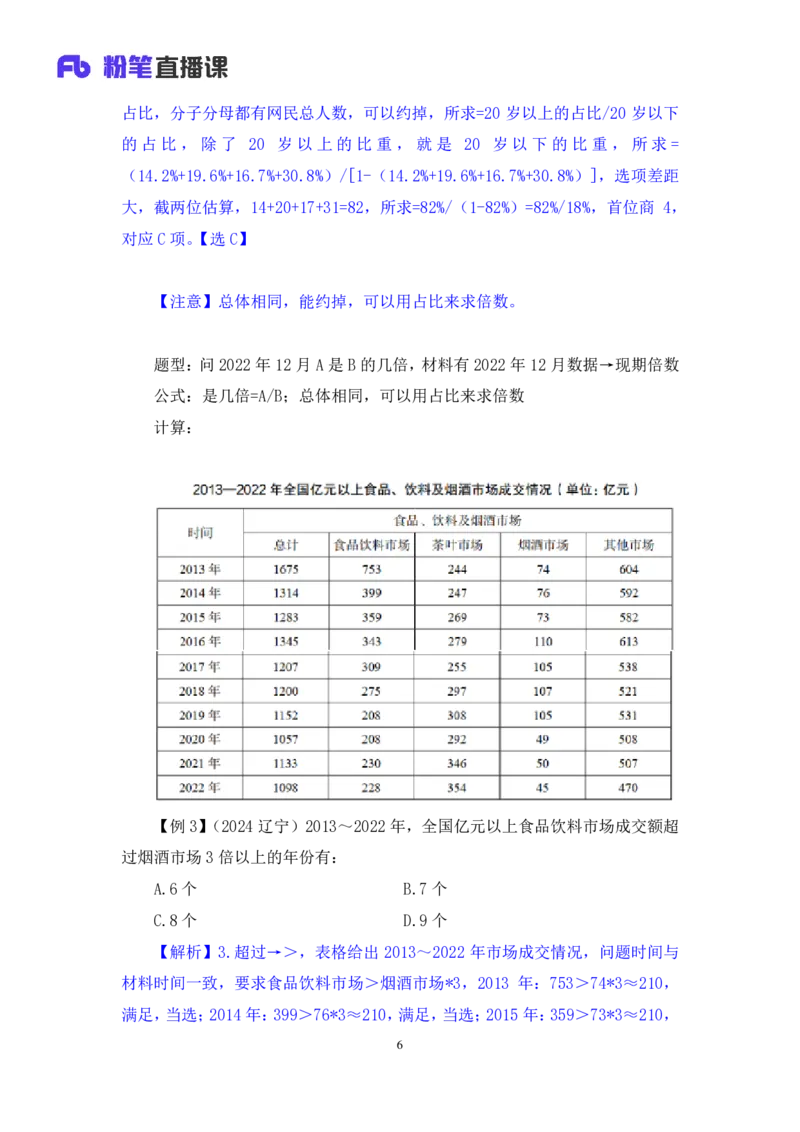
4【例 1】(2023 广东)2021年广东农林牧渔业总产值约为 9年前的多少倍?
A.1.2 B.1.4
C.1.6 D.1.8
【解析】1.为→是,问倍数,2021年的 9年前为2021-9=2012年,已知 2012
和2021 年的数据,材料给的时间和问题时间相同,为现期倍数,找到两个数据,
所求=2021 年/2012 年=8305.8/4550.3,观察选项,选项差距大(首位相同,次
位差>首位),截两位,原式转化为 8305.8/46,首位商1,次位商8,对应D项。
【选D】
题型:问 2021 是9年前的几倍,材料有 2012~2021数据→现期倍数
公式:是几倍=A/B
计算:
2022 年 12 月,20~29 岁、30~39 岁、40~49 岁网民占比分别为 14.2%、
19.6%和16.7%;50岁及以上网民群体占比由2021年12月的26.8%提升至30.8%,
互联网进一步向中老年群体渗透。
【例 2】(2024 贵州)截至 2022 年 12 月,我国 20 岁以上网民人数是 20 岁
以下网民人数的:
A.不到 3倍 B.3~4倍之间
C.4~5倍之间 D.5 倍以上
【解析】2.材料时间为 2022年12月,问题时间为 2022年12月,问题时间
与材料时间一致,为现期问题,问是几倍,为现期倍数问题,找到 20 岁以上的
网民人数,和20岁以下的网民人数做除法即可,定位材料找数据,占比→比重,
“50岁及以上网民群体占比由 2021年12月的 26.8%提升至30.8%”,故 2022年
12月50 岁以上的占比为 30.8%(考查基本对文字的理解能力)。
没有给出具体数值,给出的都是占比,要求网民人数,要根据占比求解,比
重=部分/总体,材料中给出的比重是 20 岁占网民总人数的比重,则任何一个年
龄段的人数都是网民总人数的一部分,部分量=总体*比重,故20岁以上的人数=
网民总人数*20 岁以上的占比,20 岁以下网民的人数=网民总人数*20 岁以下的
5占比,分子分母都有网民总人数,可以约掉,所求=20 岁以上的占比/20 岁以下
的占比,除了 20 岁以上的比重,就是 20 岁以下的比重,所求=
(14.2%+19.6%+16.7%+30.8%)/[1-(14.2%+19.6%+16.7%+30.8%)],选项差距
大,截两位估算,14+20+17+31=82,所求=82%/(1-82%)=82%/18%,首位商 4,
对应C项。【选 C】
【注意】总体相同,能约掉,可以用占比来求倍数。
题型:问2022 年12月A是B的几倍,材料有 2022年12月数据→现期倍数
公式:是几倍=A/B;总体相同,可以用占比来求倍数
计算:
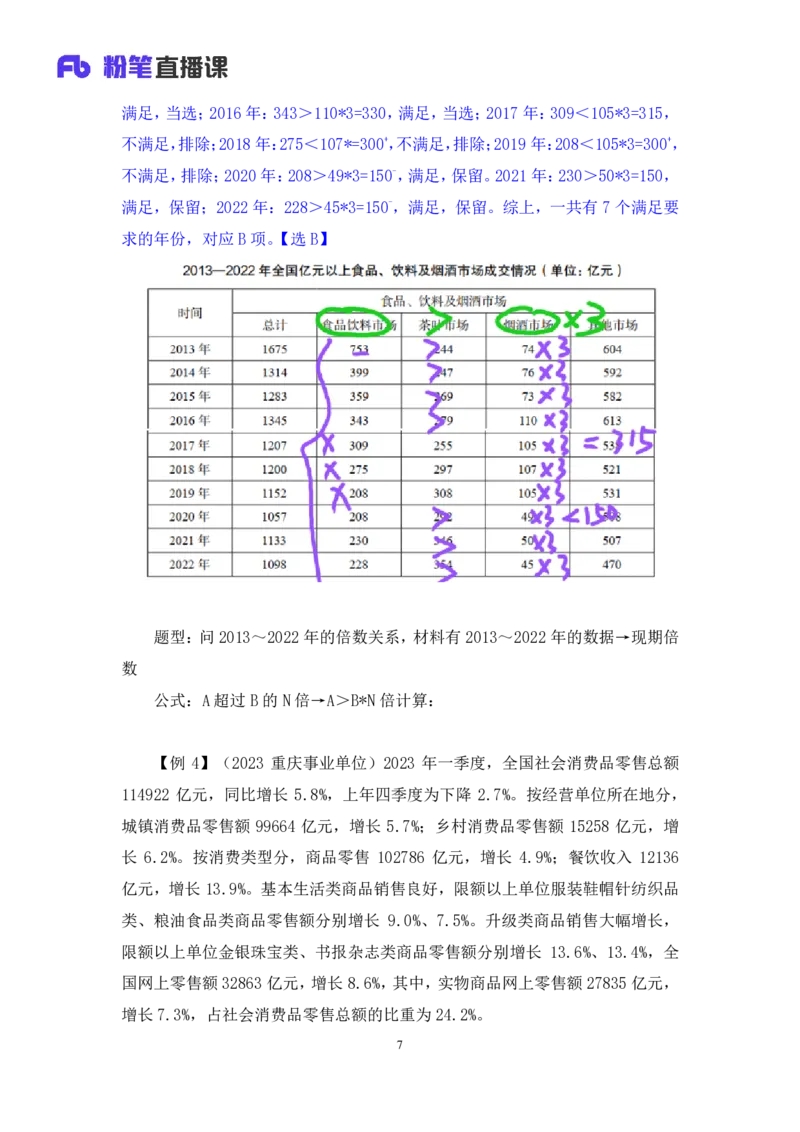
【例 3】(2024 辽宁)2013~2022年,全国亿元以上食品饮料市场成交额超
过烟酒市场3倍以上的年份有:
A.6 个 B.7 个
C.8 个 D.9 个
【解析】3.超过→>,表格给出 2013~2022 年市场成交情况,问题时间与
材料时间一致,要求食品饮料市场>烟酒市场*3,2013 年:753>74*3≈210,
满足,当选;2014年:399>76*3≈210,满足,当选;2015年:359>73*3≈210,
6满足,当选;2016年:343>110*3=330,满足,当选;2017年:309<105*3=315,
不满足,排除;2018 年:275<107*=300+,不满足,排除;2019年:208<105*3=300+,
不满足,排除;2020 年:208>49*3=150-,满足,保留。2021年:230>50*3=150,
满足,保留;2022 年:228>45*3=150-,满足,保留。综上,一共有 7个满足要
求的年份,对应B 项。【选B】
题型:问2013~2022年的倍数关系,材料有 2013~2022年的数据→现期倍
数
公式:A超过 B的N倍→A>B*N倍计算:
【例 4】(2023 重庆事业单位)2023 年一季度,全国社会消费品零售总额
114922 亿元,同比增长 5.8%,上年四季度为下降 2.7%。按经营单位所在地分,
城镇消费品零售额 99664 亿元,增长 5.7%;乡村消费品零售额 15258 亿元,增
长 6.2%。按消费类型分,商品零售 102786 亿元,增长 4.9%;餐饮收入 12136
亿元,增长13.9%。基本生活类商品销售良好,限额以上单位服装鞋帽针纺织品
类、粮油食品类商品零售额分别增长 9.0%、7.5%。升级类商品销售大幅增长,
限额以上单位金银珠宝类、书报杂志类商品零售额分别增长 13.6%、13.4%,全
国网上零售额32863 亿元,增长8.6%,其中,实物商品网上零售额 27835 亿元,
增长7.3%,占社会消费品零售总额的比重为 24.2%。
7按经营单位所在地分,2023 年一季度,城镇消费品零售额约比乡村消费品
零售额多多少倍?
A.4.5 B.5.5
C.6.5 D.7.5
【解析】4.多几倍=是几倍-1,观察选项,相邻两项之间相差 1,只要忘记
“-1”,就会掉“坑”,问题时间与材料时间一致,为现期倍数,定位材料找数据,
所求=99664/15258-1,选项首位不同,计算出首位即可,99664/15258,首位商
6,商不到7,所求=6+-1=5+,对应B项。【选 B】
题型识别:问题时间在材料之前+倍、比
计算公式:基期倍数=A/B*[(1+b)/(1+a)]
A:分子的现期量 B:分母的现期量
a:分子的增长率 b:分母的增长率※增长率要带着正负号
速算技巧:1.截位直除(选项差距大)
2.先算 A/B,再看(1+b)/(1+a)与 1的关系,从而排除选项。
【注意】基期倍数:
1.题型识别:问题时间在材料之前+倍、比。
2.计算公式:
(1)基期倍数=A/B*[(1+b)/(1+a)]。
(2)A:分子的现期量、B:分母的现期量;a:分子的增长率、b:分母的
增长率。
(3)增长率要带着正负号。
3.速算技巧:
(1)截位直除(选项差距大)。
(2)先算A/B,再看(1+b)/(1+a)与 1的关系,从而排除选项。
【例 5】(2024 浙江)2023 年第 14 周,H 市哨点医院共报告流感样病例总
数为 5187 例,比上周增加 4.49%,比去年同期减少 56.16%,其中国家级哨点医
院455例,比上周减少 6.57%,比去年同期减少 55.04%。城区哨点医院 1899例,
8比上周减少 19.40%,比去年同期减少 55.46%;郊区、县(市)哨点医院 3288
例,比上周增加26.07%,比去年同期减少56.55%。本周全市哨点医院ILI%为5.98%,
比上周低 0.07 个百分点,其中国家级哨点医院 ILI%为 2.12%,比上周高 0.23
个百分点。城区哨点医院 ILI%为4.45%,比上周低 0.56个百分点;郊区、县(市)
哨点医院ILI%为7.46%,比上周高0.01个百分点。
2023 年第 13 周,H 市郊区、县(市)哨点医院报告流感样病例约是城区的
多少倍?
A.1.7 B.1.5
C.1.3 D.1.1
【解析】5.问题时间为 2023年第13周,材料时间为 2023年第 14周,问题
时间靠前,为基期时间,问倍数,为基期倍数问题,找到数据套公式即可,“城
区哨点医院1899例,比上周减少 19.40%,比去年同期减少 55.46%;郊区、县(市)
哨点医院 3288 例,比上周增加 26.07%,比去年同期减少 56.55%”,注意要用比
上周的增长率(14 周和 13 周差一周),减少 19.40%→r=-19.40%,所求
=3288/1899*[(1-19.4%)/(1+26.07%)],选项差距大(次位差>首位),且选
项之间没有十倍、百倍的差距,可以截两位直除,原式转化为 33/19*81/13,此
时不好约分,可以选择一个数据进行“+1、-1”微调,目的是微调后要好算,令
19-1=18,原式转化为 33/18*81/13=33*9/26=297/26,首位商 1,次位商 1,对
应D项。【选 D】
【注意】尽量对一个数据进行微调,若进行微调的数据越多,误差就越大。
9【注意】倍数:
1.超过→>。
2.基期倍数与基期比重、基期平均数是一个套路。
第八节 特殊增长率
一、间隔增长率
二、年均增长率
三、混合增长率
【注意】特殊增长率:间隔增长率、年均增长率、混合增长率,年均增长率
结束会休息。
一、间隔增长率
题型识别:中间隔一个时期(一般隔 1 年),求增长率
某企业 2023年主营业务收入同比增长率为 r,2022年同比增长率为 r。问
1 2
该企业2023年主营业务收入比 2021年增长百分之多少?
【注意】间隔增长率:题型的名字不是出题人取的,是培训机构取的名字,
名字的后缀有“增长率”,说明本质上是求增长率的,需要出现“增长+%”,“间
隔”体现在中间会间隔一个时期,一般是间隔一年,问增长率,中间间隔一个时
期为间隔增长率问题。
1.题型识别:中间隔一个时期(一般隔 1年),求增长率。
2.例.某企业 2023 年主营业务收入同比增长率为 r,2022 年同比增长率为
1
r。问该企业2023 年主营业务收入比2021 年增长百分之多少?
2
(1)增长+%→增长率,2023年与2021 年中间间隔2022年,为间隔增长率。
也有同学称为笑脸公式,给出 2023 年比 2022 年的增长率为 r,给出 2022 年比
1
2021年的增长率为 r,问2023年比2021年增长了百分之多少,为 r 。画出这
2 间
10个时间区间,刚好为一个笑脸。
(2)公式推导:假设 2021 年的工资为 A万元,2022年与2021 年相比,则
2022 年为现期,2022 年=A*(1+r),2022 年是 2023 年的基期,则 2023 年=A*
2
(1+r)*(1+r),r=(现期量- 基期量)/基期量,问题时间为2023 年和2021
2 1
年,问题时间靠后的2023年为现期,问题时间靠前的2021年为基期,r=[A*(1+r)
2
*(1+r )-A]/A=(1+r )*(1+r )-1=r+r +r *r 。推导过程了解即可,重点是
1 2 1 1 2 1 2
结论。
3.公式:r =r +r+r*r=和+积。
间 1 2 1 2
4.2021年的增长率是与2020年相比的,而题目中问的是2021年和2023年,
故通过2022年将2021 年与2023年连在一起即可,不需要与 2020年链接,故不
需要知道2021年的同比增长率。
1.r 、r 怎么找→r、r 为r 、r
1 2 1 2 今 去
【1】2019年比 2017年增长率百分之多少?
r、r 为:
1 2
【2】2016年比 2014年增长了百分之多少?
r、r 为:
1 2
2.怎么算
(1)先算加法:结合选项排除
(2)再算乘法:
①若|r|、|r |均小于10%,|r*r|<1%,一般可以忽略
1 2 1 2
②有超过 10%,一个不变,另一个百化分/小数
11【1】8.5%+36%+8.5%*36%≈
A.47.6% B.40.4%
C.34.5% D.27.6%
【2】5.3%+(-1%)+5.3%*(-1%)≈
A.1.8% B.4.2%
C.6.3% D.9.6%
【3】11.6%+20.4%+11.6%*20.4%≈
A.33.6% B.34.4%
C.32.0% D.31.2%
【注意】
1.r 、r 怎么找→r、r 为 r 、r ,r =r+r+r*r,乘法与加法之间存在
1 2 1 2 今 去 间 1 2 1 2
交换律,因此谁是 r、谁是r 不重要。
1 2
(1)2019年比 2017年增长率百分之多少?
答:用今年 2019 年(29%)和去年2018 年(28%)的数据。
(2)2016年比 2014年增长了百分之多少?
答:用今年 2016 年(26%)和去年2015 年(25%)的数据。
2.怎么算:
(1)先算加法:精确计算,看是否能排除三个选项,结合选项排除。
(2)再算乘法:
①若|r|、|r|均小于10%,则|r*r|<1%(若r、r 均为10%,10%*10%=1%),
1 2 1 2 1 2
一般可以忽略。
②有超过 10%,一个不变,另一个百化分/小数。
(3)例:
①8.5%+36%+8.5%*36%≈
A.47.6% B.40.4%
C.34.5% D.27.6%
答:8.5%*36%=正数,原式=44.5%+正数>44.5%,排除 B、C、D 项,选择 A
项。
②5.3%+(-1%)+5.3%*(-1%)≈
12A.1.8% B.4.2%
C.6.3% D.9.6%
答:原式=4.3%+负数<4.3%,能排除 C、D 项,两个增长率的绝对值均小于
10%,故乘积的绝对值一定小于 1%,所求比 4.3%小,但不会超过1个百分点,对
应B项。
③11.6%+20.4%+11.6%*20.4%≈
A.33.6% B.34.4%
C.32.0% D.31.2%
答:原式=32%+正数>32%,排除C、D项;r、r 均超过10%,乘积不能忽略,
1 2
20.4%≈1/5,11.6%*(1/5)≈2.3%,32%+2.3%≈34.3%,对应B项。
一、间隔增长率
题型识别:中间隔一个时期(一般隔 1 年),求增长率
计算公式:r =r+r+r*r
间 1 2 1 2
速算技巧:
(1)先算加法:结合选项排除
(2)再算乘法:
①若|r|、|r |均小于10%,|r*r|<1%,一般可以忽略
1 2 1 2
②有超过 10%,一个不变,另一个百化分/小数
【注意】间隔增长率:
1.题型识别:中间隔一个时期(一般隔 1年),求增长率。
2.计算公式:r =r+r+r*r。r、r 是今年和去年的增长率与前年的增长率
间 1 2 1 2 1 2
无关。
3.速算技巧:
(1)先算加法:结合选项排除。
(2)再算乘法:
①若|r|、|r |均小于10%,|r*r|<1%,一般可以忽略。
1 2 1 2
②有超过 10%,一个不变,另一个百化分/小数。
4.如给出 2021 年 r=10%、2022 年 r=12%、2023 年 r=13%、2024 年 r=14%,
13问 2024 年比 2021 年增长了百分之多少。此时先利用 2022、2023、2024 年计算
出2024 年比2022 年的间隔增长率;已知2022 年比2021年的增长率,再用间隔
增长率,求出2024 年比2021年的增长率。但这种情况考查较少。
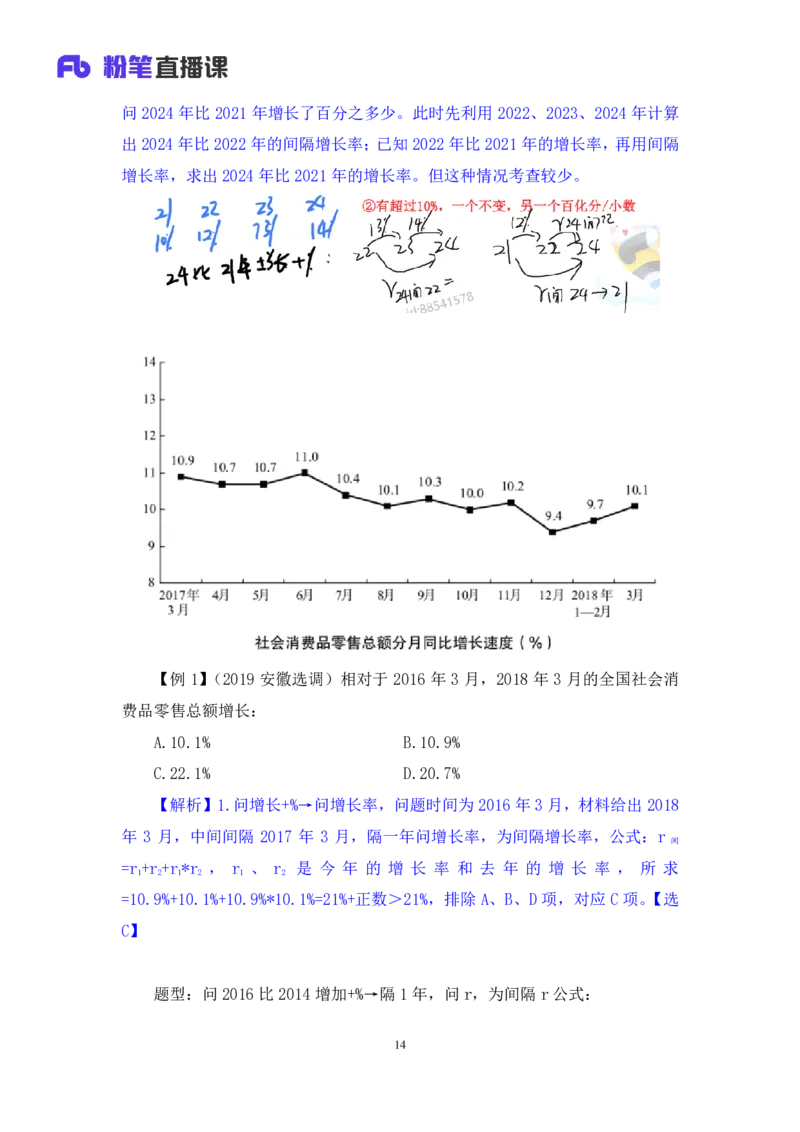
【例 1】(2019 安徽选调)相对于 2016 年 3 月,2018 年 3 月的全国社会消
费品零售总额增长:
A.10.1% B.10.9%
C.22.1% D.20.7%
【解析】1.问增长+%→问增长率,问题时间为 2016年3月,材料给出 2018
年 3 月,中间间隔 2017 年 3 月,隔一年问增长率,为间隔增长率,公式:r
间
=r+r+r *r , r 、 r 是 今 年 的 增 长 率 和 去 年 的 增 长 率 , 所 求
1 2 1 2 1 2
=10.9%+10.1%+10.9%*10.1%=21%+正数>21%,排除 A、B、D 项,对应 C 项。【选
C】
题型:问 2016 比2014增加+%→隔1年,问 r,为间隔r公式:
14计算:r =r+r +r*r
间 1 2 1 2
2022 年,全国软件和信息技术服务业规模以上企业超 3.5 万家,累计完成
软件业务收入 108126 亿元,同比增长 11.2%,增速较上年同期回落 6.5 个百分
点。
【例 2】(2024 四川)2022 年,全国软件和信息技术服务业规模以上企业累
计完成软件业务收入约比 2020年增长了:
A.16% B.23%
C.29% D.31%
【解析】2.增长+%→增长率,2022年与 2020年中间隔了一年,为间隔增长
率问题,定位材料找数据,2022 年 r=11.2%,没有直接给出 2021 年 r,需要计
算,“增速较上年同期回落 6.5个百分点”,2022年的上年为2021年,要根据百
分点求百分数,高减低加,回落→降低,降低需要做加法,2021 年
r=11.2%+6.5%=17.7%,r =r+r+r*r=11.2%+17.7%+乘积=28.9%+正数>28.9%,
间 1 2 1 2
排除 C、D 项,计算乘积需要百化分,11.2%≈1/9,17.7%≈18%,18%/9=2%,所
求≈28.9%+2%=30.9%,对应D项。【选D】
题型延伸 1:间隔倍数
特征:间隔一年,求倍数
2020 年工资同比增长 10%,增速比去年提高 1个百分点。
问:2020年工资是 2018年的几倍
方法:1.先求 r
间
2.间隔倍数=r +1
间
【注意】题型延伸 1:间隔倍数。
1.特征:间隔一年,求倍数。
2.例:2020 年工资同比增长 10%,增速比去年提高 1 个百分点;问:2020
年工资是2018年的几倍?
答:所求=2020 年/2018 年,若题干中没有给出 2020 年和 2018 年的工资,
隔了一年问倍数,为间隔倍数问题,两步走,先求间隔增长率,“增速比去年提
15高 1 个 百 分 点 ”, 高 减 低 加 , 2019 年 r=10%-1%=9% , r
间
=r+r+r *r=10%+9%+10%*9%=19.9% , 是 几 倍 = 增 长 率 +1 , 间 隔 倍 数
1 2 1 2
=19.9%+1=1.199≈1.2倍。
3.方法:
(1)先求r 。
间
(2)间隔倍数=r +1。
间
题型延伸 2:间隔基期量
特征:间隔一年,求基期量
2020 年工资8000 元,同比增长10%,增速比去年提高 1个百分点。
问:2018年工资是多少元?
方法:
1.先求 r
间
2.间隔基期量=现期量/(1+r )
间
【注意】题型延伸 2:间隔基期量。
1.特征:间隔一年,求基期量。
2.例:2020 年工资 8000 元,同比增长 10%,增速比去年提高 1 个百分点。
问:2018 年工资是多少元?
答:2018 年时间靠前为基期,2018 年与 2020 年中间间隔 2019 年,间隔一
年问基期量,为间隔基期量。先求间隔增长率,基期=现期/(1+r ),计算量较
间
大,但不至于放弃,“增速比去年提高 1个百分点”,高减低加,去年的增长率为
9%,r =19.9%,2020 年比2018年增长率19.9%,所求=现期量/(1+r )=8000/
间 间
(1+19.9%)≈8000/1.2。
3.方法:
(1)先求r 。
间
(2)间隔基期量=现期量/(1+r )。
间
2018 年全年H 市保费收入65.4亿元,同比增长 0.7%。其中,寿险业务保费
收入39.5 亿元,下降 5.1%;健康和意外险业务保费收入 9.1亿元,增长 21.6%,
16增速同比增加5个百分点;财产险业务保费收入 3.4亿元,增长25.2%;车险业
务保费收入 13.3 亿元,增长 1.8%。全年支付各类赔款及给付 21.2 亿元,增长
5.3%。其中,寿险业务保费赔付 11.0亿元,增长 1.4%;健康和意外险业务保费
赔付3.0 亿元,增长 68.7%;财产险业务保费赔付 0.9亿元,增长5.7%;车险业
务保费赔付6.4亿元,下降 5.0%。
【例 3】(2021 新疆兵团)2016年全年 H市健康和意外险业务保费收入约为
多少亿元?
A.7.5 B.6.9
C.6.4 D.6.1
【解析】3.问题时间为 2016年,材料时间为 2018年,问题时间靠前为基期
时间,中间间隔2017 年,为间隔基期问题,定位材料找数据,“健康和意外险业
务保费收入9.1亿元,(同比)增长 21.6%,增速同比增加 5个百分点”,同比是
与 2017 年相比,高减低加,故 2017 年 r=21.6%-5%=16.6%,r =r+r +r*r,乘
间 1 2 1 2
积无法忽略(后续还要计算基期量),直接进行百化分,16.6%≈1/6,r
间
=21.6%+16.6%+21.6%*(1/6)=38.2%+3.6%=41.8%,间隔基期量=现期量/(1+r )
间
=9.1/1.418,选项差距小,需要截三位,原式转化为 9.1/1.42,看到 1.418 可
以百化分,14.3%≈1/7,142与143非常接近,原式转化为 9.1%*7,结果的有效
数字为637,对应 C项。【选C】
二、年均增长率
题型识别:年均增长最快,年均增长排序;年均增长+%
2020 年某公司产值为 A万元,2023年为 B万元。问该公司2021~2023年的
年均增长率为多少?
计算公式:(1+r)n=现期量/基期量(n 为年份差)
速算技巧:比较:n相同,直接比较现期量/基期量
【注意】年均增长率:比较喜欢考查比较类问题。
1.题型识别:年均增长最快,年均增长排序,为年均增长率的比较;年均增
长+%,为计算年均增长率。
2.公式推导:例.2020年某公司产值为 A万元,2023年为B万元。问该公司
172021~2023 年的年均增长率为多少?
答:实际情况下每个年份的增长率都不相同,若求年均增长率,是假定这个
时间段中每年的年均增长率均相同,2020年=A,2021年=A*(1+r)、2022 年=A*
(1+r)*(1+r)、2023年=A*(1+r)*(1+r)*(1+r)=A*(1+r)³=B→(1+r)
³=B/A,3表示的是年份差(2023-2020=3,与年均增长量中的年份差相同)。
3.计算公式:(1+r)n=现期量/基期量,n为年份差。
4.速算技巧:比较类题目,n相同,可以消掉相同的东西,直接比较“现期
量/基期量”,“现期量/基期量”越大,年均增长率越大,与一般增长率的比较相
同(除了基期年份不同)。
18【例 1】(2021 联考)2009~2019年,城镇私营单位平均工资年均增长率最
高的是:
A.科学研究、技术服务和地质勘查业
B.信息传输、计算机服务和软件业
C.金融业
D.建筑业
【解析】1.问年均增长率最高的,比较年均增长率的大小,没有特殊情况,
也没有五年规划,则 2009 年为基期,2019 年为现期,年份差相同
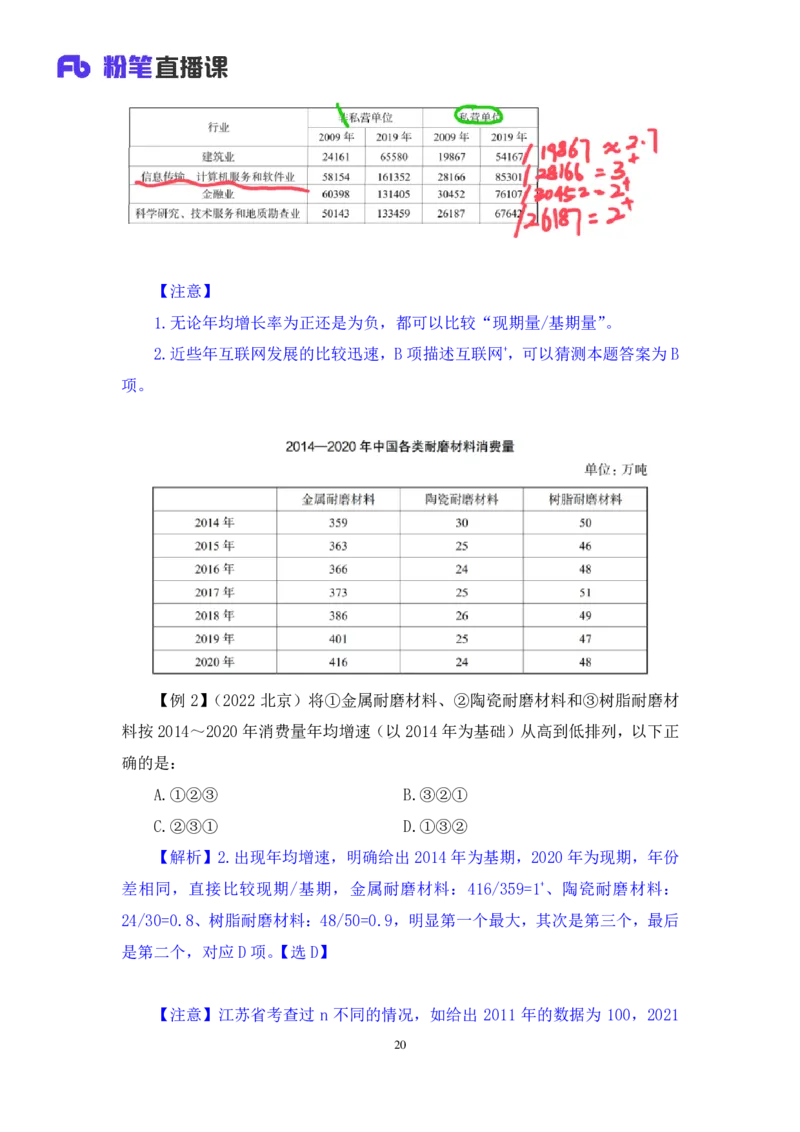
(n=2019-2009=10),直接比较现期/基期,现期/基期越大,则年均增长率越大,
问私营单位,注意不要找错数据,建筑业:54167/19867≈2.7(2+),信息传输、
计算机服务和软件业:85301/28166=3+、金融业:76107/30452=2+、科学研究、
技术服务和地质勘查业:67642/26187=2+,信息传输、计算机服务和软件业的倍
数关系最大,对应 B项。【选B】
19【注意】
1.无论年均增长率为正还是为负,都可以比较“现期量/基期量”。
2.近些年互联网发展的比较迅速,B项描述互联网+,可以猜测本题答案为 B
项。
【例 2】(2022 北京)将①金属耐磨材料、②陶瓷耐磨材料和③树脂耐磨材
料按2014~2020年消费量年均增速(以 2014 年为基础)从高到低排列,以下正
确的是:
A.①②③ B.③②①
C.②③① D.①③②
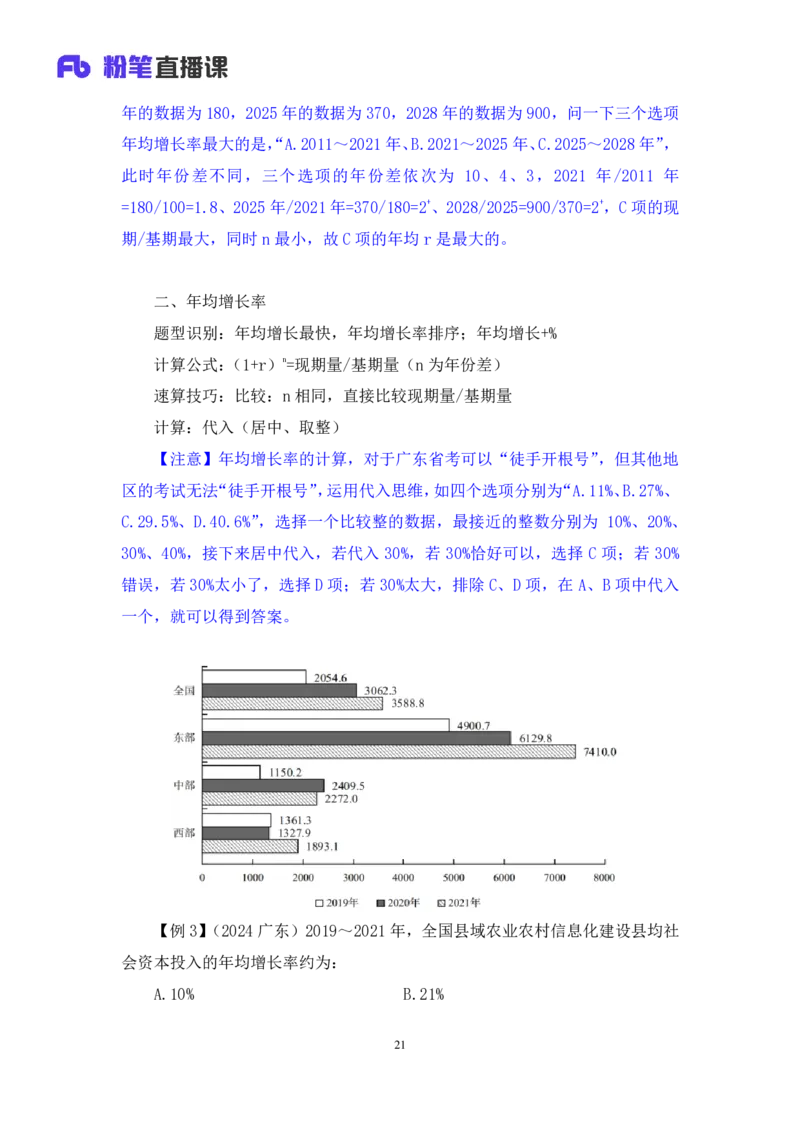
【解析】2.出现年均增速,明确给出 2014 年为基期,2020年为现期,年份
差相同,直接比较现期/基期,金属耐磨材料:416/359=1+、陶瓷耐磨材料:
24/30=0.8、树脂耐磨材料:48/50=0.9,明显第一个最大,其次是第三个,最后
是第二个,对应D 项。【选D】
【注意】江苏省考查过 n 不同的情况,如给出 2011 年的数据为 100,2021
20年的数据为180,2025 年的数据为370,2028 年的数据为900,问一下三个选项
年均增长率最大的是,“A.2011~2021年、B.2021~2025年、C.2025~2028年”,
此时年份差不同,三个选项的年份差依次为 10、4、3,2021 年/2011 年
=180/100=1.8、2025 年/2021年=370/180=2+、2028/2025=900/370=2+,C项的现
期/基期最大,同时 n最小,故C项的年均 r是最大的。
二、年均增长率
题型识别:年均增长最快,年均增长率排序;年均增长+%
计算公式:(1+r)n=现期量/基期量(n 为年份差)
速算技巧:比较:n相同,直接比较现期量/基期量
计算:代入(居中、取整)
【注意】年均增长率的计算,对于广东省考可以“徒手开根号”,但其他地
区的考试无法“徒手开根号”,运用代入思维,如四个选项分别为“A.11%、B.27%、
C.29.5%、D.40.6%”,选择一个比较整的数据,最接近的整数分别为 10%、20%、
30%、40%,接下来居中代入,若代入 30%,若 30%恰好可以,选择 C 项;若 30%
错误,若 30%太小了,选择 D 项;若 30%太大,排除 C、D 项,在 A、B 项中代入
一个,就可以得到答案。
【例 3】(2024 广东)2019~2021年,全国县域农业农村信息化建设县均社
会资本投入的年均增长率约为:
A.10% B.21%
21C.32% D.43%
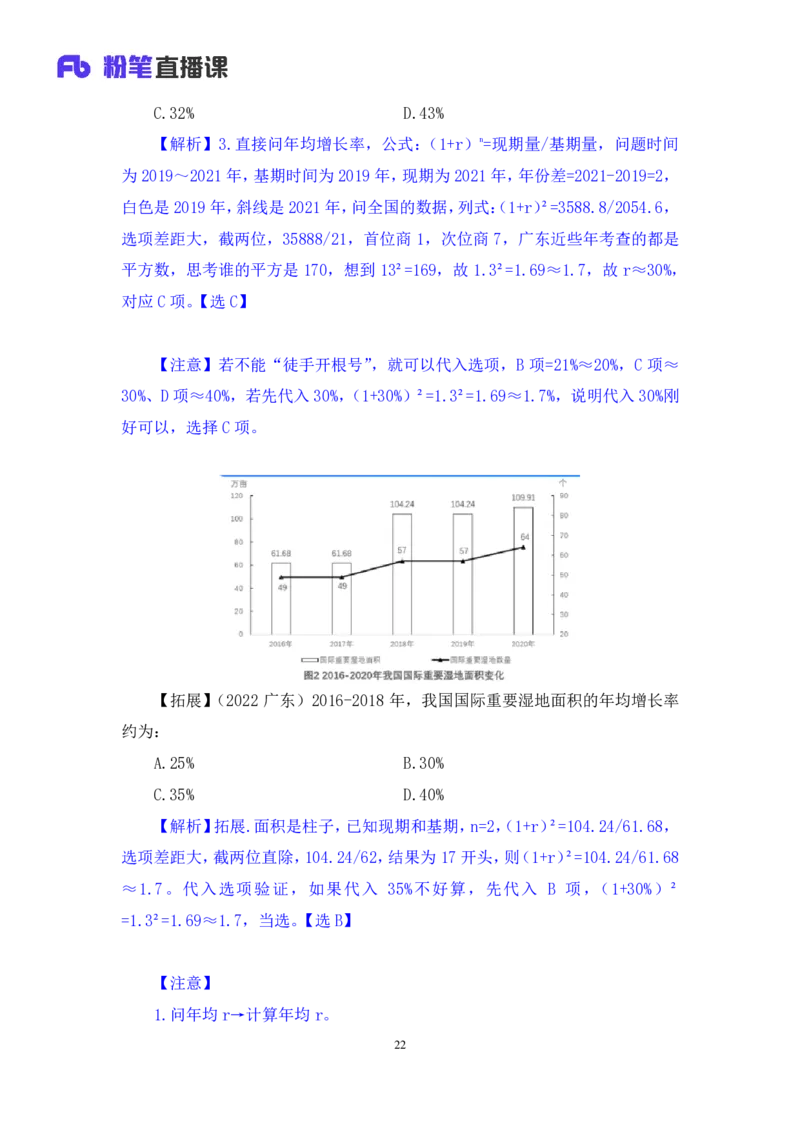
【解析】3.直接问年均增长率,公式:(1+r)n=现期量/基期量,问题时间
为2019~2021年,基期时间为 2019年,现期为 2021年,年份差=2021-2019=2,
白色是2019年,斜线是 2021年,问全国的数据,列式:(1+r)²=3588.8/2054.6,
选项差距大,截两位,35888/21,首位商 1,次位商 7,广东近些年考查的都是
平方数,思考谁的平方是 170,想到 13²=169,故 1.3²=1.69≈1.7,故 r≈30%,
对应C项。【选 C】
【注意】若不能“徒手开根号”,就可以代入选项,B 项=21%≈20%,C 项≈
30%、D项≈40%,若先代入 30%,(1+30%)²=1.3²=1.69≈1.7%,说明代入 30%刚
好可以,选择C项。
【拓展】(2022 广东)2016-2018 年,我国国际重要湿地面积的年均增长率
约为:
A.25% B.30%
C.35% D.40%
【解析】拓展.面积是柱子,已知现期和基期,n=2,(1+r)²=104.24/61.68,
选项差距大,截两位直除,104.24/62,结果为 17开头,则(1+r)²=104.24/61.68
≈1.7。代入选项验证,如果代入 35%不好算,先代入 B 项,(1+30%)²
=1.3²=1.69≈1.7,当选。【选 B】
【注意】
1.问年均 r→计算年均 r。
222.公式:(1+r)n=现期量/基期量,代入。
三、混合增长率
题型识别:部分与总体之间的增长率关系
本质:量之间为加和关系,则 r为混合。
例:2022年,A省进出口额为2000亿元。其中,进口 1500亿元,同比增长
15%;出口 500亿元,同比增长 20%。
2022 年A省进出口总额的同比增长率为:
例如:
①固定搭配:房产+地产=房地产、进口+出口=进出口、城镇+农村=全国、博
士+硕士=研究生、邮政+电信=邮电
②时间累计型:上半年+下半年=全年、一季度+二季度=上半年
③逻辑型:A+非A=全部(税收收入+非税收收入=总收入、规模以上+规模以
下=整体)。
方法:1.口诀:①总体 r居中但不正中(最小 r<总体r<最大 r)
【1】2020年进口额增长了 10%,出口额增长了 20%,则2020年进出口额可
能增长了:
A.8% B.9%
C.14% D.21%
形式:部分在两边,总体在中间
【注意】混合增长率:
1.题型识别:部分与总体之间的增长率关系。
2.本质:量之间为加和关系,则 r为混合。
3.例:2022年,A省进出口额为2000亿元。其中,进口 1500亿元,同比增
长15%;出口 500亿元,同比增长 20%。2022 年A省进出口总额的同比增长率为:
看到问法,第一反应是考虑一般增长率,r=(2022年-2021年)/2021 年。2021
年=1500/(1+15%)+500/(1+20%),之后套公式,可以,但是计算量太大,没必
要。问进出口总额的增速,材料给进口和出口,量上存在进口+出口=进出口的关
系,问增长率,属于混合增长率。
234.例如:
(1)固定搭配:房产+地产=房地产、进口+出口=进出口、城镇+农村=全国、
博士+硕士=研究生、邮政+电信=邮电。
(2)时间累计型:上半年+下半年=全年、一季度+二季度=上半年、1~2月
+3月=一季度。
(3)逻辑型:A+非 A=全部(税收收入+非税收收入=总收入、规模以上+规
模以下=整体)。
(4)如材料中给机动车的数据、汽车的数据,问机动车中,非汽车的增长
率,汽车属于机动车的一种,总体为机动车,汽车+非汽车=机动车。
5.方法:先用口诀排除不对的选项。口诀:总体 r居中但不正中(最小 r<
总体 r<最大 r)。比如班级女同学的平均分是 99、男同学的平均分是 98,全班
同学的平均分在 98~99 之间。只有女生和男生人数相同的时候,全班平均分是
(99*10+98*10)/(10+10)=98.5,但凡人数不相等,就一定不是 98.5。资料
分析都是统计部门的真实数据,基本不会出现刚好相等的情况。
6.例 1:2020年进口额增长了 10%,出口额增长了 20%,则2020 年进出口额
可能增长了:
A.8% B.9%
C.14% D.21%
答:进口+出口=进出口,为 2 个部分,混合之后,总体增长率居中,10%<
总体r<20%,选择 C项。
7.例 2:2020年进出口额增长了 10%,出口额增长了 20%,则2020 年进口额
可能增长了:
A.8% B.12%
C.14% D.21%
答:总体增速居中,进出口为总体,总体 r10%写中间,进口和出口谁左、
谁在右不影响,根据个人习惯写即可。出口 r=20%、进出口 r=10%,总体居中,
则进口r<10%<20%,A项符合。
8.形式:部分在两边,总体在中间。
24【例 1】(2023 山东)2021 年,中国跨境电商交易规模达 14.2 万亿元,占
我国货物进出口总额的比例为 36.3%。其中出口跨境电商交易规模 11 万亿元,
同比增速 13.4%;进口跨境电商交易规模 3.2 万亿元,同比增速 14.3%。2017—
2022年第一季度,中国跨境电商领域共发生 262次投资,投资总金额 654.91亿
元。
2021 年,我国跨境电商交易规模同比增长:
A.12.8% B.13.4%
C.13.6% D.14.3%
【解析】1.问同比增长+%,问增长率,问题时间和材料时间相同,都是 2021
年。材料中给现期量,没有给基期量和增长量。出口跨境+进口跨境=跨境总体,
量存在加和关系,率为混合增长率。优先用口诀排除选项。出口 r=13.4%、进口
r=14.3%写两边,总体 r居中,排除A、B、D项,仅剩C项。【选C】
【例 2】(2022 江苏)2020 年江苏省全省网上零售额 10602亿元,比上年增
长10.0%。其中,实物商品网上零售额增长 13.9%,增速比上年快5.2 个百分点,
占社会消费品零售总额 37086亿元的比重为 24.9%,提高2.7个百分点。
能够从上述资料中推出的是:
B.2020 年江苏非实物商品网上零售额增速高于 13.9%
【解析】2.时间 2020年,问增长率,单独看题干,问“非……”的比较少,
材料中也不会给“非……”,求非 A,通常是用总体和 A 求。A+非 A=总体,问增
长率,这类题目基本就是考混合增长率。实物+非实物=总体,量之间有加和关系,
率为混合增长率。总体增长率写中间,部分增长率写两边,则非实物 r<总体 r
(10%)<实物 r(13.9%),说法错误,不选。【不选】
【注意】
1.题型:求r,给了网上零售额 r、实物商品网上零售额 r→网上零售额=实
物+非实物,量之间为加和关系,则 r为混合 r。
252.方法:总体 r居中但不正中。
三、混合增长率
题型识别:部分与总体之间的增长率关系
本质:量之间为加和关系,则 r为混合。
方法:1.口诀:①总体 r居中但不正中(最小 r<总体r<最大 r)
②总体 r偏向基期量较大的(一般可以用现期代替基期)
【3】2020 年进口额 1000 亿元,同比增长 25%,出口额 1500 亿,同比增长
20%。则 2020年进出口总额约同比增长了:
A.19% B.22%
C.24% D.26%
【注意】混合增长率:
1.题型识别:部分与总体之间的增长率关系。
2.本质:量之间为加和关系,则 r为混合。
3.方法:口诀:
(1)总体r居中但不正中(最小 r<总体 r<最大r)。
(2)总体 r 偏向基期量较大的(一般可以用现期代替基期,目前只有 2 次
反例,江苏和北京)。比如女生平均分 99 分,有 100 人;男生平均分为 98 分,
有10人,混合之后全班平均分不等于 98.5,混合之后,更接近99,因为女生人
数多于男生人数,谁的量大,起的作用更大。
4.例:2020年进口额 1000亿元,同比增长 25%,出口额1500亿,同比增长
20%。则 2020年进出口总额约同比增长了:
A.19% B.22%
C.24% D.26%
答:总体增长率在 25%和20%之间,排除 A、D项。基期量通常不给,用现期
量代替,总体增长率更接近出口额(量 1500 亿更大),平均数=(25%+20%)/2=22.5%,
则总体r在22.5%~25%之间,选择B项。
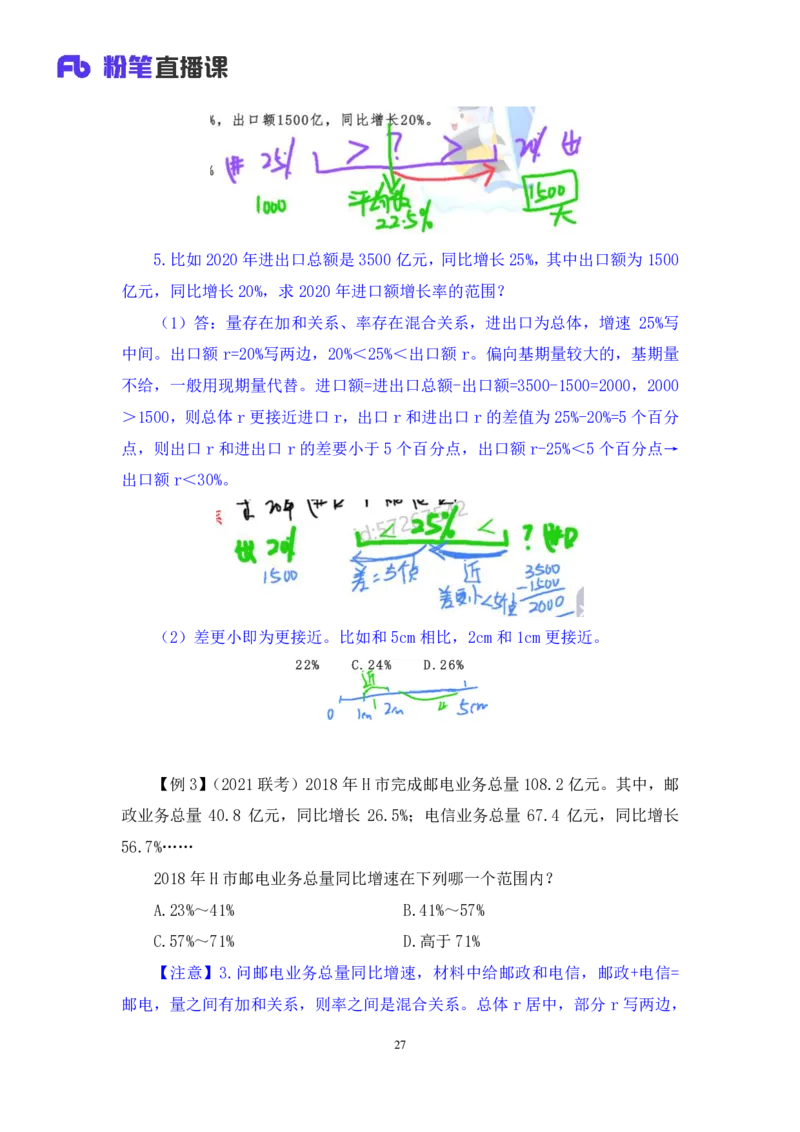
265.比如 2020年进出口总额是 3500亿元,同比增长 25%,其中出口额为 1500
亿元,同比增长20%,求2020年进口额增长率的范围?
(1)答:量存在加和关系、率存在混合关系,进出口为总体,增速 25%写
中间。出口额 r=20%写两边,20%<25%<出口额 r。偏向基期量较大的,基期量
不给,一般用现期量代替。进口额=进出口总额-出口额=3500-1500=2000,2000
>1500,则总体r 更接近进口r,出口r和进出口 r的差值为25%-20%=5 个百分
点,则出口 r 和进出口 r 的差要小于 5 个百分点,出口额 r-25%<5 个百分点→
出口额r<30%。
(2)差更小即为更接近。比如和 5cm 相比,2cm和1cm更接近。
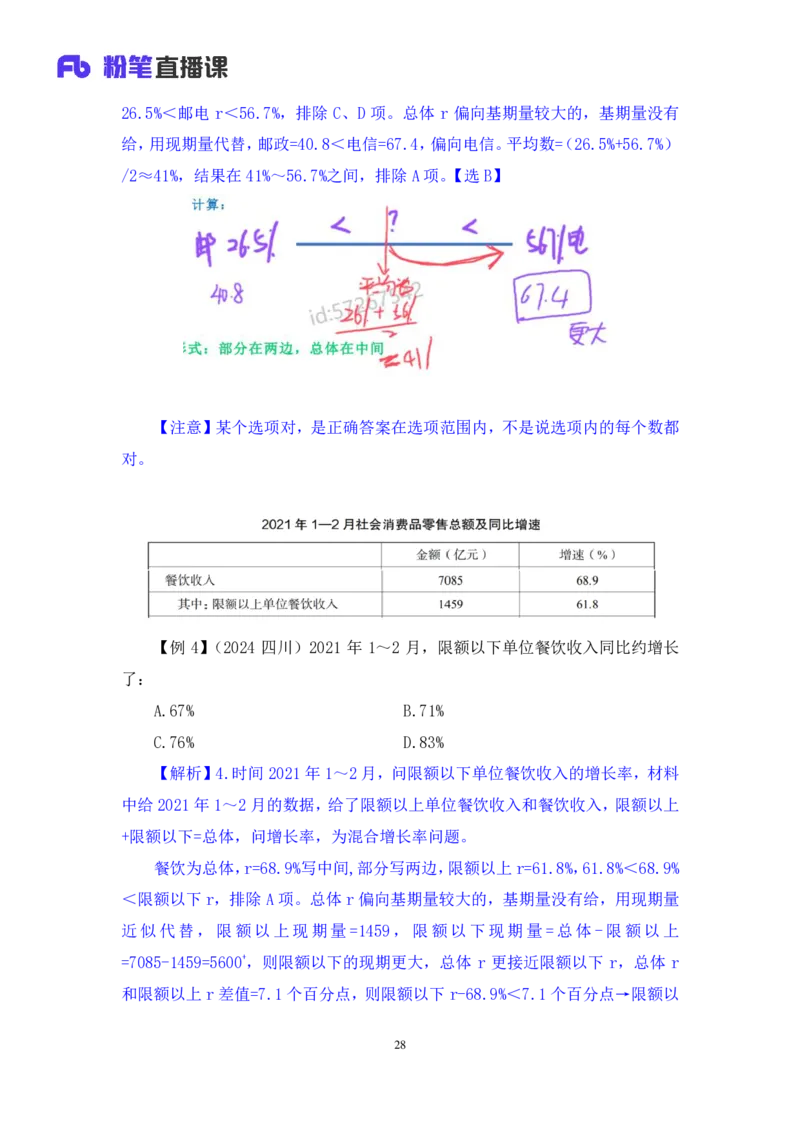
【例 3】(2021 联考)2018 年H市完成邮电业务总量 108.2亿元。其中,邮
政业务总量 40.8 亿元,同比增长 26.5%;电信业务总量 67.4 亿元,同比增长
56.7%……
2018 年H市邮电业务总量同比增速在下列哪一个范围内?
A.23%~41% B.41%~57%
C.57%~71% D.高于71%
【注意】3.问邮电业务总量同比增速,材料中给邮政和电信,邮政+电信=
邮电,量之间有加和关系,则率之间是混合关系。总体 r 居中,部分 r 写两边,
2726.5%<邮电 r<56.7%,排除 C、D 项。总体 r 偏向基期量较大的,基期量没有
给,用现期量代替,邮政=40.8<电信=67.4,偏向电信。平均数=(26.5%+56.7%)
/2≈41%,结果在41%~56.7%之间,排除A 项。【选B】
【注意】某个选项对,是正确答案在选项范围内,不是说选项内的每个数都
对。
【例 4】(2024 四川)2021 年 1~2 月,限额以下单位餐饮收入同比约增长
了:
A.67% B.71%
C.76% D.83%
【解析】4.时间 2021年1~2月,问限额以下单位餐饮收入的增长率,材料
中给2021 年1~2 月的数据,给了限额以上单位餐饮收入和餐饮收入,限额以上
+限额以下=总体,问增长率,为混合增长率问题。
餐饮为总体,r=68.9%写中间,部分写两边,限额以上 r=61.8%,61.8%<68.9%
<限额以下r,排除 A 项。总体r偏向基期量较大的,基期量没有给,用现期量
近似代替,限额以上现期量=1459,限额以下现期量=总体-限额以上
=7085-1459=5600+,则限额以下的现期更大,总体 r 更接近限额以下 r,总体 r
和限额以上r差值=7.1个百分点,则限额以下 r-68.9%<7.1个百分点→限额以
28下r<68.9%+7.1%=76%,排除C、D项,选择 B项。【选B】
【注意】
1.题型:求限额以下餐饮的 r,给了限额以上餐饮的 r、餐饮的 r→餐饮=限
额以上餐饮+限额以下餐饮,量之间为加和关系,则 r为混合r。
2.方法:口诀:
(1)总体r居中但不正中。
(2)总体r偏向基期量较大的。
线段法:增速差与基期量成反比(一般用现期近似代替基期)
基期量 *r+基期量 *r=(基期量 +基期量 )*整体 r→基期量 /基期量 =
1 1 2 2 1 2 1 2
(r-整体 r)/(整体 r-r)
2 1
【4】2020年某市总产值为 1800亿元,同比增长 6%。其中,农村产值为 40
0亿元,同比增长 13%。问:2020年该市城镇产值的同比增长率约为:
A.3.1% B.4.2%
C.5.3% D.6.4%
【注意】
1.线段法:增速差与基期量成反比(一般用现期近似代替基期)。根据方程
推导得到。通常说距离与量成反比,距离就是增速差。
292.r=增长量/基期→增长量=基期*r。以进出口为例,2020 年进出口总额增
长量=2020 年进口额增长量+2020年出口额增长量(上半年收入增长量+下半年收
入增长量=全年收入增长量),量之间是加和关系,增长量之间也是加和关系。
3.出口总额增长量=进口额增长量+出口额增长量→基期量 *r+基期量 *r=
1 1 2 2
(基期量 +基期量 )*整体 r→基期量 /基期量 =(r-整体 r)/(整体 r-r)。
1 2 1 2 2 1
得到结论:增速差与基期量成反比。增速差为挨着的 2 个增长率两两作差(大-
小)。
4.例:2020 年某市总产值为 1800 亿元,同比增长 6%。其中,农村产值为
400亿元,同比增长 13%。问:2020年该市城镇产值的同比增长率约为:
A.3.1% B.4.2%
C.5.3% D.6.4%
答:城镇+农村=该市总体,利用线段法,总体6%写中间,农村(13%)和城
镇(?)写两边,距离差分别为 13%-6%=7个百分点、6%-?。现期量之比为 400:
(1800-400)=400:1400=2:7。增速差与基期量成反比,基期量之比为 2:7,
则增速差之比为 7:2,7 份对应 7 个百分点,则 2 份对应 2 个百分点,?=6%-2
个百分点=4%,接近 B项。
【例 5】(2021 福建)2020 年,东部地区互联网业务收入 11227 亿元,同比
增长14.8%,增速较上年同期回落 9个百分点……
2020 年,互联网业务累计收入居前 5 名的广东(增长 5.2%)、北京(增长
21.5%)、上海(增长 20.9%)、浙江(增长 24.4%)和江苏(增长 8.0%)共完成
互联网业务收入10706 亿元,同比增长15.1%,增速超过全国平均水平 2.6个百
分点……
2020 年,东部地区除广东、北京、上海、浙江和江苏之外的省市互联网业
30务收入约比2019年:
A.增长 9% B.增长19%
C.减少 9% D.减少19%
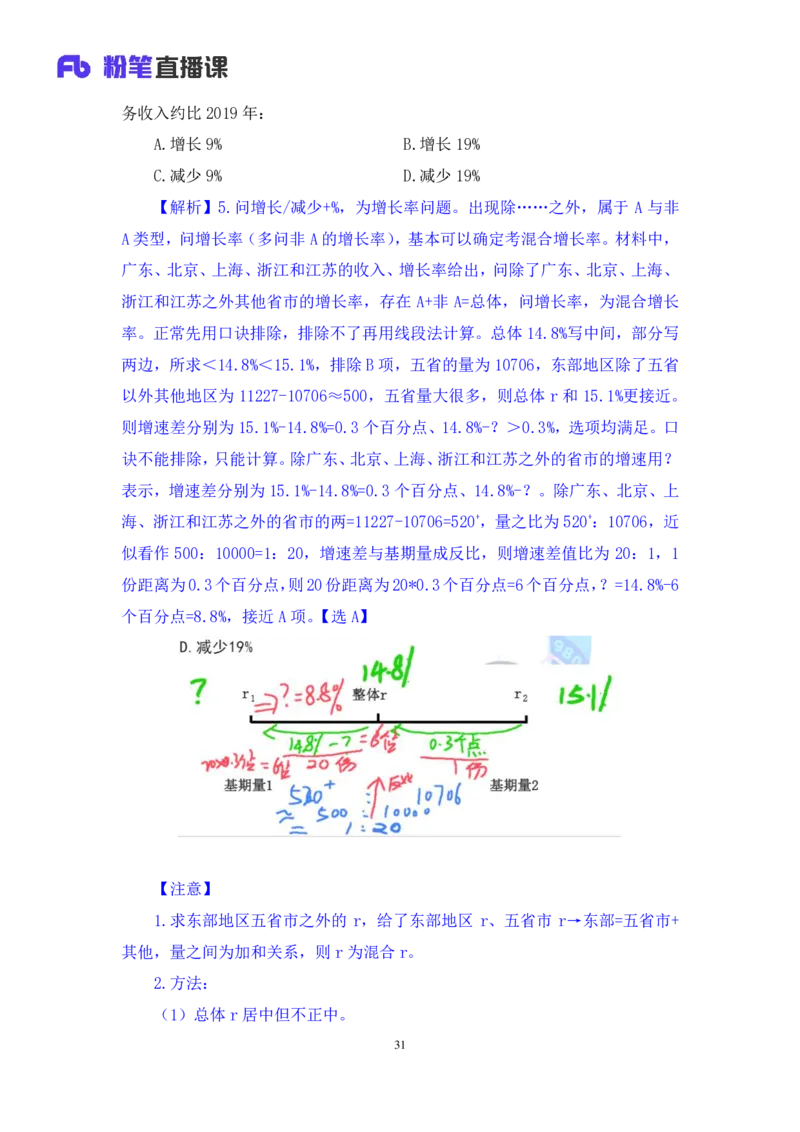
【解析】5.问增长/减少+%,为增长率问题。出现除……之外,属于 A 与非
A类型,问增长率(多问非 A的增长率),基本可以确定考混合增长率。材料中,
广东、北京、上海、浙江和江苏的收入、增长率给出,问除了广东、北京、上海、
浙江和江苏之外其他省市的增长率,存在 A+非 A=总体,问增长率,为混合增长
率。正常先用口诀排除,排除不了再用线段法计算。总体 14.8%写中间,部分写
两边,所求<14.8%<15.1%,排除B项,五省的量为10706,东部地区除了五省
以外其他地区为 11227-10706≈500,五省量大很多,则总体 r 和 15.1%更接近。
则增速差分别为15.1%-14.8%=0.3个百分点、14.8%-?>0.3%,选项均满足。口
诀不能排除,只能计算。除广东、北京、上海、浙江和江苏之外的省市的增速用?
表示,增速差分别为 15.1%-14.8%=0.3个百分点、14.8%-?。除广东、北京、上
海、浙江和江苏之外的省市的两=11227-10706=520+,量之比为 520+:10706,近
似看作 500:10000=1:20,增速差与基期量成反比,则增速差值比为 20:1,1
份距离为0.3个百分点,则20份距离为20*0.3个百分点=6个百分点,?=14.8%-6
个百分点=8.8%,接近 A项。【选A】
【注意】
1.求东部地区五省市之外的 r,给了东部地区 r、五省市 r→东部=五省市+
其他,量之间为加和关系,则 r为混合r。
2.方法:
(1)总体r居中但不正中。
31(2)总体r偏向基期量较大的。
(3)线段法:增速差与基期量成反比。
【注意】
1.间隔增长率:间隔一年问增长率。公式:r =r+r+r*r。
间 1 2 1 2
2.年均增长率:问年均增长率是多少、年均增长率最快的是谁,公式:(1+r)
n=现期量/基期量,n=年份差,比较大小直接比较现期量/基期量,计算用代入。
3.混合增长率:研究部分增长率与总体增长率之间的关系,量之间是加和关
系,率之间是混合关系。能排除先排除,不能排除只能线段法计算。线段法:距
离和量成反比,距离为挨着的 r两两作差,大-小=正数,如果是负数,错的几率
更高,基期量一般不会给,用现期量代替。
第九节 广东特色直接找数
考查点:查找信息的准度与速度
难度:极简单
【注意】2024 年省考大纲出现很多新的例题:
1.考查点:查找信息的准度与速度,只考找信息的速度。
2.难度:极简单。
3.2024 年考了一篇,其中 2个是稍微带一点计算的、3个纯找信息就能得到
答案的。
32【例 1】(2024 广东)为推动广东技工与广东制造共同成长,近年来,广东
紧紧围绕壮大 20 个战略性产业集群,紧密对接产业升级和技术变革趋势,开展
新产业工人职业技能提升工程,培育掌握新技术的产业新工匠。广东充分发挥经
济大省、制造业大省的优势,将产教融合、校企合作融入技能人才培养全过程,
打造了全国最大的技工教育体系。
2023年,广东共有技工院校148所,实现21个地级以上市技师学院全覆盖;
在校生 65 万人,占全国的七分之一;面向先进制造业、战略性新兴产业、现代
服务业建设 233 个省级重点专业和 50 个特色专业;与 100 多家世界 500 强企业
及国内800多家大型企业开展深度合作,实现教学与企业岗位无缝对接,精准培
养产业急需人才。技工院校招生人数、教研成果、技能竞赛、就业率等九项主要
指标均居全国第一。
关于广东技能人才培养,以下表述不准确的是:
A.注重产教融合、校企合作
B.实现教学与企业岗位无缝对接
C.精准培养产业急需人才
D.强调提升全体学生技能竞赛成绩
【解析】1.问不准确的。先浏览选项,带着选项找材料。
A项:“将产教融合、校企合作融入技能人才培养全过程”,说法正确,不选。
B项:“实现教学与企业岗位无缝对接”,正确,不选。
C项:“精准培养产业急需人才”,正确,不选。
D 项:“技工院校招生人数、教研成果、技能竞赛、就业率等九项主要指标
均居全国第一”,没有说强调,且不是全体成绩,错误,当选。【选 D】
【注意】如果胆子大,可以不看材料,直接读选项,A、B、C项都是很好的
事情,D 项与现在强调的给小学生减负矛盾,根据常识猜 D 项。如果没时间找,
可以这么猜,但找是 100%正确的,猜有风险。
【例 2】(2015 广东)2014年,全国汽车产销分别是 2372万辆和 2349万辆,
33同比增长7.3%和6.9%。汽车销售排名前十位的企业集团销售合计为2107.7万辆,
比上年同期增长8.9%,高于全行业增速2个百分点。
受宏观经济和相关政策法规影响,今年的商用车市场销量降幅较大。全年商
用车销售完成 379 万辆,同比下降 6.5%,分车型看,其中货车销售 318 万辆,
同比下降8.9%,客车销售 61万辆,同比增长 8.4%。货车车型中,受国四排放标
准执行后带来成本上升和厂家生产准备不足等原因影响,使轻型货车出现了大幅
下降,全年降幅达到了 12.9%。由于轻型货车占到货车的比重较高,导致货车整
体出现了较高降幅。客车方面受到城市公交(含新能源车)、校车增长及轻型客
车带动,使客车市场继续保持平稳增长。
2014 年商用车市场销量降幅较大,原因在于:
A.受政府全面出台支持发展新能源汽车政策影响
B.受宏观经济和相关政策法规影响
C.受外国品牌汽车价格下降影响
D.受中国品牌乘用车销售占有率下降影响
【注意】2.问原因在于。根据“受宏观经济和相关政策法规影响,今年的商
用车市场销量降幅较大”,直接选B项。【选 B】
【注意】重点是耐心,认真找。
【例 3】(2014 吉林)中国社科院世界社保研究中心发布《中国养老基金发
展报告2012》。报告显示,2010年有15个省份收不抵支,缺口达 679 亿元;2011
年收不抵支的省份虽然减少到 14个,但收支缺口高于 2010年,2011 年达766.5
亿元。
报告分析显示,我国养老金地区差异较大。到 2011 年,我国有辽宁、黑龙
江、天津、上海等 14个省份养老金收不抵支。但是,在面临亏损的同时,18个
省份养老金收入则远远大于支出。其中,广东结余最多,达到 519 亿元;浙江、
江苏、北京等省份结余也在二三百亿元。
从 10 年来的数据看,2002 年,全国 29 个省份养老金收不抵支,随着时间
推移,越来越多的省份走出了这一困境,到 2011年则为14个,数量上呈逐年减
34少的趋势。不过值得注意的是,在出现收不抵支的省份中,其负结余规模不断扩
大,亏损额由2002 年的407.6亿元达到2011 年的766.5亿元。而且在向少数省
份集中,尤其是黑龙江、辽宁等老工业地区。
对比 2010 年和 2011 年排名前 10 的亏损省份显示,上海、黑龙江、广西的
排名变化比较明显。其中,上海结余由 2010 年的 139.5 亿元减少到 2011 年的
25 亿元,排名从第 2 位下移到 10 位之外。主要原因是,上海市 2011 年将外来
务工人员和城郊就业人员纳入养老保险制度,使得当年养老基金大幅增收。
下列说法正确的是:
A.报告分析显示,我国养老金不存在地区差异
B.对比 2010 年和 2011 年排名前 10 的亏损省份显示,吉林的排名变化比较
明显
C.报告分析显示,到 2011年,我国养老金收入远大于支出的省份有 14个
D.养老金出现收不抵支的省份中,其负结余规模不断扩大
【注意】3.问正确的是。
第一段说“2010 年有15个省份收不抵支”,是养老金的情况;第二段说“报
告分析显示,我国养老金地区差异较大”,说地区差异。第三段“从 10年来的数
据看”;第四段“对比 2010年和2011年排名前 10的亏损省份显示”大概画一下
每段第一句话,找数速度能较快。
综合分析,从 C项入手。
C项:第二段说地区相关,“到2011年,我国有辽宁、黑龙江、天津、上海
等14个省份养老金收不抵支”,收不抵支和选项不是同一件事。“18 个省份养老
金收入则远远大于支出”,是18个,错误,排除。
D项:付结余不用理解,找信息即可。第二段没有出现有效信息。第一段给
出“2010 年有15个省份收不抵支,缺口达 679亿元;2011年收不抵支的省份虽
然减少到14个,但收支缺口高于 2010年,2011 年达766.5亿元”,收支缺口 2011
年高于 2010 年;第三段给出“不过值得注意的是,在出现收不抵支的省份中,
其负结余规模不断扩大”,说明是多个年份。为第三段原句,正确,当选。
A项:第二段说“报告分析显示,我国养老金地区差异较大”,错误,排除。
B项:第四段说“对比2010年和2011年排名前 10的亏损省份显示,上海、
35黑龙江、广西的排名变化比较明显”,没有吉林,错误,排除。【选 D】
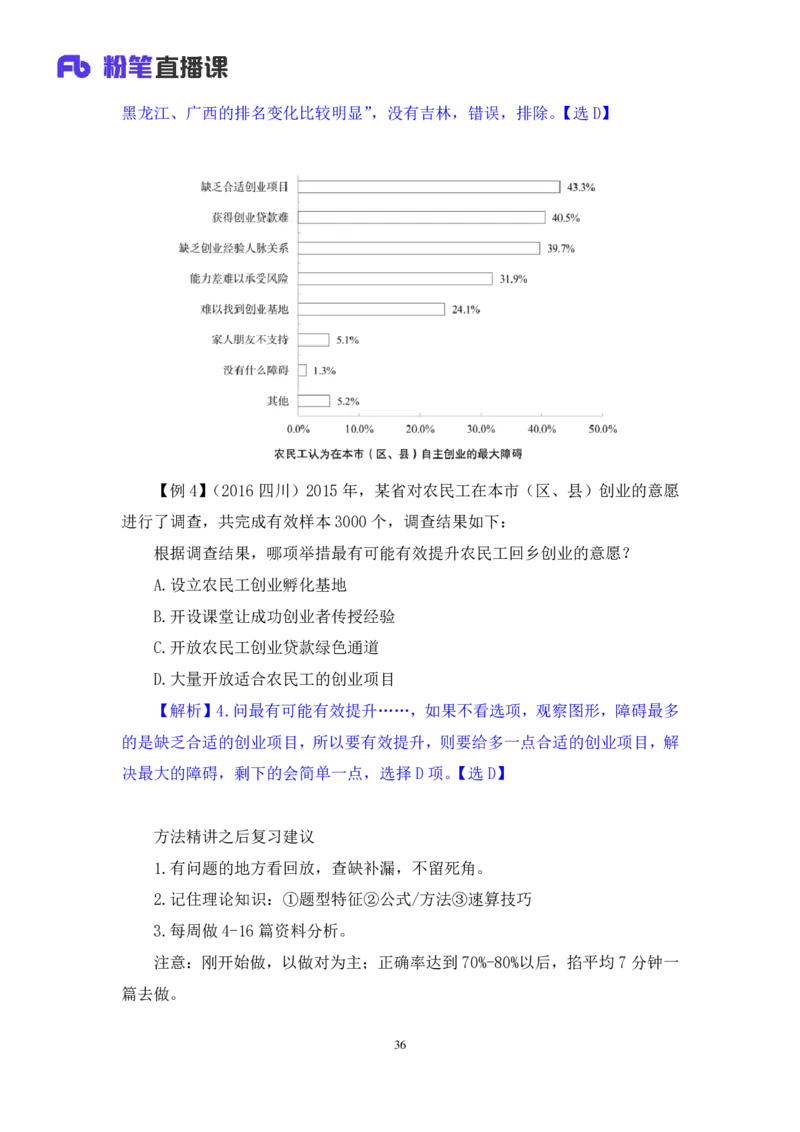
【例 4】(2016 四川)2015年,某省对农民工在本市(区、县)创业的意愿
进行了调查,共完成有效样本 3000个,调查结果如下:
根据调查结果,哪项举措最有可能有效提升农民工回乡创业的意愿?
A.设立农民工创业孵化基地
B.开设课堂让成功创业者传授经验
C.开放农民工创业贷款绿色通道
D.大量开放适合农民工的创业项目
【解析】4.问最有可能有效提升……,如果不看选项,观察图形,障碍最多
的是缺乏合适的创业项目,所以要有效提升,则要给多一点合适的创业项目,解
决最大的障碍,剩下的会简单一点,选择 D 项。【选D】
方法精讲之后复习建议
1.有问题的地方看回放,查缺补漏,不留死角。
2.记住理论知识:①题型特征②公式/方法③速算技巧
3.每周做 4-16 篇资料分析。
注意:刚开始做,以做对为主;正确率达到 70%-80%以后,掐平均 7 分钟一
篇去做。
36【注意】方法精讲之后复习建议:
1.有问题的地方看回放,查缺补漏,不留死角。
2.记住理论知识:
(1)题型特征。
(2)公式/方法。
(3)速算技巧。
3.每周做 4~16 篇资料分析。开始不要在意时间,以正确率为主。
4.注意:刚开始做,以做对为主;正确率达到 70%~80%以后,掐平均 7 分
钟一篇去做。
37【答案汇总】
倍数 1-5:DCBBD
间隔增长率 1-3:CDC
年均增长率 1-3:BDC
混合增长率 1-5:C不选BBA
广东特色直接找数 1-4:DBDD
38遇见不一样的自己
Be your better self
39