试题答案-安徽A10联盟2024-2025学年高二上学期9月初开学摸底考数学（B卷）(1)_1多考区联考_09142024-2025学年高二上学期9月初开学数学试卷1

A10 联盟 2023 级高二上学期 9 月初开学摸底考 数学（北师大版）试题 命题单位：淮南二中数学教研组 编审单位： 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.满分 150分，考试时间 120分钟.请 在答题卡上作答. 第Ⅰ卷（选择题 共 58分） 一、选择题：本大题共 8个小题，每小题 5分，共 40分．在每小题所给四个选项中，只有一 项是符合题意的． A={−3,−2,0,1,2} B= { x∈N x2 −x−6≥0 } A(  B )= 1. 已知集合 ， ，则 N （ ） A. {−3,−2,0,1,2 } B. {−1,0,1,2 } C. { 0,1,2 } D. { 1,2 } 【答案】C 【解析】 【分析】根据一元二次不等式化简集合B= { x∈N x≥3或x≤−2 } ，即可利用集合的补集以及交集定义求 解. 【详解】由B= { x∈N x2 −x−6≥0 } 可得B= { x∈N x≥3或x≤−2 } ， 故 B= { x∈N −2< x<3 } ={ 0,1,2 } ， N 故A∩ (  B ) ={ 0,1,2 } ， N 故选：C. 1 1 2. 设a,b∈R，则“ >b>0”是“a< ”的（ ） a b A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 【答案】A 【解析】 【分析】利用不等式的性质化简，即可根据逻辑关系求解. 1 【详解】由 >b>0可得a >0,b>0,ab<1， a 第1页/共22页 学科网（北京）股份有限公司1 ab−1 ab<1 ab>1 由a< 可得 <0⇒ 或 ， b b b>0 b<0 1 1 1 1 故 >b>0能得到a< ，同时a< 也无法推出 >b>0， a b b a 1 1 故“ >b>0”是“a< ”的充分不必要条件， a b 故选：A. 3. 已知某学校参加学科节数学竞赛决赛的8人的成绩（单位：分）为：72，78，80，81，83，86，88， 90，则这组数据的第75百分位数是（ ） A. 86 B. 87 C. 88 D. 90 【答案】B 【解析】 【分析】根据样本数据百分位数的定义求解即可. 【详解】将数据从小到大排序得72,78,80,81,83,86,88,90， 因为8×75%=6， 86+88 所以第75百分位数是 =87． 2 故选：B． 4. 一个质地均匀的正四面体木块的四个面上分别标有数字1，2，3，4.连续抛掷这个正四面体木块两次， 并记录每次正四面体木块朝下的面上的数字，记事件A为“第一次向下的数字为2或3”，事件B为“两次向 下的数字之和为奇数”，则下列结论正确的是（ ） 1 A. P(A)= B. 事件A与事件B互斥 4 1 C. 事件A与事件B相互独立 D. P(A∪B)= 2 【答案】C 【解析】 【分析】利用互斥事件、相互独立事件的意义及古典概率公式逐项计算判断作答. 【详解】依题意，抛掷正四面体木块，第一次向下的数字有1，2，3，4四个基本事件，则 2 1 P(A)= = ，A不正确； 4 2 第2页/共22页 学科网（北京）股份有限公司事件B含有的基本事件有8个：(1,2),(1,4),(2,1),(2,3),(3,2),(3,4),(4,1),(4,3)， 其中事件(2,1),(2,3),(3,2),(3,4)发生时，事件A也发生，即事件A，B可以同时发生，B不正确； 8 1 4 1 抛掷正四面体木块两次的所有基本事件有16个，P(B)= = ,P(AB)= = = P(A)P(B)， 16 2 16 4 即事件A与事件B相互独立，C正确； 1 1 1 3 P(A∪B)= P(A)+P(B)−P(AB)= + − = ，D不正确. 2 2 4 4 故选：C 4  π π  π  5. 已知tan2θ= ，θ∈ 0, ，若cos −θ  =mcos +θ ，则实数m的值为（ ） 3  4 4  4  A. −3 B. −2 C. 3 D. 2 【答案】C 【解析】 m−1  π 1 【分析】根据余弦和差公式化简得到tanθ= ，由正切二倍角公式和θ∈ 0, 得到tanθ= ，从而得 m+1  4 2 到方程，求出实数m的值. π π  π π  【详解】cos cosθ+sin sinθ=mcos cosθ−sin sinθ ， 4 4  4 4  2 2  2 2  即 cosθ+ sinθ=m cosθ− sinθ，   2 2  2 2  cosθ+sinθ=m ( cosθ−sinθ) ，故 ( 1+m ) sinθ=( m−1 ) cosθ， m−1 则tanθ= ， m+1 2tanθ 4 由于tan2θ= = ，故2tan2θ+3tanθ−2=0， 1−tan2θ 3 1 解得tanθ=−2或 ， 2  π 1 因为θ∈ 0, ，所以tanθ>0，故tanθ= ，  4 2 m−1 1 即 = ，解得m=3. m+1 2 故选：C 第3页/共22页 学科网（北京）股份有限公司         6. 已知平面向量e 和e 满足 e =2 e =2，e 在e 上的投影向量为−e ，则e 在e 上的投影向量为 1 2 2 1 2 1 1 1 2 （ ）  1 1 A. − e B. − 4 2 2   1 C. − e D. −e 2 2 2 【答案】A 【解析】        e ⋅e e 【分析】根据e 在e 上的投影向量得到方程，求出e ⋅e =−1，进而利用 12 ⋅ 2 求出答案. 2 1 1 2 e e 2 2     【详解】因为 e =2 e =2，所以 e =2, e =1， 2 1 2 1         e ⋅e e  e ⋅e e 2 在e 1 上的投影向量为−e 1 ，故 1 e  2 ⋅ e 1 =−e 1 ，故 1 e  2 2 =−1 ， 1 1 1   所以e ⋅e =−1， 1 2      e ⋅e e 1  则e 在e 上的投影向量为 12 ⋅ 2 =− e . 1 2 e e 4 2 2 2 故选：A lgx ,0< x≤10  7. 已知函数 f ( x )= 1 ，若a，b，c，d互不相等，且 f ( a )= f ( b )= f ( c )= f ( d ) ，则 − x+6 ,x>10   2 a+b+c+d 的取值范围为（ ） A. [ 26,+∞) B. ( 14,+∞)  341  221 C. 26,  D. 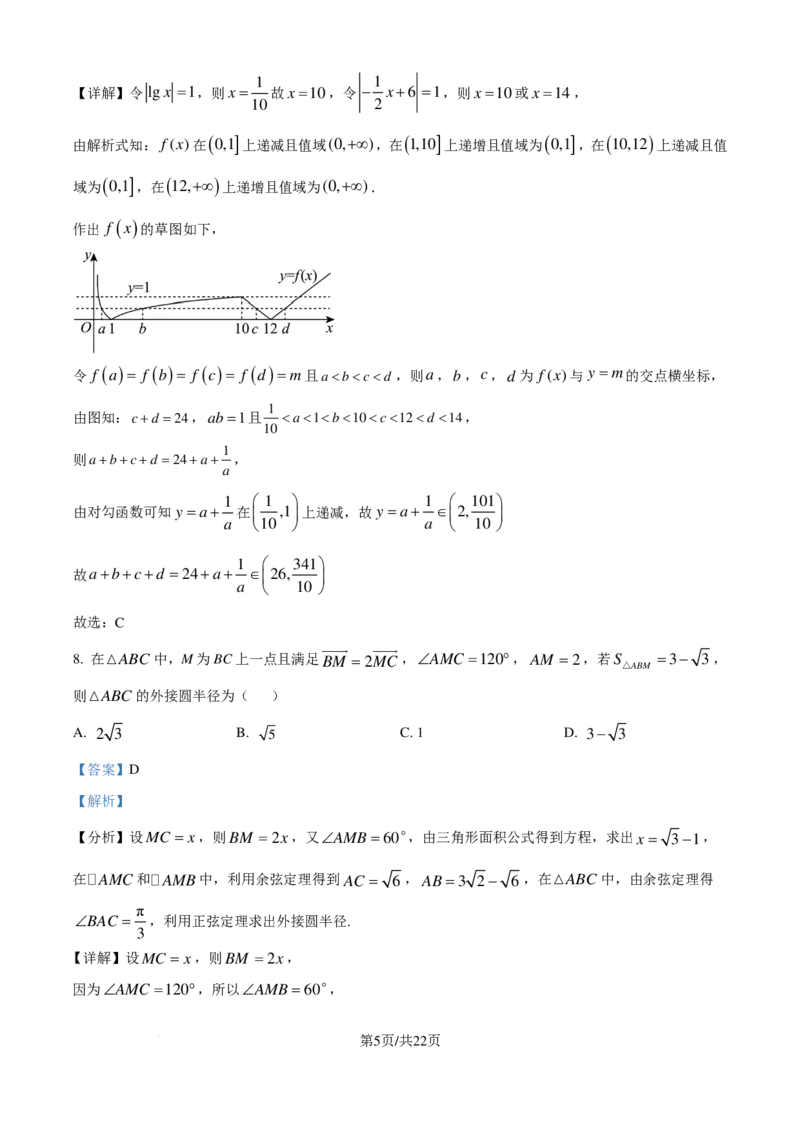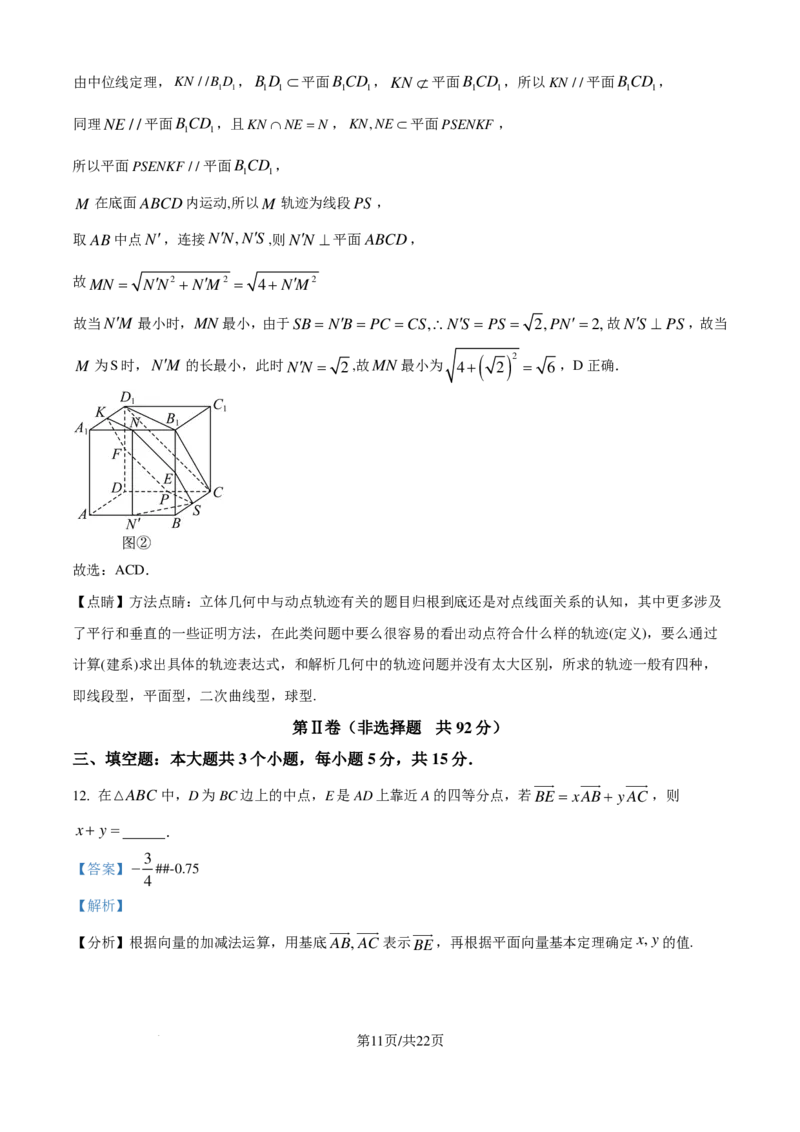26,   10   10  【答案】C 【解析】 【分析】由分段函数的性质画出函数图象，若 f ( a )= f ( b )= f ( c )= f ( d )=m a0.6， 所以第60百分位数位于第三个区间内， 0.6−0.5 所以第60百分位数为80+ ×10=82.5分. 0.9−0.5 【小问2详解】 把6月1日—6月7日的样本记为x ,x ,x ?··,x ，其平均数记为x ，方差记为s2， 1 2 3 40000 x 把6月8日—6月14日的样本记为y ,y ,y ?··,y ，其平均数记为y，方差记为s2，总样本方差为 1 2 3 60000 y s2， 40000 40000 则总样本平均数z = ×85+ ×95=91， 60000+40000 60000+40000 { } 由方差的定义，样本总方差为：s2 = 1 4  s2 +( x −z )2+6  s2 + ( y−z )2 10  x   y  第14页/共22页 学科网（北京）股份有限公司1 所以s2 = ×  4×( 74+36 )+6×( 69+16 )  =95， 10 所以总样本的平均数为91，方差为95. 16. 已知锐角ABC的三个角A，B，C的对边分别为a，b，c，且acosC+ 3asinC−b−c=0． （1）求A； （2）若a=2，求ABC周长的取值范围． π 【答案】（1）A= 3 ( （2） 2+2 3,6  【解析】 【分析】（1）利用正弦定理以及三角恒等变换等知识求得正确答案. （2）将b,c转化为B来表示，再根据三角函数的性质求得正确答案. 【小问1详解】 由正弦定理得sinAcosC+ 3sinAsinC−sinB−sinC =0， 则sinAcosC+ 3sinAsinC−sin ( A+C )−sinC =0， 所以sinAcosC+ 3sinAsinC−sinAcosC−cosAsinC−sinC =0， 即 3sinAsinC−cosAsinC−sinC =0， π 由于00，所以 3sinA−cosA=1， 2  π  π 1 π π π π 则2sinA−  =1，sinA−  = ，由于0< A< ,− < A− < ，  6  6 2 2 6 6 3 π π π 所以A− = ,A= . 6 6 3 【小问2详解】 2 b c 4 = = = 若a=2，由正弦定理得 π sinB sinC 3 ， sin 3 4 4 所以b= sinB,c= sinC ， 3 3 4 4 所以三角形ABC 的周长为a+b+c=2+ sinB+ sinC 3 3 第15页/共22页 学科网（北京）股份有限公司4 4 π  =2+ sinB+ sin +B 3 3 3  4 4  3 1  =2+ sinB+  cosB+ sinB   3 3 2 2  1 3   π =2+4  cosB+ sinB  =2+4sinB+ ， 2 2   6  π 0< B<   2 π π 由于三角形ABC是锐角三角形，所以 ，所以 < B< ，  π π 6 2 +B> 3 2 π π 2π 3  π  π 所以 < B+ < ，所以 时，H ( m ) = H −  = ×  −  +t⋅  −  +1=− t+ =− ， 2 2 min  2 2  2  2 2 8 8 解得t =2， 3 3 3 3 1 1 7 当− ≤−t ≤ ，即− ≤t ≤ 时，H ( m ) = H (−t )= (−t )2 +t×(−t )+1=− t2 +1=− ， 2 2 2 2 min 2 2 8 15 3 3 解得t =± ，又− ≤t ≤ ，因此不符合题意， 2 2 2 3 3 3 1 3 2 3 3 17 7 当−t > ，即t <− 时，H ( m ) = H  = ×   +t× +1= t+ =− ， 2 2 min 2 2 2 2 2 8 8 解得t =−2， 综上知，t=±2 【点睛】方法点睛： 1.函数最值与值域的求法：单调性法；不等式法；配方法；换元法；数形结合法；分离常数法；导数法. 2.闭区间上二次函数最值问题的解法：抓住“三点一轴”数形结合，三点是指区间两个端点和中点，一轴是 指对称轴，结合图象，根据函数的单调性及分类讨论的思想求解. 19. 对于集合A={θ,θ,,θ} 和常数θ，定义： 1 2 n 0 sin2(θ−θ)+sin2(θ −θ)++sin2(θ −θ) σ= 1 0 2 0 n 0 为集合A相对的θ的“正弦标准差”． 0 n 第19页/共22页 学科网（北京）股份有限公司π π π （1）若集合A= , ，θ = ，求A相对的θ的“正弦标准差”； 6 3 0 4 0 π  3π  3π 7π （2）若集合A= 4 ,α,β  ，是否存在α∈   4 ,π  ，β∈   2 , 4   ，使得相对任何常数θ 0 的“正弦标 准差”是一个与θ无关的定值？若存在，求出α，β的值；若不存在，请说明理由． 0 6− 2 【答案】（1） 4 11π 19π （2）存在α= ，β= ，使得相对任何常数θ的“正弦标准差”是一个与θ无关的定值，理由见解 0 0 12 12 析 【解析】 【分析】（1）根据题意，代入公式计算，结合正弦差角公式得到答案； sin2α+sin2β=−1 1 （2）利用三角恒等变换化简，从而 ，平方相加，得到cos ( 2α−2β)=− ，结合 cos2α+cos2β=0 2 3π  3π 7π 4π α∈  ,π ， β∈  ,  求出 2α−2β=− ，从而消元，结合 cos2α+cos2β=0 得到  4   2 4  3 3 11π 11π 19π tan2α=− ，得到2α= ，求出α= ，β= . 3 6 12 12 【小问1详解】 π π π π  π  π π π sin2  −  +sin2  −  sin2  −  +sin2 sin2 +sin2 6 4 3 4  12 12 12 12 π ， σ= = = =sin 2 2 2 12 π π π π π π π 3 2 1 2 6− 2 其中sin =sin −  =sin cos −cos sin = × − × = . 12 3 4 3 4 3 4 2 2 2 2 4 【小问2详解】 11π 19π 存在α= ，β= ，使得相对任何常数θ的“正弦标准差”是一个与θ无关的定值，理由如下： 0 0 12 12 π  sin2  −θ  +sin2(α−θ)+sin2(β−θ) 4 0  0 0 π  1−cos 2 −2θ 0   1−cos ( 2α−2θ) 1−cos ( 2β−2θ) = + 0 + 0 2 2 2 第20页/共22页 学科网（北京）股份有限公司3 1 = − ( sin2θ +cos2αcos2θ +sin2αsin2θ +cos2βcos2θ +sin2βsin2θ) 2 2 0 0 0 0 0 3 1 = −   sin2θ ( 1+sin2α+sin2β)+cos2θ ( cos2α+sin2β)  ， 2 2 0 0 sin2α+sin2β=−1 只需 ，则( cos2α+cos2β)2 +( sin2α+sin2β)2 =1， cos2α+cos2β=0 1 即2+2cos2αcos2β+2sin2αsin2β=1，整理得cos ( 2α−2β)=− ， 2 3π  3π 7π 因为α∈  ,π，β∈  , ，  4   2 4  3π   7π  7π  所以2α∈  ,2π，2β∈  3π, ，−2β∈  − ,−3π  ，  2   2   2  则2α−2β∈(−2π,π ) ， 4π 4π 所以2α−2β=− ，则2β=2α+ ， 3 3  4π 所以cos2α+cos2β=cos2α+cos2α+  =0，  3  4π 4π 即cos2α+cos2αcos −sin2αsin =0， 3 3 3 整理得cos2α+ 3sin2α=0，故tan2α=− ， 3 3π  11π 11π 因为 2α∈  ,2π，所以2α= ，α= ，  2  6 12 4π 11π 4π 19π 19π 则2β=2α+ = + = ，β= ， 3 6 3 6 12 11π 19π sin2α+sin2β=−1 检验，将α= ，β= 代入 得 12 12 cos2α+cos2β=0  11π 19π  π 7π 1  1 sin +sin =sin −  +sin =− +  −  =−1  6 6  6 6 2  2  ，满足要求，  11π 19π  π 7π π π cos +cos =cos −  +cos =cos −cos =0   6 6  6 6 6 6 11π 19π 故存在α= ，β= ，使得相对任何常数θ的“正弦标准差”是一个与θ无关的定值， 0 0 12 12 π  sin2  −θ  +sin2(α−θ)+sin2(β−θ) 此时 4 0  0 0 2 . σ= = 3 2 第21页/共22页 学科网（北京）股份有限公司【点睛】方法点睛：新定义问题的方法和技巧， （1）可通过举例子的方式，将抽象的定义转化为具体的简单的应用，从而加深对信息的理解； （2）可用自己的语言转述新信息所表达的内容，如果能清晰描述，那么说明对此信息理解的较为透彻； （3）发现新信息与所学知识的联系，并从描述中体会信息的本质特征与规律； （4）如果新信息是课本知识的推广，则要关注此信息与课本中概念的不同之处，以及什么情况下可以使用 书上的概念. 第22页/共22页 学科网（北京）股份有限公司