文档内容
2023~2024 学年度第一学期四校联考(二)
数学试卷
命题学校:东莞市第六高级中学 命题:周国真 审题:王蔷薇
说明:本试卷共4页,22道题,满分150分。考试用时120分钟。
注意事项:1. 答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座
位号填写在答题卡上。用2B铅笔将试卷类型(A)填涂在答题卡相应位置上。
2. 选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑。如需改动,
用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上。
3. 非选择题的作答:用签字笔直接写在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题
卡上的非答题区域均无效。
一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合
题目要求的.
1. 已知全集 ,集合 , ,则图中的阴影部分表示的集合
为
A. B.
C. D.
2.在等差数列 中,若 , ,则 ( )
A. 16 B. 18 C. 20 D. 22
3.已知 ,则 的值为( )
A. B. C. D.
试卷第1页,共3页
学科网(北京)股份有限公司4.设 为正项等差数列 的前 项和.若 ,则 的最小值为( )
A. B. C. D.
5.命题“∀1≤x≤2,x2-a≤0”为真命题的一个充分不必要条件是( )
A.a≥4 B.a≥5 C.a≤4 D.a≤5
6. 已知函数 满足 其中 是 的导数 ,若 , ,
,则下列选项中正确的是( )
A. B. C. D.
7. 若函数 恰有两个零点,则实数k的取值范围为( )
A. B. C. D.
8. 若直角坐标平面内A,B两点满足:①点A,B都在函数 的图象上;②点A,B关于原点对
称,则称点 是函数 的一个“姊妹点对”,点对 与 可看作是同一个“姊妹
点对”.已知函数 恰有两个“姊妹点对”,则实数a的取值范围是( )
A. B. C. D.
二、多选题:本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,有多项符合题目
要求.全部选对得 5 分,部分选对的得 2 分,有选错的得 0 分.
9. 下列命题为真命题的是( )
试卷第2页,共3页
学科网(北京)股份有限公司A. 若 ,则 B. 若 ,则
C. 若关于 的不等式 的解集为 ,则
D. 函数 在区间 内单调递增,则实数m的取值范围为
10. 在数列 中, ,且对任意不小于2的正整数n, … 恒成立,
则 下列结论正确的是( )
A. B. C. , , 成等比数列 D. …
11. 下列四个命题中,错误的是( )
A. “ ”是“关于x的方程 有两个实数解”的必要不充分条件
B. 命题“ R,使得 ”的否定是:“对 R,均有 ”
C. 若 ,则函数 的最小值是2
D. 若函数 在 有极值0,则 , 或 ,
12. 已知 , 分别是函数 和 的零点,则( )
试卷第3页,共3页
学科网(北京)股份有限公司A. B. C. D.
三、填空题:本题共 4 小题,每小题 5 分,共 20 分.
13.数列 中, , , 若其前k项和为126,则 __________.
14.已知函数 定义域为R,满足 ,当 时 ,则
______.
15.已知定义在R上的函数 满足:对任意x, 都有 ,且当 时,
, 对任意 恒成立,则实数k的取值范围是 .
16. 函数 在 上不单调,则实数a的取值范围是 .
四、解答题:本题共 6 小题,共 70 分.解答应写出必要的文字说明,证明过程或演算步骤.
17. 本小题10分
已知曲线 在点 处的切线的斜率为3,且当 时,函数
取得极值.
(1)求函数在点 处的切线方程; (2)求函数的极值;
(3)若存在 ,使得不等式 成立,求m的取值范围.
试卷第4页,共3页
学科网(北京)股份有限公司18. 本小题12分
已知角θ 的终边上一点 ,且 ,
(1)求tan θ的值; (2)求 的值.
(3)若 , ,且 ,求 的值.
19. 本小题12分
已知数列 的前n项和为 ,且 ,数列 的前n项积为 ,且
求 , 的通项公式; 求数列 的前n项和
20. 本小题12分
已知函数 为自然对数的底数
求函数 的单调区间;
求函数 在区间 上的最大值和最小值.
试卷第5页,共3页
学科网(北京)股份有限公司21. 本小题12分
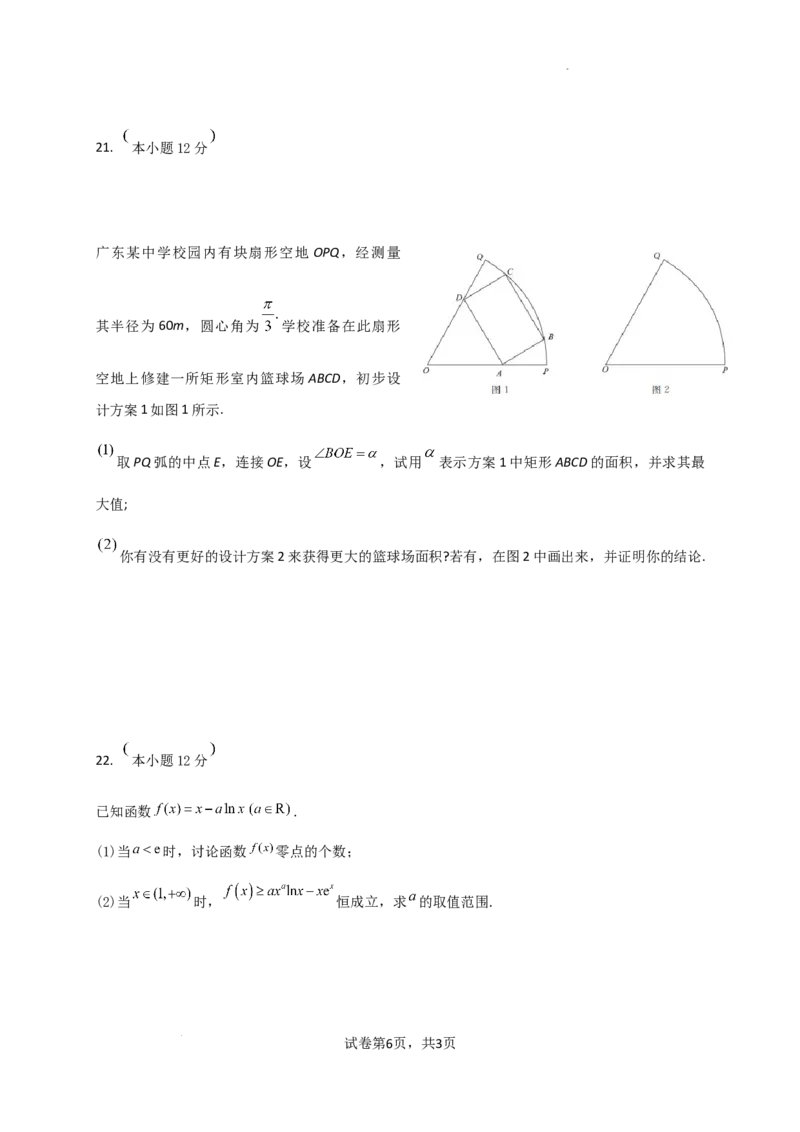
广东某中学校园内有块扇形空地 OPQ,经测量
其半径为60m,圆心角为 学校准备在此扇形
空地上修建一所矩形室内篮球场 ABCD,初步设
计方案1如图1所示.
取PQ弧的中点E,连接OE,设 ,试用 表示方案1中矩形ABCD的面积,并求其最
大值;
你有没有更好的设计方案2来获得更大的篮球场面积?若有,在图2中画出来,并证明你的结论.
22. 本小题12分
已知函数 .
(1)当 时,讨论函数 零点的个数;
(2)当 时, 恒成立,求 的取值范围.
试卷第6页,共3页
学科网(北京)股份有限公司