文档内容
定远育才学校 2025-2026 学年高三(上)1 月考试卷
数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若 ,则 ( )
z(1+i)=i2025 z=
1 1 1 1 1 1 1 1
A. + i B. - + i C. - i D. - - i
2 2 2 2 2 2 2 2
2.已知命题p:∃x∈R,ax2+2x+3≤0为假命题,则实数a的取值范围是( )
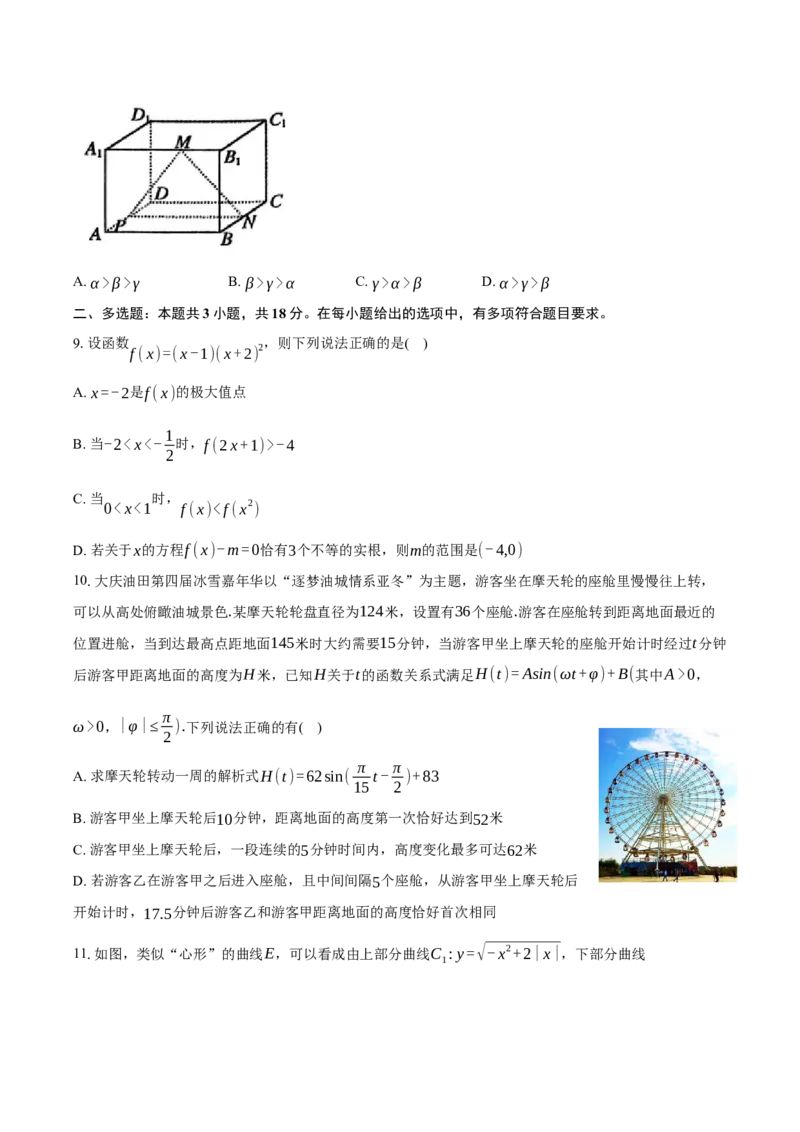
A. { | 1} B. { | 1}. C. { | 1} D. { | 1}
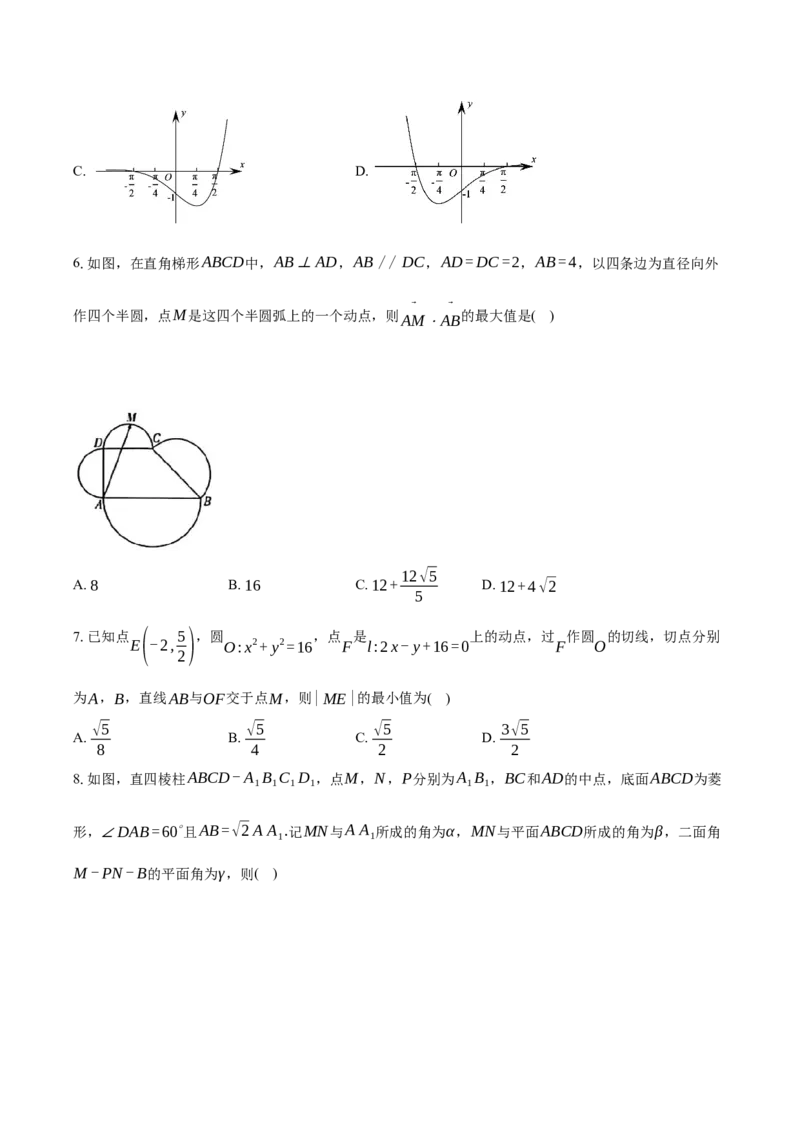
a 0 a a≥ a 0β>γ B. β>γ>α C. γ>α>β D. α>γ>β
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.设函数 ,则下列说法正确的是( )
f(x)=(x-1)(x+2) 2
A. x=-2是f(x)的极大值点
1
B. 当-2-4
2
C. 当 时,
00,
π
ω>0,|φ|≤ ).下列说法正确的有( )
2
π π
A. 求摩天轮转动一周的解析式H(t)=62sin( t- )+83
15 2
B. 游客甲坐上摩天轮后10分钟,距离地面的高度第一次恰好达到52米
C. 游客甲坐上摩天轮后,一段连续的5分钟时间内,高度变化最多可达62米
D. 若游客乙在游客甲之后进入座舱,且中间间隔5个座舱,从游客甲坐上摩天轮后
开始计时,17.5分钟后游客乙和游客甲距离地面的高度恰好首次相同
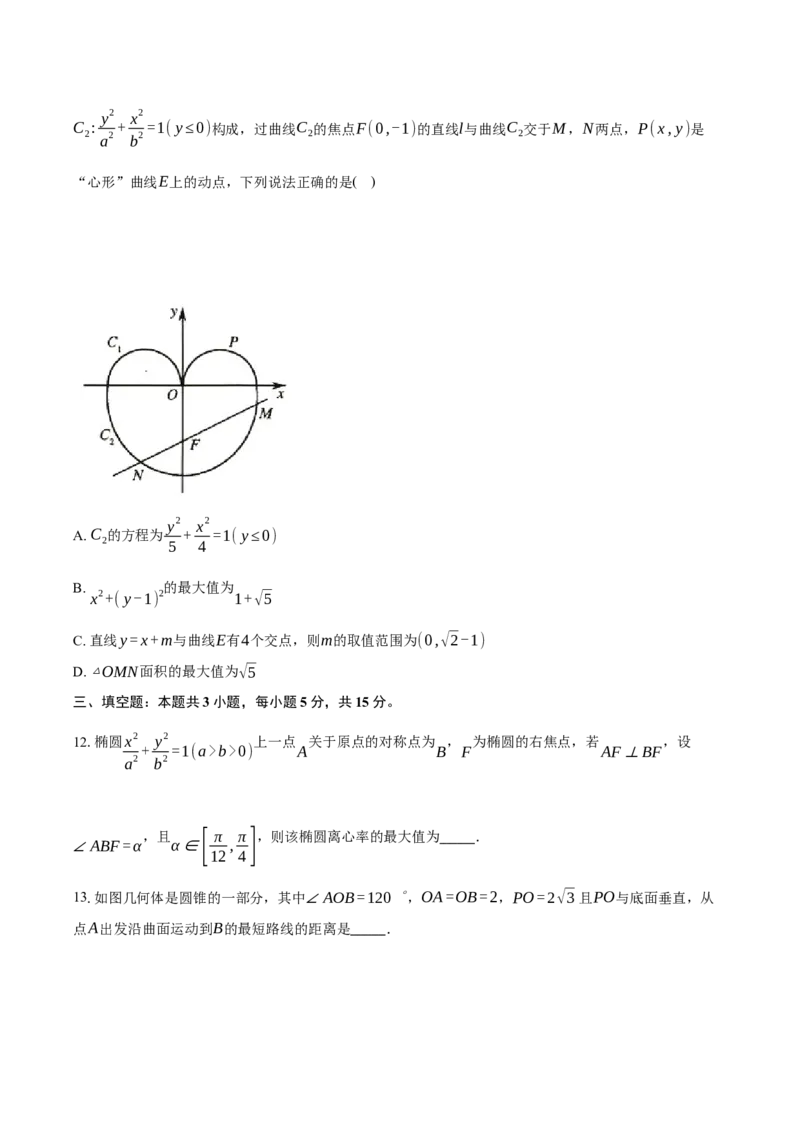
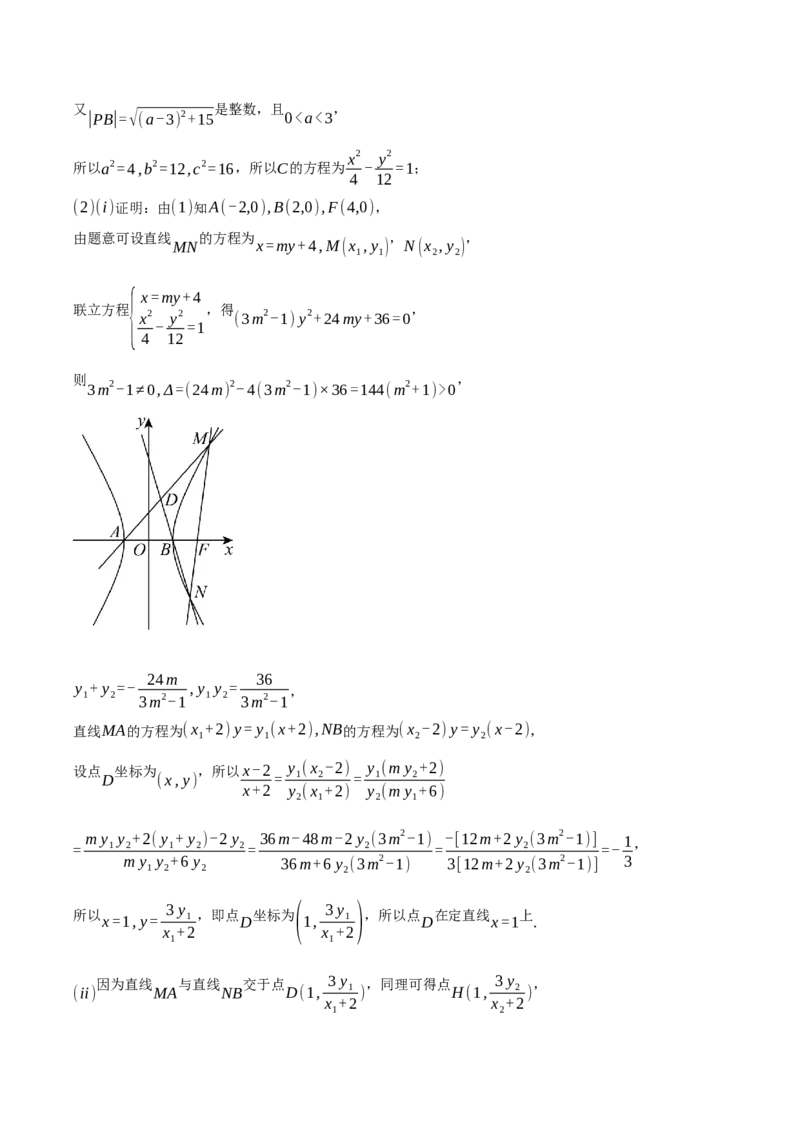
11.如图,类似“心形”的曲线E,可以看成由上部分曲线C :y=√-x2+2|x|,下部分曲线
1y2 x2
C : + =1(y≤0)构成,过曲线C 的焦点F(0,-1)的直线l与曲线C 交于M,N两点,P(x,y)是
2 a2 b2 2 2
“心形”曲线E上的动点,下列说法正确的是( )
y2 x2
A. C 的方程为 + =1(y≤0)
2 5 4
B. 的最大值为
x2+(y-1) 2 1+√5
C. 直线y=x+m与曲线E有4个交点,则m的取值范围为(0,√2-1)
D. △OMN面积的最大值为√5
三、填空题:本题共3小题,每小题5分,共15分。
12.椭圆x2 y2 上一点 关于原点的对称点为 , 为椭圆的右焦点,若 ,设
+ =1(a>b>0) A B F AF⊥BF
a2 b2
,且 [ π π],则该椭圆离心率的最大值为 .
∠ABF=α α∈ ,
12 4
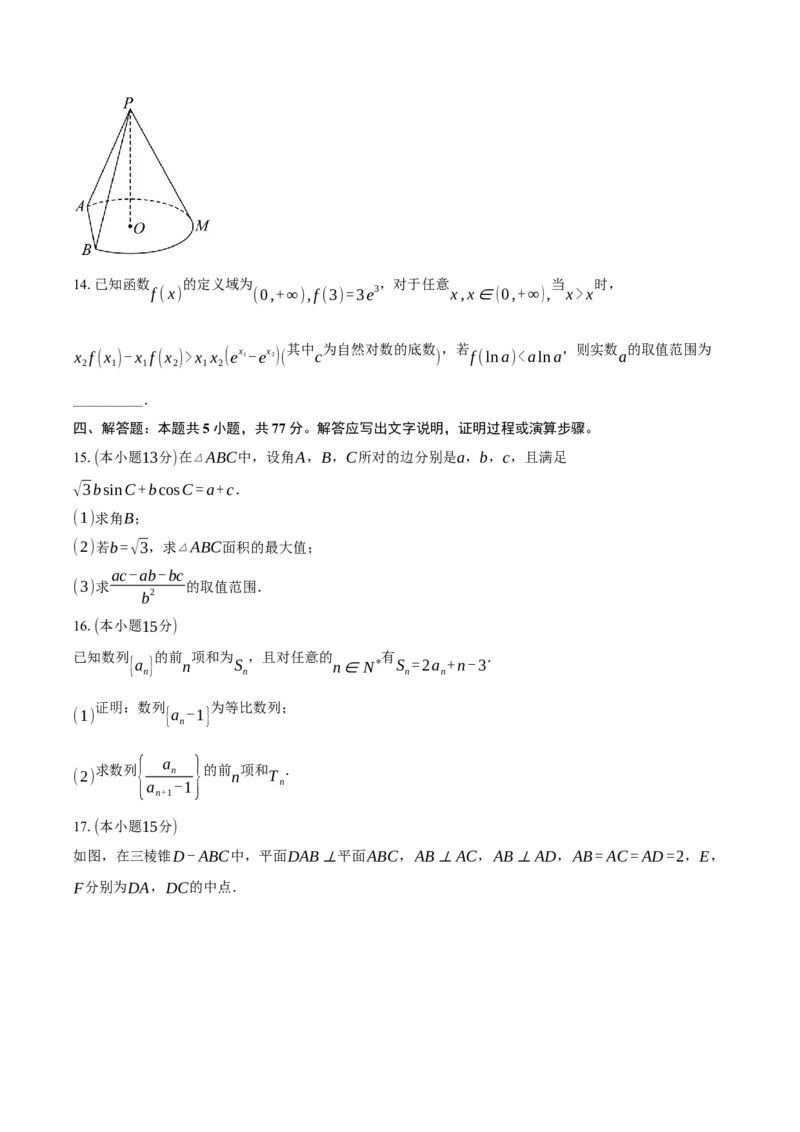
13.如图几何体是圆锥的一部分,其中∠AOB=120 ∘,OA=OB=2,PO=2√3 且PO与底面垂直,从
点A出发沿曲面运动到B的最短路线的距离是 .14.已知函数 的定义域为 ,对于任意 当 时,
f(x) (0,+∞),f(3)=3e3 x,x∈(0,+∞), x>x
其中 为自然对数的底数 ,若 ,则实数 的取值范围为
x f (x )-x f (x )>x x (ex 1-ex 2)( c ) f(lna)0,b>0) A,B C 、 F C
a2 b2
|PB|=|PF|,且|PB|是整数.
(1)求双曲线C的方程;
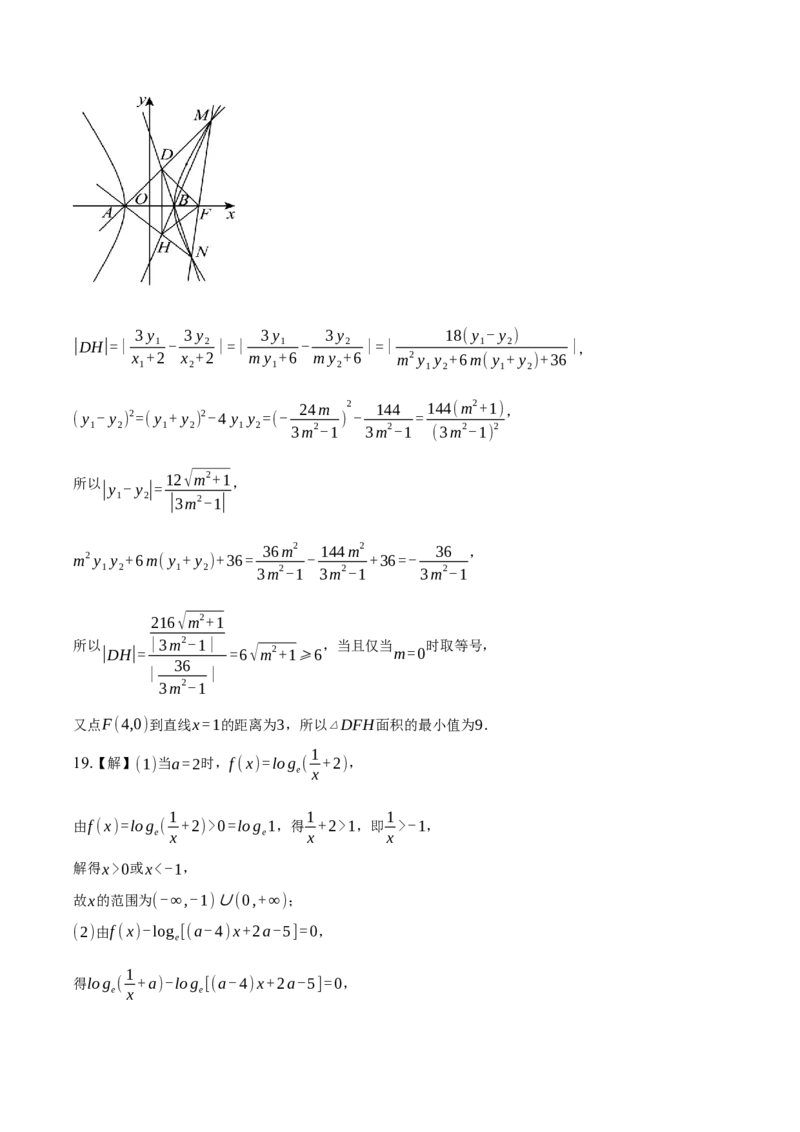
(2)设过点F的直线与C的右支交于M,N两点,直线MA与直线NB交于点D.
(i)证明:点D在定直线上; (ii)若直线MB与直线NA交于点H,求▵DFH面积的最小值.
19.(本小题17分)
1
已知a∈R,函数f(x)=log ( +a).(其中e=2.71828)
e x
(1)当a=2时,解不等式f(x)>0;
(2)若关于x的方程f(x)-log [(a-4)x+2a-5]=0的解集中恰有一个元素,求a的取值范围;
e
1
(3)设a>0,若对任意t∈[ ,1],函数f(x)在区间[t,t+1]上的最大值与最小值的差不超过ln2,求a的
2
取值范围.答案
1.A 2.B 3.B 4.D 5.B 6.D 7.C 8.C 9.ABD 10.ACD 11.AC
√6
12. 13.4√3 14.(1,e3)
3
15.【解】(1)因为√3bsinC+bcosC=a+c,
根据正弦定理得:√3sinBsinC+sinBcosC=sin A+sinC,
且sin A=sin(B+C)=sinBcosC+cosBsinC,
可得√3sinBsinC+sinBcosC=sinBcosC+cosBsinC+sinC,
即√3sinBsinC-cosBsinC=sinC,
又因为C∈(0,π),则sinC≠0,
π 1
可得√3sinB-cosB=1,整理可得sin(B- )= ,
6 2
π π 5π
且B∈(0,π),则B- ∈(- , ),
6 6 6
π π π
可得B- = ,解得B= ;
6 6 3
1
(2)由余弦定理得:b2=a2+c2-2accosB,即3=a2+c2-2ac× ,
2
可得a2+c2=3+ac⩾2ac,解得ac⩽3,
当且仅当a=c=√3时等号成立,
1 √3 3√3
所以△ABC的面积:S = acsinB= bc⩽ ,
△ABC 2 4 4
3√3
故△ABC面积的最大值为 ;
4
π
(3)由(1)得B= ,
3
ac-ab-bc sinAsinC-sinAsinB-sinBsinC
根据正弦定理得: =
b2 sin2B
4 √3 √3
= [sin Asin(A+B)- sin A- sin(A+B)]
3 2 2
4 √3 1 3 3√3
= ( sin AcosA+ sin2A- cosA- sin A)
3 2 2 4 4
√3 1 1
= sin2A- cos2A-cosA-√3sin A+
3 3 32 π π 1
= sin(2A- )-2sin(A+ )+ ,
3 6 6 3
π π π
令x=A+ ,则2A- =2x- ,
6 6 2
π π
可得sin(2A- )=sin(2x- )=-cos2x=2sin2x-1,
6 2
ac-ab-bc 2 1 4 1
将原式化为: = (2sin2x-1)-2sinx+ = sin2x-2sinx- ,
b2 3 3 3 3
2π π π 5π 1
因为A∈(0, ),则x=A+ ∈( , ),可得sinx∈( ,1],
3 6 6 6 2
根据二次函数的图象性质得到,
当 3时,原式取得最小值,ac-ab-bc 4 3 2 3 1 13;
sinx= = ×( ) -2× - =-
4 b2 3 4 4 3 12
ac-ab-bc 4 1
当sinx=1时,原式取得最大值, = ×12-2×1- =-1;
b2 3 3
ac-ab-bc 13
故 的取值范围为:[- ,-1].
b2 12
16. (1)证明:当n=1时,a =S =2a -2,解得a =2,
1 1 1 1
当n⩾2时,a =S -S =2a -2a +1,
n n n-1 n n-1
整理得 ,即 ,
a =2a -1 a -1=2(a -1)
n n-1 n n-1
又因为a -1=1≠0,
1
所以{a -1}是以1为首项,2为公比的等比数列.
n
由 可得 ,即 ,
(2) (1) a -1=(a -1)qn-1=2n-1 a =2n-1+1
n 1 n
则 a 2n-1+1 1 1 ,
n = = +
a -1 2n 2 2n
n+1
1 1 1 1 1 1 1 1 1 1 1 1
故T =( + )+( + )+⋯+( + )=( + +⋯+ )+( + +⋯+ )
n 2 2 2 22 2 2n 2 2 2 2 22 2n1
1-
n 1 2n n+2 1
= + × = - .
2 2 1 2 2n
1-
2
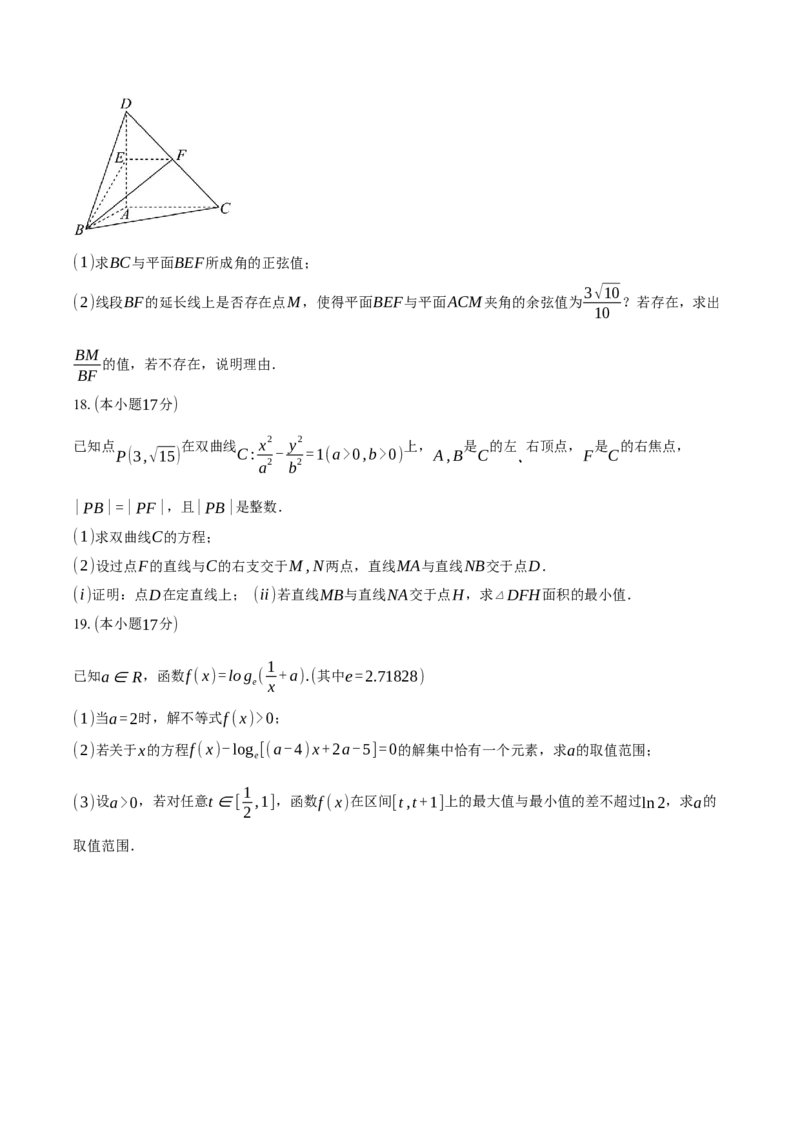
17.【解】(1)因为平面 DAB⊥ 平面 ABC ,平面 DAB∩ 平面 ABC=AB , AB⊥AC , AC⊂ 平
面 ABC ,
所以 AC⊥ 平面 DAB ,
因为 AB,AD⊂ 平面 DAB ,
所以 AC⊥AB , AC⊥AD ,
又AB⊥AD,
因为 ,所以 .
AB=AC=2 BC=√AC2+AB2=2√2
以A为原点,AB、AC、AD为 x,y,z 轴正方向建系,如图所示,
则 B(2,0,0),E(0,0,1),C(0,2,0),F(0,1,1) ,
所以 ⃗ ⃗ ⃗ ,
BC=(-2,2,0),BE=(-2,0,1),BF=(-2,1,1)
设平面 的法向量 ⃗ ,
BEF n=(x,y,z)
{⃗ ⃗
则 n⋅BE=0 ,即 {-2x+z=0 ,
⃗ ⃗ -2x+ y+z=0
n⋅BF=0
令
x=1
,则
z=2,y=0
,所以 ⃗
n=(1,0,2)
,
设 BC 与平面 BEF 所成角为 θ ,
则 | ⟨⃗ ⃗ ⟩| |-2| √10 ,
sinθ= cos n,BC = =
√8×√5 10√10
所以 BC 与平面 BEF 所成角的正弦值 .
10
BM
(2)假设存在点M,设
BF
=λ(λ>1) ,则
B
⃗
M=λB
⃗
F=(-2λ,λ,λ)
,
所以 ⃗ ⃗ ⃗ , ⃗ ,
AM=AB+BM=(2-2λ,λ,λ) AC=(0,2,0)
设平面
ACM
的法向量
m
⃗
=(x ,y ,z )
,
1 1 1
则 { m ⃗ ⋅A ⃗ M=0 ,即 {(2-2λ)x +λ y +λz =0 ,
1 1 1
⃗ ⃗ 2y =0
m⋅AC=0 1
令 ,则 λ ,即 ⃗ ( λ ) ,
z =1 x = ,y =0 m= ,0,1
1 1 2λ-2 1 2λ-2
| λ |
+2
⟨⃗ ⃗⟩ 2λ-2 3√10
所以 cos m,n = = ,
√ ( λ ) 2 10
+1⋅√5
2λ-2
整理得 ( λ ) 2 8λ ,解得 λ 或 1 ,
7 - +1=0 =1
2λ-2 2λ-2 2λ-2 7
2
所以 λ=2 或 λ=- (舍),
5
3√10 BM
所以存在点M使得平面 BEF 与平面 ACM 夹角的余弦值为 ,且 =2 .
10 BF
18.【解】(1)设C的右顶点B(a,0),右焦点F(c,0),
9 15
由P(3,√15),|PB|=|PF|,得a+c=6,又c2=a2+b2, - =1,
a2 b2又 是整数,且 ,
|PB|=√(a-3) 2+15 00
24m 36
y + y =- ,y y = ,
1 2 3m2-1 1 2 3m2-1
直线MA的方程为(x +2)y= y (x+2),NB的方程为(x -2)y= y (x-2),
1 1 2 2
设点 坐标为 ,所以x-2 y (x -2) y (my +2)
D (x,y) = 1 2 = 1 2
x+2 y (x +2) y (my +6)
2 1 2 1
=
m y
1
y
2
+2(y
1
+ y
2
)-2y
2=
36m-48m-2y
2
(3m2-1)
=
-[12m+2y
2
(3m2-1)]
=-
1,
m y y +6 y 36m+6 y (3m2-1) 3[12m+2y (3m2-1)] 3
1 2 2 2 2
3 y 3 y
所以 x=1,y= 1 ,即点 D 坐标为( 1, 1 ),所以点 D 在定直线 x=1 上 .
x +2 x +2
1 1
因为直线 与直线 交于点 3 y ,同理可得点 3 y ,
(ii) MA NB D(1, 1 ) H(1, 2 )
x +2 x +2
1 23 y 3 y 3 y 3 y 18(y - y )
|DH|=| 1 - 2 |=| 1 - 2 |=| 1 2 |
,
x +2 x +2 m y +6 m y +6 m2y y +6m(y + y )+36
1 2 1 2 1 2 1 2
(y - y ) 2=(y + y ) 2-4 y y =(-
24m
)
2
-
144
=
144(m2+1),
1 2 1 2 1 2 3m2-1 3m2-1 (3m2-1) 2
所以
12√m2+1,
|y - y |=
1 2 |3m2-1|
36m2 144m2 36 ,
m2y y +6m(y + y )+36= - +36=-
1 2 1 2 3m2-1 3m2-1 3m2-1
216√m2+1
所以 |3m2-1| ,当且仅当 时取等号,
|DH|= =6√m2+1⩾6 m=0
36
| |
3m2-1
又点F(4,0)到直线x=1的距离为3,所以▵DFH面积的最小值为9.
1
19.【解】(1)当a=2时,f(x)=log ( +2),
e x
1 1 1
由f(x)=log ( +2)>0=log 1,得 +2>1,即 >-1,
e x e x x
解得x>0或x<-1,
故x的范围为(-∞,-1)∪(0,+∞);
(2)由f(x)-log [(a-4)x+2a-5]=0,
e
1
得log ( +a)-log [(a-4)x+2a-5]=0,
e x e1
即log ( +a)=log [(a-4)x+2a-5],
e x e
1
即 +a=(a-4)x+2a-5>0,①.
x
则 ,
(a-4)x2+(a-5)x-1=(x+1)[(a-4)x-1]=0 ②
当a=4时,②的解为x=-1,代入①成立.
当a=3时,②的解为x=-1,代入①成立.
1
当a≠4且a≠3时,②的解为x=-1或x= ,
a-4
1
若x=-1是方程①的解,则 +a=a-1>0,即a>1,
x
1 1
若x= 是方程①的解,则 +a=2a-4>0,即a>2,
a-4 x
要使①有且仅有一个解,则1