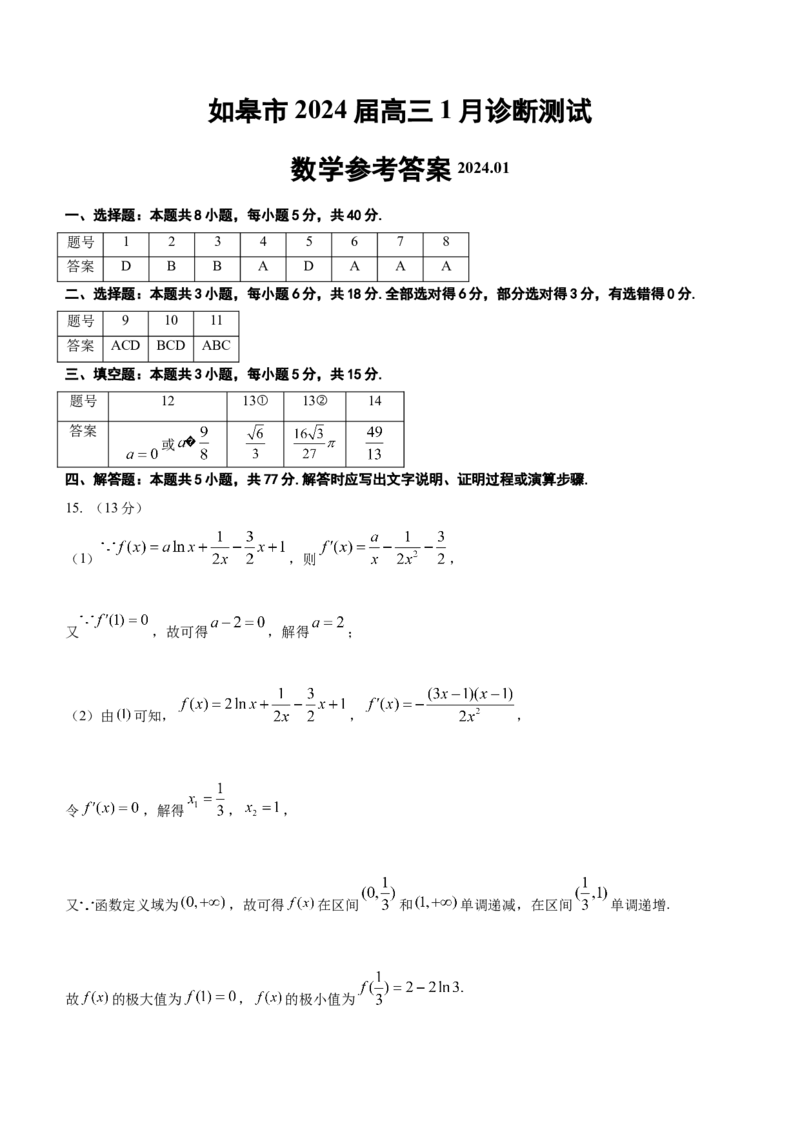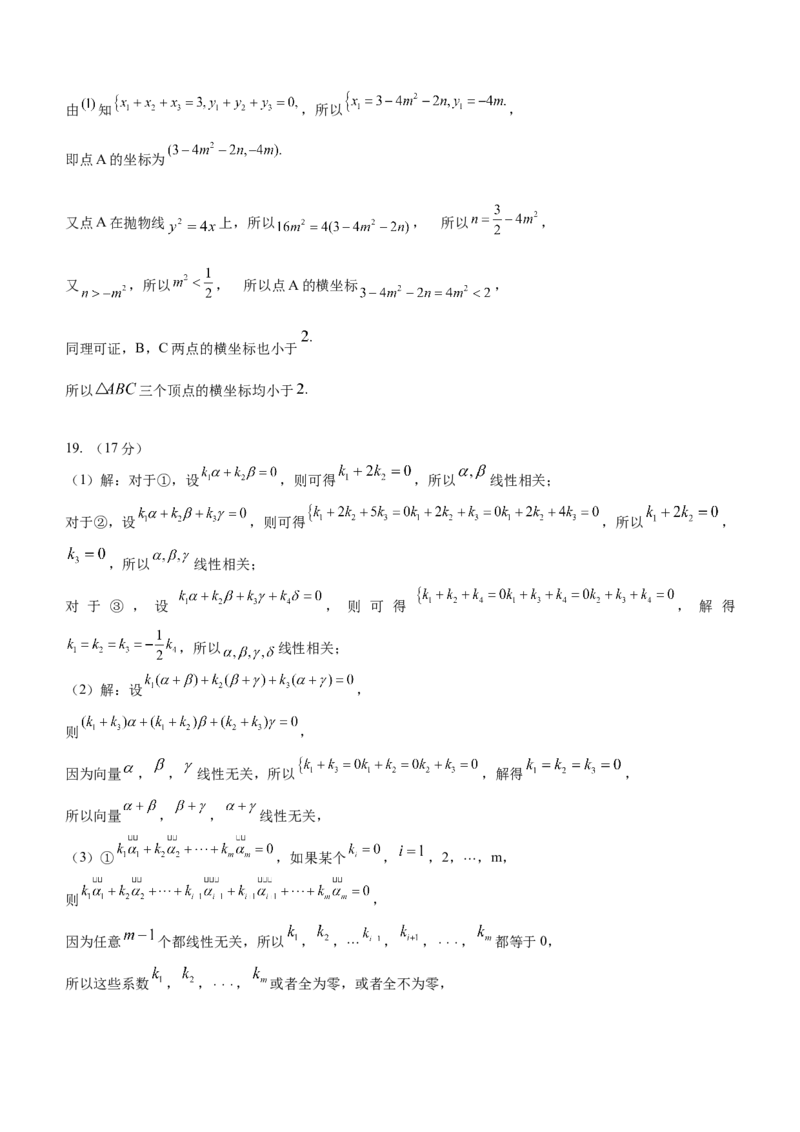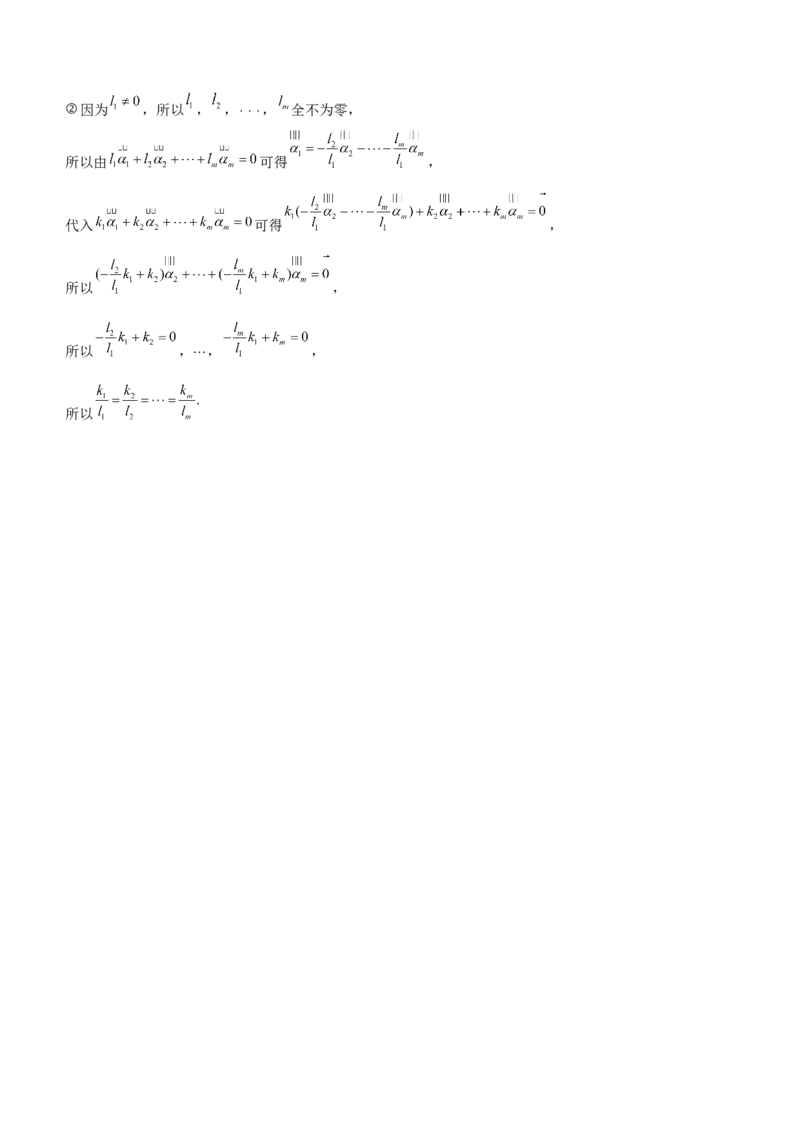文档内容
如皋市 2024 届高三 1 月诊断测试
数学参考答案
2024.01
一、选择题:本题共8小题,每小题5分,共40分.
题号 1 2 3 4 5 6 7 8
答案 D B B A D A A A
二、选择题:本题共3小题,每小题6分,共18分.全部选对得6分,部分选对得3分,有选错得0分.
题号 9 10 11
答案 ACD BCD ABC
三、填空题:本题共3小题,每小题5分,共15分.
题号 12 13① 13② 14
答案
或
四、解答题:本题共5小题,共77分.解答时应写出文字说明、证明过程或演算步骤.
15. (13分)
(1) ,则 ,
又 ,故可得 ,解得 ;
(2)由 可知, , ,
令 ,解得 , ,
又 函数定义域为 ,故可得 在区间 和 单调递减,在区间 单调递增.
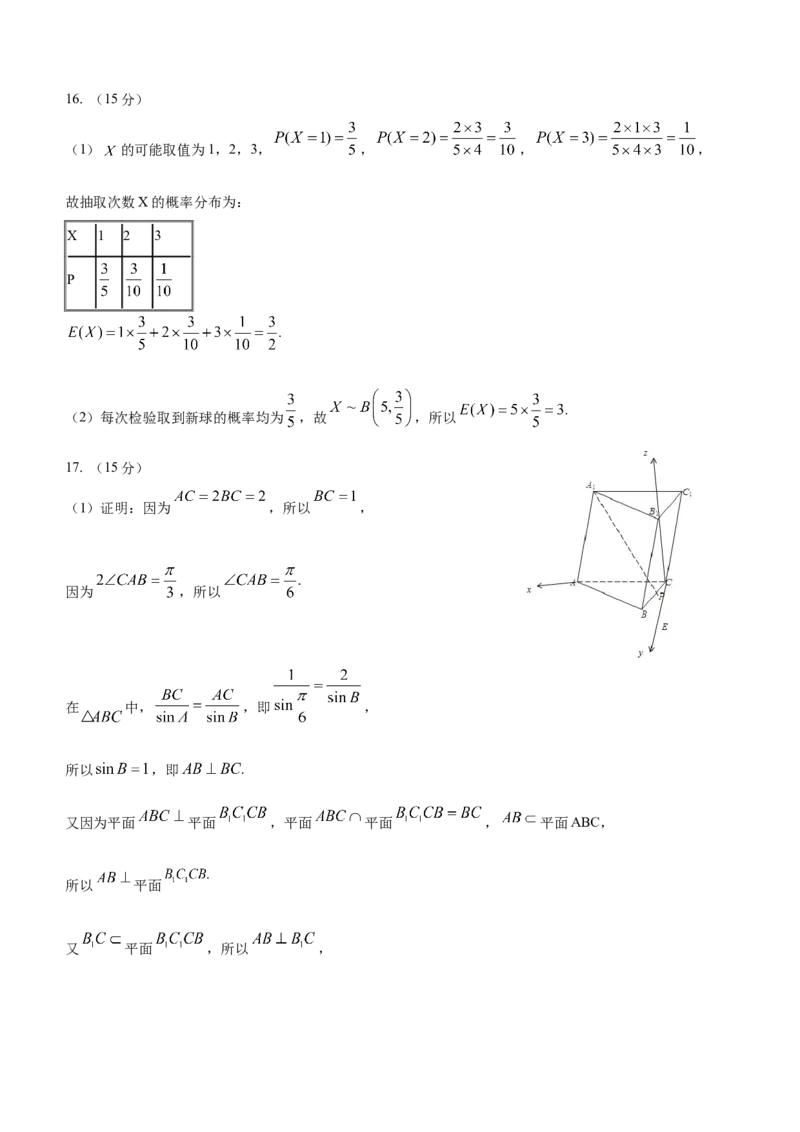
故 的极大值为 , 的极小值为16. (15分)
(1) 的可能取值为1,2,3, , , ,
故抽取次数X的概率分布为:
X 1 2 3
P
(2)每次检验取到新球的概率均为 ,故 ,所以
17. (15分)
(1)证明:因为 ,所以 ,
因为 ,所以
在 中, ,即 ,
所以 ,即
又因为平面 平面 ,平面 平面 , 平面ABC,
所以 平面
又 平面 ,所以 ,在 中, , , ,
所以 ,即 ,
所以
而 , 平面ABC, 平面ABC, ,
所以 平面
又 平面 ,所以平面 平面
(2)在平面ABC中过点C作AC的垂线CE,
以C为坐标原点,分别以CA,CE, 所在直线为x,y,z轴建立如图所示的空间直角坐标系,
则 , , , ,
所以 , ,
所以 ,
平面 的一个法向量为 ,
设直线 与平面 所成的角为 ,
则直线 与平面 所成角的正弦值为:,
18. (17分)
(1)解:设直线 AB 的方程为 ,与 联立得 , ,得
,设 , , ,则 , ,
所以 ,
由题意知 ,因为 , , , ,
所以 ,
所以 ,
所以 ,即点C的坐标为 , 代入抛物线E的方程得: ,解得 ,
满足条件 ,
所以直线AB的方程为
(2)证明:设直线BC的方程为 ,与 联立得 ,
,所以 , , ,
所以由 知 ,所以 ,
即点A的坐标为
又点A在抛物线 上,所以 , 所以 ,
又 ,所以 , 所以点A的横坐标 ,
同理可证,B,C两点的横坐标也小于
所以 三个顶点的横坐标均小于
19. (17分)
(1)解:对于①,设 ,则可得 ,所以 线性相关;
对于②,设 ,则可得 ,所以 ,
,所以 线性相关;
对 于 ③ , 设 , 则 可 得 , 解 得
,所以 线性相关;
(2)解:设 ,
则 ,
因为向量 , , 线性无关,所以 ,解得 ,
所以向量 , , 线性无关,
(3)① ,如果某个 , ,2,⋯,m,
则 ,
因为任意 个都线性无关,所以 , ,⋯ , ,⋅⋅⋅, 都等于0,
所以这些系数 , ,⋅⋅⋅, 或者全为零,或者全不为零,②因为 ,所以 , ,⋅⋅⋅, 全不为零,
所以由 可得 ,
代入 可得 ,
所以 ,
所以 ,⋯, ,
所以