数学2026届高三高考模拟调研（一）答案(1)_2026年1月_2601072026年重庆市高三康德高考模拟调研卷（一）（全科）

数学（一）参考答案 一、选择题： 1～8 BCAC ADDC 1题解析：因为ab2(1)120，所以a b，|a||b| 5 ，ab(1,3)； 2题解析：集合A满足0即a2 40，所以A(,2][2,) ，B [1,3]，则AB [2,3]； 3题解析：由 y  f (x)的图象向左平移2个单位，得到 y  f (x2)的图象；再关于 y轴对称，得到 y  f (x2) 1 的图象；最后纵坐标不变，----------------横坐标压缩为原来的 ，得到 y  f (2x2)的图象．将 2 上述过程逆向变换，即可由 y  f (2x2)的图象得到y  f (x)的图象． |a| 4题解析：由直线与圆相切则有圆心到直线的距离等于半径，所以有 1，得a 2； 13 5题解析：设底面边长为a，取AB的中点为E，P在底面的射影为底面ABCD的中心O，所以侧面与底面所 P 7 a EO 7 成角为PEO，则PE  a，EO  ，所以cosPEO  ； 2 2 PE 7 B C sincoscossin4sinsin O E 6题解析：tantan4tantan coscos D A 4 4sinsin sin()4sinsin 5 4(cos()sinsin)     4； coscos coscos coscos 3 2 18 7题解析：总体平均分为z  4 3 ，记男生方差为s2 1，平均分为x 4，女生方差为s2 1，平 5 5 5 x y 3 2 31 均分为 y 4，----------------则总体方差s2  [s2 (x z)2] [s2 (y z)2] ； 5 x 5 y 25 8题解析：函数 f(x)存在两个零点，即mex lnmln(x1)1有两个解，方程两边同时加上x，则有 mex lnmx ln(x1)(x1) 即ln(mex)mex ln(x1)(x1) ，设函数g(x)lnxx，则 x1 有g(mex) g(x1)，公众号雾都资料库因为g(x)是单调递增函数，则有mex  x1m 有 ex x1 两个解，所以根据h(x) 的函数图象知m(0,1)． ex 二、选择题： 9．ACD 10．BC 11．BCD n(3n21) 9题解析：由a a 5d 15d 3，则a a (n2)d 3n12，S  ，所以选ACD； 7 2 n 2 n 2 10题解析：z z (m2i)(3ni)3m2n(6mn)i ，若z z 为纯虚数，则有3m2n0，即3m2n， 1 2 1 2 A 错误； z m2i=3ni z ，所以 m3,n2 ， z  m24  13 ，B 正确； 1 2 1 关注公众号 高第中1试页卷共君5 第页1/7页 下载更多学习资料z z (m3)(2n)i，若 z z  2，则(m3)2 (n2)2 4，则|mni| m2n2 最 1 2 1 2 大 值 为 圆 心 (3,2) 到 原 点 的 距 离 与 半 径 的 和 132 ， C 正 确 ； 若 z z  2 ， 1 2 (m3)2 (n2)2 2，----------------则点(m,n)在圆心为(3,2)，半径为 2 的圆上，设直线 |5a| mna，则圆心到直线的距离d   2 ，解得3a7，所以mn的取值范围为[3,7]． 2 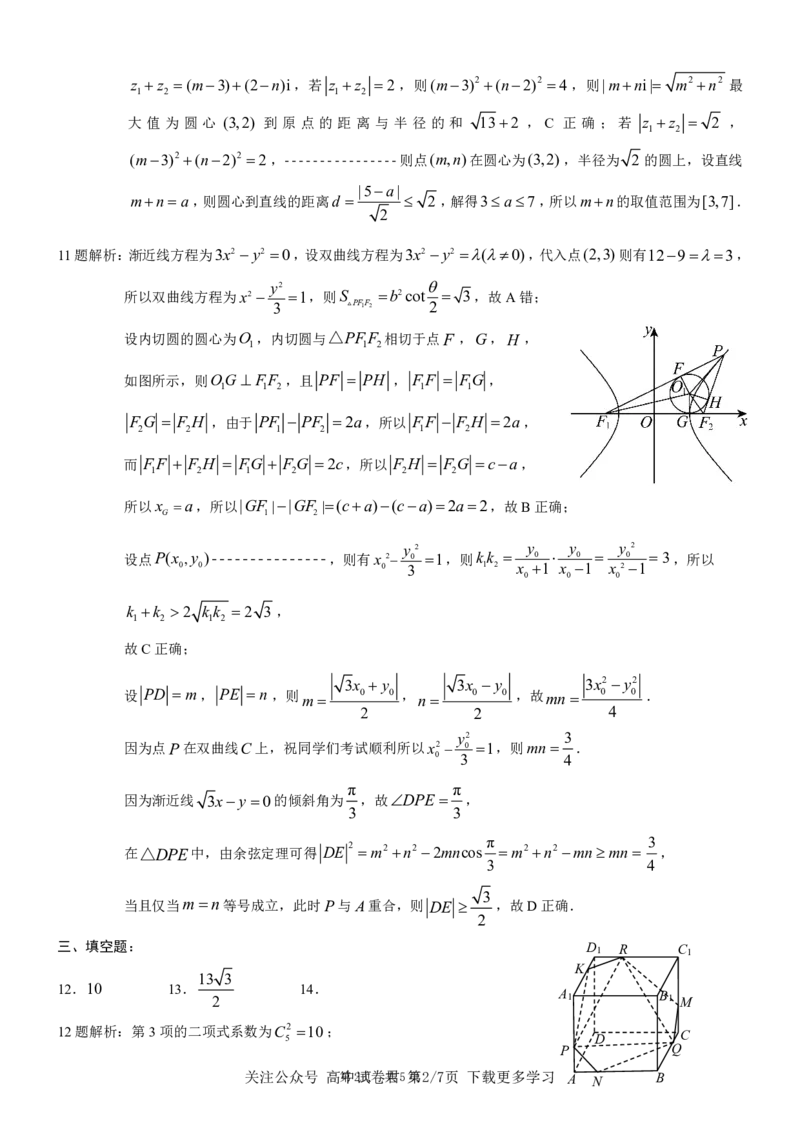11题解析：渐近线方程为3x2  y2 0，设双曲线方程为3x2 y2 (0)，代入点(2,3)则有1293， y2  所以双曲线方程为x2  1，则S b2cot  3，故A错； 3 PF1F2 2 设内切圆的圆心为O ，内切圆与△PFF 相切于点F ，G，H ， 1 1 2 如图所示，则OG FF ，且 PF  PH ， FF  FG ， 1 1 2 1 1 FG  F H ，由于 PF  PF 2a，所以 FF  F H 2a， 2 2 1 2 1 2 而 FF  F H  FG  FG 2c，所以 F H  FG ca， 1 2 1 2 2 2 所以x a，所以|GF ||GF |(ca)(ca)2a2，故B正确； G 1 2 y 2 y y y 2 设点P(x ,y )---------------，则有x 2 0 1，则kk  0  0  0 3，所以 0 0 0 3 1 2 x 1 x 1 x 21 0 0 0 k k  2 k k  2 3 ， 1 2 1 2 故C正确； 3x  y 3x  y 3x2 y2 设 PD  m， PE n，则 m 0 0 ， n 0 0 ，故mn 0 0 ． 2 2 4 y2 3 因为点P在双曲线C上，祝同学们考试顺利所以x2  0 1，则mn ． 0 3 4 π π 因为渐近线 3xy0的倾斜角为 ，故DPE  ， 3 3 π 3 在△DPE中，由余弦定理可得 DE 2 m2 n2 2mncos m2 n2 mnmn ， 3 4 3 当且仅当mn等号成立，此时P与A重合，则 DE  ，故D正确． 2 三、填空题： D 1 R C 1 K 13 3 12．10 13． 14． 2 A 1 B 1 M 12题解析：第3项的二项式系数为C 5 2 10； D C P Q 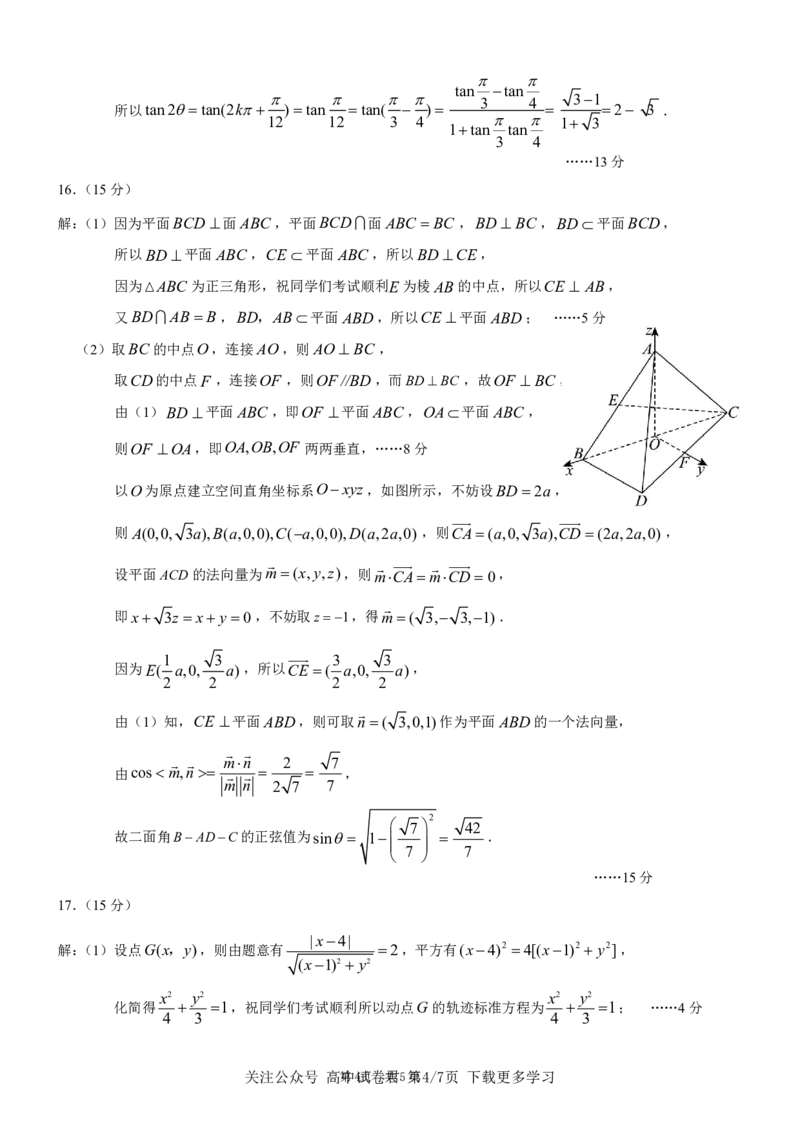关注公众号 高第中2试页卷共君5 第页2/7页 下载更多学习资 A 料 N B13题解析：设该截面分别与棱CC ，AB，AD 相交于点M ，N ，K， 1 1 1 则CM  AN  DK 1，截面PNQMRK 满足PN QM  RK  2，NQ MR KP  2 2 ， 1 1 1 6 13 3 且PM 3 2 ．S S S  ( 23 2) 6 (2 23 2)  ． PNQMRK 梯形PNQM 梯形PKRM 2 2 2 2 14题解析：甲在一局中获胜的概率为分甲先答题甲获胜 1 1 1 1 1 2 1 2 1 7 p           ， 1 2  2 2 2 2 3 2 3 2   24 1 1 2 1 2 1 2 1 2 1 和祝同学们考试顺利乙先答题而甲获胜概率为 p           ， 2 2  3 3 2 3 2 3 2 3   3 15 5 所以甲一局获胜概率为 p  p   ， 1 2 24 8 甲在一场比赛中获胜分为胜前两局+胜一三局+胜后两局，所以 175 P 2 (1)(1)2  ． 256 四、解答题： 15．（13分）    解：（1） f(x) 6sin(x ) 2sin(x  ) 4 4 2    6sin(x ) 2cos(x ) 4 4 3  1  2 2( sin(x ) cos(x )) 2 4 2 4 5 2 2sin(x ) ……4分 12 2 因为函祝同学们考试顺利数的最小正周期为，所以 ，则有2， ……6分  5 所以 f  x 2 2sin(2x )； 12 5 k 5 由2x k，则有x  ， 12 2 24 k 5 所以函数 f(x)的对称中心为(  ,0),kZ； ……8分 2 24 5 5 （2）由 f()2 2sin(2 )2 2 ，所以sin(2 ) 1， 12 12 5   则有2 2k ，即22k ， 12 2 12 关注公众号 高第中3试页卷共君5 第页3/7页 下载更多学习资料  tan tan     3 4 31 所以tan2tan(2k )tan tan(  )  2 3 ． 12 12 3 4   1 3 1tan tan 3 4 ……13分 16．（15分） 解：（1）因为平面BCD 面ABC，平面BCD面ABC  BC ，BD  BC，BD平面BCD， 所以BD 平面ABC，CE 平面ABC，所以BD CE， 因为ABC为正三角形，祝同学们考试顺利E为棱AB的中点，所以CE  AB， 又BDAB B，BD，AB平面ABD，所以CE 平面ABD； ……5分 （2）取BC的中点O，连接AO，则AO  BC ， 取CD的中点F ，连接OF ，则OF//BD，而BDBC ，故OF  BC， 由（1）BD 平面ABC，即OF 平面ABC，OA平面ABC， 则OF OA，即OA,OB,OF 两两垂直，……8分 以O为原点建立空间直角坐标系Oxyz，如图所示，不妨设BD 2a，   则A(0,0, 3a),B(a,0,0),C(a,0,0),D(a,2a,0) ，则CA(a,0, 3a),CD (2a,2a,0)，      设平面ACD的法向量为m(x,y,z)，则mCAmCD  0，  即x 3z  x y 0，不妨取z1，得m( 3, 3,1)． 1 3  3 3 因为E( a,0, a)，所以CE ( a,0, a)， 2 2 2 2  由（1）知，CE 平面ABD，则可取n ( 3,0,1)作为平面ABD的一个法向量，     mn 2 7 由cosm,n      ， m n 2 7 7 2  7  42 故二面角BADC的正弦值为sin 1   ．   7 7   ……15分 17．（15分） |x4| 解：（1）设点G(x，y)，则由题意有 2，平方有(x4)2 4[(x1)2  y2]， (x1)2  y2 x2 y2 x2 y2 化简得  1，祝同学们考试顺利所以动点G的轨迹标准方程为  1； ……4分 4 3 4 3 关注公众号 高第中4试页卷共君5 第页4/7页 下载更多学习资料1 3 （2）先考察直线 y0，此时P(2,0),Q(2,0)，且k k   1，该直线满足题意， 1 2 2 2 若该定点存在，则必在x轴上，记为K(a,0) xmya  设l 为xmya，祝同学们考试顺利联立直线l 与椭圆C的方程x2 y2 ， 1 1   1  4 3 得(3m2 4)y2 6amy3a2 120 ， 6am 3a2 12 则36m2a2 4(3m2 4)(3a2 12)0，且有 y  y  ， y y  ， 1 2 3m2 4 1 2 3m2 4 3 3 3 3 y  y  y  y  所以k k  1 2  2 2  1 2  2 2 1 2 x 1 x 1 my a1 my a1 1 2 1 2 3 2my y (a1 m)(y  y )3(a1) 1 2 2 1 2  1 m2y y m(a1)(y  y )(a1)2 1 2 1 2 9m2 (6a24)m12a12 解得 1， 9m2 4a2 8a4 对应系数成比例，所以a4，所以该定点为K(4,0)． ……15分 18．（17分） 解：（1）①第一阶段12个小组，每组4支球队两两比赛，共有12C2 72场 4 ②第二阶段从32支球队淘汰到产生前四名，共有168428场 ③第三阶段，共有224场 所以，比赛总场数为72284104场； ……4分 （2）若有3名球员不在自己对应位置上C128， 4 祝同学们考试顺利若有4名球员不在自己对应位置上C1C1 9， 3 3 17 17 则4名球员至少有3名球员不在自己对应位置上的概率为 p   ； ……8分 A4 24 4 （3）A球队在小组三场比赛结束后的积分X可能取值为：0， 1， 2， 3， 4， 5， 6， 7， 9， 其中：0分(三负)、1分(一平两负)、2分(两平一负)、3分(一胜两负或三平)、 4分(一胜一平 一负)、5分(一胜两平)、6分(两胜一负)、7分(两胜一平)、9分(三胜) 1 1 1 1 P(X 0)    4 3 4 48 关注公众号 高第中5试页卷共君5 第页5/7页 下载更多学习资料1 1 1 1 1 1 1 1 1 1 P(X 1)          4 3 4 4 3 4 4 3 2 12 1 1 1 1 1 1 1 1 1 5 P(X 2)          4 3 4 4 3 2 4 3 2 48 1 1 1 1 1 1 1 1 1 1 1 1 1 P(X 3)             2 3 4 3 4 4 4 4 3 4 3 2 8 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 11 P(X 4)                   2 3 4 2 3 2 4 3 4 4 3 2 4 3 4 4 3 4 48 1 1 1 1 1 1 1 1 1 7 P(X 5)          2 3 2 4 3 2 4 3 4 48 1 1 1 1 1 1 1 1 1 5 P(X 6)          2 3 4 2 3 4 4 3 4 48 1 1 1 1 1 1 1 1 1 7 P(X 7)          2 3 2 2 3 4 4 3 4 48 1 1 1 1 P(X 9)    2 3 4 24 分布列为 X 0 1 2 3 4 5 6 7 9 1 1 5 1 11 7 5 7 1 P 48 12 48 8 48 48 48 48 24 1 5 1 11 7 5 7 1 13 期望E(X)1 2 3 4 5 6 7 9  ．……17分 12 48 8 48 48 48 48 24 3 19．（17分） 1 ax1 解：（1）对 f(x)求导有 f(x)a  （x0）， x x ①当a0时： f(x)0，故 f(x)在(0,)单调递减； 1 1 ②当a0时： f(x)在(0, )单调递减，在( ,)单调递增； ……5分 a a lnx1 lnx1 lnx （2） f(x)0a ，令g(x) ，则有g(x) ， x x x2 则有g(x)在(0,1)上单调递增，在(1,)单调递减． 若函数 f(x)存在两个零点，则不妨有0 x 1 x ，且有g(x ) g(x )， 1 2 1 2 要证x x 2，即证x 2x ，即证g(x ) g(2x)，即证g(x ) g(2x )， 1 2 2 1 2 1 1 1 lnx 1 ln(2x)1 即证 1  1 ，等价于(2x)lnx x ln(2x)22x 0， x 2x 1 1 1 1 1 1 1 令(x)(2x)lnxxln(2x)22x （0 x1）， 4 则有(x)ln[x(2x)] 4， x(2x) 关注公众号 高第中6试页卷共君5 第页6/7页 下载更多学习资料4 令u x(2x)，则有0u1，则(x)lnu 40， u 所以(x)在(0,1)上单调递增，祝同学们考试顺利所以(x)(1)0，得证；··········……11分 1 （3）a S S 2n(n2)，当n1时，a S 2符合a ，所以a 2n(nN ). n n n1 1 1 n n  设{b }公比为q，则有b 2qn1，即2qk12k2qk 恒成立，则q 0， n n lnk lnk 即有 lnq 恒成立． k k1 lnx lnx 分别令h(x) ，h (x) ， 1 x 2 x1 1lnx 则h  (x) ，所以h(x)在(0,e)上单调递增，在(e,)单调递减， 1 x2 1 x1xlnx h  (x) ，令s(x) x1xlnx，则s(x)lnx ，所以s(x)s(1)0，故h  (x)0， 2 x(x1)2 2 所以h (x)在(0,)上单调递减， 2 ln3 ln5 ①当k 5时： lnq ，解得 3 3q 4 5， 3 4 ln3 ln6 ②当k 6时： lnq ，解得 3 3q 5 6 （不成立）， 3 5 所以m的最大值为5． ……17分 关注公众号 高第中7试页卷共君5 第页7/7页 下载更多学习资料