2024届云南三校高考备考实用性联考卷（七）数学答案_2024年3月_013月合集_2024届云南三校高三下学期联考备考实用性联考（七）_2024届云南三校高三下学期联考备考实用性联考（七）数学

2024 届云南三校高考备考实用性联考卷（七） 数学参考答案 一、单项选择题（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只 有一项符合题目要求） 题号 1 2 3 4 5 6 7 8 答案 B A B C D C A C 【解析】 1．由A{x|1≤x≤0}，得 A{x|x1或x0}，而B{1，1，3，4}，依题意，阴影部 U 分表示的集合( A)B{1，3，4}，故选B． U 2．设 x2 axa0 的另一个根是 z ，易知 z 与1i 一定是共轭复数，故 z1i ，故 1i1i2，故选A．        1 π 3．由题知，|a|1，(ab)2 |a|2 2|a||b|cos|b|23，所以2cos1，cos ， ， 2 3 故选B． 4 4 16 9 4．由题意可知A：两人都没选择篮球，即P(A)   ，所以P(A)1P(A) ，而AB： 5 5 25 25 42 8 有 一 人 选 择 篮 球 ， 另 一 人 选 别 的 兴 趣 班 ， 则 P(AB)  ， 所 以 55 25 8 P(AB) 25 8 P(B|A)   ，故选C． P(A) 9 9 25 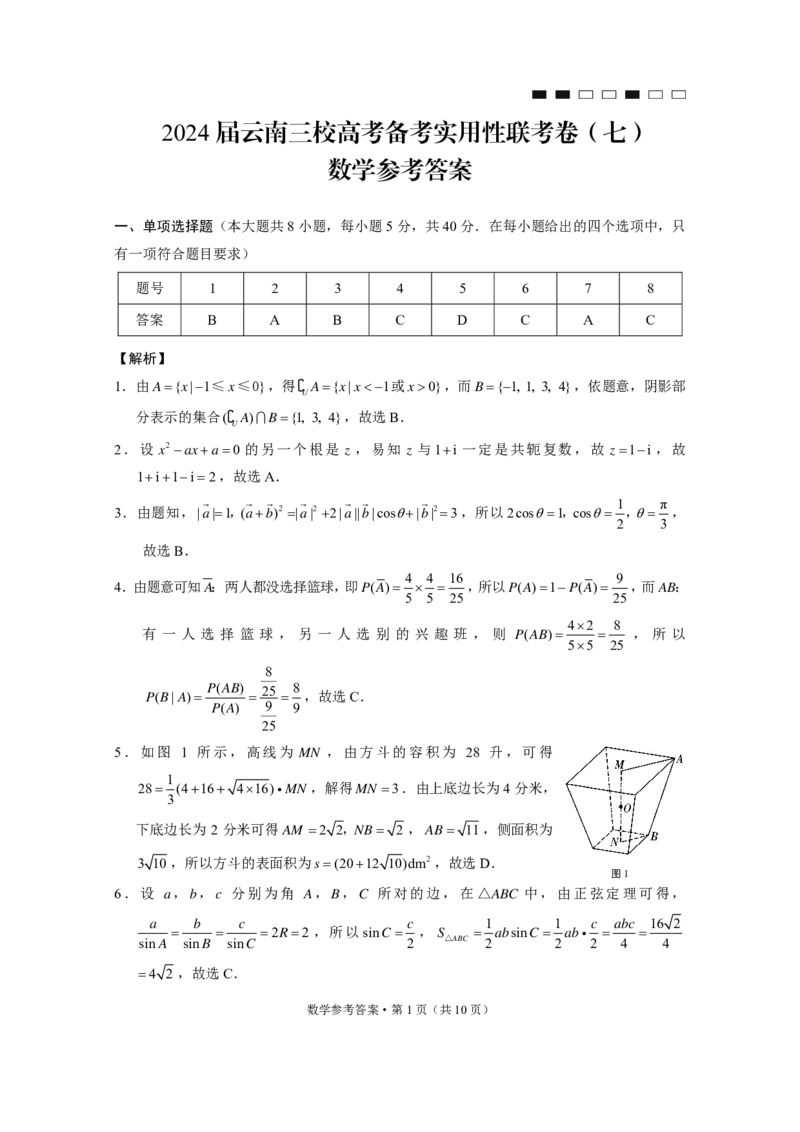5．如图 1 所示，高线为 MN ，由方斗的容积为 28 升，可得 1 28 (416 416)MN，解得MN 3．由上底边长为4分米， 3 下底边长为 2 分米可得AM 2 2，NB 2 ，AB 11，侧面积为 3 10，所以方斗的表面积为s(2012 10)dm2，故选D． 图1 6．设 a，b，c 分别为角 A，B，C 所对的边，在△ABC 中，由正弦定理可得， a b c c 1 1 c abc 16 2   2R2，所以sinC ， S  absinC ab   sinA sinB sinC 2 △ABC 2 2 2 4 4 4 2 ，故选C． 数学参考答案·第1页（共10页） {#{QQABbQCEogCAQJIAARhCAQmwCAKQkAGAAKoGhAAMIAAAyRFABAA=}#}7．根据已知条件有a 1，当n≥2时，a a 2，a a 3，a a 4，…，a a n， 1 2 1 3 2 4 3 n n1 以上各式累加得： a a 234n ，又 a 1，所以 a 1234n n 1 1 n n(n1) n(n1)  (n≥2) ， 经 检 验 a 1 符 合 上 式 ， 所 以 a  (nN*) ， 所 以 2 1 n 2 1 2 1 1   1   1 1 1 a  n(n1) 2 n  n1   ，设数列 a  的前n项和为S n ，则S n 2     1 2    2  3   n n 1 1 1 1  2 2 60  3  4    n  n1     2 n1 ，所以S 30 2 31  31 ，故选A． 8．根据题意， f(x)0，所以axex xlnx，令g(x)xex xlnx，x(0，e)，则函数 f(x)xex xlnxa 在 (0，e) 上 存 在 零 点 等 价 于 ya 与 g(x) 的 图 象 有 交 1 x1  1 (x1)(xex 1) 点．g(x)ex xex 1 ex(x1) (x1)ex   ，令h(x)xex x x  x x 1，x(0，e)，则h(x)ex xex 0，故h(x)在(0，e)上单调递增，因为h(0)10， 1 h(1)e10，所以存在唯一的x (0，1)，使得 h(x )0，即 x ex0 10，即ex0  ， 0 0 0 x 0 x lnx ，所以当0xx 时，h(x )0， g(x)0，g(x)单调递减，当x xe时， 0 0 0 0 0 h(x )0，g(x)0，g(x)单调递增，所以g(x)  g(x ) x ex0 x lnx 1x x 1， 0 min 0 0 0 0 0 0 又x0时，g(x)，故x(0，e)，g(x)[1，)，所以a≥1，故选C． 二、多项选择题（本大题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有 多项是符合题目要求的．全部选对的得6分，部分选对的得部分分，有选错的得0分） 题号 9 10 11 答案 AB AD ABD 【解析】 9．对于 A，由均值的性质可知E(X a)2 E(X )2 (a)2，由于a是不等于的常数， 故可得E(X a)2 E(X )2，即X 相对于的偏离程度小于X 相对于a的偏离程度，A 1 正确；对于B，根据方差公式s2  [(x x)2 (x x)2 (x x)2]，可知若一组数据x ， n 1 2 n 1 x ，…，x 的方差为0，则x x x ，B正确；对于C，由决定系数的定义可知，C 2 n 1 2 n 错误；对于 D，2的值变为原来的 10 倍，在相同的检验标准下，再去判断两变量的关联 性时，结论可能发生改变，D错误，故选AB． 数学参考答案·第2页（共10页） {#{QQABbQCEogCAQJIAARhCAQmwCAKQkAGAAKoGhAAMIAAAyRFABAA=}#}2 π π π 10．对A，由 f(0)1，得 2sin1，即sin ，又  ，∴ ，又 f(x) 2 2 2 4 π  π π π π π 的图象过点  ，0 ，则 f  0，即sin  0，∴  kπ，即得8k2， 8  8  8 4 8 4  π  5π kZ，又0≤2，∴2，所以 f(x) 2sin2x  2cos2x  ，故A正确；  4  4  5π  5π 5π 5π 5π 7π 对B，f   2cos2   2cos 0，故B错误；对C，当x  ，  时，  8   8 4  2  8 8  5π 5π  5π 7π 则2x  ，3π ，由余弦函数单调性知，f(x)在x ， 单调递减，故C错误；     4  2   8 8   5π 2 π π 对于D，由 f(x)1，得cos2x  ，解得x kπ或 kπ，kZ，方程 f(x)1  4  2 4 2 π π 5π 3π 9π 5π 13π 在(0，m)上有6个根，从小到大依次为： ， ， ， ， ， ，而第7个根为 ， 4 2 4 2 4 2 4 5π 13π 所以 m≤ ，故D正确，故选AD． 2 4 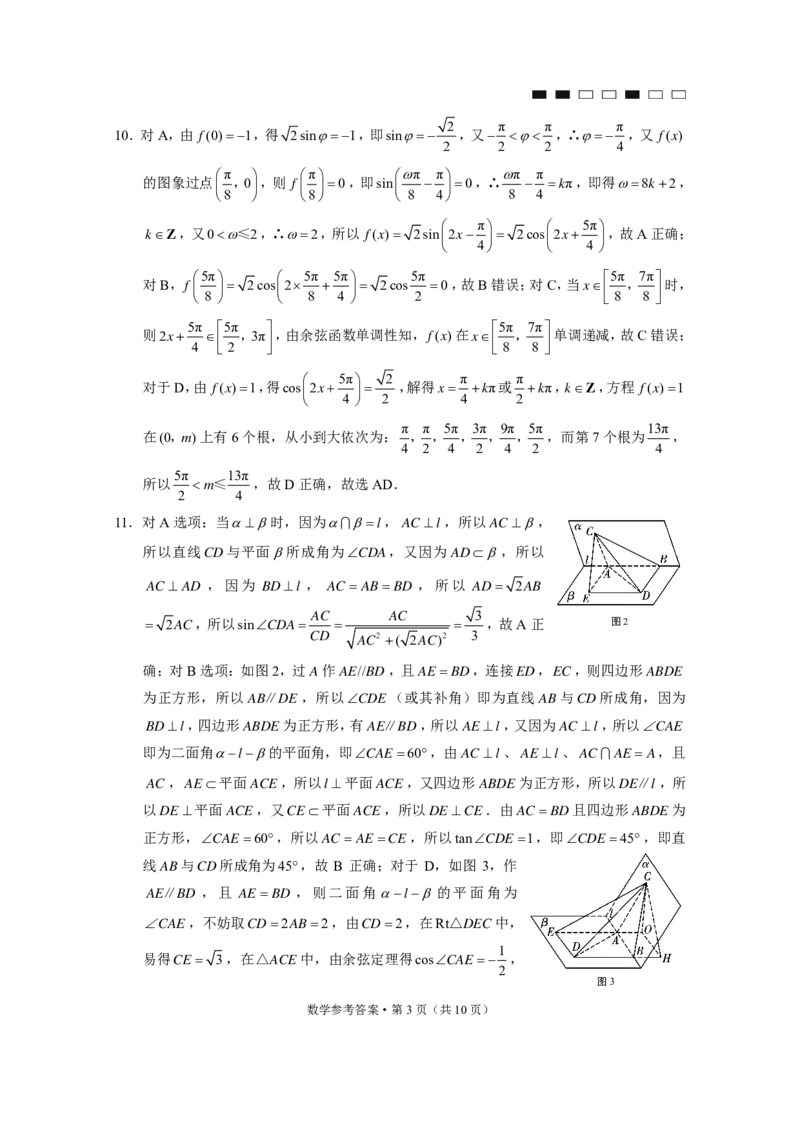11．对A选项：当时，因为l，AC l，所以AC ， 所以直线CD与平面所成角为CDA，又因为 AD，所以 AC AD ，因为 BDl ， AC  ABBD ，所以 AD 2AB AC AC 3  2AC，所以sinCDA   ，故A正 图2 CD AC2 ( 2AC)2 3 确；对B选项：如图2，过A作AE//BD，且AEBD，连接ED，EC，则四边形ABDE 为正方形，所以AB∥DE ，所以CDE（或其补角）即为直线AB与CD所成角，因为 BDl，四边形ABDE为正方形，有AE∥BD，所以AEl，又因为AC l，所以CAE 即为二面角l的平面角，即CAE60，由ACl、AEl、ACAE  A，且 AC，AE平面ACE，所以l平面ACE，又四边形ABDE为正方形，所以DE∥l ，所 以DE平面ACE，又CE平面ACE，所以DECE．由AC BD且四边形ABDE为 正方形，CAE60，所以AC AECE，所以tanCDE1，即CDE45，即直 线AB与CD所成角为45，故 B 正确；对于 D，如图 3，作 AE∥BD ，且 AEBD ，则二面角l的平面角为 CAE，不妨取CD2AB2，由CD2，在Rt△DEC中， 1 易得CE 3，在△ACE中，由余弦定理得cosCAE ， 2 图3 数学参考答案·第3页（共10页） {#{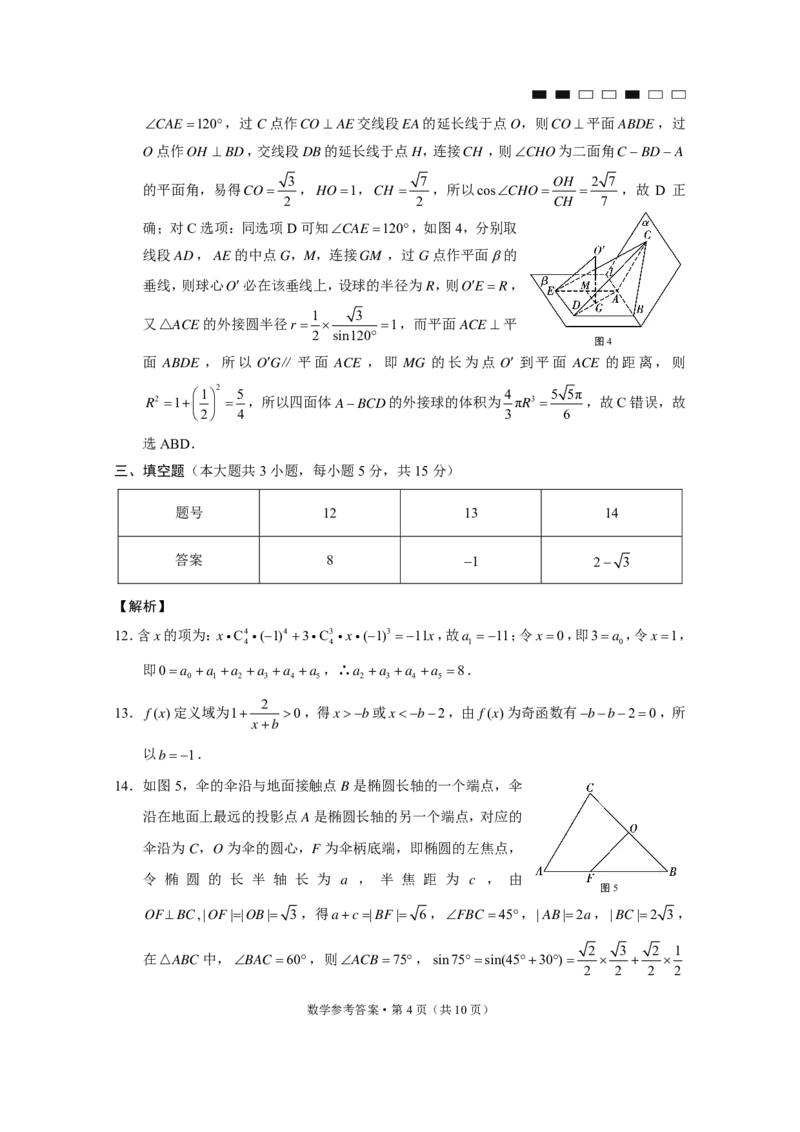QQABbQCEogCAQJIAARhCAQmwCAKQkAGAAKoGhAAMIAAAyRFABAA=}#}CAE120，过C点作CO AE交线段EA的延长线于点O，则CO平面ABDE，过 O点作OH BD，交线段DB的延长线于点H，连接CH ，则CHO为二面角CBDA 3 7 OH 2 7 的平面角，易得CO ，HO1，CH  ，所以cosCHO  ，故 D 正 2 2 CH 7 确；对C选项：同选项D可知CAE120，如图4，分别取 线段AD，AE的中点G，M，连接GM ，过G点作平面的 垂线，则球心O必在该垂线上，设球的半径为R，则OER， 1 3 又△ACE的外接圆半径r  1，而平面ACE平 2 sin120 图4 面 ABDE ，所以 OG∥ 平面 ACE ，即 MG 的长为点 O 到平面 ACE 的距离，则 1 2 5 4 5 5π R2 1   ，所以四面体ABCD的外接球的体积为 πR3  ，故C错误，故 2 4 3 6 选ABD． 三、填空题（本大题共3小题，每小题5分，共15分） 题号 12 13 14 答案 8 1 2 3 【解析】 12．含x的项为：xC4 (1)4 3C3 x(1)3 11x，故a 11；令x0，即3a ，令x1， 4 4 1 0 即0a a a a a a ，∴a a a a 8． 0 1 2 3 4 5 2 3 4 5 2 13．f(x)定义域为1 0，得xb或xb2，由 f(x)为奇函数有bb20，所 xb 以b1． 14．如图5，伞的伞沿与地面接触点B是椭圆长轴的一个端点，伞 沿在地面上最远的投影点A是椭圆长轴的另一个端点，对应的 伞沿为 C，O 为伞的圆心，F 为伞柄底端，即椭圆的左焦点， 令 椭 圆 的 长 半 轴 长 为 a ， 半 焦 距 为 c ， 由 图5 OF⊥BC,|OF||OB| 3，得ac|BF| 6，FBC45，|AB|2a，|BC|2 3， 2 3 2 1 在△ABC中，BAC60，则ACB75，sin75sin(4530)    2 2 2 2 数学参考答案·第4页（共10页） {#{QQABbQCEogCAQJIAARhCAQmwCAKQkAGAAKoGhAAMIAAAyRFABAA=}#}6 2 2a 2 3 2 6 6 2  ，由正弦定理得，  ，解得a ，则c ，所以 4 sin75 sin60 2 2 c 该椭圆的离心率e 2 3． a 四、解答题（共77分．解答应写出文字说明，证明过程或演算步骤） 15．（本小题满分13分） 解：（1）圆C ：(x3)2  y2 1的圆心为C (3，0)，半径为1， 1 1 圆C ：(x3)2  y2 1的圆心为C (3，0)，半径为1， 2 2 设圆C的半径为r ， 若圆C与圆C 内切，与圆C 外切，则|CC |r1，|CC |r1， 1 2 1 2 ……………………………………………………………（2分） 可得|CC ||CC |2； 2 1 若圆C与圆C 内切，与圆C 外切，则|CC |r1，|CC |r1， 2 1 2 1 ……………………………………………………………（4分） 可得|CC ||CC |2； 1 2 综上所述：||CC ||CC ||2， 1 2 可知：圆心C的轨迹E是以C 、C 为焦点的双曲线，且a1，c3， 1 2 可得b2 c2 a2 8， y2 所以圆心C的轨迹E的方程为x2  1． ……………………………（6分） 8  y2 x2  1， （2）联立方程 8  x ym0， 消去y得7x2 2mxm2 80， ………………………………………（8分） 则4m2 28(m2 8)32(m2 7)0，可知直线与双曲线相交， ………………………………………………………（9分） 数学参考答案·第5页（共10页） {#{QQABbQCEogCAQJIAARhCAQmwCAKQkAGAAKoGhAAMIAAAyRFABAA=}#}如图6，设A(x，y )，B(x，y )，线段AB的中点为M(x，y )， 1 1 2 2 0 0 x x m 8m m 8m 可得x  1 2  ，y x m ，即M ，  ， 0 2 7 0 0 7  7 7  ………………………………………………………（11分） m 8m 且M ，  在圆x2  y2 65上，  7 7  图6 m 2 8m 2 则     65，解得m7，  7   7  又m0，所以实数m的值为7． ………………………………………（13分） 16．（本小题满分15分） a 1 解：（1）函数 f(x)的定义域为{x|x0}， f(x)  2， x x2 ……………………………………………………（1分） 1 又曲线y f(x)在点(1，f(1))处的切线与直线y x垂直， 2 所以 f(1)a122，即a1． ………………………………………（3分） 1 (x1)(2x1) ∴f(x)lnx 2x， f(x) (x0)， x x2 1  1 由 f(x)0且x0，得0x ，即 f(x)的单调递减区间是 0，  ， 2  2 1 1  由 f(x)0得x ，即 f(x)的单调递增区间是  ， ． 2 2  ………………………………………………………（6分） m （2）由（1）知不等式 f(x)≥2x 恒成立， 2x 1 m m 可化为lnx 2x≥2x 恒成立，即 ≤xlnx1恒成立． x 2x 2 ………………………………………………………（8分） 令g(x)xlnx1， ……………………………………（10分）  1  1 当x0，  时，g(x)0，g(x)在 0，  上单调递减；  e  e 1  1  当x ， 时，g(x)0，g(x)在  ， 上单调递增． e  e  ………………………………………………………（12分） 数学参考答案·第6页（共10页） {#{QQABbQCEogCAQJIAARhCAQmwCAKQkAGAAKoGhAAMIAAAyRFABAA=}#}1 1 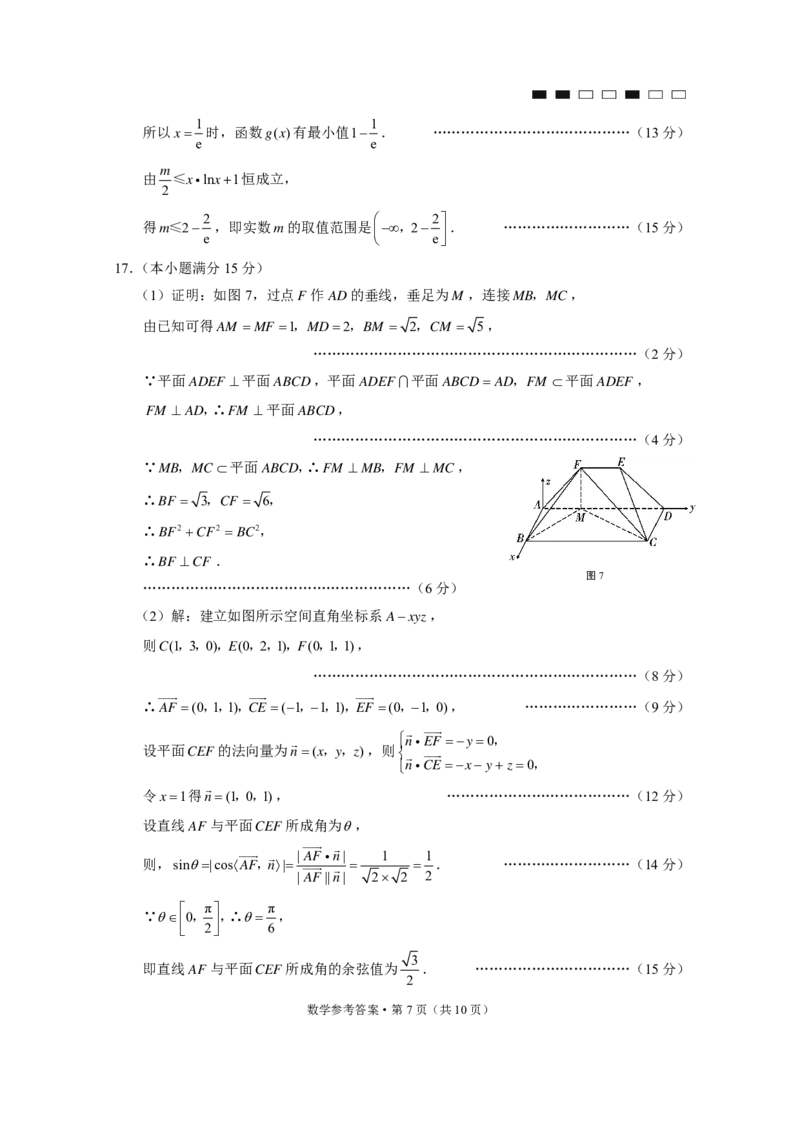所以x 时，函数g(x)有最小值1 ． ……………………………………（13分） e e m 由 ≤xlnx1恒成立， 2 2  2 得m≤2 ，即实数m的取值范围是 ，2  ． ………………………（15分） e  e 17．（本小题满分15分） （1）证明：如图7，过点F 作AD的垂线，垂足为M ，连接MB，MC， 由已知可得AM MF 1，MD2，BM  2，CM  5， ……………………………………………………………（2分） ∵平面ADEF 平面ABCD，平面ADEF平面ABCD AD，FM 平面ADEF， FM  AD，∴FM 平面ABCD， ……………………………………………………………（4分） ∵MB，MC平面ABCD，∴FM MB，FM MC， ∴BF  3，CF  6， ∴BF2 CF2 BC2， ∴BF CF ． 图7 …………………………………………………（6分） （2）解：建立如图所示空间直角坐标系Axyz， 则C(1，3，0)，E(0，2，1)，F(0，1，1)， ……………………………………………………………（8分）    ∴AF (0，1，1)，CE(1，1，1)，EF (0，1，0)， ……………………（9分）    nEF y0， 设平面CEF的法向量为n(x，y，z)，则  nCE x yz0，  令x1得n(1，0，1)， …………………………………（12分） 设直线AF 与平面CEF所成角为，     |AF n| 1 1 则，sin|cosAF，n|     ． ………………………（14分） |AF||n| 2 2 2  π π ∵ 0， ，∴ ，    2 6 3 即直线AF 与平面CEF所成角的余弦值为 ． ……………………………（15分） 2 数学参考答案·第7页（共10页） {#{QQABbQCEogCAQJIAARhCAQmwCAKQkAGAAKoGhAAMIAAAyRFABAA=}#}18．（本小题满分17分） C2C0 1 解：（1）由题可知2号盒子里有3个黑球的概率为P 2 2  ． C2 6 4 …………………………………………………………（3分） （2）由题可知可取1，2，3， C2 C2 C1C1 C2 7 P(1) 2  3  2 2  2  ， ………………………………………（4分） C2 C2 C2 C2 36 4 4 4 4 C2 C2 C1C1 C2 7 P(3) 2  3  2 2  2  ， ………………………………………（5分） C2 C2 C2 C2 36 4 4 4 4 11 P(2)1P(1)P(3) ， ………………………………………（6分） 18 所以3号盒子里的黑球的个数ξ的分布列为  1 2 3 7 11 7 P 36 18 36 ………………………………………（8分） 1 （3）记a 为第n(n≥2)号盒子有一个黑球和三个白球的概率，则a  ， n1 1 6 ……………………………………………………………（9分） 2 11 b 为第n(n≥2)号盒子有两个黑球和两个白球的概率，则b  ，b  ， n1 1 3 2 18 …………………………………………………………（10分） 则第n(n≥2)号盒子有三个黑球和一个白球的概率为1a b ， n1 n1 2 1 1 且b  b  a  (1a b )(n≥3)， n1 3 n2 2 n2 2 n2 n2 1 1 化解得b  b  ， ………………………………………（12分） n1 6 n2 2 3 1 3 3 1 得b   b   ，b   ， n1 5 6 n2 5 1 5 15 3 1 3  3 3 1 1 而b   b   ，则数列b  为等比数列，首项为b   ，公比为 ， 2 5 6 1 5  n 5 1 5 15 6 数学参考答案·第8页（共10页） {#{QQABbQCEogCAQJIAARhCAQmwCAKQkAGAAKoGhAAMIAAAyRFABAA=}#}3 1 1 n1 所以b     ， n 5 156 1 1 1 11 n 又由a  b  a 求得：a     ． ………………………（15分） n1 6 n2 2 n2 n 5 56 因此E(X )1a 2b 3(1a b )32a b 2． n n1 n1 n1 n1 n1 n1 ………………………………………（17分） 19．（本小题满分17分） （1）①解：因为A(0，2，1)，B(1，3，2)，    i j k            则OAOB 0 2 1 4i j02k03ii j2k (1，1，2)． 1 3 2 ……………………………………………………………（3分） ②证明：设A(x，y，z )，B(x，y，z )， 1 1 1 2 2 2         则OAOB y z i z x j x y k x yk z x j  y zi 1 2 1 2 1 2 2 1 2 1 2 1 (y z  y z，z x z x，x y x y )， 1 2 2 1 1 2 2 1 1 2 2 1 将x 与x 互换，y 与y 互换，z 与z 互换， 2 1 2 1 2 1   可得OBOA(y z  y z，z x z x，x y x y )， 2 1 1 2 2 1 1 2 2 1 1 2      故OAOBOBOA(0，0，0)0． ………………………………………（7分）   (OAOB)2 （2）证明：因为sinAOB 1cos2AOB  1   |OA|2|OB|2     |OA|2|OB|2 (OAOB)2    ， |OA||OB| 1   1     故S  |OA||OB|sinAOB |OA|2|OB|2 (OAOB)2 ， △AOB 2 2 1   故要证S  |OAOB|， △AOB 2       只需证|OAOB| |OA|2|OB|2 (OAOB)2 ，       即证|OAOB|2|OA|2|OB|2 (OAOB)2． 数学参考答案·第9页（共10页） {#{QQABbQCEogCAQJIAARhCAQmwCAKQkAGAAKoGhAAMIAAAyRFABAA=}#}    由（1）OA(x，y，z )，OB(x，y，z )，OAOB(y z  y z，z x z x，x y x y )， 1 1 1 2 2 2 1 2 2 1 1 2 2 1 1 2 2 1   故|OAOB|2(y z  y z )2 (z x z x )2 (x y x y )2， 1 2 2 1 1 2 2 1 1 2 2 1     又|OA|2x2  y2 z2，|OB|2x2  y2 z2，(OAOB)2 (xx  y y z z )2， 1 1 1 2 2 2 1 2 1 2 1 2       则|OAOB|2|OA|2|OB|2 (OAOB)2成立， 1   故S  |OAOB|． ………………………………………（13分） △AOB 2 1   （3）解：由（2）S  |OAOB|， △AOB 2     得(OAOB)2 |OAOB|2 1        |OAOB|2|OAOB|S 2|OAOB|， 2 △AOB   1   故(OAOB)2  S |OAOB|6， 3 △AOB     故(OAOB)2的几何意义表示以△AOB为底面、|OAOB|为高的三棱锥体积的6倍． ………………………………………（17分） 数学参考答案·第10页（共10页） {#{QQABbQCEogCAQJIAARhCAQmwCAKQkAGAAKoGhAAMIAAAyRFABAA=}#}