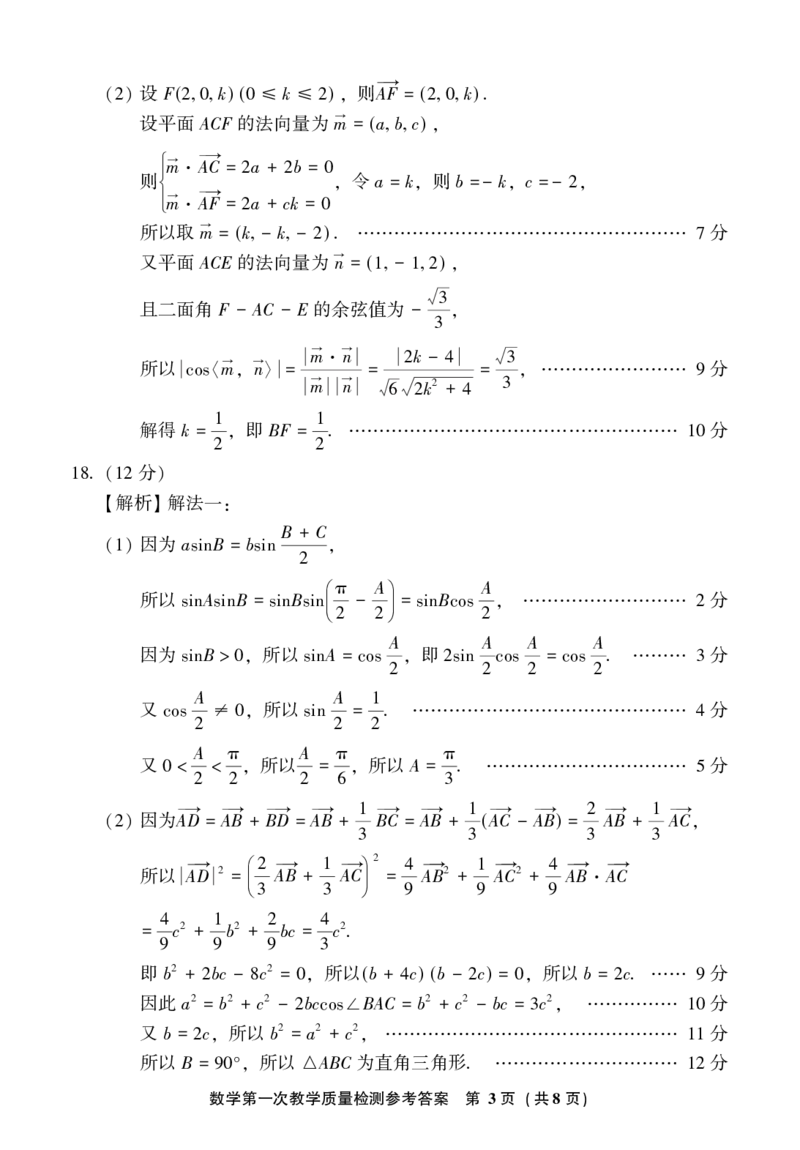福建省漳州市2023-2024学年高三上学期第一次教学质量检测数学试题(1)_2023年9月_029月合集_2024届福建省漳州市高三上学期第一次教学质量检测

准考证号 姓名 (在此卷上答题无效) 福建省漳州市 届高三毕业班第一次教学质量检测 ２０２４ 数 学 试 题 本试卷共 页 小题 满分 分 考试时间 分钟 ６ ꎬ ２２ ꎬ １５０ ꎬ １２０ ꎮ 考生注意: 答题前ꎬ 考生务必在试题卷、 答题卡规定的地方填写自己的准考证号、 姓名ꎮ 考生要 １􀆰 认真核对答题卡上粘贴的条形码的 “准考证号、 姓名” 与考生本人准考证号、 姓名是否一致ꎮ 回答选择题时ꎬ 选出每小题答案后ꎬ 用 铅笔把答题卡上对应题目的答案标号涂黑ꎮ ２􀆰 ２Ｂ 如需改动ꎬ 用橡皮擦干净后ꎬ 再选涂其它答案标号ꎮ 回答非选择题时ꎬ 用 黑色签字笔 ０􀆰５ｍｍ 将答案写在答题卡上ꎮ 写在本试卷上无效ꎮ 考试结束ꎬ 考生必须将试题卷和答题卡一并交回ꎮ ３􀆰 一、 单项选择题 (本大题共 小题ꎬ 每小题 分ꎬ 共 分ꎬ 在每小题给出的四个 ８ ５ ４０ 选项中ꎬ 只有一项是符合题目要求的) . 设全集 Ｕ ＝ Ｒ 若集合Ａ ＝{ｘ ｜ ｘ } Ｂ ＝{ ｘ ｜ ｙ ＝ ｘ － } 则如图所示 １ ꎬ １ ≤２ ≤４ ꎬ １ ꎬ 的阴影部分表示的集合为 (－ ) [ ] Ａ. ∞􀆯０ Ｂ. １􀆯２ ( ＋ ) (－ ) ( ＋ ) Ｃ. ２􀆯 ∞ Ｄ. ∞􀆯０ ∪ ２􀆯 ∞ . 已知复数 ｚ 满足 ｚ ＋ (ｚ － ) ＝ 为虚数单位 则 ｜ ｚ ｜ ＝ ２ １ ｉ ３(ｉ )ꎬ Ａ. １ Ｂ. ３ Ｃ. ２ Ｄ. ５ . 已知函数 ｆ (ｘ) ＝ ｘ ＋ ｘ ｇ(ｘ) ＝ ｘ ＋ ｘ ｈ(ｘ) ＝ ｘ３ ＋ ｘ 的零点分别是 ａ ｂ ｃ 则 ３ ２ 􀆯 ｌｏｇ２ 􀆯 􀆯 􀆯 ꎬ ａ ｂ ｃ 的大小关系是 􀆯 􀆯 ａ>ｂ>ｃ ｂ>ｃ>ａ ｃ>ａ>ｂ ｂ>ａ>ｃ Ａ. Ｂ. Ｃ. Ｄ. . 已知向量 →ａ ＝ (－ ) →ｂ ＝ ( ｘ) 若 →ａ →ｂ 则 →ａ － →ｂ ＝ ４ １􀆯１ 􀆯 ２􀆯 ꎬ ⊥ ꎬ Ａ. ２ Ｂ. ２ ２ Ｃ. １０ Ｄ. ２ ３ ｘ２ ｙ２ . 已知双曲线 － ＝ (ａ> ｂ> ) 的一条渐近线被圆(ｘ － ) ２ ＋ ｙ２ ＝ 所截得的弦 ５ ａ２ ｂ２ １ ０􀆯 ０ ２ ４ 长为 则双曲线的离心率为 ２ꎬ Ａ. ３ Ｂ. ２ Ｃ. ５ Ｄ. １０ 数学第一次教学质量检测 第 １页 (共６页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}æ ö . 已知 çα － π÷ ＝ １ 则 α ＝ ６ ｓｉｎè ø ꎬ ｓｉｎ２ ４ ３ － ７ － ４ ２ ４ ２ ７ Ａ. Ｂ. Ｃ. Ｄ. ９ ９ ９ ９ . 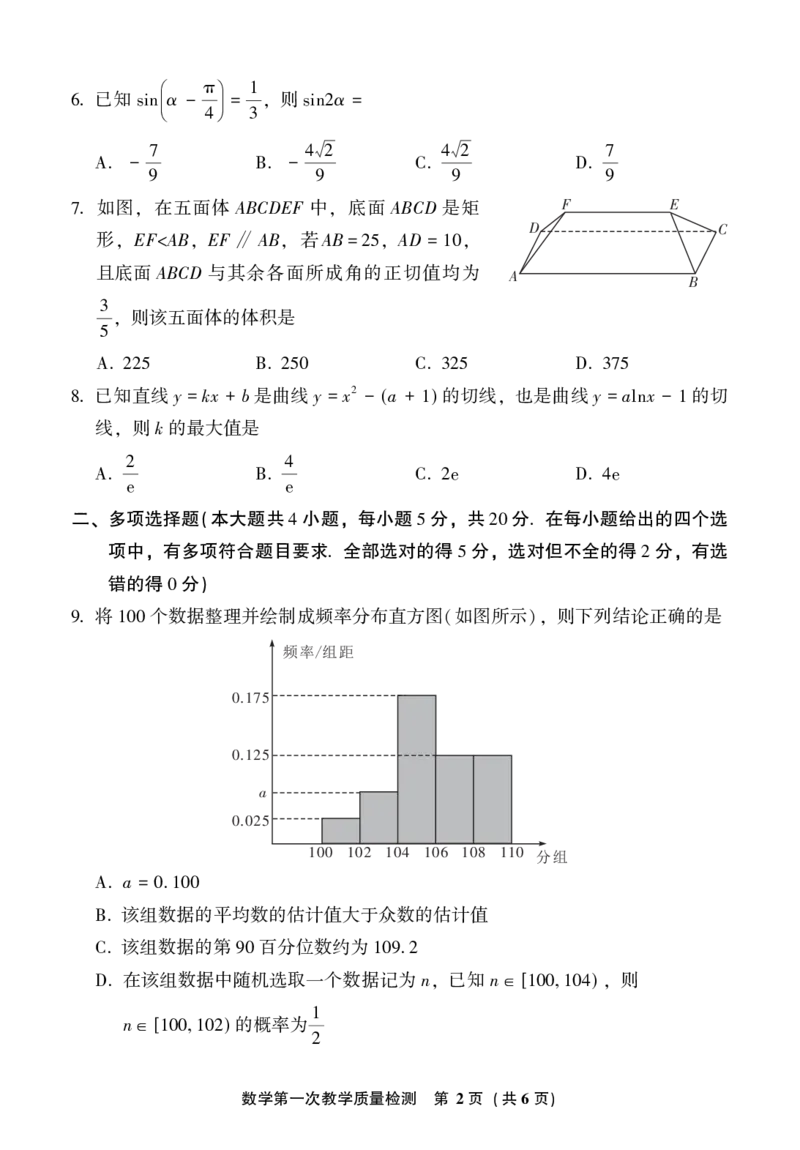如图 在五面体 ＡＢＣＤＥＦ 中 底面 ＡＢＣＤ 是矩 F E ７ ꎬ ꎬ D C 形 ＥＦ<ＡＢ ＥＦ ＡＢ 若ＡＢ ＝ ＡＤ ＝ ꎬ ꎬ ∥ ꎬ ２５ꎬ １０ꎬ 且底面 ＡＢＣＤ 与其余各面所成角的正切值均为 A B ３ 则该五面体的体积是 ꎬ ５ Ａ. ２２５ Ｂ. ２５０ Ｃ. ３２５ Ｄ. ３７５ . 已知直线 ｙ ＝ ｋｘ ＋ ｂ 是曲线 ｙ ＝ ｘ２ － (ａ ＋ ) 的切线 也是曲线 ｙ ＝ ａ ｘ － 的切 ８ １ ꎬ ｌｎ １ 线 则 ｋ 的最大值是 ꎬ ２ ４ Ａ. Ｂ. Ｃ. ２ｅ Ｄ. ４ｅ ｅ ｅ 二、 多项选择题(本大题共 小题ꎬ 每小题 分ꎬ 共 分. 在每小题给出的四个选 ４ ５ ２０ 项中ꎬ 有多项符合题目要求. 全部选对的得 分ꎬ 选对但不全的得 分ꎬ 有选 ５ ２ 错的得 分) ０ . 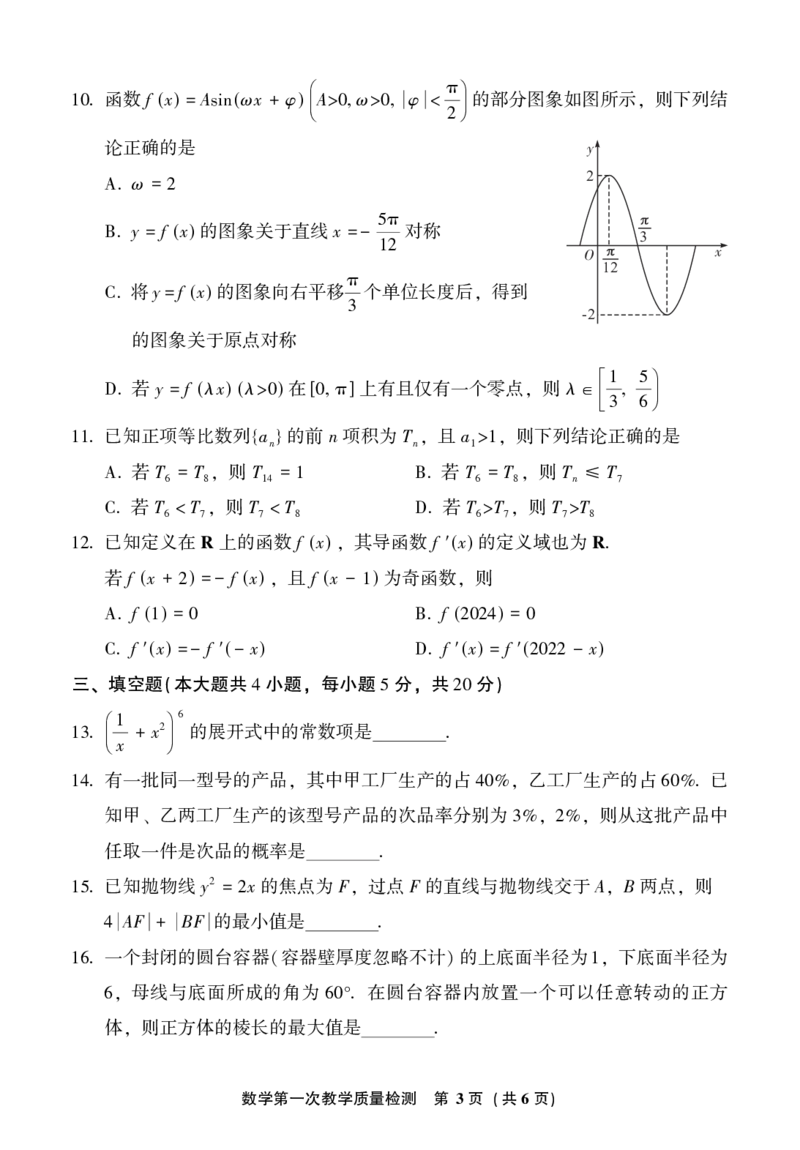将 个数据整理并绘制成频率分布直方图 如图所示 则下列结论正确的是 ９ １００ ( )ꎬ #$/"% 0.175 0.125 a 0.025 100 102 104 106 108 110 !" ａ ＝ Ａ. ０􀆰１００ 该组数据的平均数的估计值大于众数的估计值 Ｂ. 该组数据的第 百分位数约为 Ｃ. ９０ １０９􀆰２ 在该组数据中随机选取一个数据记为 ｎ 已知 ｎ [ ) 则 Ｄ. ꎬ ∈ １００􀆯１０４ ꎬ ｎ [ ) 的概率为１ ∈ １００􀆯１０２ ２ 数学第一次教学质量检测 第 ２页 (共６页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}æ ö . 函数ｆ (ｘ) ＝Ａ (ωｘ ＋ φ) çＡ> ω> φ < π÷ 的部分图象如图所示 则下列结 １０ ｓｉｎ è ０􀆯 ０􀆯 ø ꎬ ２ 论正确的是 y 2 ω ＝ Ａ. ２ ｙ ＝ ｆ (ｘ) 的图象关于直线 ｘ ＝－ ５π 对称 3 Ｂ. １２ O x 12 将ｙ ＝ｆ (ｘ) 的图象向右平移π 个单位长度后 得到 Ｃ. ꎬ ３ -2 的图象关于原点对称 é ö 若 ｙ ＝ ｆ (λｘ) (λ> ) 在[ ] 上有且仅有一个零点 则 λ ê １ ５ ÷ ê Ｄ. ０ ０􀆯 π ꎬ ∈ë 􀆯 ø ３ ６ . 已知正项等比数列{ａ }的前 ｎ 项积为 Ｔ 且 ａ > 则下列结论正确的是 １１ ｎ ｎꎬ １ １ꎬ 若 Ｔ ＝ Ｔ 则 Ｔ ＝ 若 Ｔ ＝ Ｔ 则 Ｔ Ｔ Ａ. ６ ８ꎬ １４ １ Ｂ. ６ ８ꎬ ｎ ≤ ７ 若 Ｔ <Ｔ 则 Ｔ <Ｔ 若 Ｔ >Ｔ 则 Ｔ >Ｔ Ｃ. ６ ７ꎬ ７ ８ Ｄ. ６ ７ꎬ ７ ８ . 已知定义在 Ｒ 上的函数 ｆ (ｘ) 其导函数 ｆ ′(ｘ) 的定义域也为 Ｒ. １２ ꎬ 若 ｆ (ｘ ＋ ) ＝－ ｆ (ｘ) 且 ｆ (ｘ － ) 为奇函数 则 ２ ꎬ １ ꎬ ｆ ( ) ＝ ｆ ( ) ＝ Ａ. １ ０ Ｂ. ２０２４ ０ ｆ ′(ｘ) ＝－ ｆ ′(－ ｘ) ｆ ′(ｘ) ＝ ｆ ′( － ｘ) Ｃ. Ｄ. ２０２２ 三、 填空题(本大题共 小题ꎬ 每小题 分ꎬ 共 分) ４ ５ ２０ æ ö ６ . ç１ ＋ ｘ２÷ 的展开式中的常数项是 . １３ è ｘ ø . 有一批同一型号的产品 其中甲工厂生产的占 ％ 乙工厂生产的占 ％. 已 １４ ꎬ ４０ ꎬ ６０ 知甲 乙两工厂生产的该型号产品的次品率分别为 ％ ％ 则从这批产品中 、 ３ ꎬ ２ ꎬ 任取一件是次品的概率是 . . 已知抛物线 ｙ２ ＝ ｘ 的焦点为 Ｆ 过点 Ｆ 的直线与抛物线交于 Ａ Ｂ 两点 则 １５ ２ ꎬ ꎬ ꎬ ＡＦ ＋ ＢＦ 的最小值是 . ４ . 一个封闭的圆台容器 容器壁厚度忽略不计 的上底面半径为 下底面半径为 １６ ( ) １ꎬ 母线与底面所成的角为 °. 在圆台容器内放置一个可以任意转动的正方 ６ꎬ ６０ 体 则正方体的棱长的最大值是 . ꎬ 数学第一次教学质量检测 第 ３页 (共６页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}四、 解答题(本大题共 小题ꎬ 共 分ꎬ 解答应写出文字说明ꎬ 证明过程或演算步 ６ ７０ 骤) . 本小题满分 分 １７ ( １０ ) 如图 正方体 ＡＢＣＤ － Ａ Ｂ Ｃ Ｄ 的棱长为 Ｅ 为棱 ＤＤ 的中点. ꎬ １ １ １ １ ２ꎬ １ 证明 ＢＤ 平面 ＡＣＥ (１) : １ ∥ ꎻ 若 Ｆ 是棱 ＢＢ 上一点 且二面角 Ｆ － ＡＣ － Ｅ 的余弦值为 － ３ 求 ＢＦ. (２) １ ꎬ ꎬ ３ . 本小题满分 分 １８ ( １２ ) Ｂ ＋ Ｃ 已知 ＡＢＣ 的内角 Ａ Ｂ Ｃ 的对边分别为 ａ ｂ ｃ 且 ａ Ｂ ＝ ｂ . △ ꎬ ꎬ ꎬ ꎬ ꎬ ｓｉｎ ｓｉｎ ２ 求 Ａ (１) ꎻ 若Ｄ为边ＢＣ上一点 且ＢＤ ＝ １ＢＣ ＡＤ ＝ ２ ３ｃ 证明 ＡＢＣ为直角三 (２) ꎬ ꎬ ꎬ : △ ３ ３ 角形. . 本小题满分 分 １９ ( １２ ) ａ 已知数列{ａ } {ｂ }满足ａ ＝ ｂ ＝ ｂ ＝ ｎ ｂ 记Ｔ 为{ｂ }的前ｎ项和. ｎ ꎬ ｎ １ １ １ꎬ ｎ＋ １ ａ ｎꎬ ｎ ｎ ｎ＋ ２ 若{ａ }为等比数列 其公比 ｑ ＝ 求 Ｔ (１) ｎ ꎬ ２ꎬ ｎꎻ 若{ａ }为等差数列 其公差 ｄ ＝ 证明 Ｔ < ３. (２) ｎ ꎬ ２ꎬ : ｎ ２ 数学第一次教学质量检测 第 ４页 (共６页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}. 本小题满分 分 ２０ ( １２ ) 甲 乙两选手进行一场体育竞技比赛 采用 ｎ － (ｎ Ｎ ∗ ) 局 ｎ 胜制 当一选 、 ꎬ ２ １ ∈ ( 手先赢下ｎ局比赛时 该选手获胜 比赛结束 . 已知每局比赛甲获胜的概率为ｐ ꎬ ꎬ ) ꎬ 乙获胜的概率为 － ｐ. １ 若 ｎ ＝ ｐ ＝ １ 比赛结束时的局数为 Ｘ 求 Ｘ 的分布列与数学期望 (１) ２ꎬ ꎬ ꎬ ꎻ ２ 若 ｎ ＝ 比 ｎ ＝ 对甲更有利 求 ｐ 的取值范围. (２) ３ ２ ꎬ . 本小题满分 分 ２１ ( １２ ) 已知椭圆 Ｃ ｘ２ ＋ ｙ２ ＝ (ａ >ｂ > ) 的左焦点为 Ｆ ( － ) 且过点 : ａ２ ｂ２ １ ０ １ ３􀆯０ ꎬ æ ö Ａç １ ÷ . è ３􀆯 ø ２ 求 Ｃ 的方程 (１) ꎻ 不过原点Ｏ的直线ｌ与Ｃ交于Ｐ Ｑ两点 且直线ＯＰ ＰＱ ＯＱ的斜率成 (２) ꎬ ꎬ ꎬ ꎬ 等比数列. 求 ｌ 的斜率 (ⅰ) ꎻ 求 ＯＰＱ 的面积的取值范围. (ⅱ) △ 数学第一次教学质量检测 第 ５页 (共６页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}. 本小题满分 分 ２２ ( １２ ) 已知函数 ｆ (ｘ) ＝ ａ ｘ ＋ ｘ ＋ . ｅ １ 讨论 ｆ (ｘ) 的单调性 (１) ꎻ ｘ － 当 ｘ> 时 ｆ (ｘ)> １ ＋ ｘ 求实数 ａ 的取值范围. (２) １ ꎬ ｌｎ ａ ꎬ 数学第一次教学质量检测 第 ６页 (共６页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}福建省漳州市 届高三毕业班第一次教学质量检测 ２０２４ 数学参考答案及评分细则 评分说明: 本解答给出了一种或几种解法供参考ꎬ 如果考生的解法与本解答不同ꎬ 可根据试题的 １. 主要考查内容比照评分标准制定相应的评分细则ꎮ 对计算题ꎬ 当考生的解答在某一步出现错误时ꎬ 如果后继部分的解答未改变该题的内 ２. 容和难度ꎬ 可视影响的程度决定后继部分的给分ꎬ 但不得超过该部分正确解答应给分数的一 半ꎻ 如果后继部分的解答有较严重的错误ꎬ 就不再给分ꎮ 解答右端所注分数ꎬ 表示考生正确做到这一步应得的累加分数ꎮ ３. 只给整数分数ꎮ 选择题和填空题不给中间分ꎮ ４. 一、 单项选择题: 本大题共 小题ꎬ 每小题 分ꎬ 共 分ꎬ 在每小题给出的四个 ８ ５ ４０ 选项中ꎬ 只有一项是符合题目要求的ꎮ １ ２ ３ ４ ５ ６ ７ ８ Ａ Ｄ Ｂ Ｃ Ｂ Ｄ Ｃ Ｂ 二、 多项选择题: 本大题共 小题ꎬ 每小题 分ꎬ 共 分ꎬ 在每小题给出的四个 ４ ５ ２０ 选项中ꎬ 有多个选项符合题目要求ꎬ 全部选对的得 分ꎬ 选对但不全的得 ５ ２ 分ꎬ 有选错的得 分ꎮ ０ ９ １０ １１ １２ ＢＣ ＡＢＤ ＡＢＤ ＡＣＤ 三、 填空题: 本题共 小题ꎬ 每小题 分ꎬ 共 分ꎮ ４ ５ ２０ ９ １３. １５ １４. ０􀆰０２４ １５. １６. ４ ２ 四、 解答题: 本大题共 小题ꎬ 共 分ꎬ 解答应写出文字说明ꎬ 证明过程或演算 ６ ７０ 步骤ꎮ . 分 １７ (１０ ) 解析 解法一 【 】 : 证明 连接 ＢＤ 交 ＡＣ 于点 Ｇ 连接 ＥＧ 分 (１) : ꎬ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １ 则 Ｇ 为 ＤＢ 中点 又 Ｅ 为 ＤＤ 中点 所以 ＧＥ ＢＤ 分 ꎬ １ ꎬ ∥ １ꎬ 􀆺􀆺􀆺􀆺􀆺 ２ 又 ＢＤ 平面 ＡＣＥ ＧＥ 平面 ＡＣＥ 所以 ＢＤ 平面 ＡＣＥ. 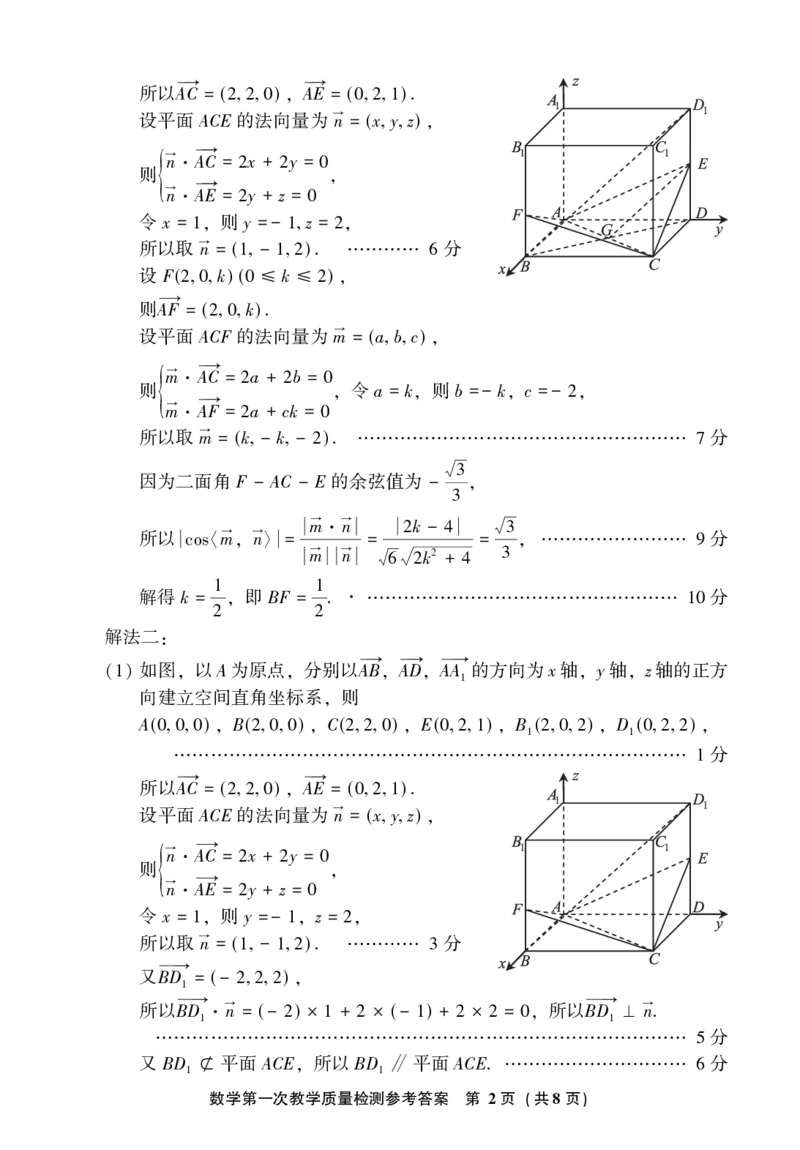分 １⊄ 􀆯 ⊂ ꎬ １ ∥ 􀆺􀆺􀆺 ４ 如图 以Ａ为原点 分别以Ａ→Ｂ Ａ→Ｄ ＡＡ→的方向为ｘ轴 ｙ轴 ｚ轴的正方向 (２) ꎬ ꎬ 􀆯 􀆯 １ ꎬ ꎬ 建立空间直角坐标系 则 Ａ( ) Ｂ( ) Ｃ( ) Ｅ( ) ꎬ ０􀆯０􀆯０ ꎬ ２􀆯０􀆯０ ꎬ ２􀆯２􀆯０ ꎬ ０􀆯２􀆯１ ꎬ Ｂ ( ) 分 １ ２􀆯０􀆯２ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ 数学第一次教学质量检测参考答案 第 １页 (共８页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}所以Ａ→Ｃ ＝ ( ) Ａ→Ｅ ＝ ( ) . ２􀆯２􀆯０ ꎬ ０􀆯２􀆯１ 设平面 ＡＣＥ 的法向量为 →ｎ ＝ (ｘ ｙ ｚ) 􀆯 􀆯 ꎬ { →ｎ Ａ→Ｃ ＝ ｘ ＋ ｙ ＝ 则 􀅰 ２ ２ ０ ꎬ →ｎ Ａ→Ｅ ＝ ｙ ＋ ｚ ＝ 􀅰 ２ ０ 令 ｘ ＝ 则 ｙ ＝－ ｚ ＝ １ꎬ １􀆯 ２ꎬ 所以取 →ｎ ＝ ( － ) . 分 １􀆯 １􀆯２ 􀆺􀆺􀆺􀆺 ６ 设 Ｆ( ｋ) ( ｋ ) ２􀆯０􀆯 ０ ≤ ≤２ ꎬ 则Ａ→Ｆ ＝ ( ｋ) . ２􀆯０􀆯 设平面 ＡＣＦ 的法向量为 ｍ→ ＝ (ａ ｂ ｃ) 􀆯 􀆯 ꎬ { ｍ→ Ａ→Ｃ ＝ ａ ＋ ｂ ＝ 则 􀅰 ２ ２ ０ 令 ａ ＝ ｋ 则 ｂ ＝－ ｋ ｃ ＝－ ꎬ ꎬ ꎬ ２ꎬ ｍ→ Ａ→Ｆ ＝ ａ ＋ ｃｋ ＝ 􀅰 ２ ０ 所以取 ｍ→ ＝ (ｋ － ｋ － ) . 分 􀆯 􀆯 ２ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ 因为二面角 Ｆ － ＡＣ － Ｅ 的余弦值为 － ３ ꎬ ３ ｍ→ →ｎ ｋ － 所以 ｍ→ →ｎ ＝ 􀅰 ＝ ２ ４ ＝ ３ 分 ｃｏｓ‹ ꎬ › ｍ→ →ｎ ｋ２ ＋ ３ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ９ ６ ２ ４ 解得 ｋ ＝ １ 即 ＢＦ ＝ １. 分 ꎬ ∙ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １０ ２ ２ 解法二 : 如图 以Ａ为原点 分别以Ａ→Ｂ Ａ→Ｄ ＡＡ→的方向为ｘ轴 ｙ轴 ｚ轴的正方 (１) ꎬ ꎬ ꎬ ꎬ １ ꎬ ꎬ 向建立空间直角坐标系 则 ꎬ Ａ( ) Ｂ( ) Ｃ( ) Ｅ( ) Ｂ ( ) Ｄ ( ) ０􀆯０􀆯０ ꎬ ２􀆯０􀆯０ ꎬ ２􀆯２􀆯０ ꎬ ０􀆯２􀆯１ ꎬ １ ２􀆯０􀆯２ ꎬ １ ０􀆯２􀆯２ ꎬ 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １ 所以Ａ→Ｃ ＝ ( ) Ａ→Ｅ ＝ ( ) . ２􀆯２􀆯０ ꎬ ０􀆯２􀆯１ 设平面 ＡＣＥ 的法向量为 →ｎ ＝ (ｘ ｙ ｚ) 􀆯 􀆯 ꎬ { →ｎ Ａ→Ｃ ＝ ｘ ＋ ｙ ＝ 则 􀅰 ２ ２ ０ ꎬ →ｎ Ａ→Ｅ ＝ ｙ ＋ ｚ ＝ 􀅰 ２ ０ 令 ｘ ＝ 则 ｙ ＝－ ｚ ＝ １ꎬ １ꎬ ２ꎬ 所以取 →ｎ ＝ ( － ) . 分 １􀆯 １􀆯２ 􀆺􀆺􀆺􀆺 ３ 又ＢＤ→ ＝ (－ ) １ ２􀆯２􀆯２ ꎬ 所以ＢＤ→ →ｎ ＝ (－ ) × ＋ × (－ ) ＋ × ＝ 所以ＢＤ→ →ｎ. １􀅰 ２ １ ２ １ ２ ２ ０ꎬ １ ⊥ 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ 又 ＢＤ 平面 ＡＣＥ 所以 ＢＤ 平面 ＡＣＥ. 分 １ ⊄ ꎬ １ ∥ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ６ 数学第一次教学质量检测参考答案 第 ２页 (共８页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}设 Ｆ( ｋ) ( ｋ ) 则Ａ→Ｆ ＝ ( ｋ) . (２) ２􀆯０􀆯 ０ ≤ ≤２ ꎬ ２􀆯０􀆯 设平面 ＡＣＦ 的法向量为 ｍ→ ＝ (ａ ｂ ｃ) 􀆯 􀆯 ꎬ ì ïïｍ→ Ａ→Ｃ ＝ ａ ＋ ｂ ＝ 则í 􀅰 ２ ２ ０ 令 ａ ＝ ｋ 则 ｂ ＝－ ｋ ｃ ＝－ ïï ꎬ ꎬ ꎬ ２ꎬ îｍ→ Ａ→Ｆ ＝ ａ ＋ ｃｋ ＝ 􀅰 ２ ０ 所以取 ｍ→ ＝ (ｋ － ｋ － ) . 分 􀆯 􀆯 ２ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ 又平面 ＡＣＥ 的法向量为 →ｎ ＝ ( － ) １􀆯 １􀆯２ ꎬ 且二面角 Ｆ － ＡＣ － Ｅ 的余弦值为 － ３ ꎬ ３ ｍ→ →ｎ ｋ － 所以 ｍ→ →ｎ ＝ 􀅰 ＝ ２ ４ ＝ ３ 分 ｃｏｓ‹ ꎬ › ｍ→ →ｎ ｋ２ ＋ ３ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ９ ６ ２ ４ 解得 ｋ ＝ １ 即 ＢＦ ＝ １. 分 ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １０ ２ ２ . 分 １８ (１２ ) 解析 解法一 【 】 : Ｂ ＋ Ｃ 因为 ａ Ｂ ＝ ｂ (１) ｓｉｎ ｓｉｎ ꎬ ２ æ Ａö Ａ 所以 Ａ Ｂ ＝ Ｂ çπ － ÷ ＝ Ｂ 分 ｓｉｎ ｓｉｎ ｓｉｎ ｓｉｎè ø ｓｉｎ ｃｏｓ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ２ ２ ２ ２ Ａ Ａ Ａ Ａ 因为 Ｂ > 所以 Ａ ＝ 即 ＝ . 分 ｓｉｎ ０ꎬ ｓｉｎ ｃｏｓ ꎬ ２ｓｉｎ ｃｏｓ ｃｏｓ 􀆺􀆺􀆺 ３ ２ ２ ２ ２ Ａ Ａ 又 所以 ＝ １. 分 ｃｏｓ ≠０ꎬ ｓｉｎ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ４ ２ ２ ２ Ａ Ａ 又 < < π 所以 ＝ π 所以 Ａ ＝ π. 分 ０ ꎬ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ ２ ２ ２ ６ ３ 因为Ａ→Ｄ ＝ Ａ→Ｂ ＋ Ｂ→Ｄ ＝ Ａ→Ｂ ＋ １ Ｂ→Ｃ ＝ Ａ→Ｂ ＋ １ (Ａ→Ｃ － Ａ→Ｂ) ＝ ２ Ａ→Ｂ ＋ １ Ａ→Ｃ (２) ꎬ ３ ３ ３ ３ æ ö ２ 所以 Ａ→Ｄ ２ ＝ ç ２ Ａ→Ｂ ＋ １ Ａ→Ｃ÷ ＝ ４ Ａ→Ｂ２ ＋ １ Ａ→Ｃ２ ＋ ４ Ａ→Ｂ Ａ→Ｃ è ø 􀅰 ３ ３ ９ ９ ９ ＝ ４ｃ２ ＋ １ｂ２ ＋ ２ｂｃ ＝ ４ｃ２. ９ ９ ９ ３ 即 ｂ２ ＋ ｂｃ － ｃ２ ＝ 所以(ｂ ＋ ｃ) (ｂ － ｃ) ＝ 所以 ｂ ＝ ｃ. 分 ２ ８ ０ꎬ ４ ２ ０ꎬ ２ 􀆺􀆺 ９ 因此 ａ２ ＝ ｂ２ ＋ ｃ２ － ｂｃ ＢＡＣ ＝ ｂ２ ＋ ｃ２ － ｂｃ ＝ ｃ２ 分 ２ ｃｏｓ∠ ３ ꎬ 􀆺􀆺􀆺􀆺􀆺 １０ 又 ｂ ＝ ｃ 所以 ｂ２ ＝ ａ２ ＋ ｃ２ 分 ２ ꎬ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １１ 所以 Ｂ ＝ ° 所以 ＡＢＣ 为直角三角形. 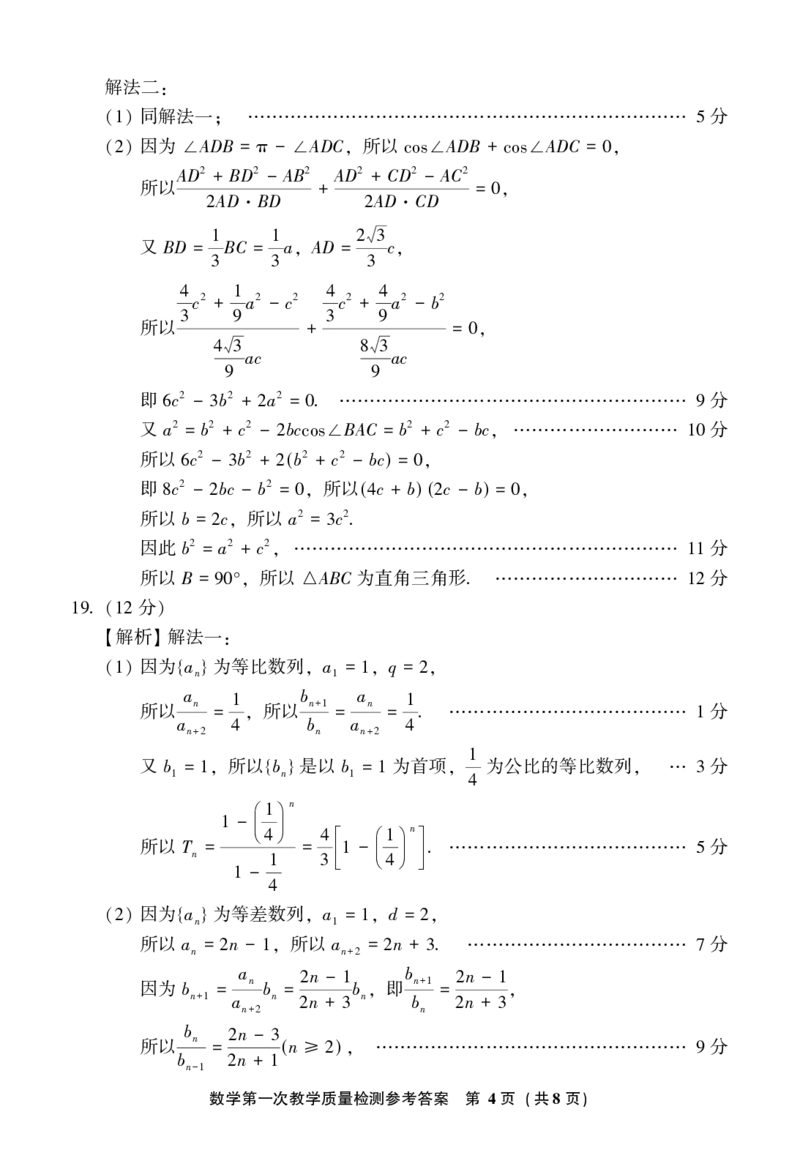分 ９０ ꎬ △ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ 数学第一次教学质量检测参考答案 第 ３页 (共８页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}解法二 : 同解法一 分 (１) ꎻ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ 因为 ＡＤＢ ＝ － ＡＤＣ 所以 ＡＤＢ ＋ ＡＤＣ ＝ (２) ∠ π ∠ ꎬ ｃｏｓ∠ ｃｏｓ∠ ０ꎬ ＡＤ２ ＋ ＢＤ２ － ＡＢ２ ＡＤ２ ＋ ＣＤ２ － ＡＣ２ 所以 ＋ ＝ ＡＤ ＢＤ ＡＤ ＣＤ ０ꎬ ２ 􀅰 ２ 􀅰 又 ＢＤ ＝ １ＢＣ ＝ １ａ ＡＤ ＝ ２ ３ｃ ꎬ ꎬ ３ ３ ３ ４ｃ２ ＋ １ａ２ － ｃ２ ４ｃ２ ＋ ４ａ２ － ｂ２ 所以３ ９ ＋ ３ ９ ＝ ０ꎬ ４ ３ａｃ ８ ３ａｃ ９ ９ 即 ｃ２ － ｂ２ ＋ ａ２ ＝ . 分 ６ ３ ２ ０ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ９ 又 ａ２ ＝ ｂ２ ＋ ｃ２ － ｂｃ ＢＡＣ ＝ ｂ２ ＋ ｃ２ － ｂｃ 分 ２ ｃｏｓ∠ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １０ 所以 ｃ２ － ｂ２ ＋ (ｂ２ ＋ ｃ２ － ｂｃ) ＝ ６ ３ ２ ０ꎬ 即 ｃ２ － ｂｃ － ｂ２ ＝ 所以( ｃ ＋ ｂ) ( ｃ － ｂ) ＝ ８ ２ ０ꎬ ４ ２ ０ꎬ 所以 ｂ ＝ ｃ 所以 ａ２ ＝ ｃ２. ２ ꎬ ３ 因此 ｂ２ ＝ ａ２ ＋ ｃ２ 分 ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １１ 所以 Ｂ ＝ ° 所以 ＡＢＣ 为直角三角形. 分 ９０ ꎬ △ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ . 分 １９ (１２ ) 解析 解法一 【 】 : 因为{ａ }为等比数列 ａ ＝ ｑ ＝ (１) ｎ ꎬ １ １ꎬ ２ꎬ ａ ｂ ａ ｎ ｎ＋ ｎ 所以 ＝ １ 所以 １ ＝ ＝ １. 分 ａ ꎬ ｂ ａ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １ ｎ＋ ２ ４ ｎ ｎ＋ ２ ４ 又 ｂ ＝ 所以{ｂ }是以 ｂ ＝ 为首项 １ 为公比的等比数列 分 １ １ꎬ ｎ １ １ ꎬ ꎬ 􀆺 ３ ４ æ ö ｎ － ç １÷ １ è ø é æ ö ｎù 所以 Ｔ ＝ ４ ＝ ４ ê － ç １÷ ú . 分 ｎ ë ê １ è ø û ú 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ － １ ３ ４ １ ４ 因为{ａ }为等差数列 ａ ＝ ｄ ＝ (２) ｎ ꎬ １ １ꎬ ２ꎬ 所以 ａ ＝ ｎ － 所以 ａ ＝ ｎ ＋ . 分 ｎ ２ １ꎬ ｎ＋ ２ ２ ３ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ ａ ｎ － ｂ ｎ － ｎ ｎ＋ 因为 ｂ ＝ ｂ ＝ ２ １ｂ 即 １ ＝ ２ １ ｎ＋ １ ａ ｎ ｎ ＋ ｎꎬ ｂ ｎ ＋ ꎬ ｎ＋ ２ ２ ３ ｎ ２ ３ ｂ ｎ － 所以 ｎ ＝ ２ ３(ｎ ) 分 ｂ ｎ ＋ ≥２ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ９ ｎ－ １ ２ １ 数学第一次教学质量检测参考答案 第 ４页 (共８页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}所以当 ｎ 时 ≥２ ꎬ ｂ ｂ ｂ ｂ ｂ ｎ ｎ－ ｎ－ ｂ ＝ × １ × ２ × × ３ × ２ × ｂ ｎ ｂ ｂ ｂ 􀆺 ｂ ｂ １ ｎ－ ｎ－ ｎ－ １ ２ ３ ２ １ ｎ － ｎ － ｎ － ＝ ２ ３ × ２ ５ × ２ ７ × × ３ × １ × ＝ ３ . ｎ ＋ ｎ － ｎ － 􀆺 １ ( ｎ － ) ( ｎ ＋ ) ２ １ ２ １ ２ ３ ７ ５ ２ １ ２ １ 又 ｂ ＝ 符合上式 １ １ ꎬ æ ö 所以 ｂ ＝ ３ ＝ ３ç １ － １ ÷ . 分 ｎ ( ｎ － ) ( ｎ ＋ ) è ｎ － ｎ ＋ ø 􀆺􀆺􀆺􀆺􀆺􀆺 １０ ２ １ ２ １ ２ ２ １ ２ １ 所以 Ｔ ＝ ｂ ＋ ｂ ＋ ｂ ＋ ＋ ｂ ＋ ｂ ｎ １ ２ ３ 􀆺 ｎ－ １ ｎ æ ö ＝ ３ç － １ ＋ １ － １ ＋ １ － １ ＋ ＋ １ － １ ÷ 分 è１ 􀆺 ｎ － ｎ ＋ ø 􀆺 １１ ２ ３ ３ ５ ５ ７ ２ １ ２ １ æ ö ＝ ３ç － １ ÷ < ３. 分 è１ ｎ ＋ ø 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ ２ ２ １ ２ 解法二 : 同解法一 分 (１) ꎻ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ 因为{ａ }为等差数列 ａ ＝ ｄ ＝ (２) ｎ ꎬ １ １ꎬ ２ꎬ 所以 ａ ＝ ｎ － 所以 ａ ＝ ｎ ＋ . 分 ｎ ２ １ꎬ ｎ＋ ２ ２ ３ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ ａ ｎ － 因为 ｂ ＝ ｎ ｂ ＝ ２ １ｂ 即 ｂ ( ｎ ＋ ) ＝ ( ｎ － ) ｂ ｎ＋ １ ａ ｎ ｎ ＋ ｎꎬ ｎ＋ １ ２ ３ ２ １ ｎꎬ ｎ＋ ２ ２ ３ 所以 ｂ ( ｎ ＋ ) ( ｎ ＋ ) ＝ ｂ ( ｎ － ) ( ｎ ＋ ) 分 ｎ＋ １ ２ １ ２ ３ ｎ ２ １ ２ １ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ９ 所以数列{ｂ ( ｎ － ) ( ｎ ＋ )}为常数列. ｎ ２ １ ２ １ 因此 ｂ ( ｎ － ) ( ｎ ＋ ) ＝ ｂ ＝ ｎ ２ １ ２ １ ３ １ ３ꎬ æ ö 所以 ｂ ＝ ３ ＝ ３ç １ － １ ÷ . 分 ｎ ( ｎ － ) ( ｎ ＋ ) è ｎ － ｎ ＋ ø 􀆺􀆺􀆺􀆺􀆺􀆺 １０ ２ １ ２ １ ２ ２ １ ２ １ 所以 Ｔ ＝ ｂ ＋ ｂ ＋ ｂ ＋ ＋ ｂ ＋ ｂ ｎ １ ２ ３ 􀆺 ｎ－ １ ｎ æ ö ＝ ３ç － １ ＋ １ － １ ＋ １ － １ ＋ ＋ １ － １ ÷ 分 è１ 􀆺 ｎ － ｎ ＋ ø 􀆺 １１ ２ ３ ３ ５ ５ ７ ２ １ ２ １ æ ö ＝ ３ç － １ ÷ < ３. 分 è１ ｎ ＋ ø 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ ２ ２ １ ２ . 分 ２０ (１２ ) 解析 解法一 【 】 : 依题意得 Ｘ 所有可能取值为 . 分 (１) ꎬ ２ꎬ ３ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １ æ ö ２ æ ö ２ Ｐ(Ｘ ＝ ) ＝ ç １÷ ＋ ç － １÷ ＝ １ 分 ２ è ø è１ ø ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ２ ２ ２ ２ æ ö ２æ ö æ ö æ ö ２ Ｐ(Ｘ ＝ ) ＝ Ｃ１ ç１ ÷ ç － １÷ ＋ Ｃ１ç１ ÷ ç － １÷ ＝ １ 分 ３ ２ è ø è１ ø ２è ø è１ ø ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺 ３ ２ ２ ２ ２ ２ 数学第一次教学质量检测参考答案 第 ５页 (共８页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}所以 Ｘ 的分布列为 Ｘ ２ ３ 分 ｐ １ １ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ４ ２ ２ 所以 Ｘ 的数学期望 Ｅ(Ｘ) ＝ × １ ＋ × １ ＝ ５. 分 ２ ３ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ ２ ２ ２ 若采用 局 胜制 甲最终获胜的概率为 (２) ３ ２ ꎬ : ｐ ＝ ｐ２ ＋ Ｃ１ｐ２ ( － ｐ) ＝ ｐ２ ( － ｐ) 分 １ ２ １ ３ ２ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ 若采用 局 胜制 甲最终获胜的概率为 ５ ３ ꎬ : ｐ ＝ ｐ３ ＋ Ｃ１ｐ３ ( － ｐ) ＋ Ｃ２ｐ３ ( － ｐ) ２ ＝ ｐ３ ( ｐ２ － ｐ ＋ ) 分 ２ ３ １ ４ １ ６ １５ １０ ꎬ 􀆺􀆺􀆺 ９ 若采用 局 胜制比采用 局 胜制对甲更有利 则 ｐ － ｐ > ５ ３ ３ ２ ꎬ ２ １ ０ꎬ 即 ｐ３ ( ｐ２ － ｐ ＋ ) － ｐ２ ( － ｐ) ＝ ｐ２ ( ｐ３ － ｐ２ ＋ ｐ － ＋ ｐ) ６ １５ １０ ３ ２ ６ １５ １０ ３ ２ ＝ ｐ２ ( ｐ３ － ｐ２ ＋ ｐ － ) ３ ２ ５ ４ １ ＝ ｐ２ (ｐ － ) ( ｐ２ － ｐ ＋ ) ＝ ｐ２ (ｐ － ) ２ ( ｐ － ) > ３ １ ２ ３ １ ３ １ ２ １ ０ꎬ 解得１ <ｐ < . 分 １ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ ２ 解法二 : 同解法一 分 (１) ꎻ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ５ 采用 局 胜制 不妨设赛满 局 用ξ表示 局比赛中甲获胜的局数 则 (２) ３ ２ ꎬ ３ ꎬ ３ ꎬ ξ ~ Ｂ( ｐ) ３􀆯 ꎬ 甲最终获胜的概率为 ｐ ＝ Ｐ(ξ ＝ ) ＋ Ｐ(ξ ＝ ) ＝ Ｃ２ｐ２ ( － ｐ) ＋ Ｃ３ｐ３ : １ ２ ３ ３ １ ３ ＝ ｐ２ [Ｃ２ ( － ｐ) ＋ Ｃ３ｐ] ＝ ｐ２ ( － ｐ) 分 ３ １ ３ ３ ２ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ 采用 局 胜制 不妨设赛满 局 用 η 表示 局比赛中甲获胜的局数 ５ ３ ꎬ ５ ꎬ ５ ꎬ 则 η ~ Ｂ( ｐ) ５􀆯 ꎬ 甲最终获胜的概率为 : ｐ ＝ Ｐ(η ＝ ) ＋ Ｐ(η ＝ ) ＋ Ｐ(η ＝ ) ＝ Ｃ３ｐ３ ( － ｐ) ２ ＋ Ｃ４ｐ４ ( － ｐ) ＋ Ｃ５ｐ５ ２ ３ ４ ５ ５ １ ５ １ ５ ＝ ｐ３ ( ｐ２ － ｐ ＋ ) 分 ６ １５ １０ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ９ 若采用 局 胜制比采用 局 胜制对甲更有利 则 ｐ － ｐ > ５ ３ ３ ２ ꎬ ２ １ ０ꎬ 即 ｐ３ ( ｐ２ － ｐ ＋ ) － ｐ２ ( － ｐ) ＝ ｐ２ ( ｐ３ － ｐ２ ＋ ｐ － ＋ ｐ) ６ １５ １０ ３ ２ ６ １５ １０ ３ ２ ＝ ｐ２ ( ｐ３ － ｐ２ ＋ ｐ － ) ３ ２ ５ ４ １ ＝ ｐ２ (ｐ － ) ( ｐ２ － ｐ ＋ ) ＝ ｐ２ (ｐ － ) ２ ( ｐ － ) > ３ １ ２ ３ １ ３ １ ２ １ ０ꎬ 解得１ <ｐ < . 分 １ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ ２ 数学第一次教学质量检测参考答案 第 ６页 (共８页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}. 分 ２１ (１２ ) 解析 【 】 æ ö 由题知 椭圆 Ｃ 的右焦点为 Ｆ ( ) 且过点 Ａç １ ÷ (１) ꎬ ２ ３􀆯０ ꎬ è ３􀆯 ø ꎬ ２ 所以 ａ ＝ ( ＋ ) ２ ＋ １ ＋ １ ＝ 所以 ａ ＝ . 分 ２ ３ ３ ４ꎬ ２ 􀆺􀆺􀆺􀆺􀆺􀆺 ２ ４ ４ 又 ｃ ＝ 所以 ｂ ＝ ａ２ － ｃ２ ＝ 分 ３ꎬ １ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ３ ｘ２ 所以 Ｃ 的方程为 ＋ ｙ２ ＝ . 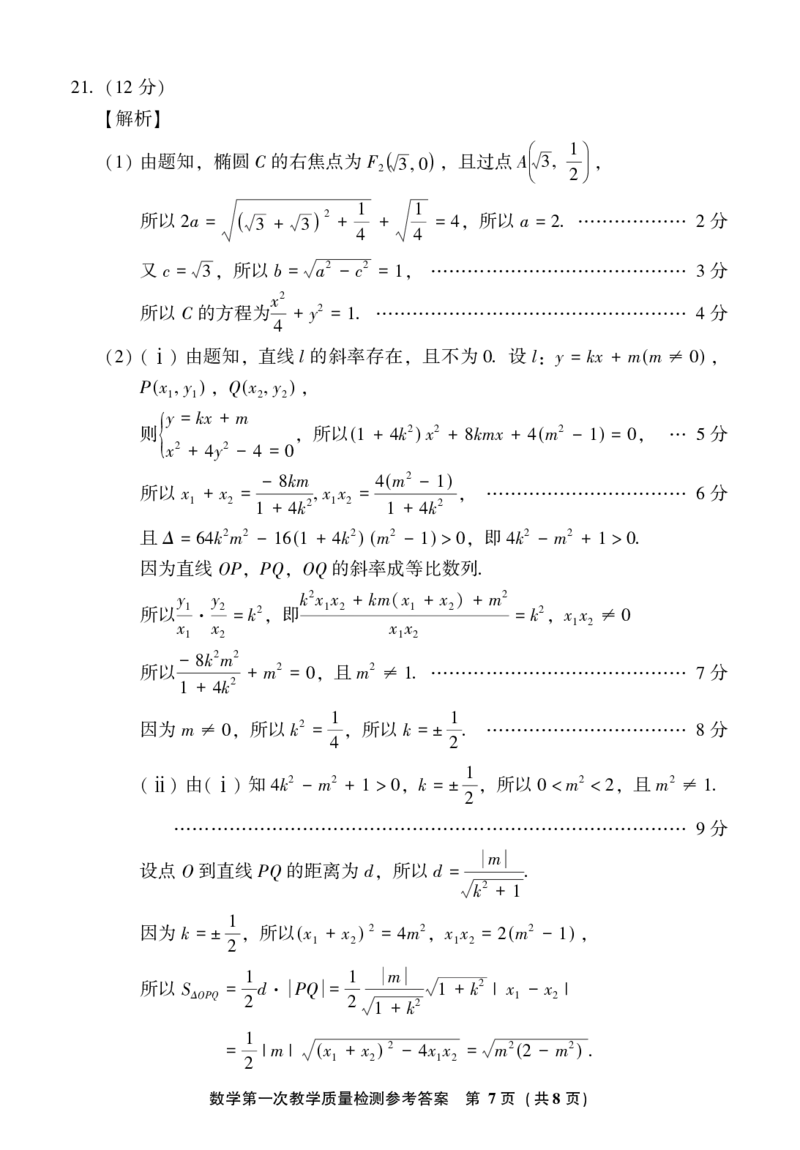分 １ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ４ ４ 由题知 直线 ｌ 的斜率存在 且不为 . 设 ｌ ｙ ＝ ｋｘ ＋ ｍ(ｍ ) (２) (ⅰ) ꎬ ꎬ ０ : ≠０ ꎬ Ｐ(ｘ ｙ ) Ｑ(ｘ ｙ ) １􀆯 １ ꎬ ２􀆯 ２ ꎬ {ｙ ＝ ｋｘ ＋ ｍ 则 所以( ＋ ｋ２ ) ｘ２ ＋ ｋｍｘ ＋ (ｍ２ － ) ＝ 分 ｘ２ ＋ ｙ２ － ＝ ꎬ １ ４ ８ ４ １ ０ꎬ 􀆺 ５ ４ ４ ０ － ｋｍ (ｍ２ － ) 所以 ｘ ＋ ｘ ＝ ８ ｘ ｘ ＝ ４ １ 分 １ ２ ＋ ｋ２ 􀆯 １ ２ ＋ ｋ２ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ６ １ ４ １ ４ 且 Δ ＝ ｋ２ｍ２ － ( ＋ ｋ２ ) (ｍ２ － ) > 即 ｋ２ － ｍ２ ＋ > . ６４ １６ １ ４ １ ０ꎬ ４ １ ０ 因为直线 ＯＰ ＰＱ ＯＱ 的斜率成等比数列. ꎬ ꎬ ｙ ｙ ｋ２ｘ ｘ ＋ ｋｍ ｘ ＋ ｘ ＋ ｍ２ 所以 １ ２ ＝ ｋ２ 即 １ ２ ( １ ２) ＝ ｋ２ ｘ ｘ ｘ 􀅰ｘ ꎬ ｘ ｘ ꎬ １ ２ ≠０ １ ２ １ ２ － ｋ２ｍ２ 所以 ８ ＋ ｍ２ ＝ 且 ｍ２ . 分 ＋ ｋ２ ０ꎬ ≠１ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ １ ４ 因为 ｍ 所以 ｋ２ ＝ １ 所以 ｋ ＝ ± １. 分 ≠０ꎬ ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ８ ４ ２ 由 知 ｋ２ － ｍ２ ＋ > ｋ ＝ ± １ 所以 <ｍ２ < 且 ｍ２ . (ⅱ) (ⅰ) ４ １ ０ꎬ ꎬ ０ ２ꎬ ≠１ ２ 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ９ ｍ 设点 Ｏ 到直线 ＰＱ 的距离为 ｄ 所以 ｄ ＝ . ꎬ ｋ２ ＋ １ 因为 ｋ ＝ ± １ 所以(ｘ ＋ ｘ ) ２ ＝ ｍ２ ｘ ｘ ＝ (ｍ２ － ) ꎬ １ ２ ４ ꎬ １ ２ ２ １ ꎬ ２ ｍ 所以 Ｓ ＝ １ｄ ＰＱ ＝ １ ＋ ｋ２ ｜ ｘ － ｘ ｜ ΔＯＰＱ ２ 􀅰 ２ ＋ ｋ２ １ １ ２ １ ＝ １ ｜ ｍ ｜ (ｘ ＋ ｘ ) ２ － ｘ ｘ ＝ ｍ２ ( － ｍ２ ) . １ ２ ４ １ ２ ２ ２ 数学第一次教学质量检测参考答案 第 ７页 (共８页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}＝ － ｍ２ － ２ ＋ ( １) １ꎬ 又 < ｍ２ < 且 ｍ２ . 所以 Ｓ ０ ２ꎬ ≠１ △ ＯＰＱ∈(０ꎬ １) 即 ＯＰＱ 的面积的取值范围 . 分 △ (０ꎬ １) 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ . 分 ２２ (１２ ) 解析 【 】 依题意 得 ｆ ′(ｘ) ＝ ａ ｘ ＋ . 分 (１) ꎬ ｅ １ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １ 当 ａ 时 ｆ ′(ｘ) > 所以 ｆ(ｘ) 在(－ ＋ ) 单调递增. 分 ≥０ ꎬ ０ꎬ ∞􀆯 ∞ 􀆺􀆺􀆺􀆺 ２ 当 ａ < 时 令 ｆ ′(ｘ) > 可得 ｘ < － (－ ａ) ０ ꎬ ０ꎬ ｌｎ ꎻ 令 ｆ ′(ｘ) < ０ꎬ 可得 ｘ > － (－ ａ) ｌｎ ꎬ 所以 ｆ(ｘ) 在(－ － (－ ａ) ) 单调递增 在(－ (－ ａ) ＋ ) 单调递减. ∞􀆯 ｌｎ ꎬ ｌｎ 􀆯 ∞ 分 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ４ 综上所述 当 ａ 时 ｆ(ｘ) 在(－ ＋ ) 单调递增 当 ａ < 时 ｆ(ｘ) 在 ꎬ ≥０ ꎬ ∞􀆯 ∞ ꎻ ０ ꎬ (－ － (－ ａ) ) 单调递增 在(－ (－ ａ) ＋ ) 单调递减. 分 ∞􀆯 ｌｎ ꎬ ｌｎ 􀆯 ∞ 􀆺􀆺􀆺 ５ ｘ － ｘ － 因为当 ｘ > 时 ｆ(ｘ) > １ ＋ ｘ 所以 ａ ｘ ＋ ｘ ＋ > １ ＋ ｘ (２) １ ꎬ ｌｎ ａ ꎬ ｅ １ ｌｎ ａ ꎬ 即 ｌｎ ａ ｘ ＋ ｘ ＋ > (ｘ － ) － ａ ＋ ｘ ｅ ｅ １ ｌｎ １ ｌｎ ꎬ 即 ｘ＋ ｌｎ ａ ＋ ａ ＋ ｘ > (ｘ － ) ＋ ｘ － ｅ ｌｎ ｌｎ １ １ꎬ 即 ｘ＋ ｌｎ ａ ＋ ｘ ＋ ａ > ｌｎ (ｘ－ １ ) ＋ (ｘ － ) . 分 ｅ ｌｎ ｅ ｌｎ １ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ７ 令 ｈ(ｘ) ＝ ｘ ＋ ｘ 则有 ｈ(ｘ ＋ ａ) >ｈ( (ｘ － ) ) 对 ｘ ( ＋ ) 恒成立. ｅ ꎬ ｌｎ ｌｎ １ ∀ ∈ １􀆯 ∞ 因为 ｈ′(ｘ) ＝ ｘ ＋ > 所以 ｈ(ｘ) 在(－ ＋ ) 单调递增 分 ｅ １ ０ꎬ ∞􀆯 ∞ ꎬ 􀆺􀆺􀆺 ８ 故只需 ｘ ＋ ａ > (ｘ － ) ｌｎ ｌｎ １ ꎬ 即 ａ > (ｘ － ) － ｘ 对 ｘ ( ＋ ) 恒成立. 分 ｌｎ ｌｎ １ ∀ ∈ １􀆯 ∞ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 ９ － ｘ 令 Ｆ(ｘ) ＝ (ｘ － ) － ｘ 则 Ｆ′(ｘ) ＝ １ － ＝ ２ 令 Ｆ′(ｘ) ＝ ｌｎ １ ꎬ ｘ － １ ｘ － ꎬ ０ꎬ １ １ 得 ｘ ＝ . ２ 当 ｘ ( ) 时 Ｆ′(ｘ) > 当 ｘ ( ＋ ) 时 Ｆ′(ｘ) < ∈ １􀆯２ ꎬ ０ꎬ ∈ ２􀆯 ∞ ꎬ ０ꎬ 所以 Ｆ(ｘ) 在( ) 单调递增 在( ＋ ) 单调递减 １􀆯２ ꎬ ２􀆯 ∞ ꎬ 所以 Ｆ(ｘ) Ｆ( ) ＝－ . 分 ≤ ２ ２ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １１ 因此 ａ > － 所以 ａ > １. 分 ｌｎ ２ꎬ 􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺􀆺 １２ ２ ｅ 数学第一次教学质量检测参考答案 第 ８页 (共８页) {#{QQABYYSUogggQgAAARhCEQGACAGQkAACCAgOBAAMMAAByANABAA=}#}