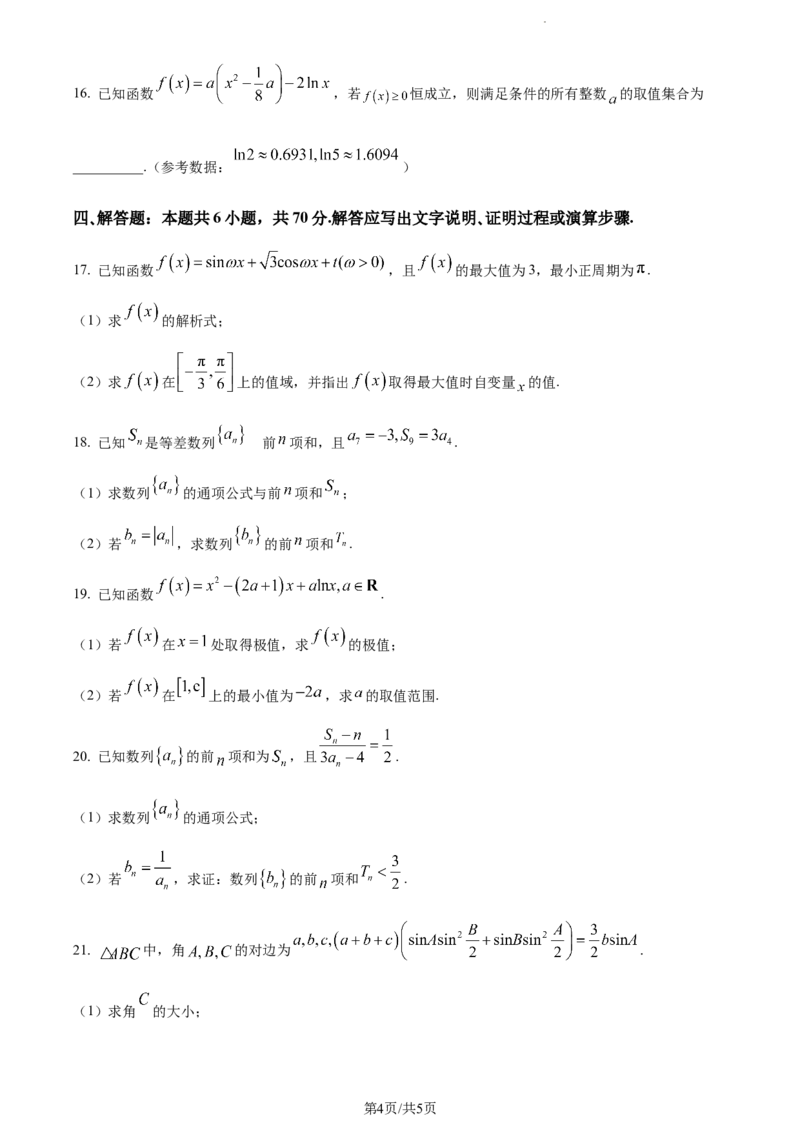文档内容
2024 届高三五校联盟 10 月学情调查测试
数学试题
试卷满分:150分 考试时长:120分钟
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1. 已知集合 ,则 ( )
A. B. C. D.
2. 已知复数 满足 ,则 ( )
A. B. C. D.
3. 已知 ,命题 ,命题 ,则 是 的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 数学家杨辉在其专著《详解九章算术法》和《算法通变本末》中,提出了一些新的高阶等差数列.其中
二阶等差数列是一个常见的高阶等差数列,如数列 从第二项起,每一项与前一项的差组成的
新数列 是等差数列,则称数列 为二阶等差数列.现有二阶等差数列 ,其前六项分
别为 ,则 的最小值为( )
A. B. C. 1 D.
5. 已知 为锐角, ,则 ( )
第1页/共5页
学科网(北京)股份有限公司A. B. C. D.
6. 已知函数 ,则使不等式 成立的 的取值范围是( )
.
A B.
C. D.
7. 已知等差数列 和等差数列 的前 项和分别为 和 ,且 ,则使得 为整数的
正整数 的个数为( )
A. 6 B. 7 C. 8 D. 9
8. 已知 ,则 的值为( )
A. B. C. D.
二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知 为等比数列, 是其前 项和.若 与 等的差中项为20,则( )
A. B. 公比
C. D.
10. 已知正数 满足 ,则( )
A. 的最大值为 B. 的最小值为9
C. 的最小值为 D. 的最小值为
第2页/共5页
学科网(北京)股份有限公司11. 已知函数 ,则( )
A. 的图象关于原点中心对称
B. 在区间 上的最小值为
C. 过点 有且仅有1条直线与曲线 相切
D. 若过点 存在3条直线与曲线 相切,则实数 的取值范围是
12. 已知函数 ,则( )
A. 是方程 的两个不等实根,且 最小值为 ,则
B. 若 在 上有且仅有4个零点,则
C. 若 在 上单调递增,则 在 上的零点最多有3个
D. 若 的图象与直线 连续的三个公共点从左到右依次为 ,若
,则
三、填空题:本题共4小题,每小题5分,共20分.
13. 数列 满足 ,则 __________.
14. 已知函数 ,若 在区间 上单调递增,则实数 的取值范围是
__________.
的
15. 在 中,角 对边分别为 为 边中点,若 ,则 面
积 的最大值为__________.
第3页/共5页
学科网(北京)股份有限公司16. 已知函数 ,若 恒成立,则满足条件的所有整数 的取值集合为
__________.(参考数据: )
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知函数 ,且 的最大值为3,最小正周期为 .
(1)求 的解析式;
(2)求 在 上的值域,并指出 取得最大值时自变量 的值.
18. 已知 是等差数列 前的项和,且 .
(1)求数列 的通项公式与前 项和 ;
(2)若 ,求数列 的前 项和 .
19. 已知函数 .
(1)若 在 处取得极值,求 的极值;
(2)若 在 上的最小值为 ,求 的取值范围.
20. 已知数列 的前 项和为 ,且 .
(1)求数列 的通项公式;
(2)若 ,求证:数列 的前 项和 .
21. 中,角 的对边为 .
(1)求角 的大小;
第4页/共5页
学科网(北京)股份有限公司(2)若 内切圆的半径 ,求 的面积.
22. 已知函数 .
(1)若函数 在点 处的切线与函数 的图象有公共点,求实数 的取值范围;
(2)若函数 和函数 的图象没有公共点,求实数 的取值范围.
第5页/共5页
学科网(北京)股份有限公司