文档内容
蚌埠市 2024届高三年级第三次教学质量检查考试
数学参考答案及评分标准
一、选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题
目要求的。
题 号 1 2 3 4 5 6 7 8
答 案 A D A B C B C B
二、选择题:本题共3小题,每小题6分,共18分。在每小题给出的选项中,有多项符合题目要求。
全部选对的得6分,部分选对的得部分分,有选错的得0分。
题 号 9 10 11
答 案 ABC BC ABD
三、填空题:本题共3小题,每小题5分,共15分。
12(0,1)
130或4;(2-槡2,2+槡2)∪{4}(答对第一空给2分,答对第二空给3分)
141
四、解答题:本题共5个小题,共77分。解答应写出说明文字、证明过程或演算步骤。
15(13分)
b
解:(1)由题意知a=1,且 =1,∴b=1,……………………………………………… 2分
a
∴c=槡a2+b2=槡2,
c
所以双曲线的离心率e= =槡2……………………………………………… 5分
a
(2)由(1)知双曲线方程为x2-y2=1,
1 1
将y= x- 即x-1=2y代入x2-y2=1,得3y2+4y=0, ………………… 9分
2 2
4
因而y=0,y=- ,
1 2 3
4
所以|PQ|=槡1+22· y-y = 槡5……………………………………… 13分
1 2 3
16(15分)
解:(1)依题意,p=1,p=05,
1 2
p=p×05+(1-p)×(1-04)=06-01p=055 …………………… 6分
3 2 2 2
依题意p=p ×05+(1-p )×(1-04)=06-01p
n n-1 n-1 n-1
6 1( 6) 6 5
整理得p- =- p - ,又p- = ≠0,
n 11 10 n-1 11 1 11 11
蚌埠市高三年级数学参考答案第1页(共4页)
{#{QQABQYKAgggoAAAAAQgCEwGaCgIQkBCACKoGBEAAMAABCBFABAA=}#}{ 6} 5 1
所以 p- 是首项为 ,公比为- 的等比数列………………………… 9分
n 11 11 10
5( 1)n-1 6
(2)由(1),寒假第n天不下雪的概率p= - + ,…………………… 11分
n 11 10 11
从而小明寒假第n天跑步的概率为
23 2( 1)n-1
q=p×06+(1-p)×02=02+04p= + - ,…………… 13分
n n n n 55 11 10
则他第n天通过运动锻炼消耗能量为
1
330q+220(1-q)=220+110q=266+20(- )n-1 …………………… 15分
n n n 10
17(15分)
解:(1)由题意知AD=BC=PA=2,则在△ABC中,
AB2+BC2-AC2 42+22-(2槡7)2 1
cos∠ABC= = =- ,
2AB·BC 2×4×2 2
2π π
∵∠ABC∈(0,π)∴∠ABC= ,从而∠DAB= ,…………………………… 3分
3 3
π 1
△ABD中,BD2=AD2+AB2-2AD·AB·cos =22+42-2×2×4× =12,
3 2
则BD2+AD2=12+4=16=AB2
∴BD⊥AD, ……………………………………………………………………… 5分
又BD⊥AE,AD∩AE=A,所以BD⊥平面PAD,
而BD平面ABCD,
∴平面PAD⊥平面ABCD……………………………………………………… 8分
(2)由(1)知 BD⊥平面 PAD,PD平面 PAD,
∴BD⊥PD,
∴PD=槡PB2-BD2=2,
所以△PAD为等边三角形,……… 10分
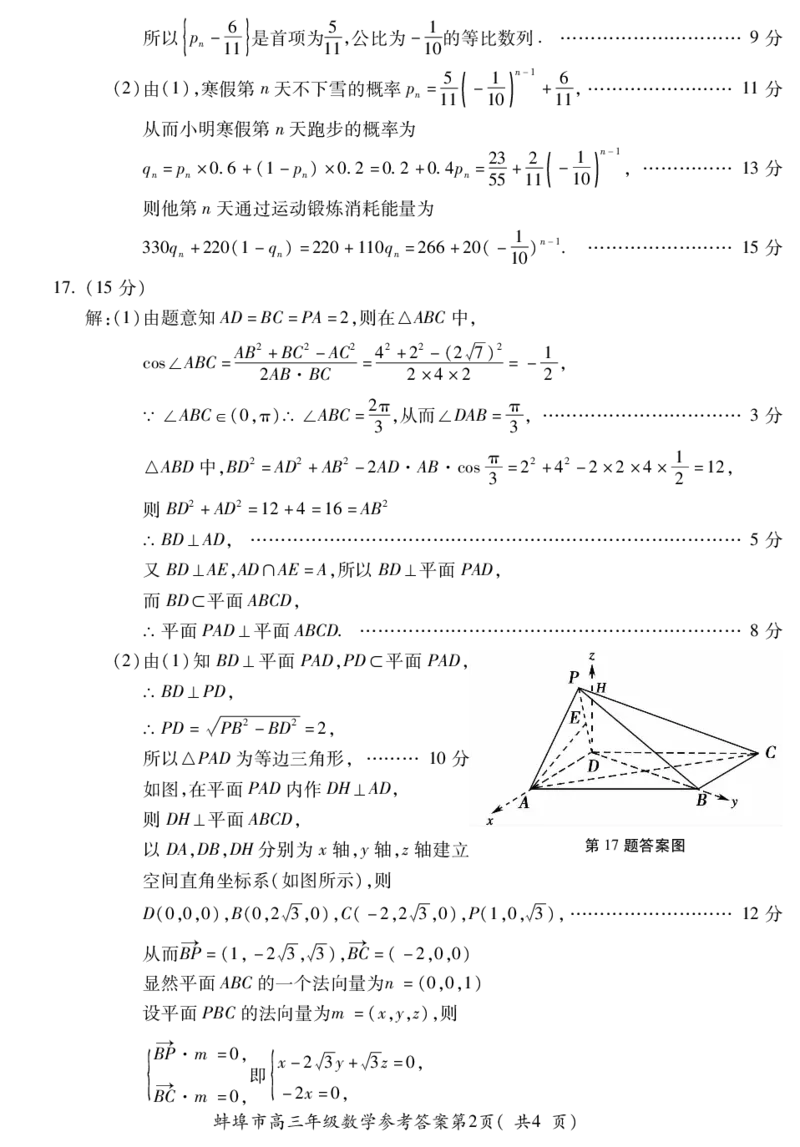
如图,在平面PAD内作DH⊥AD,
则DH⊥平面ABCD,
以DA,DB,DH分别为 x轴,y轴,z轴建立 第17题答案图
空间直角坐标系(如图所示),则
D(0,0,0),B(0,2槡3,0),C(-2,2槡3,0),P(1,0,槡3),……………………… 12分
→ →
从而BP=(1,-2槡3,槡3),BC=(-2,0,0)
显然平面ABC的一个法向量为n=(0,0,1)
设平面PBC的法向量为m=(x,y,z),则
→
{BP·m=0, {x-2槡3y+槡3z=0,
即
→
BC·m=0, -2x=0,
蚌埠市高三年级数学参考答案第2页(共4页)
{#{QQABQYKAgggoAAAAAQgCEwGaCgIQkBCACKoGBEAAMAABCBFABAA=}#}取m=(0,1,2),
记二面角P-BC-A的平面角为α,则
|m·n| 1×2 2槡5
cosα= cos〈m,n〉 = = =
|m|·|n| 1×槡5 5
2槡5
即二面角P-BC-A的余弦值为 ……………………………………… 15分
5
18(17分)
1
解:(1)记g(x)=tanx-x,则g′(x)= -1, ……………………………………… 2分
cos2x
( π)
因为x∈ 0, ,所以cosx∈(0,1),所以g′(x)>0,
2
所以g(x)单调递增,
从而g(x)>g(0)=0,即tanx>x……………………………………………… 4分
当a=1时x>xf(x)等价于x>sinx,记h(x)=x-sinx,
则h′(x)=1-cosx>0,h(x)单调递增, ……………………………………… 6分
所以h(x)>h(0)=0,即x>sinx
( π)
综上,当a=1,x∈ 0, 时,tanx>x>xf(x)………………………………… 8分
2
x x asinx x asinx
(2) <f(x)等价于 < ,记F(x)= - ,
tanx tanx x tanx x
则F(-x)=F(x),
( π)
所以题设等价于当x∈ 0, 时,F(x)<0即x2cosx-asin2x<0
2
当a≤0时,F(x)>0,不合题意……………………………………………… 10分
当0<a<1时,x2cosx-asin2x>x2cosx-ax2=x2(cosx-a)
( π)
存在θ∈ 0, ,cosθ-a=0,
2
因此当x∈(0,θ),x2cosx-asin2x>0,即F(x)<0不成立,不合题意 …… 13分
当 a≥1时,x2cosx-asin2x≤x2cosx-sin2x,
( π)
记G(x)=x2cosx-sin2x,x∈ 0, ,由于tanx>x,所以sinx>xcosx,故
2
G′(x)=2xcosx-x2sinx-2sinxcosx<2sinx-x2sinx-2sinxcosx
=-sinx[x2-2(1-cosx)]=-sinx
(
x2-4sin2
x)
=-4sinx
[(x)2
-sin2
x]
<0
2 2 2
( π)
从而G(x)在 0, 单调递减,G(x)<G(0)=0,F(x)<0恒成立,符合题意
2
综上,实数a的取值范围是[1,+∞) ……………………………………… 17分
蚌埠市高三年级数学参考答案第3页(共4页)
{#{QQABQYKAgggoAAAAAQgCEwGaCgIQkBCACKoGBEAAMAABCBFABAA=}#}19(17分)
解:(1)令x=0,则e(0)=1
由e(x)e(y)=e(x+y),令y=-x,则e(x)e(-x)=e(0)=1
1
因为e(x)≠0,故e(-x)= ……………………………………………… 5分
e(x)
(ix)4n (-ix)4n x4n x4n 2x4n
(2)证明:因为 + = + = ,
(4n)! (4n)! (4n)! (4n)! (4n)!
(ix)4n+1 (-ix)4n+1 ix4n+1 -ix4n+1
+ = + =0,
(4n+1)! (4n+1)! (4n+1)! (4n+1)!
(ix)4n+2 (-ix)4n+2 -x4n+2 -x4n+2 -2x4n+2
+ = + = ,
(4n+2)! (4n+2)! (4n+2)! (4n+2)! (4n+2)!
(ix)4n+3 (-ix)4n+3 -ix4n+3 ix4n+3
+ = + =0,
(4n+3)! (4n+3)! (4n+3)! (4n+3)!
e(ix)+e(-ix)=∑ ∞ [2x4n - 2x4n+2 ] =∑ ∞ 2(-1)k x2k=2∑ ∞ (-1)k x2k=2c(x),
n=0 (4n)! (4n+2)! k=0 (2k)! k=0(2k)!
e(ix)+e(-ix)
所以c(x)= …………………………………………………… 11分
2
x
(3)证明:令g(x)= ,则有
e(x)-1
-x x [ 1 1 ]
g(-x)-g(x)= - =-x +
e(-x)-1 e(x)-1 e(-x)-1 e(x)-1
[e(x)-1]+[e(-x)-1] e(x)+e(-x)-2
=-x· =-x· =x,………… 14分
[e(-x)-1][e(x)-1] 2-e(x)-e(-x)
∞ B ∞ B
因此x=g(-x)-g(x)=∑ n(-x)n-∑ nxn
n=0n! n=0n!
=-2∑ ∞ B 2k+1 x2k+1=-2 [ Bx+∑ ∞ B 2k+1 x2k+1 ]
k=0(2k+1)! 1
k=1
(2k+1)!
1 ∞ B
故B=- 且∑ 2k+1 x2k+1=0,即B =0(k=1,2,3,…)………… 17分
1 2 k=1(2k+1)! 2k+1
(以上答案仅供参考,其它做法请参考以上评分标准赋分)
蚌埠市高三年级数学参考答案第4页(共4页)
{#{QQABQYKAgggoAAAAAQgCEwGaCgIQkBCACKoGBEAAMAABCBFABAA=}#}