文档内容
秘密★启用前
2024-2025(上)8 月月度质量监测暨第零次诊断测试
高 三 数 学
本试卷满分150分 考试时间120分钟
命题人:陈建骐、林晓萍、刘光辉 校题人:刘梦娜、罗鑫、黄伟
【命题单位:辽宁沈文新高考研究联盟】
第Ⅰ卷 选择题(共 58 分)
一、单选题(本大题共 8 小题,每小题 5 分,共 40 分,在每小题所给的四个选项中,有
且只有一项是符合题目要求的)
1.已知集合 , , .则 的子集共有
A.1个 B.2个 C.3个 D.4个
𝑀𝑀 ={0,1,2,3,4} 𝑁𝑁 ={1,3,5} 𝑃𝑃 =𝑀𝑀∩𝑁𝑁 𝑃𝑃
2.已知复数 ,则
√2+√2𝑖𝑖
𝑧𝑧 = 1−𝑖𝑖 |𝑧𝑧|=
A. B. C.2 D.
√2
√2 2 2√2
3.椭圆 的焦点的坐标为
2 2
𝑥𝑥 𝑦𝑦
A.5 + 9 =1, B. ,
C. , , , D. ,
�−√14,0� �√14,0� (−2,0) (2,0)
4.把 14 个相同的球全部放入编号为 1、2、3 的三个盒内,要求盒内的球数不小于盒号数,
�0 −√14� �0 √14� (0,−2) (0,2)
则不同的放入方法种数为
A.36 B.45 C.72 D.165
5.下图是一个圆台的侧面展开图,若两个半圆的半径分别是1和2,则该圆台的体积是
A. B. C. D.
7√2𝜋𝜋 7√3𝜋𝜋 7√2𝜋𝜋 7√3𝜋𝜋
6.若函数24 为R上的奇函2数4,且当 时, 12 ,则 12
A. B. C. D.−1
𝑓𝑓(𝑥𝑥) 𝑥𝑥 >0 𝑓𝑓(𝑥𝑥)=2𝑥𝑥−1 𝑓𝑓(0)+𝑓𝑓(−1)=
{a a }
7.已知−数4列 满足 −,3 −2,则数列 n n+1 的前100项的和是
1
{𝑎𝑎𝑛𝑛} 𝑎𝑎1 =2 𝑎𝑎𝑛𝑛+1−𝑎𝑎𝑛𝑛+𝑎𝑎𝑛𝑛𝑎𝑎𝑛𝑛+1 =0
A. B. C. D.
25 50 99 100
8.声音5是1由物体振动产生的10声1 波,我们听到的声音2中02包含着正弦函数.若某101声音对应的函
数可近似为 ,则下列叙述正确的是
1
高三数学 第 1 页,共 3 页
𝑓𝑓(𝑥𝑥)=𝑠𝑠𝑠𝑠𝑠𝑠𝑥𝑥+2𝑠𝑠𝑠𝑠𝑠𝑠2𝑥𝑥
学科网(北京)股份有限公司A. 为 的对称轴 B. 为 的对称中心
𝜋𝜋 3𝜋𝜋
𝑥𝑥 = 2 𝑓𝑓(𝑥𝑥) �2 ,0� 𝑓𝑓(𝑥𝑥)
D. 在区间 上单调递增
C. 在区间 上有3个零点
5𝜋𝜋 7𝜋𝜋
二、多选
𝑓𝑓
题
(𝑥𝑥
(
)
本大题
[0
共
,10
3
]
小题,每小题 6 分,共 1𝑓𝑓8(𝑥𝑥分) ,在每�小3题, 3所�给的四个选项中,有
多项符合题目要求。全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.给出下列说法,其中正确的是
A.数据0,1,2,4的极差与中位数之积为6
B.已知一组数据 的方差是 5,则数据 的方差是
20
𝑥𝑥1,𝑥𝑥2,⋯,𝑥𝑥𝑛𝑛 4𝑥𝑥1−1,4𝑥𝑥2−1,⋯,4𝑥𝑥𝑛𝑛−1
C.已知一组数据 的方差为0,则此组数据的众数唯一
D.已知一组不完全相同的数据 的平均数为 ,在这组数据中加入一个数
𝑥𝑥1,𝑥𝑥2,⋯,𝑥𝑥𝑛𝑛
后得到一组新数据 ,其平均数为 ,则
𝑥𝑥1,𝑥𝑥2,⋯,𝑥𝑥𝑛𝑛 𝑥𝑥0
10.已知直线 经过抛物线 的焦点,且与 交于 A,B两点,以线段 为
𝑥𝑥0 𝑥𝑥0,𝑥𝑥1,𝑥𝑥2,⋯,𝑥𝑥𝑛𝑛 𝑥𝑥 𝑥𝑥 =𝑥𝑥0
直径的 与 的准线相切于点2 ,则
𝑙𝑙 𝐶𝐶:𝑦𝑦 =2𝑝𝑝𝑥𝑥(𝑝𝑝>0) 𝐶𝐶 𝐴𝐴𝐴𝐴
⊙𝐷𝐷 𝐶𝐶 𝑃𝑃(−2,−1) B.点 的坐标为
A.直线 的方程为
7
𝐷𝐷 �4,−1�
C. 的𝑙𝑙 周长为 4𝑥𝑥 +𝑦𝑦−8=0
D.直线 与 相切
17
⊙𝐷𝐷 2 𝜋𝜋
11.已知函数 , 是自然对数的底数,则 4𝑥𝑥+2𝑦𝑦+9=0 ⊙𝐷𝐷
𝑙𝑙𝑛𝑛𝑥𝑥
A. 𝑓𝑓(𝑥𝑥) = 𝑥𝑥 𝑒𝑒
B. √11
2 <11
C.若 𝜋𝜋 ,2则 𝜋𝜋
2𝑙𝑙𝑠𝑠3 >3𝑙𝑙𝑠𝑠𝜋𝜋 >3𝑙𝑙𝑠𝑠2
D. 𝑥𝑥1 𝑥𝑥2 ,且 ,则
𝑥𝑥2 =𝑥𝑥1 𝑥𝑥1+𝑥𝑥2 =2𝑒𝑒
𝑓𝑓(𝑥𝑥1)=𝑓𝑓(𝑥𝑥2) 𝑥𝑥1 ≠𝑥𝑥2 𝑙𝑙𝑠𝑠𝑥𝑥1+𝑙𝑙𝑠𝑠𝑥𝑥2 >2
第Ⅱ卷 非选择题(共 92 分)
三、填空题(本大题共3小题,每小题5分,共15 分)
12.若 为锐角, ,则 .
4
13.若向𝛼𝛼 量 sin𝛼𝛼 =,5 cos(𝜋𝜋,+则𝛼𝛼)=在 上的投影向量为 .
14.在三棱锥 中,已知 , , ,平面 平面 ,
𝑎𝑎⃗ =�√3,3� 𝑏𝑏�⃗ =(−2,0) 𝑎𝑎⃗ 𝑏𝑏�⃗
且 ,则以下结论正确的是 (填序号).
𝐷𝐷−𝐴𝐴𝐴𝐴𝐶𝐶 𝐴𝐴𝐴𝐴 =𝐴𝐴𝐶𝐶 =2 𝐴𝐴𝐶𝐶 =2√3 𝐷𝐷𝐴𝐴 =4 𝐴𝐴𝐶𝐶𝐷𝐷 ⊥ 𝐴𝐴𝐴𝐴𝐶𝐶
① ②平面 平面
𝐷𝐷𝐴𝐴 ⊥𝐴𝐴𝐶𝐶
③𝐷𝐷三𝐴𝐴棱⊥锥𝐴𝐴𝐶𝐶 的体积为 𝐷𝐷𝐴𝐴𝐴𝐴 ⊥ 𝐴𝐴𝐴𝐴𝐶𝐶
④三棱锥 的外接球的表面积为
4√3
四、解答题(本𝐷𝐷−大𝐴𝐴题𝐴𝐴共𝐶𝐶 5 小题,3共 77 分。解答时应写出
𝐷𝐷
必
−
要
𝐴𝐴𝐴𝐴
的
𝐶𝐶
文字说明、证明过程或
32
演
𝜋𝜋
算步骤)
15.有 4 名同学下课后一起来到图书馆看书,到图书馆以后把书包放到了一起,后来停电
了,大家随机拿起了一个书包离开图书馆,分别计算下列事件的概率.
(1)恰有两名同学拿对了书包;
(2)至少有两名同学拿对了书包;
(3)书包都拿错了.
高三数学 第 2 页,共 3 页
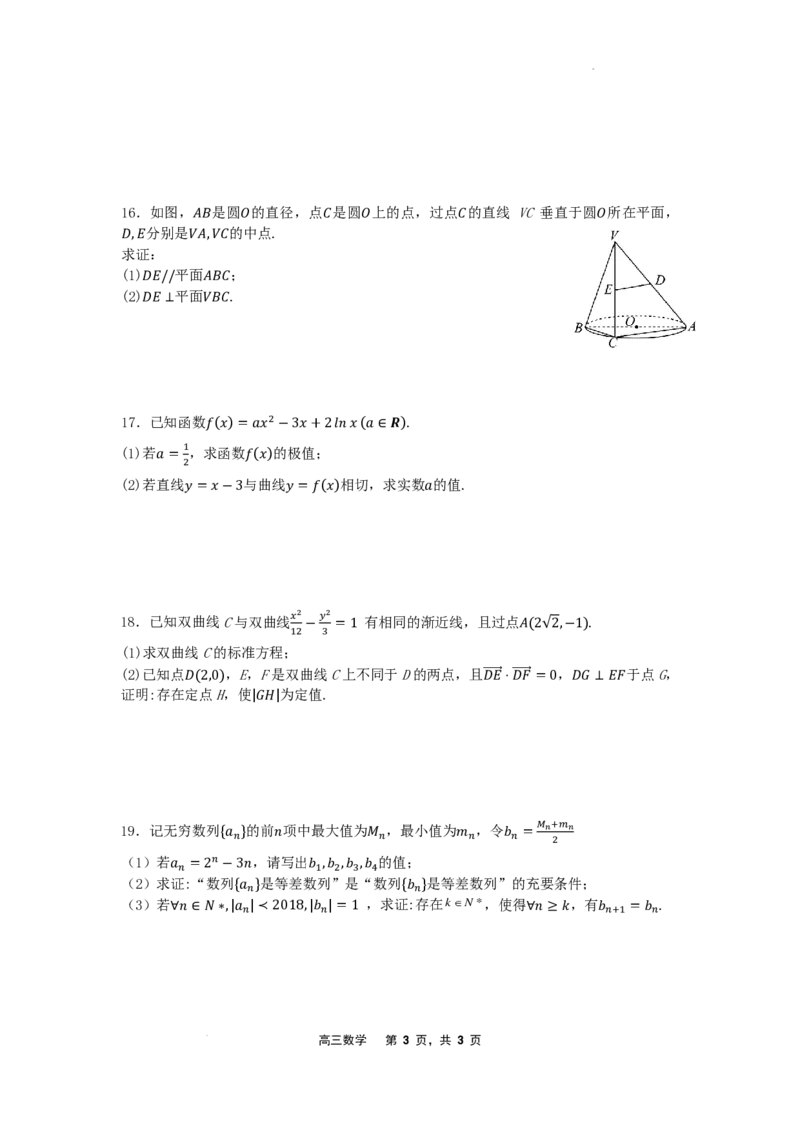
学科网(北京)股份有限公司16.如图, 是圆 的直径,点 是圆 上的点,过点 的直线 VC垂直于圆 所在平面,
分别是 的中点.
𝐴𝐴𝐴𝐴 𝑂𝑂 𝐶𝐶 𝑂𝑂 𝐶𝐶 𝑂𝑂
求证:
𝐷𝐷,𝐸𝐸 𝑉𝑉𝐴𝐴,𝑉𝑉𝐶𝐶
(1) 平面 ;
(2) 平面 .
𝐷𝐷𝐸𝐸// 𝐴𝐴𝐴𝐴𝐶𝐶
𝐷𝐷𝐸𝐸 ⊥ 𝑉𝑉𝐴𝐴𝐶𝐶
17.已知函数 .
2
(1)若 ,求𝑓𝑓(函𝑥𝑥)数=𝑎𝑎𝑥𝑥 的−极3𝑥𝑥值+;2 𝑙𝑙𝑠𝑠𝑥𝑥(𝑎𝑎 ∈𝑹𝑹)
1
(2)若直𝑎𝑎 =线2 与𝑓𝑓(曲𝑥𝑥)线 相切,求实数 的值.
𝑦𝑦=𝑥𝑥−3 𝑦𝑦=𝑓𝑓(𝑥𝑥) 𝑎𝑎
18.已知双曲线C与双曲线 有相同的渐近线,且过点 .
2 2
𝑥𝑥 𝑦𝑦
(1)求双曲线C的标准方程;12 − 3 =1 𝐴𝐴(2√2,−1)
(2)已知点 ,E,F是双曲线C上不同于D的两点,且 , 于点G,
证明:存在定点H,使 为定值.
𝐷𝐷(2,0) 𝐷𝐷����𝐸𝐸�⃗·𝐷𝐷����𝐷𝐷�⃗ =0 𝐷𝐷𝐷𝐷 ⊥𝐸𝐸𝐷𝐷
|𝐷𝐷𝐺𝐺|
19.记无穷数列 的前 项中最大值为 ,最小值为 ,令
𝑀𝑀𝑛𝑛+𝑚𝑚𝑛𝑛
(1)若 {𝑎𝑎𝑛𝑛} ,请𝑠𝑠写出 𝑀𝑀的𝑛𝑛 值; 𝑚𝑚𝑛𝑛 𝑏𝑏𝑛𝑛 = 2
(2)求证:“数𝑛𝑛列 是等差数列”是“数列 是等差数列”的充要条件;
𝑎𝑎𝑛𝑛 =2 −3𝑠𝑠 𝑏𝑏1,𝑏𝑏2,𝑏𝑏3,𝑏𝑏4
(3)若 ,求证:存在k∈N*,使得 ,有 .
{𝑎𝑎𝑛𝑛} {𝑏𝑏𝑛𝑛}
∀𝑠𝑠 ∈𝑁𝑁∗,|𝑎𝑎𝑛𝑛|≺2018,|𝑏𝑏𝑛𝑛|=1 ∀𝑠𝑠 ≥𝑘𝑘 𝑏𝑏𝑛𝑛+1 =𝑏𝑏𝑛𝑛
高三数学 第 3 页,共 3 页
学科网(北京)股份有限公司