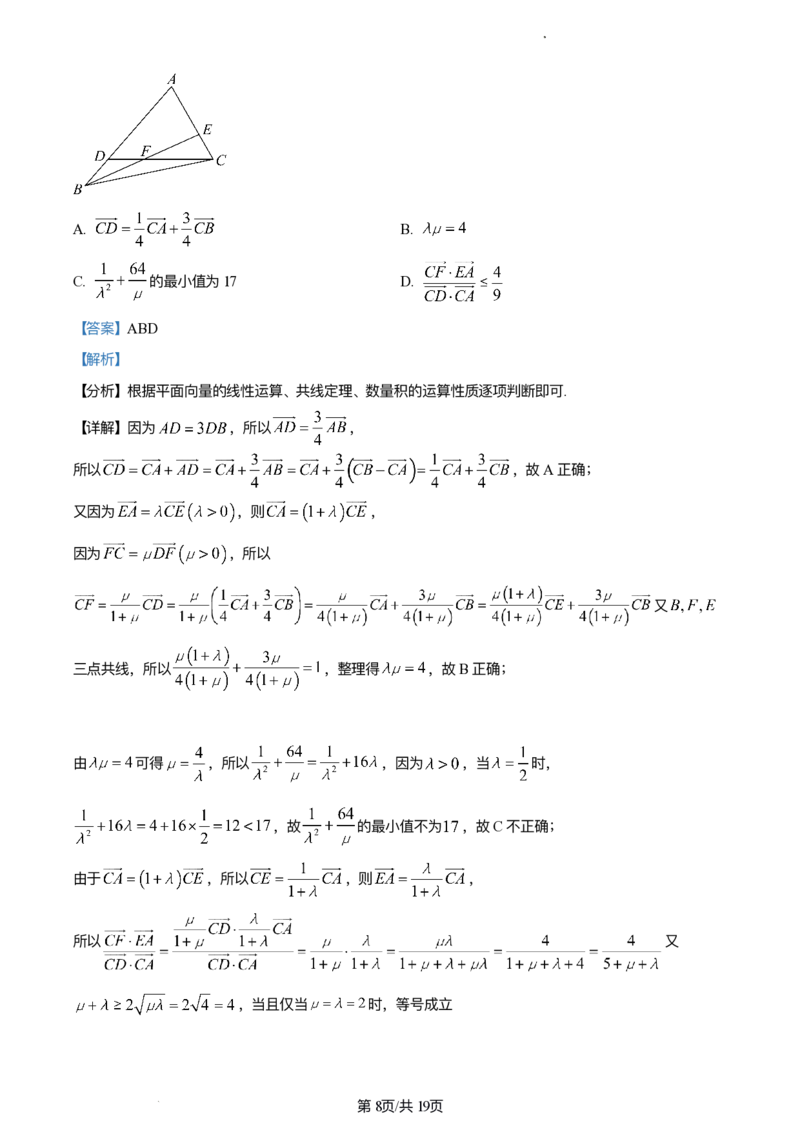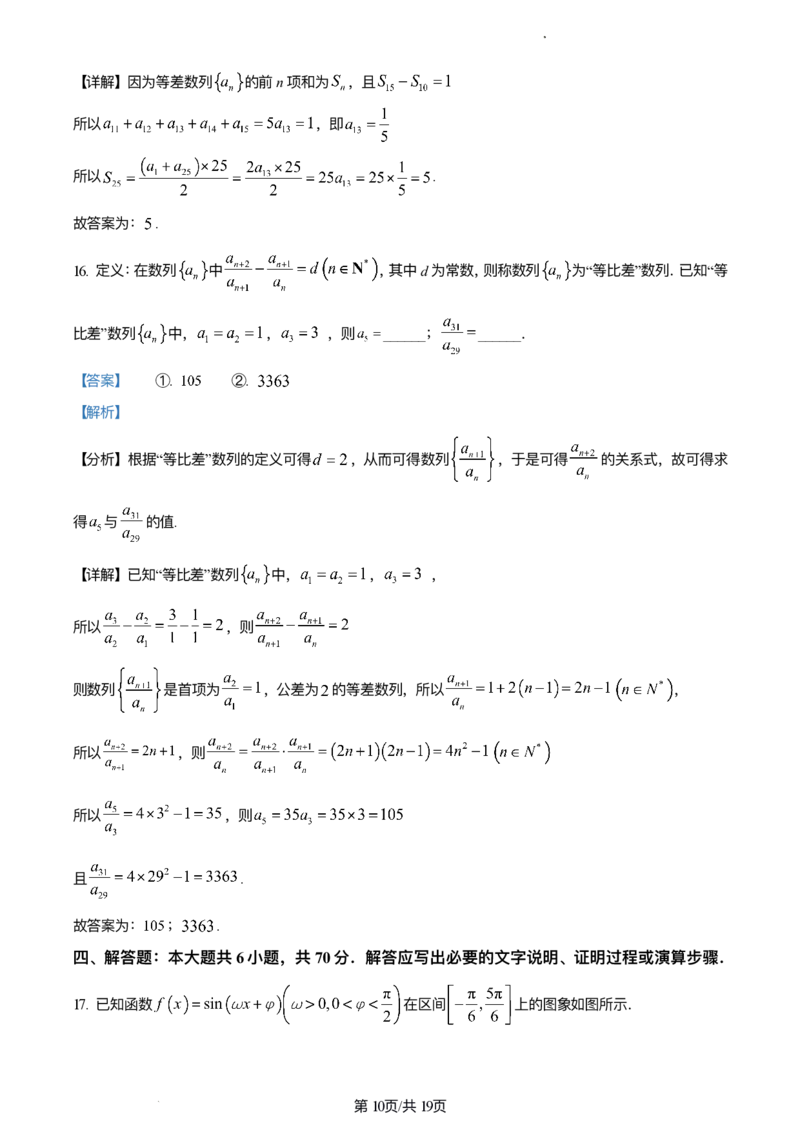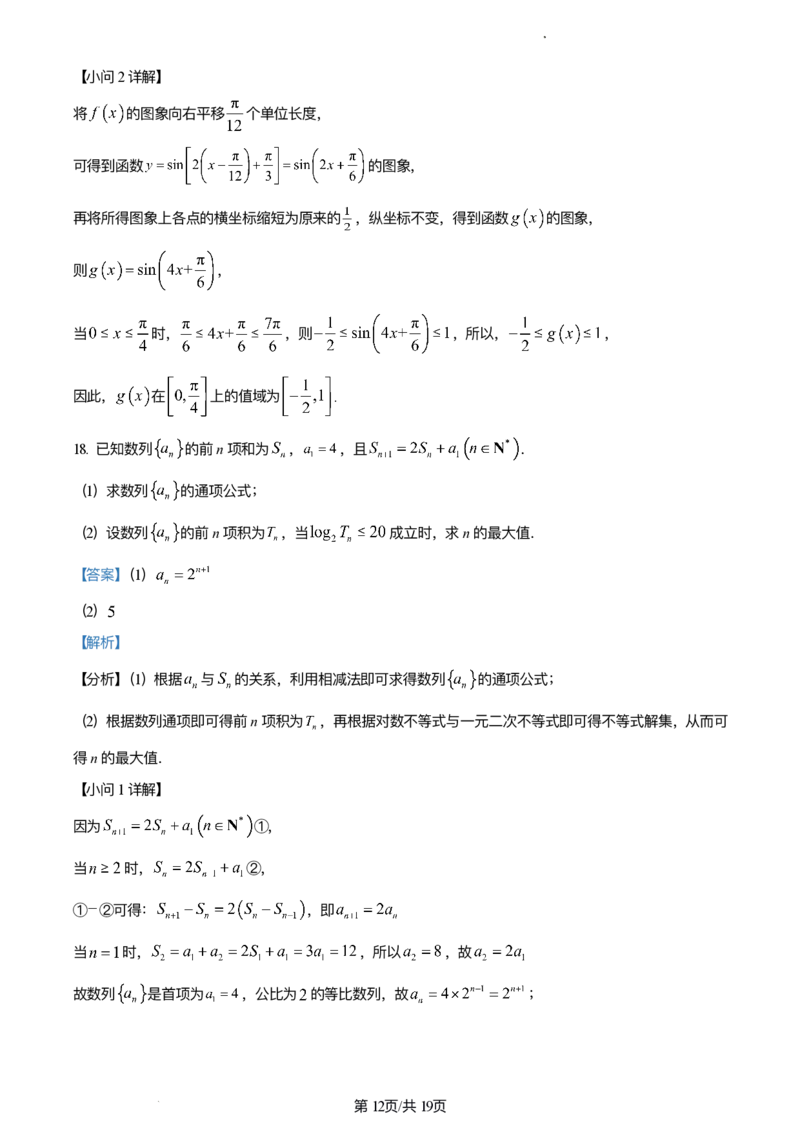文档内容
重庆育才中学 ⻄南⼤学附中
⾼ 2024 届拔尖强基联盟⾼三⼗⽉联合考试
数学试题
(满分:150分;考试时间:120分钟)
命题学校:重庆育才中学
2023年10⽉
注意事项:
1.答题前,考⽣先将⾃⼰的地名、班级、考场/座位号、准考证号填写在答题卡上.
2.答选择题时,必须使⽤2B铅笔填涂;答⾮选题题时,必须使⽤ 0.5毫⽶的⿊⾊签字笔书写;
必须在题号对应的答题区域内作答,超出答题区域书写⽆效;保持答卷清洁、完整.
3.考试结束后,将答题卡交回(试题卷学⽣留存,以备评讲).
⼀.单选题:本⼤题共8⼩题,每⼩题5分,共40分.在每⼩题给出的四个选项中,只有⼀项
是符合题⽬要求的.
1. 复数 (i为虚数单位)复平⾯内对应的点位于( )
A. 第⼀象限 B. 第⼆象限 C. 第三象限 D. 第四象限
【答案】D
【解析】
【分析】判断复数在复平⾯上的象限,只要把复数表示成标准的复数形式即可.
【详解】 ,所以复数在复平⾯内对应的点为(2,-3),位于第四象限.
故选:D
2. 设集合 , ,则 ( )
A. B. C. D.
【答案】A
【解析】
【分析】先化简集合A,B,再根据补集和交集的概念即可求解.
【详解】由 ,得 , , ,
,
第1⻚/共19⻚
学科⽹(北京)股份有限公司故选:A
3. 已知数列 满⾜ ,若 ,则 ( )
A. B. C.12 D.36
【答案】D
【解析】
【分析】由 可知数列 是公⽐为 的等⽐数列,再由题意结合等⽐数列的通项公式代⼊可
求出答案.
【详解】由 可知数列 是公⽐为 的等⽐数列,
所以 ,
解得: .
故选:D.
4. 已知向量 , ,若 ,则 ( )
A.-6 B.0 C. D.
【答案】C
【解析】
【分析】根据向量共线的坐标表示列出⽅程求参,再结合向量的数量积的运算公式,即可求解.
【详解】由向量 ,
因为 ,所以
所以 .
故选:C.
5. 在 中,⻆A,B,C所对的边分别是a,b,c,则“ ”是 为直⻆三⻆
形的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分⼜不必要条件
【答案】D
【解析】
第2⻚/共19⻚
学科⽹(北京)股份有限公司【分析】由 ,利⽤正弦定理得到 ,再利⽤三
⻆恒等变换得到 求解.
【详解】解:因为 ,
所以 ,
则 ,
则 ,
化简得 ,
所以 或 ,
所以 或 ,
所以 为直⻆三⻆形( )或等腰三⻆形,
所以“ ”是 为直⻆三⻆形的既不充分⼜不必要条件.
故选:D
6. 已知函数 在 上单调递增,则实数m的最⼤值为( )
A. B. C. D.
【答案】A
【解析】
【分析】根据正弦型函数的单调性列不等式组解得实数m的取值范围,即可得实数m的最⼤值.
【详解】因为 ,则 ,所以 ,
⼜函数 在 上单调递增,
所以
则 ,⼜
第3⻚/共19⻚
学科⽹(北京)股份有限公司故 ,所以实数m的最⼤值为 .
故选:A.
7. 新⻛机的⼯作原理是,从室外吸⼊空⽓,净化后输⼊室内,同时将等体积的室内空⽓排向室外.假设某
房间的体积为 ,初始时刻室内空⽓中含有颗粒物的质量为m.已知某款新⻛机⼯作时,单位时间内从室
外吸⼊的空⽓体积为(v ),室内空⽓中颗粒物的浓度与时刻t的函数关系为 ,
其中常数 为过滤效率.若该款新⻛机的过滤效率为 ,且 时室内空⽓中颗粒物的浓度是 时的
倍,则v的值约为( )
(参考数据: , )
A.1.3862 B.1.7917 C.2.1972 D.3.5834
【答案】B
【解析】
【分析】由题意表达出 ,由 列出⽅程,求出 ,两边取对数,计算出答案.
【详解】由题意得 , ,
因为 ,所以 ,
整理得 ,
令 ,
因为 ,所以 ,
则 ,解得 (舍去)或 ,
故 ,解得 .
故选:B
8. 已知⻆ , 均在 内, , ,则⻆ 的值为( )
A. B. C. D.
【答案】C
第4⻚/共19⻚
学科⽹(北京)股份有限公司【解析】
【分析】根据题意,由同⻆的平⽅关系可得 ,再由余弦的和差⻆公式,即可得到结果.
【详解】因为 ,且 ,所以 ,
因为 ,所以 ,所以 为钝⻆,
所以 ,
则
,且 ,则 .
故选:C
⼆.多选题:本⼤题共 4⼩题,每⼩题5分,共20分.在每⼩题给出的四个选项中,有多项是
符合题⽬要求的,全部选对得5分,部分选对的得2分,有选错的得 0分.
9. 关于平⾯向量,有下列四个命题,其中说法正确的是( )
A. 向量 , 能作为平⾯内所有向量的⼀组基底
B. 若点G是 的重⼼,则
C. 若 ,则 或
D. 若向量 , ,则向量 在向量 上的投影向量为
【答案】BD
【解析】
【分析】由基底的概念即可判断A,由三⻆形重⼼的定义即可判断B,由平⾯向量数量积的定义即可判断C,
由投影向量的概念即可判断D.
【详解】因为向量 , ,则 ,即 ,则 不能作为平⾯内 基底,故
A错误;
第5⻚/共19⻚
学科⽹(北京)股份有限公司如图所示,连接 并延⻓交 于 点,点 为 中点,延⻓ 到点 ,使得 ,则
, ,所以 ,故B正确;
因为 ,若 ,则 或 或 ,故C错误;
因为向量 , ,则向量 在向量 上的投影向量为
,故D正确;
故选:BD
10. 设函数 ,则下列结论正确的是( )
A. 的最⼩正周期为 B. 的图象关于直线 对称
C. 的⼀个零点为 D. 的最⼤值为1
【答案】ABD
【解析】
【分析】根据辅助⻆公式化简函数,再结合三⻆函数图象相关知识逐⼀判断即可.
【详解】函数 .
对于A, 的最⼩正周期为 ,故A正确;
对于B, ,所以 的图象关于直线 对称,故B正确;
对于C, ,所以 不是 的⼀个零点,故C错误;
对于D,函数 ,则 的最⼤值为1,故D正确.
第6⻚/共19⻚
学科⽹(北京)股份有限公司故选:ABD.
11. 以下说法错误的是( )
..
A. 若 的定义域为 ,则 的定义域为
B. 若 在 上的值域 ,则 在 上的值域也为
C. 若 为R上的奇函数,则 也为R上的奇函数
D. 若 是R上的单调递增函数,则 是 的单调递减函数
【答案】AB
【解析】
【分析】根据函数的概念与性质⼀⼀判定即可.
【详解】对于A项,若 的定义域为 ,则要求 的定义域,
需 ,故A错误;
对于B项, 若 在 上的值域 ,⽽ 时, ,
所以 在 上的值域为函数 在 上的值域,不⼀定为 ,
故B错误;
对于C项,设 ,
若 为R上的奇函数,则 , 所以
,
故 也为R上的奇函数,C正确;
对于D项,由复合函数的单调性可知 在定义域 上单调递减,
⽽ 是单调递增函数,故 是 的单调递减函数,即D正确.
故选:AB.
12. 在三⻆形ABC中,点D⾜AB边上的四等分点且 ,AC边上存在点E满⾜ ,
直线CD和直线BE交于点F,若 ,则( )
第7⻚/共19⻚
学科⽹(北京)股份有限公司A. B.
C. 的最⼩值为17 D.
【答案】ABD
【解析】
【分析】根据平⾯向量的线性运算、共线定理、数量积的运算性质逐项判断即可.
【详解】因为 ,所以 ,
所以 ,故A正确;
⼜因为 ,则 ,
因为 ,所以
⼜
三点共线,所以 ,整理得 ,故B正确;
由 可得 ,所以 ,因为 ,当 时,
,故 的最⼩值不为 ,故C不正确;
由于 ,所以 ,则 ,
所以 ⼜
,当且仅当 时,等号成⽴
第8⻚/共19⻚
学科⽹(北京)股份有限公司所以 的最⼤值为 ,故D正确.
故选:ABD.
三、填空题:本⼤题共4⼩题,每⼩题5分,共 20分.
13. 已知向量 , 的夹⻆为 ,且 , ,则 等于______.
【答案】1
【解析】
【分析】根据数量积的定义求解 ,再根据数量积的应⽤与运算律求解 的值即可.
【详解】因为向量 , 的夹⻆为 ,且 ,
所以 ,
则 .
故答案为: .
14. 写出⼀个同时具有下列两个性质的函数 :______.
① 的值域为 ;②当 时, .
【答案】
【解析】
【分析】根据题意,考虑指数型函数,即可得到结果.
【详解】由题意可得,函数 在 上单调递增,且最⼩值为 ,
由指数函数 在 上单调递增且 ,
将其向上平移2个单位可得 ,符合题意.
故答案为:
15. 已知等差数列 的前n项和为 ,若 ,则 ______.
【答案】5
【解析】
【分析】根据等差数列的性质与前n项和的公式转化求解即可得 的值.
第9⻚/共19⻚
学科⽹(北京)股份有限公司【详解】因为等差数列 的前n项和为 ,且
所以 ,即
所以 .
故答案为: .
16. 定义:在数列 中 ,其中d为常数,则称数列 为“等⽐差”数列.已知“等
⽐差”数列 中, , ,则 ______; ______.
【答案】 ①. ②.
【解析】
【分析】根据“等⽐差”数列的定义可得 ,从⽽可得数列 ,于是可得 的关系式,故可得求
得 与 的值.
【详解】已知“等⽐差”数列 中, , ,
所以 ,则
则数列 是⾸项为 ,公差为 的等差数列,所以 ,
所以 ,则
所以 ,则
且 .
故答案为: ; .
四、解答题:本⼤题共6⼩题,共70分.解答应写出必要的⽂字说明、证明过程或演算步骤.
17. 已知函数 在区间 上的图象如图所示.
第10⻚/共19⻚
学科⽹(北京)股份有限公司(1)求函数 的解析式;
(2)将函数 的图象向右平移 个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐
标不变,得到函数 的图象,求函数 在 上的值域.
【答案】(1) ;
(2)
【解析】
【分析】(1)由图象可得出函数 的最⼩正周期,可求得 的值,由 结合 的取值范围可求
出 的值,由此可得出函数 的解析式;
(2)利⽤三⻆函数图象变换可得出函数 的解析式,利⽤正弦型函数的基本性质可求得函数 在
上的值域.
【⼩问1详解】
由图象可知,函数 的最⼩正周期为 ,则 ,
所以, ,
因为 ,
因为 ,则 ,所以, ,解得 ,
因此, .
第11⻚/共19⻚
学科⽹(北京)股份有限公司【⼩问2详解】
将 的图象向右平移 个单位⻓度,
可得到函数 的图象,
再将所得图象上各点的横坐标缩短为原来的 ,纵坐标不变,得到函数 的图象,
则 ,
当 时, ,则 ,所以, ,
因此, 在 上的值域为 .
18. 已知数列 的前n项和为 , ,且 .
(1)求数列 的通项公式;
(2)设数列 的前n项积为 ,当 成⽴时,求n的最⼤值.
【答案】(1)
(2)
【解析】
【分析】(1)根据 与 的关系,利⽤相减法即可求得数列 的通项公式;
(2)根据数列通项即可得前n项积为 ,再根据对数不等式与⼀元⼆次不等式即可得不等式解集,从⽽可
得n的最⼤值.
【⼩问1详解】
因为 ①,
当 时, ②,
① ②可得: ,即
当 时, ,所以 ,故
故数列 是⾸项为 ,公⽐为 的等⽐数列,故 ;
第12⻚/共19⻚
学科⽹(北京)股份有限公司【⼩问2详解】
数列 的前n项积为
则不等式 为 ,所以 ,即
解得 ,所以n的最⼤值为 .
19. 太阳能热⽔器因节能环保⽽深受⼴⼤消费者的⻘睐,但它也有缺点——持续阴天或⾬天便⽆法正常使⽤.
为解决这⼀缺陷,现在的太阳能热⽔器⽔箱上都安装了辅助电加热器,如果天⽓不好或冬季⽔温⽆法满⾜需
要时,就可以通过辅助电加热器把⽔温升⾼,⽅便⽤户使⽤.某⼯⼚响应“节能减排”的号召,决定把原来给
锅炉加热的电热⽔器更换成电辅式太阳能热⽔器.电铺式太阳能热⽔器的耗电情况受当天的⽇照时⻓和⽇
均⽓温影响,假设每天的⽇照情况和⽇均⽓温相互独⽴,该电辅式太阳能热⽔器每⽇耗电情况如下表所示:
⽇照情况 ⽇均⽓温不低于15℃ ⽇均⽓温低于15℃
⽇照充⾜ 耗电0千瓦时 耗电5千瓦时
⽇照不⾜ 耗电5千瓦时 耗电10千瓦时
⽇照严重不⾜ 耗电15千瓦时 耗电20千瓦时
根据调查,当地每天⽇照充⾜的概率为 ,⽇照不⾜的概率为 ,⽇照严重不⾜的概率为 .2023年这⼀
年的⽇均⽓温的频率分布直⽅图如图所示,区间分组为 , , , , ,
.
(1)求图中a的值,并求⼀年中⽇均⽓温不低于15℃的频率;
(2)⽤频率估计概率,已知该⼯⼚原来 电热⽔器平均每天耗电20千瓦时,试估计更换电辅式太阳能热⽔
器后,每天能省多少电?
【答案】(1) , ;
(2) 千瓦时.
【解析】
第13⻚/共19⻚
学科⽹(北京)股份有限公司【分析】(1)根据频率分布直⽅图中频率和为1求出区间 的频率,再除以组距求得 的值,再利⽤
⻓⽅形⾯积等于频率,求出不低于15℃的频率;
(2)由(1)知⼀年中⽇均⽓温不低于15℃的概率的估计值为 ,低于15℃的概率的估计值为 ,分析题
意可知,使⽤电辅式太阳能热⽔器⽇均耗电量 的可能取值为0,5,10,15,20,分别算出事件对应的概率,
写出分布列,即可得出期望,即可得到使⽤电辅式太阳能热⽔器⼀天节省的电量.
【⼩问1详解】
依题意得 .
⼀年中⽇均⽓温不低于15℃ 频率为 .
【⼩问2详解】
这⼀年中⽇均⽓温不低于15℃的概率的估计值为 ,⼀年中⽇均⽓温低于15℃的概率的估计值为 ,
设使⽤电辅式太阳能热⽔器⽇均耗电量为 , 的所有可能取值为0,5,10,15,20
, , ,
, .
所以 的分布列为
0 5 10 15 20
所以 的数学期望
所以使⽤电辅式太阳能热⽔器⼀天节省的电量为 (千瓦时).
20. 如图,在 中,点 在边 上, , , .
(1)求证: ;
第14⻚/共19⻚
学科⽹(北京)股份有限公司(2)若 ,求 .
【答案】(1)证明⻅解析
(2)
【解析】
【分析】(1)由正弦定理得到 ,再由锐⻆三⻆函数得到 ,
最后由诱导公式计算可得;
(2)设 ,根据平⾯向量的线性运算得到 ,再根据数量积的运算律及定义得到⽅
程求出 ,最后由⾯积公式计算可得.
【⼩问1详解】
在 中, ,
由正弦定理可得 ,
所以 ,
在 中, .
则 ,由于 , ,
所以 ,
即 .
【⼩问2详解】
在 中,设 则 ,
∵ ,∴ ,
所以 ,
所以 ,解得 或 (舍去),
∴ .
第15⻚/共19⻚
学科⽹(北京)股份有限公司21. 已知函数 ,函数 与 关于点 中⼼对称.
(1)求 的解析式;
(2)若⽅程 有两个不等 实根 , ,且 ,求a的值.
【答案】(1)
(2)
【解析】
【分析】(1)根据函数的对称性可得 ,从⽽可得 的解析式;
(2)根据⽅程的根,利⽤⼀元⼆次⽅程根与系数的关系与指数函数的性质,结合 ,即可求得a
的值.
【⼩问1详解】
已知函数 ,函数 与 关于点 中⼼对称
所以 ,则
【⼩问2详解】
由于⽅程 有两个不等的实根 , ,不妨设
即 两个不等的实根,则 ,由于函数 是递增函数,
所以 ①, ②
因为 , ,则 ,
所以 ,则 代⼊②得: ,解得 ,
代⼊①得 .
22. 已知 .
(1)若对 ,都有 恒成⽴,求 的取值范围;
第16⻚/共19⻚
学科⽹(北京)股份有限公司(2)当 时, 在 上的最⼤值为 ,求 的值域.
【答案】(1)
(2)
【解析】
【分析】(1)根据单调性定义可知 在 上单调递增,得到 ,采⽤分离变量法和换元法可得
在 上恒成⽴,根据⼆次函数的最值可求得 的取值范围;
(2)求导后,采⽤换元法,结合⼆次函数的零点可求得 在 上的单调性,并确定最⼤值点
的取值范围,结合单调性可得 ,进⽽⽤ 表示出 的取值范围;利⽤导数可分别求得 最⼤
值和最⼩值的取值范围,从⽽最终确定所求值域.
【⼩问1详解】
对 ,都有 恒成⽴, 在 上单调递增,
在 上恒成⽴,
,
令 ,则 在 上恒成⽴,
为开⼝⽅向向上,对称轴为 的抛物线,
当 时, , ,
即实数 的取值范围为 .
【⼩问2详解】
,
当 时, ,
令 , ,
为开⼝⽅向向下,对称轴为 的抛物线,
第17⻚/共19⻚
学科⽹(北京)股份有限公司在 上单调递减, ,
当 时, , ,
令 ,解得: (舍)或 ;
当 时, ;当 时, ;
⼜ 在 上单调递增,记 , ,
当 时, ;当 时, ;
在 上单调递增,在 上单调递减,
,即 ,
当 时, ,即 , ;
上单调递增, ;
令 , ,则 ,
,
在 上单调递减, ;
令 , ,则 ,
,
在 上单调递增, ;
第18⻚/共19⻚
学科⽹(北京)股份有限公司.
【点睛】关键点点睛:本题考查根据函数单调性求解参数范围、利⽤导数求解恒成⽴问题;本题求解的关键
是能够结合三⻆恒等变换的知识,采⽤换元法来对导函数的零点进⾏求解,从⽽确定原函数的单调性和最值
点.
第19⻚/共19⻚
学科⽹(北京)股份有限公司