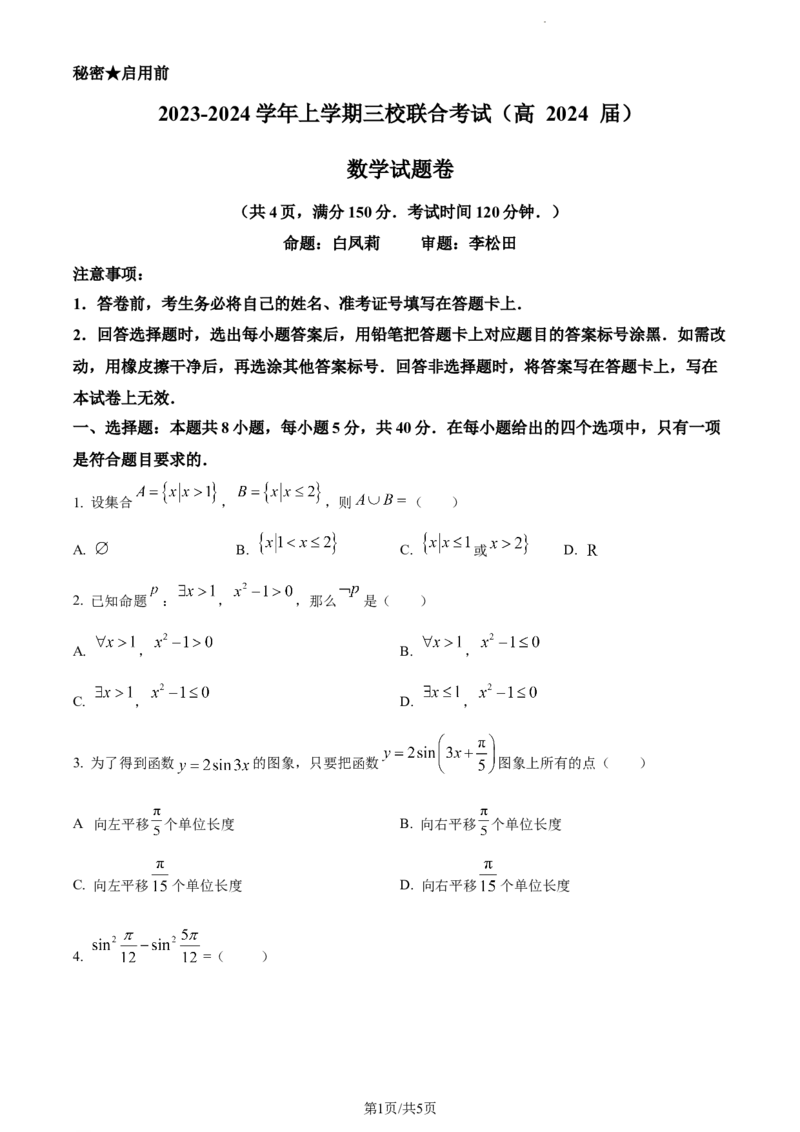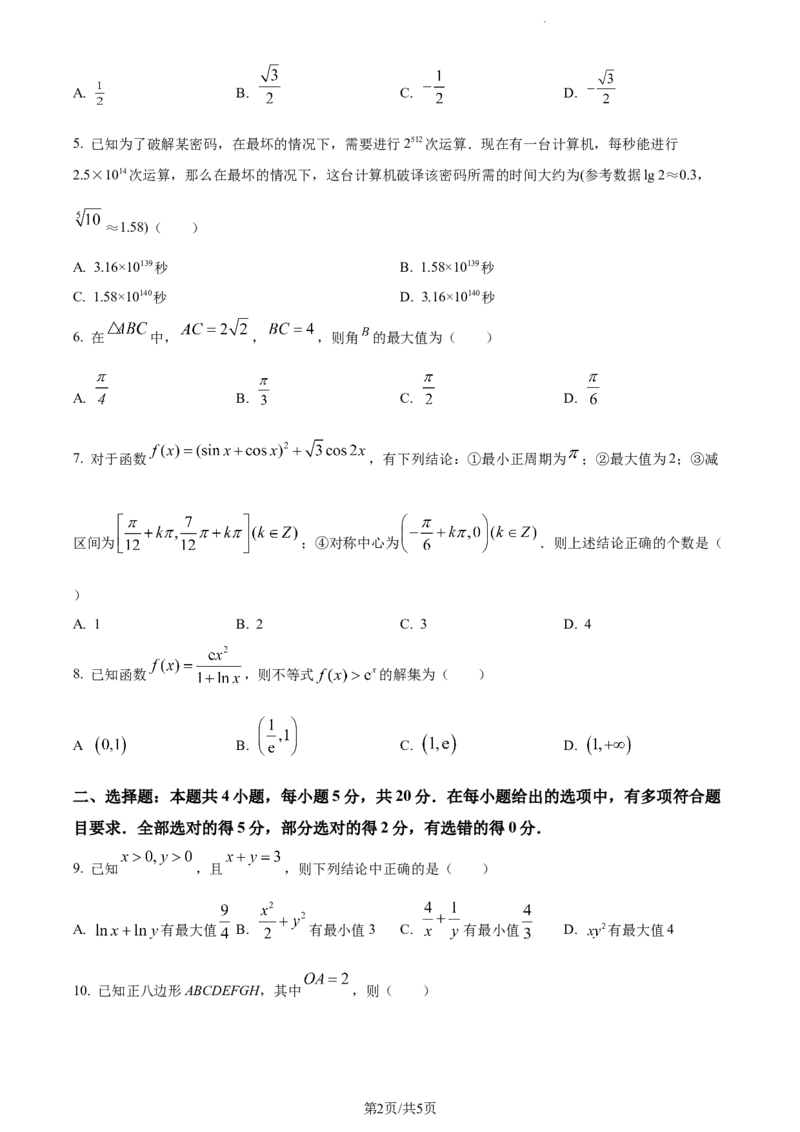文档内容
秘密★启用前
2023-2024 学年上学期三校联合考试(高 2024 届)
数学试题卷
(共4页,满分150分.考试时间120分钟.)
命题:白凤莉 审题:李松田
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改
动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在
本试卷上无效.
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项
是符合题目要求的.
1. 设集合 , ,则 ( )
A. B. C. 或 D.
2. 已知命题 : , ,那么 是( )
A. , B. ,
C. , D. ,
3. 为了得到函数 的图象,只要把函数 图象上所有的点( )
.
A 向左平移 个单位长度 B. 向右平移 个单位长度
C. 向左平移 个单位长度 D. 向右平移 个单位长度
4. =( )
第1页/共5页
学科网(北京)股份有限公司A. B. C. D.
5. 已知为了破解某密码,在最坏的情况下,需要进行2512次运算.现在有一台计算机,每秒能进行
2.5×1014次运算,那么在最坏的情况下,这台计算机破译该密码所需的时间大约为(参考数据lg 2≈0.3,
≈1.58)( )
A. 3.16×10139秒 B. 1.58×10139秒
C. 1.58×10140秒 D. 3.16×10140秒
6. 在 中, , ,则角 的最大值为( )
A. B. C. D.
7. 对于函数 ,有下列结论:①最小正周期为 ;②最大值为2;③减
区间为 ;④对称中心为 .则上述结论正确的个数是(
)
A. 1 B. 2 C. 3 D. 4
8. 已知函数 ,则不等式 的解集为( )
.
A B. C. D.
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题
目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.
9. 已知 ,且 ,则下列结论中正确的是( )
A. 有最大值 B. 有最小值3 C. 有最小值 D. 有最大值4
10. 已知正八边形ABCDEFGH,其中 ,则( )
第2页/共5页
学科网(北京)股份有限公司A. B.
C. D.
11. 已知定义在 上 的偶函数 ,满足 ,则下列结论正确的是( )
A. 的图象关于 对称
B.
C. 若函数 在区间 上单调递增,则 在区间 上单调递增
D. 若函数 在区间 上 的解析式为 ,则 在区间 上的解析式为
12. 已知函数 及其导函数 满足 ,且 ,则( )
A. 在 上单调递增 B. 在 上有极小值
C. 的最小值为-1 D. 的最小值为0
三、填空题:本题共4小题,每小题5分,共20分.
13. 设 则 是 成立的___________条件.(填“充分不必要”、“必要不充分”、
“充要”或“既不充分也不必要”)
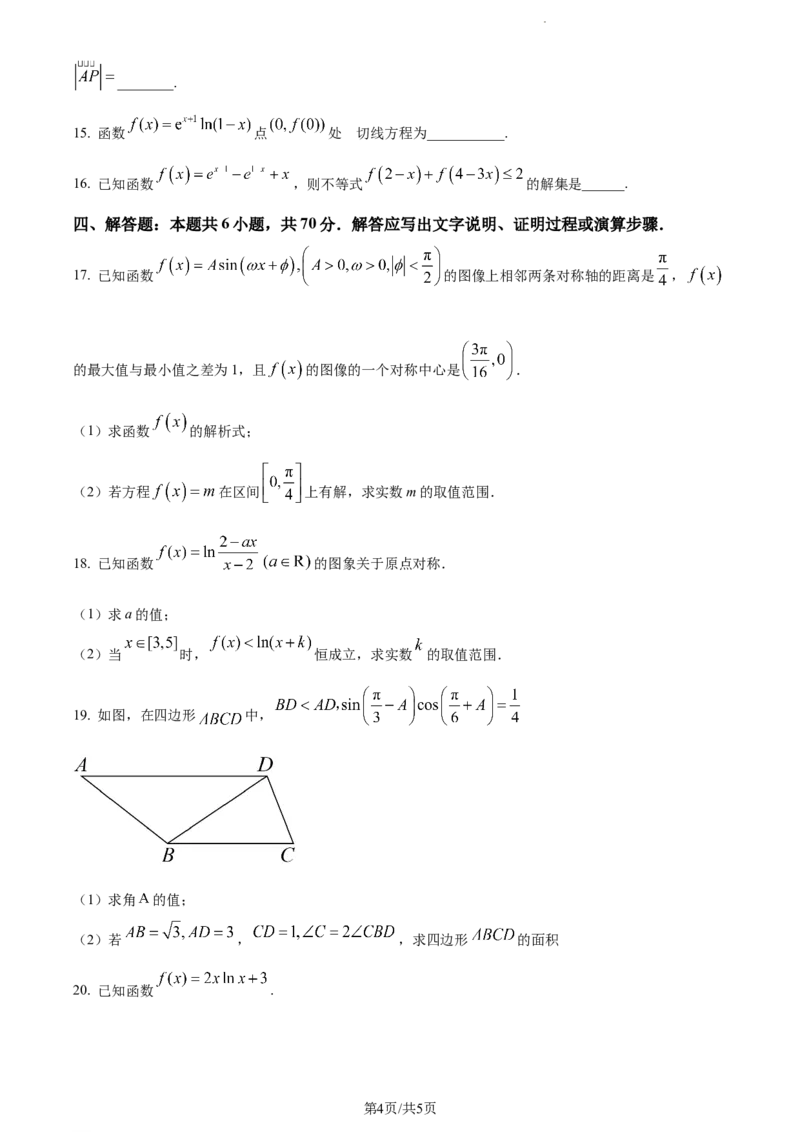
14. 在边长为 的等边 中,已知 ,点 在线段 上,且 ,则
第3页/共5页
学科网(北京)股份有限公司________.
的
15. 函数 点 处 切线方程为___________.
16. 已知函数 ,则不等式 的解集是______.
四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17. 已知函数 的图像上相邻两条对称轴的距离是 ,
的最大值与最小值之差为1,且 的图像的一个对称中心是 .
(1)求函数 的解析式;
(2)若方程 在区间 上有解,求实数m的取值范围.
18. 已知函数 的图象关于原点对称.
(1)求a的值;
(2)当 时, 恒成立,求实数 的取值范围.
19. 如图,在四边形 中,
(1)求角 的值;
(2)若 , ,求四边形 的面积
20. 已知函数 .
第4页/共5页
学科网(北京)股份有限公司(1)求 的单调区间;
(2)求 过点 的切线方程.
21. 在 中,角 , , 所对的边分别为 , , , .
(1)求角 的大小;
(2)若 是锐角三角形,且其面积为 ,求边 的取值范围.
22. 已知函数 , .
(1)讨论 的单调性并求极值.
(2)设函数 ( 为 的导函数),若函数 在 内有两个不同的零
点,求实数 的取值范围.
第5页/共5页
学科网(北京)股份有限公司