文档内容
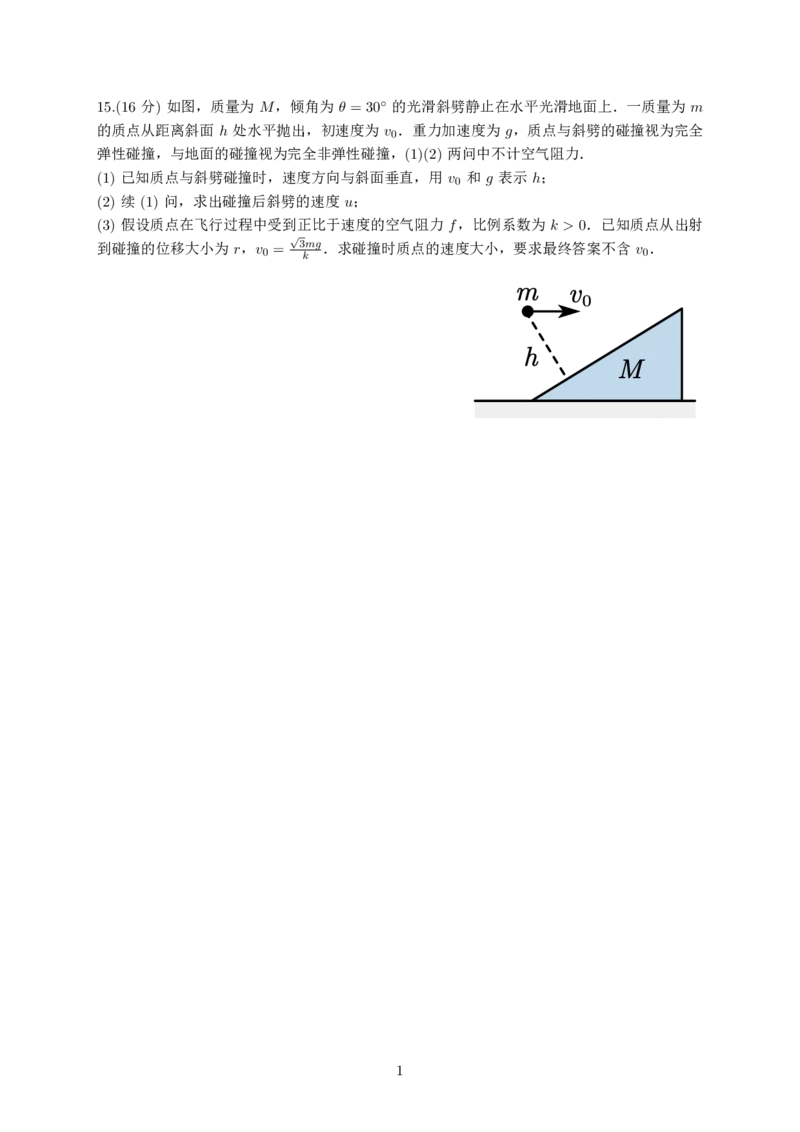
15.(16 分) 如图,质量为 M,倾角为 θ = 30 ◦ 的光滑斜劈静止在水平光滑地面上.一质量为 m
的质点从距离斜面 h 处水平抛出,初速度为 v .重力加速度为 g,质点与斜劈的碰撞视为完全
0
弹性碰撞,与地面的碰撞视为完全非弹性碰撞,(1)(2) 两问中不计空气阻力.
(1) 已知质点与斜劈碰撞时,速度方向与斜面垂直,用 v 和 g 表示 h;
0
(2) 续 (1) 问,求出碰撞后斜劈的速度 u;
(3) 假设质点在飞行过程中受到正比于速度的空气阻力 f,比例系数为 k > 0.已知质点从出射
√
到碰撞的位移大小为 r,v = 3mg.求碰撞时质点的速度大小,要求最终答案不含 v .
0 k 0
115. 解 (1) 如图,将速度按平行于斜面和垂直于斜面正交分解
质点在 x 和 y 方向上均做匀变速直线运动,出射到碰撞经过的时间为
v cosθ
0
t = . (1)
1
gsinθ
可得 y 方向位移大小
1
h = v t sinθ+ gcosθt2. (2)
0 1 2 1
带入 θ = 30 ◦ 整理得到 √
5 3v2
h = 0. (3)
4 g
(2) 由几何关系得,碰撞前质点的速度为
v = 2v . (4)
1 0
将碰撞分为两个阶段,先看质点和斜劈的碰撞. 由于斜面光滑,碰后质点的速度仍垂直于斜面,
设为 v ,斜劈速度与 v 反向,设为 u ,由动量和能量守恒
2 2 1
mv = Mu −mv ,
1 1 2
(5)
1mv2 = 1mv2+ 1Mu2.
2 1 2 2 2 1
有意义的解为
4m
u = v . (6)
1 0
M +m
下面考虑斜劈和地面的碰撞. 由于地面光滑,且碰撞是非弹性的,故
2m
u = u sinθ = v . (7)
1 0
M +m
(3) 注意到
kv sinθ = mgcosθ. (8)
0
因而 y 方向上的运动为匀速直线运动,出射到碰撞经过的时间为
h 2kh
t = = √ . (9)
v 0 sinθ 3mg
用配速法也能得到类似的结论.另一方面,在 x 方向上使用动量定理得
m(v −v cosθ) = −mgsinθt−kx. (10)
x 0
2由几何关系
√
x = r2−h2. (11)
代入得
√
3mg kh k
v = − √ − r2−h2. (12)
x
2 k 3m m
最终有 √
√ ( 3mg kh k √ ) 2 3m2g2
v = v2 +v2 = − √ − r2−h2 + . (13)
x y 2 k 3m m 4 k2
评分细则:(1)(2) 各 1 分;(3)2 分;(4)1 分,(5)(6) 各 2 分,(7)1 分;(8)2 分;(10)(11)(12)(13)
各 1 分
3